课程： 5.3 牛顿世界重力法

章节大纲

选择节常规

折叠展开
常规

全部折叠展开全部
- 选择活动新闻通告
  
  新闻通告讨论区

牛顿的万国引力法

What if I told you that right now, you’re pulling the Earth toward you? It’s true! Every object with mass—even you—exerts a gravitational force on everything else. The Earth is pulling you back with the exact same force, but because the Earth is so massive, its is so small you’d never notice it. This invisible connection is what Isaac Newton captured in his Universal Law of Gravitation, explaining falling apples, orbiting planets, and even you with the rest of the universe.
::如果我现在告诉你,你正在把地球拉向你呢?这是真的!每个物体,即使你也是如此,都对其它物体施加了引力。地球正用同样的力把你拉回来,但因为地球如此巨大,所以你从未注意到它如此之小。这种无形的联系就是艾萨克·牛顿在他的《万国引力法》中所捕捉的,解释苹果落下、行星运行、甚至你与宇宙其他部分的关系。

Force of Gravity
::重力力

Legend has it that Isaac Newton began pondering this universal force when he saw an apple fall from a tree. Realizing that the same force pulling the apple downward also pulls the Moon towards Earth, and even keeps planets orbiting the Sun, Figure (below). He proposed a formula to describe this force:
::传说伊萨克·牛顿在看到苹果从树上掉下来时开始思考这一全球力量。他意识到拉苹果的同一力量也把月球拉向地球,甚至把绕太阳运行的行星都固定在图中(下面)。他提出了一个描述这一力量的公式:

\begin{aligned} F = \frac{G m_{1} m_{2}}{r^{2}} \end{aligned}

Where:
::F=Gm1m2r2,其中:

$\begin{aligned} F \end{aligned}$ is the gravitational force,
::F是引力力力,

$\begin{aligned} G \end{aligned}$ is the universal gravitational constant $\begin{aligned} (6.67 \times 10^{- 11} N \cdot m^{2} / {kg}^{2}), \end{aligned}$
::G是普遍引力常数(6.67×10-11 Nm2/kg2),

::G是普遍引力常数(6.67×10-11 Nm2/kg2),

$\begin{aligned} m_{1} \end{aligned}$ and $\begin{aligned} m_{2} \end{aligned}$ are the masses involved,
::m1 和 m2 涉及的群众,

::m1 和 m2 涉及的群众,

$\begin{aligned} r \end{aligned}$ is the between the centers of the masses.
::r 是大众中间的中心。

::r 是大众中间的中心。

This equation explains why Earth pulls objects to its surface and why you exert a tiny gravitational pull on your friend across the room (yes, this really is happening!).
::这个方程式解释了为什么地球将物体拉向它的表面, 也解释了为什么你对房间对面的朋友施加微小的引力拉动(是的,这是真的发生! ) 。

While Newton gave us the equation for gravity, one crucial piece was missing: the value of $\begin{aligned} G . \end{aligned}$
::当牛顿给了我们重力的方程式时, 缺少了一个关键部分:G值。

Discovering the gravitational constant
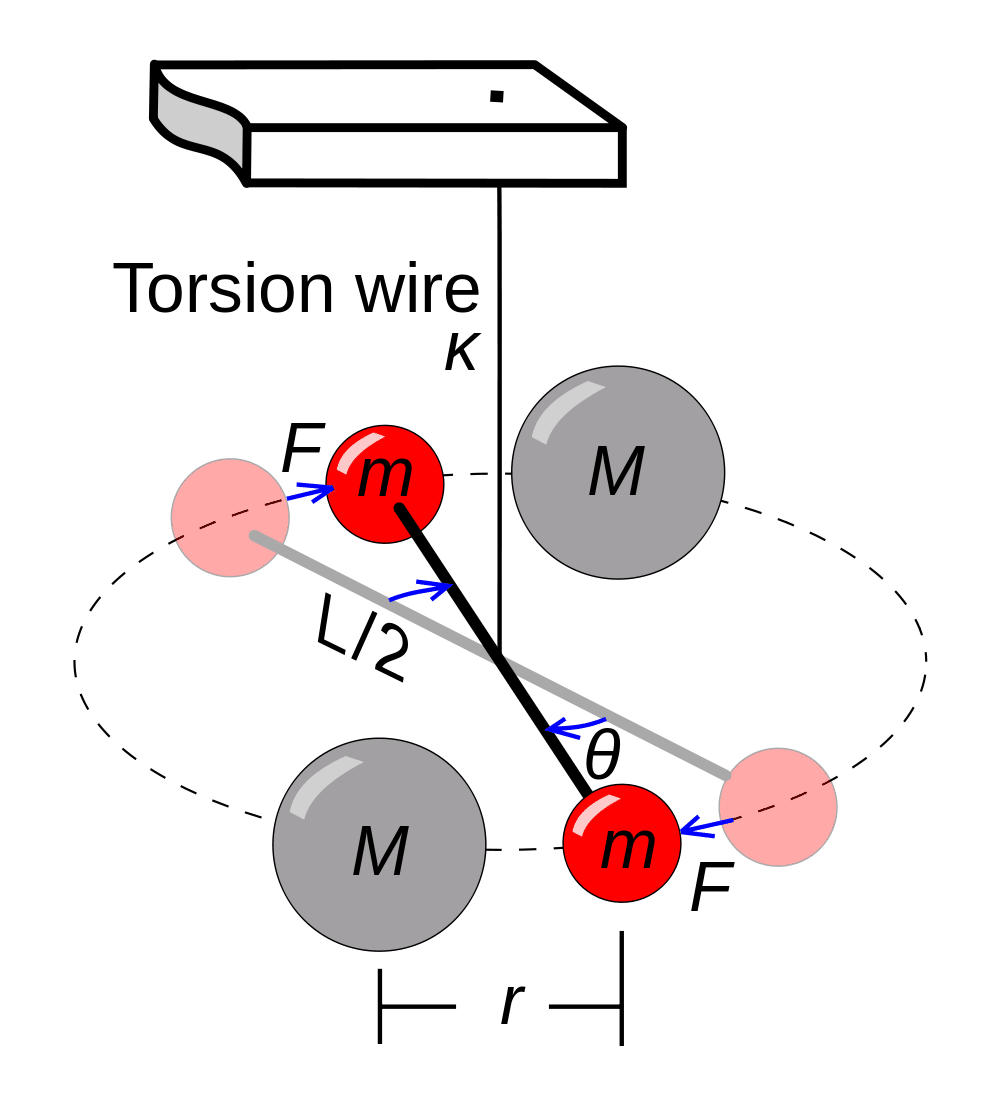
::发现引力常数

In 1798, Henry Cavendish designed an experiment to calculate $\begin{aligned} G . \end{aligned}$ Using a delicate apparatus shown in the Figure , with small lead spheres, he measured the tiny gravitational pull between them. From his work, we know $\begin{aligned} G \end{aligned}$ is approximately $\begin{aligned} 6.67 \times 10^{- 11} N \cdot m^{2} / {kg}^{2} \end{aligned}$ , unlocking the ability to calculate gravitational forces everywhere in the universe.
::1798年,亨利·卡文迪什设计了一个用来计算G的实验。他用图中显示的精密仪器,用很小的铅球测量了它们之间的微小引力拉动。从他的工作来看,我们知道G大约是6.67×10-11Nm2/kg2,这释放了计算宇宙各地引力力的能力。

Diagram of Cavendish torsion balance measuring the gravitational force between masses to determine the gravitational constant G. — This is a torsion balance used in Henry Cavendish’s experiment to measure the gravitational constant (G) by observing the force between lead masses.

Calculating Earth's Mass
::计算地球质量

Now we know the value of G, we can use Newton’s formula to calculate Earth’s mass. We know that the gravity on a 1.00 kg object is 9.81 N and Earth’s radius is 6,380 km.
::现在我们知道G值,我们可以使用牛顿的公式来计算地球质量。我们知道1千克物体的重力是9.81N,地球半径是6,380公里。

In 1798, Henry Cavendish designed and created an apparatus and experiment to determine the density of the planet and the value of the gravitational constant, $\begin{aligned} G \end{aligned}$ . His apparatus involved a light, rigid rod about 2-feet long with two small lead spheres attached to the ends. The rod was suspended by a thin wire. When the rod rotated, the twisting of the wire pushed backwards to restore the rod to the original position.
::1798年,亨利·卡文迪什设计并创建了一个仪器和实验,以确定地球的密度和引力常数G.的值。他的仪器涉及一个大约两英尺长的硬杆,两英尺长,两小块铅球附在顶端。杆被一根细线悬吊。当杆旋转时,钢丝的扭动向向后推,使杆恢复原位置。

First, convert the radius into meters:
::首先,将半径转换成米:

Since $\begin{aligned} 1 km = 1, 000 m, \end{aligned}$ multiply by $\begin{aligned} 1, 000 \end{aligned}$ and convert kilometers to meters.

\begin{aligned} 6, 380 km \times 1, 000 m/km = 6, 380, 000 m \equiv 6.38 \times 10^{6} m \end{aligned}

Next, let’s rearrange the formula for the mass of Earth:

\begin{aligned} F = \frac{G m_{E}}{r_{E}^{2}} \times m_{o} \end{aligned}

\begin{aligned} m_{E} = \frac{F r^{2}}{G m_{o}} \end{aligned}

Then, substitute the values from the question:

\begin{aligned} m_{E} = \frac{(9.81 N) \times (6.38 \times 10^{6} m)^{2}}{(6.67 \times 10^{- 11} {Nm}^{2} {/kg}^{2}) \times (1.00 kg)} \end{aligned}

\begin{aligned} m_{E} \approx 5.98 \times 10^{24} kg \end{aligned}

::自1公里=1,000米,乘以1,000乘以1,000,并将公里转换为米。 6,380公里×1,000m/km=6,380,000m6.38×106m 下一步,让我们重新排列地球质量的公式:F=GmERE2xmo mE=Fr2Gmo 然后,将问题值: mE=(9.81 N)x(6.38x106m)2(6.67x10-11 Nm2/kg2)x(1.00公斤)mE=5.98x1024kn

DID YOU KNOW?

Even though Earth is accelerated toward the Sun by gravity, it doesn’t crash into it. Why? Because Earth’s is just right to keep it moving in a nearly circular orbit. This balance between gravitational pull and motion keeps the planets in their paths.

Use the simulation below to learn more about gravity and orbital motion:
::使用下面的模拟来了解更多关于重力和轨道运动的知识:

Gravity Near the Earth's Surface
::近地球表面的重力

Near the surface of a planet, such as Earth, the distance r in the gravitational formula closely matches the planet's radius, as the center of mass is usually located at the planet's core. This distance doesn’t vary much for small changes in height. For instance, Earth’s radius is roughly 6,380 km, while the heights we typically encounter in day-to-day life are only a few kilometers above the surface at most. As a result, r can be treated as a fixed value equal to Earth’s radius, making approximately constant near the surface. Figure {ref} shows an illustration of this.
::在地球等行星表面附近,引力公式中的距离 r 与行星半径非常接近,因为质量中心通常位于行星的核心。这种距离对于高度的微小变化来说没有多大差别。例如,地球的半径约为6,380公里,而我们通常在日常生活中遇到的高度最多仅比表面高出几公里。因此,r可以被视为与地球半径相等的固定值,在接近地表时大致保持恒定值。图{ref}说明了这一点。

So what does this mean for calculating the force of gravity near the Earth’s surface? We can use Newton’s Universal Law of Gravitation equation to calculate it. For any object at height above the Earth’s surface, $\begin{aligned} h, \end{aligned}$ and a mass of $\begin{aligned} m_{o}, \end{aligned}$ the force due to gravity, $\begin{aligned} F, \end{aligned}$ is:
::这对计算地球表面附近引力的威力意味着什么?我们可以使用牛顿的宇宙引力法方程式来计算。对于地球表面高处的物体,h和摩的重量,引力的威力是:

\begin{aligned} F = \frac{G m_{E} m_{o}}{(r_{E} + h)^{2}} \end{aligned}

Because

\begin{aligned} h \end{aligned}

is much smaller than

\begin{aligned} r_{E} \end{aligned}

near the surface of Earth, we approximate that:

\begin{aligned} r_{E} + h \approx r_{E} . \end{aligned}

We can rewrite the force of gravity equation as:

\begin{aligned} F = \frac{G m_{E}}{r_{E}^{2}} \times m_{o} = m_{o} \times g_{E} \end{aligned}

Here, we grouped all the constant values and called it

\begin{aligned} g_{E} \end{aligned}

, where:

\begin{aligned} g_{E} = \frac{G m_{E}}{r_{E}^{2}} \approx 9.81. \end{aligned}

This might look familiar! We call

\begin{aligned} m g_{E} \end{aligned}

an object’s . Unlike an object’s mass, its weight can change depending on the amount of gravitational force on it!
::F=GmEmo(rE+h)2 因为h比靠近地球表面的 rE要小得多, 我们估计: rE+hrE。我们可以重写重力方程式的力量 : F=GmErE2xmo=moxgE 此处, 我们将所有恒定值分组, 称它为 gE, 即: gE=GmErE29. 81。这看起来可能很熟悉。我们称 mgE 为对象的。与物体的质量不同, 它的重量可能随物体的重力大小而变化。

Calculating Your Attraction to Your Friend
::计算您对朋友的吸引力

Suppose you and your friend are 2 meters apart. If you have a mass of 60 kg and your friend has a mass of 70 kg, the gravitational force between you can be calculated as follows:
::假设你和你的朋友相距2米。如果质量为60公斤,而你的朋友质量为70公斤,那么你们之间的引力可以计算如下:

Write Newton's Equation:
::写入牛顿方程式 :

\begin{aligned} F = \frac{G m_{1} m_{2}}{r^{2}} \end{aligned}

::F=Gm1m2r2

Substitute the values:
::替代值:

\begin{aligned} F = \frac{(6.67 \times 10^{- 11} {Nm}^{2} {/kg}^{2}) \times (60 kg) \times (70 kg)}{(2 m)^{2}} \end{aligned}

::F=(6.67×10-11 Nm2/kg2)×(60公斤)×(70公斤)×(70公斤)(2米)2

Calculate the Answer:
::计算答案 :

\begin{aligned} F \approx 7 \times 10^{- 8} N \end{aligned}

Not enough to notice, but it’s there!
::不足以引起注意,

Newtons Apple Simulation
::牛顿苹果模拟

Use the Newton’s Apple simulation below to learn more about the Universal Law of Gravity and observe how this law unites the motion of objects on the Earth with the motion of all objects throughout our universe:
::用牛顿下面的苹果模拟来了解更多关于世界引力法则的知识, 并观察这部法律如何将地球上物体的运动与宇宙中所有物体的运动结合起来:

Summary
::摘要

Newton proposed the universal law of gravitational attraction as $\begin{aligned} F = G \frac{m_{1} m_{2}}{d^{2}} \end{aligned}$ .
::牛顿提出了引力吸引的普遍法则,作为F=Gm1m2d2。

Near Earth's surface, gravity creates a nearly constant acceleration, $\begin{aligned} g_{E} \approx 9.81 {m/s}^{2} . \end{aligned}$
::近地表面,重力产生接近恒定的加速度, gE9.81m/s2。

The universal gravitational constant, G, was determined by Cavendish to be 6.67 × 10 ^-11 N·m ² /kg ² .
::卡文迪什公司确定,全球引力常数G为6.67×10-11 N/m2/kg2。

::卡文迪什公司确定,全球引力常数G为6.67×10-11 N/m2/kg2。

Review
::回顾

The earth is attracted to the sun by the force of gravity. Why doesn’t the earth fall into the sun?
::地球被引向太阳的引力所吸引。为什么地球不掉入太阳呢?

If the mass of the earth remained the same but the radius of the earth shrank to one-half its present distance, what would happen to the force of gravity on an object that was resting on the surface of the earth?
::如果地球质量保持不变,但地球半径缩小到目前距离的一半,那么地球表面的物体的重力会怎样?

Lifting an object on the moon requires one-sixth the force that would be required to lift the same object on the earth because gravity on the moon is one-sixth that on earth. What about horizontal acceleration? If you threw a rock with enough force to accelerate it at 1.0 m/s ² horizontally on the moon, how would the required force compare to the force necessary to accelerate the rock in the same way on the earth?
::提升月球上的物体需要六分之一的力, 才能在地球上提升同样的物体, 因为月球的重力是地球的六分之一。水平加速如何? 如果您投掷一块具有足够强度的岩石, 在月球上水平在1.0 m/ s2 水平加速, 所需的力如何与以同样方式加速地球岩石所需的力相比?

The mass of the earth is 5.98 × 10 ²⁴ kg and the mass of the moon is 7.35 × 10 ²² kg. If the distance between the earth and the moon is 384,000 km, what is the gravitational force on the moon?
::地球质量是5.98×1024公斤,月亮质量是7.35×1022公斤。如果地球与月球之间的距离是384,000公里,那么月球的引力是什么?

Explore More
::探索更多

Use this resource to answer the questions that follow.
::使用此资源回答下面的问题。

What is gravity?
::什么是重力?

What caused the sun to form?
::是什么使太阳形成?

What is the relationship between the strength of a gravitational force and distance?
::引力强度和距离之间的关系是什么?

What is the relationship between the strength of a gravitational force and mass?
::引力的力量和质量之间的关系是什么?

Resources
::资源

Does gravity effect everything at the same rate? The experiment in this MIT video helps to answer that question.
::重力是否以同样的速率影响一切?这段麻省理工学院视频的实验有助于回答这个问题。

Review
::回顾

What does Newton's Universal Law of Gravity state about the force between two objects?
::牛顿的《世界重力法》对两个物体之间的力有何规定?

The moon is attracted to the Earth by the force of gravity. Why doesn’t the Moon fall to the surface of the Earth?
::月球被重力吸引到地球,为什么月球不掉到地球表面?

::月球被重力吸引到地球,为什么月球不掉到地球表面?

Use the formula $\begin{aligned} F = \frac{G m_{1} m_{2}}{r^{2}} \end{aligned}$ to calculate the gravitational force between two 10 kg masses that are 2 meters apart.
::使用公式F=Gm1m2r2来计算两个10千克质量之间2米的引力。

::使用公式F=Gm1m2r2来计算两个10千克质量之间2米的引力。

Mars' gravitational force on a 1 kg object is 3.71 N. Use this information to estimate Mars' mass, given that its radius is $\begin{aligned} 3.39 \times 10^{6} m \end{aligned}$ .
::1公斤物体上的火星引力为3.71 N. 使用这一信息估计火星的质量,因为其半径为3.39×106m。

::1公斤物体上的火星引力为3.71 N. 使用这一信息估计火星的质量,因为其半径为3.39×106m。

Why does r in the gravitational equation approximate Earth’s radius when calculating gravity near the surface?
::为什么在重力方程式中,当计算接近表面的重力时, 地球的半径接近地球的半径?

::为什么在重力方程式中,当计算接近表面的重力时, 地球的半径接近地球的半径?

Imagine you are on the Moon. How would the gravitational force on you compare to when you are on Earth, and what is the reason?
::想象一下你是在月球上。你身上的引力如何与你在地球上时相比? 原因何在?

::想象一下你是在月球上。你身上的引力如何与你在地球上时相比? 原因何在?

章节大纲

常规

牛顿的万国引力法

Force of Gravity ::重力力

Discovering the gravitational constant ::发现引力常数

Calculating Earth's Mass ::计算地球质量

First, convert the radius into meters: ::首先,将半径转换成米:

Gravity Near the Earth's Surface ::近地球表面的重力

Calculating Your Attraction to Your Friend ::计算您对朋友的吸引力

Newtons Apple Simulation ::牛顿苹果模拟

Summary ::摘要

Review ::回顾

Explore More ::探索更多

Resources ::资源

Review ::回顾

Force of Gravity
::重力力

Discovering the gravitational constant
::发现引力常数

Calculating Earth's Mass
::计算地球质量

First, convert the radius into meters:
::首先,将半径转换成米:

Gravity Near the Earth's Surface
::近地球表面的重力

Calculating Your Attraction to Your Friend
::计算您对朋友的吸引力

Newtons Apple Simulation
::牛顿苹果模拟

Summary
::摘要

Review
::回顾

Explore More
::探索更多

Resources
::资源

Review
::回顾