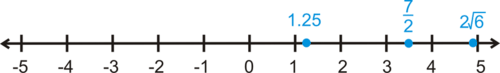Course: 1.3 真实数字子集

Section outline

Select section General

Collapse Expand
General

Collapse all Expand all
- Select activity 新闻通告
  
  新闻通告 Forum

真实数字的子集

Computers process some types of numbers differently than others. If a decimal number continues forever without stopping and without a pattern , then it is can be classified as an irrational number. However, a computer has to limit the number of digits it can process, so that it can interpret the number. A type of decimal number that terminates is an example of a rational number . These two types of decimal numbers are elements of subsets of what is called the set of real numbers. We explore the real numbers in this section.
::计算机处理某些类型的数字。如果一个小数数在不停止和没有模式的情况下永久持续下去, 那么它可以被归类为非理性数字。但是, 计算机必须限制它可以处理的数字数, 以便解释数字。一个终止的小数数是合理数字的一个例子。这两类小数数是被称为真实数字组子集的元素。我们在本节中探索真实数字。

lesson content

Real Numbers and Important Subsets
::真实数字和重要子集

There are several types of subsets of real numbers —numbers that can be expressed as a decimal. You are probably familiar with fractions, decimals, and counting numbers from your daily life. (The counting numbers are 1,2,3,....) All of these types of numbers are real numbers.
::真实数字子集有几种类型——数字可以以小数表示。您可能熟悉日常生活中的分数、小数和计数。 (计数数为 1,2,3,...)所有这些类型数字都是真实数字。

The table below describes important subsets of the real numbers.

::下表说明了实际数字的重要子集。

Real Numbers	Any number that can be expressed as a decimal. Symbol: $\begin{align}\mathbb{R}\end{align}$ ¹	Examples: $\begin{align}8, 4.67, - \frac{1}{3}, \pi\end{align}$
Rational Numbers	Any number that can be written as a fraction , $\begin{align}\frac{p}{q}\end{align}$ , where p and q are integers . In decimal form, these are terminating decimals, and non-terminating, repeating decimals. Symbol: $\begin{align}\mathbb{Q}\end{align}$	Examples: $\begin{align}-\frac{5}{9},\frac{1}{8},1.\overline{3},\frac{16}{4}, 0.124\end{align}$
Irrational Numbers	When written as a decimal, these numbers do not terminate or repeat. Symbol: $\begin{align}\mathbb{I}\end{align}$ (although this is not universally used to represent the irrational numbers)	Examples: $\begin{align}e, \pi, -\sqrt{2},\sqrt[3]{5}\end{align}$
Integers	All counting numbers, their negatives, and zero. The set {...,-3,-2,-1,0,1,2,3,...}. Symbol: $\begin{align}\mathbb{Z}\end{align}$	Examples: -65,0,192 ::例如:-65,0,192
Whole Numbers	All positive counting numbers and zero. The set {0,1,2,3,...}.	Examples: 0,5,12,78
Natural Numbers	All positive counting numbers. The set {1,2,3,...}. Symbol: $\begin{align}\mathbb{N}\end{align}$	Examples: 11,59

¹ The symbols for the subsets are usually handwritten as a capital letter with a line through it since we cannot handwrite in bold.
::1 子集的符号通常用手写成大写字母,有一条横线,因为我们无法用黑体手写。

The subsets of the real numbers can be represented in a Venn diagram as follows:
::真实数字的子集可以在Venn图中显示如下:

lesson content

Note: Real numbers are a subset themselves of the complex numbers. We will addres s complex (or imaginary) numbers in the Quadratic Functions chapter.
::注:实际数字是复杂数字的一个子集。我们将在“二次函数”章节中处理复杂(或想象中)数字。

Example 1
::例1

To which subsets of the real numbers does -7 belong?
::真实数字 -7属于哪个子集?

Solution: -7 is a rational number and an integer.
::解答: - 7是一个合理的数字和一个整数。

Example 2
::例2

List all the subsets that 1.3 lies in.
::列出1.3中的所有子集。

Solution: 1.3 is a terminating decimal. Therefore , it is a rational number. As a fraction, we would write $\begin{align*}\frac{13}{10}\end{align*}$ because the 3 is in the tenths position after the decimal. It is also a real number . This counts as one of the subsets since the set of real numbers is a subset of itself as all sets are.
::解答 : 1. 3 是终止的小数小数。因此, 它是一个合理的数字。作为分数, 我们会写入 1310, 因为小数小数后三位居十分位。它也是一个真实的数字。这算作子数之一, 因为真实数字组和所有组数一样是子数本身的子数。

Example 3
::例3

True or False: $\begin{align*} \frac{8}{3}\end{align*}$ is an irrational number.
::真理或假:83是一个非理性的数字。

Solution: False. Even though, i t can be expressed as a non-terminating decimal, 2.66666666... or $\begin{align*}2.\overline{6}\end{align*}$ , the decimal part repeats. It can also be written as a fraction with an integer in the numerator and the denominator. It is a rational number.
::解答: 假的。即使它可以表示为非终止的小数小数, 2. 6666666666... 或 2. 6, 小数部分重复。也可以以数字和分母中一个整数的分数写成。它是一个合理的数字。

Example 4
::例4

S ay a computer outputs $\begin{align*}\sqrt{5}\end{align*}$ as an answer. To process it, the computer limits the number of digits after the decimal point to 8, so we get 2.2360679775. What subsets of the real numbers can we use to categorize $\begin{align*}\sqrt{5}\end{align*}$ and 2.2360679775.
::以计算机输出5 作为答案。要处理它, 计算机将小数点后的数字限制在小数点后为 8 。因此我们得到 22360679775。真实数字中的哪些子集可以用来分类 5 和 22360679775 。

Solution: $\begin{align*}\sqrt{5}\end{align*}$ is an irrational number because when it is converted to a decimal it does not end or repeat. 2.2360679775 is a rational number because it is a terminating decimal.
::解决方案:5是一个不合理的数字,因为当转换成小数点时,它不会结束或重复。 2.2360679775是一个合理的数字,因为它是一个终止的小数点。

by Mathispower4u provides several examples of classifying numbers by which subsets of the real numbers they belong to.
::由 Mathispower4u 提供数字分类的几个例子,通过这些数字的实际子集来分类。

Example 5
::例5

Let $\begin{align*}A = \{-2, 34 , \sqrt{2} , \sqrt{9} , \pi \}\end{align*}$ . L ist all of the elements of A that are rational numbers.
::A2,34,2,9,9。列出A中所有合理数字的元素。

Solution: Rational numbers can be written as fractions where the numerator and the denominator are integers. This is true for $\begin{align*}-2,34, \sqrt{9}\end{align*}$ . As fractions, we have
::解析度: 当分子和分母为整数时, 理性数字可以写成分数。这在 - 2, 34,9. 分数中是这样。作为分数, 我们可以看到。

\begin{aligned} - 2 = \frac{- 2}{1} & 34 = \frac{34}{1} & \sqrt{9} = 3 = \frac{3}{1} \end{aligned}

$\begin{align*}-2=\frac{-2}{1} && 34=\frac{34}{1} && \sqrt{9}=3=\frac{3}{1}\end{align*}$

Example 6
::例6

True or False: $\begin{align*}-\sqrt{9}\end{align*}$ is an irrational number.
::真理或假:-9是一个非理性的数字。

Solution: $\begin{align*}-\sqrt{9}=-3\end{align*}$ , which is an integer. The statement is false.
::解析度 : - 93, 是一个整数。语句是虚假的。

Real Number Line
::实数行

We can represent the real numbers graphically on the real number line . The real number line has an origin, the point 0 since 0 is neither positive or negative. The positive numbers are larger than 0 and are represented on the right side of the number line. The negative numbers are less than 0 and are represented on the left side of the number line. The numbers on the number line increase as you go from left to right.
::我们可以以图形形式在实际数字线上代表真实数字。实际数字线有一个来源, 点 0 而不是正数或负数。正数大于0, 并在数字线的右侧表示。负数小于0, 在数字线的左侧表示。数字线上的数字随着从左向右增加。

lesson content

To represent a number on the number line graphically, we plot a point or its coordinate where it is located on the number line. We cannot do this perfectly in all cases, so sometimes we approximate where the number is located.
::要用图形方式在数字线上表示数字, 我们绘制一个点或其坐标, 它位于数字线上。我们无法在所有情况中完全做到这一点, 因此有时我们大致估计数字的位置。

Example 7
::例7

Plot $\begin{align*}1.25, \frac{7}{2}\end{align*}$ , and $\begin{align*}2\sqrt{6}\end{align*}$ on a number line.
::计 1.2572 和26 在数字线上。

Solution: To plot these numbers, it is helpful to convert them all to decimals. $\begin{align*}1.25, \frac{7}{2}=3.5\end{align*}$ , and $\begin{align*}2\sqrt{6}\approx 4.899\end{align*}$ (The symbol $\begin{align*}\approx\end{align*}$ means approximately .) Draw your number line and plot the points. You can choose to draw hash marks at half-values or only even values or any other regular interval.
::解析 : 要绘制这些数字, 将其转换为小数将很有帮助。 1. 25, 72=3.5 和 264. 899 (符号意指约。) 绘制您的数字线并绘制点。您可以选择以半值或仅以数值或其它常规间隔来绘制散列标记。

lesson content

1.25 = 1 $\begin{align*}\frac{1}{4}\end{align*}$ . Therefore, we need to place a point about 1/4 of the way past 1 or 1/4 of the distance between 1 and 2.
::1.25 = 114。因此,我们需要将距离1至2之间距离1或1/4的距离定在四分之一左右。

$\begin{align*}\frac{7}{2}\end{align*}$ = 3.5. Therefore, the number is halfway between 3 and 4, so we place a point halfway between 3 and 4.
::72 = 3.5。因此,这个数字在3到4之间的中间点,所以我们把3到4之间的中间点放在3到4之间的中间点。

$\begin{align*}2\sqrt{6}\end{align*}$ is a little less than 5, so we place a point a little to the left of 5 on the number line.
::26小于5 所以我们在数字线上向5的左侧放一点点

Summary
::摘要

The real numbers have the following important subsets: rational numbers, irrational numbers, integers, whole numbers, and natural numbers.
::真实数字有以下重要的子集:合理数字、非理性数字、整数、整数和自然数字。

To represent a number on the number line graphically, we plot a point or its coordinate where it is approximately located on the number line.

::要用图形方式在数字线上表示数字,我们绘制一个点或其坐标,将其大致放在数字线上。

Review
::回顾

What is the most precise (smallest) subset of real numbers that the following numbers belong in?
::以下数字属于哪些实际数字中最精确(最小)的子集?

1. 5.67

2. $\begin{align*}-\sqrt{6}\end{align*}$

3. $\begin{align*}\frac{9}{5}\end{align*}$

4. 0

5. -75

6. $\begin{align*}\sqrt{16}\end{align*}$

List all of the subsets of the real numbers to which the following numbers belong.
::列出下列数字所属的真实数字的所有子集。

7. 4

8. $\begin{align*}\frac{2}{3}\end{align*}$

9. $\begin{align*}\pi\end{align*}$

Determine if the following statements are true or false.
::确定以下声明是真实的还是虚假的。

10. Integers are rational numbers.
::10. 整数是合理数字。

11. Every whole number is a real number.
::11. 每个数字都是真实数字。

12. Integers are irrational numbers.
::12. 整数是非理性数字。

13. A natural number is a rational number.
::13. 自然数字是一个合理的数字。

14. An irrational number is a real number.
::14. 非理性数字是一个实际数字。

15. Zero is a natural number.
::15. 零是一个自然数字。

Explore More
::探索更多

1. How do we write 0.14141414.... as a fraction? Let's devise a step-by-step process.
::1. 我们如何将0.14141414作为分数写成0.14141414?让我们设计一个逐步的过程。

Step 1: Set your repeating decimal equal to x .

\begin{aligned} x = 0.14141414 \end{aligned}

$\begin{align*}x = 0.14141414\end{align*}$
::第1步:将重复的小数小数数设为 x. x=0. 14.141414

Step 2: Find the repeating digit(s). In this case, 14 is repeating.
::第2步:查找重复的数字。在此情况下,14个数字正在重复。

Step 3: Move the repeating digits to the left of the decimal point and leave the remaining digits to the right.
::第3步:将重复的数字移到小数点左边,将其余的数字移到右边。

\begin{aligned} 14.14141414 \end{aligned}

$\begin{align*}14.14141414\end{align*}$

Step 4: Multiply x by the same factor you multiplied your original repeating decimal to get your new repeating decimal.
::第4步:乘以X乘以与乘以原来的重复小数位数相同的因数,以获得新的重复小数位数。

\begin{aligned} 14.14141414 = 100 (0.14141414) \end{aligned}

$\begin{align*}14.14141414 = 100(0.14141414)\end{align*}$

So,

\begin{aligned} 100 x = 14.14141414 \end{aligned}

$\begin{align*}100x = 14.14141414\end{align*}$
::所以,100x=14.14141414

Step 5: Solve your system of linear equations for x .
::步骤5:解决 x 的线性方程式系统。

\begin{aligned} 100 x = 14.14141414 \\ - \underline{x = 0.14141414} \\ 99 x = 14 \\ x = \frac{14}{99} \end{aligned}

$\begin{align*}100x = 14.14141414 \\ -\underline{\ \ \ \ x = \ \ 0.14141414} \\ 99x = 14\\ \\ x = \frac{14}{99}\end{align*}$
::100x=14.14141414- x=0.14141414_99x=14X=1499

What about 0.327272727... ? The 0.3 does not repeat. So, rewrite this as $\begin{align*}0.727272727...-0.4\end{align*}$ Therefore, the fraction will be:
::0.3272722727... 0. 3不重复。所以, 重写为 0. 727272727272727... - 0. 4。因此, 分数将是 :

\begin{aligned} \frac{72}{99} - \frac{4}{10} \\ \frac{8}{11} - \frac{2}{5} \\ \frac{40}{55} - \frac{22}{55} \\ \frac{18}{55} \end{aligned}

$\begin{align*}\frac{72}{99}-\frac{4}{10}\\ \frac{8}{11}-\frac{2}{5}\\ \frac{40}{55}-\frac{22}{55}\\ \frac{18}{55}\end{align*}$

Rewrite the following repeating decimals as fractions.
::将以下重复的十进制数重写为分数。

a. 0.4646464646...
::a. 0.4646464646...

b. 0.81212121212...
::b. 0.812121212121212...

2. Irrational numbers can be approximated by a sequence of rational numbers. For example, $\begin{align*}\sqrt{2}\end{align*}$ = 1.4, 1.41, 1.414, 1.4142, 1.41421, ... . Find the first five rational numbers in the sequence for $\begin{align*}\sqrt{3}\end{align*}$ .
::2. 不合理数字可以用一个合理数字序列来近似。例如,2 = 1.4, 1.41, 1.414, 1.4142, 1.4421, ...。在顺序中查找3 的前五个合理数字。

3. Judy answered the following scores on her math quizzes this semester. Convert her scores to percentages, rounding to the nearest whole number and order her quiz scores from least to greatest.
::3. 朱迪在本学期的数学测验中回答以下分数:将分数转换成百分数,四舍五入到最近的整数,并命令她的测验分数从最少到最多。

Quiz 1: $\begin{align*}\frac{19}{22}\end{align*}$
::问题1:1922年

Quiz 2: $\begin{align*}\frac{29}{33}\end{align*}$
::问题2:2933

Quiz 3: $\begin{align*}\frac{16}{19}\end{align*}$
::问题3:1619

4. John’s score report from a standardized test indicates that he answered 57.1428571428… % of the questions correctly. There were seven short answer questions on the test. How many did John answer correctly?
::4. 约翰的标准化测试成绩报告表明,他正确回答了57.1428571428.%的问题,测试有七个简短的回答问题,约翰回答正确了吗?

5. A farmer has a field with an area measuring 600.72 square meters. Yesterday, he sprayed two-thirds of the field with insecticide.
::5. 农民有一个面积600.72平方米的田地,昨天他喷洒了三分之二的田地杀虫剂。

a . Which of the following set of numbers does the area of the field fall into?
::a. 实地地区属于下列哪一组数字?

b. Which of the following set of numbers does the fraction of the field that was sprayed fall into?
::b. 喷洒的田地部分属于下列哪一组数字?

Integers, Rational numbers, Irrational numbers, Natural numbers, Whole numbers
::整数、合理数字、不合理数字、自然数字、整数

6. Which subset of real numbers would you use in the scenarios below?

::6. 在下文的假设情景中,你将使用哪个子集的实际数字?

a. money in your bank account

::a. 银行帐户中的款项

b. population of your town

::b. 城镇人口

c. elevation compared to sea level

::c. 与海平面相比的海平面升高

Answers for Review and Explore More Problems
::回顾和探讨更多问题的答复

Please see the Appendix.
::请参看附录。

PLIX
::PLIX

Try this interactive that reinforces the concepts explored in this section:
::尝试这一互动,强化本节所探讨的概念:

Section outline

General

真实数字的子集

Real Numbers and Important Subsets ::真实数字和重要子集

Example 1 ::例1

Example 2 ::例2

Example 3 ::例3

Example 4 ::例4

Example 5 ::例5

Example 6 ::例6

Real Number Line ::实数行

Example 7 ::例7

Summary ::摘要

Review ::回顾

Explore More ::探索更多

Answers for Review and Explore More Problems ::回顾和探讨更多问题的答复

PLIX ::PLIX

Real Numbers and Important Subsets
::真实数字和重要子集

Example 1
::例1

Example 2
::例2

Example 3
::例3

Example 4
::例4

Example 5
::例5

Example 6
::例6

Real Number Line
::实数行

Example 7
::例7

Summary
::摘要

Review
::回顾

Explore More
::探索更多

Answers for Review and Explore More Problems
::回顾和探讨更多问题的答复

PLIX
::PLIX