1.16 几何公式
章节大纲
-
The front of the house below is shaped like a pentagon. We want to find how much paint we need to paint the front of the house. To determine this, we need to find the number of square feet or the area of the pentagon. W e discuss how to find quantities like the area with geometric formulas in this section .
::下面的房屋前部形状像五角形。 我们想要找到需要多少油漆来油漆房屋前部。 要确定这一点, 我们需要找到平方英尺或五角形面积。 我们讨论如何找到像此区域一样的数量, 并在此部分使用几何公式 。
Two-Dimensional Shapes
::两种不同型形状In this section, we will discuss two-dimensional shapes , shapes that have length and width, and three-dimensional shapes , shapes that have length, width, and height.
::在本节中,我们将讨论二维形状、长宽的形状和三维形状、长、宽和高度的形状。Polygons and circles are the two-dimensional shapes that we will focus on in this section. Polygons are shapes with sides that are line segments and those line segments meet at their endpoints. Circles are shapes where all of the points are the same distance from a given point, the center.
::多边形和圆圈是我们在本节中要关注的二维形状。多边形是两边的形状,两边是线条段,这些线条部分在终点相交。圆圈是形状,所有点与一个指定点,即中点的距离相同。The box below shows some common polygons and a circle.
::以下框显示一些共同多边形和圆。Polygons and Circles
::多边形和圆形-
Triangle, 3 sides
::三角三角, 3 边 -
Quadrilateral, 4 sides
::四方,四面四面四面四面四面四面四面四方 -
Pentagon, 5 sides
::五角五角,五面 -
Hexagon, 6 sides
::六边六边六边六角 -
Octagon, 8 sides
::八面八面八角 -
Circles

::圆环
Perimeter and Circumference
::周边和环极Perimeter and circumference both measure the distance around a shape. For polygons, we call that distance the perimeter. For circles, we call that distance the circumference.
::周围和环绕都测量形状周围的距离。对于多边形,我们称之为周界。对于圆圈,我们称之为环形的距离。Perimeter
::周边To find the perimeter of a polygon, we add up the lengths of the sides. We can express some of these as formulas for special shapes.
::为了找到多边形的周界,我们把两边的长度加起来。我们可以用特殊形状的公式来表示其中的一部分。Perimeter Formulas
::周边公式-
Equilateral triangle (a triangle where all the sides are equal):
::等边三角形( 所有边相等的三角形): P=3 -
Parallelogram (a quadrilateral where two sets of opposite sides are parallel), a rectangle is an example:
::平行形(两组对面平行的四边形),矩形就是一个例子:P=2l+2w -
Square:
::方块:P=4
Example 1
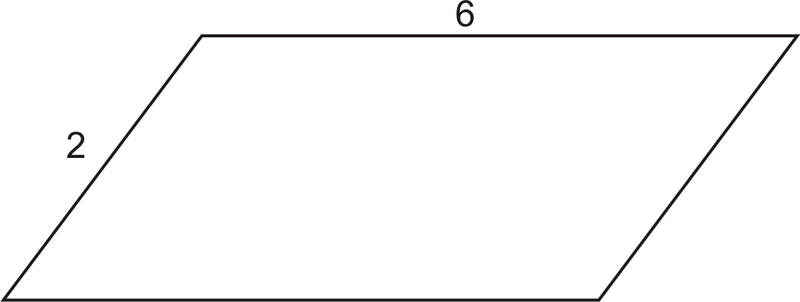
::例1Find the perimeter of the parallelogram below.
::在下面找到平行图的周界Solution: The length is 6 units and the width is 2 units. Substituting these values into the formula gives us
::解答: 长度为 6 个单位, 宽度为 2 个单位。 将这些值替换为公式 。
::P=2l+2w=26+22=12+4=16The perimeter of this parallelogram is 16 units.
::这一平行图的周界是16个单位。Example 2
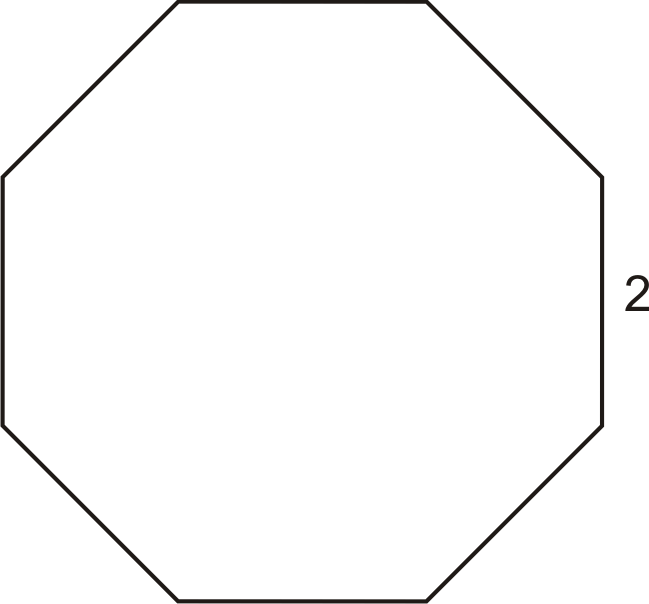
::例2Find the perimeter of the shape below. Assume all of the sides are the same length.
::找到下面形状的周界。 假设所有侧面的长度相同 。Solution: This is an octagon. To find the perimeter, we need to add up all of the sides. Since there are eight sides and they are all of length 2, we can compute
::解决方案: 这是八角形。 要找到周界, 我们需要将方形加起来。 因为有八面, 它们都是长度 2, 我们可以计算
::P=2+2+2+2+2+2+2+2+2+2=8=8=2=16The perimeter of this octagon is also 16 units.
::该八边形的周边还有16个单元。by Mathispower4u demonstrates how to find the perimeter of polygons.
::Mathispower4u 演示如何找到多边形的周界。Circumference
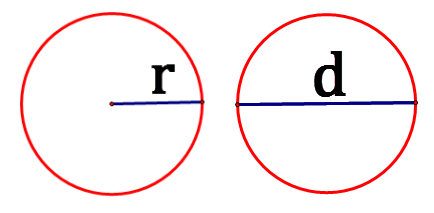
::环环境To find the circumference of a circle, we need to know the length of the radius or the diameter. The radius is the distance between the center and any of the points on the circle. The diameter is the length of the line segment from one end of the circle to the other end through the center. It is the sum of two radii.
::要找到圆的环绕度, 我们需要知道圆的半径或直径的长度。 半径是中间和圆上任何一点之间的距离。 直径是圆一端到中间另一端的线段长度。 这是两个弧度的总和 。The circumference formula also includes the number (pi). We use the Greek letter to represent the number 3.14159265358979323846…, an irrational number that we get by dividing the circumference of a circle by its diameter . Since is an irrational number, the digits in the decimal of go on and on forever with no pattern . Mathematicians using computer programs have calculated to over two quadrillion decimal places, yet no pattern in the digits has been identified. A quick approximation of is . However, this is not exactly right. A better approximation (but still not exact) is . We often approximate with a decimal as 3.14. 1
::环形公式中还包括 {( pi) 。 我们使用希腊字母 _ 来表示数字 3.1415926535898979323846..., 这个不合理的数字是用圆的直径来将圆的环形除以其直径而得到的。 由于 __ 是一个不合理的数字, 小数中的数字是 __ 继续, 并且永远没有模式。 使用计算机程序的数学家计算出 __ 至 小数小数点中的两个位数, 但数字中还没有确定任何模式 。 } 快速近似 __ 是 227 。 但是, 这不完全正确 。 更好的近似( 但仍不准确) 是 355113 。 我们常常以小数点为 3. 1.41 的近似 。With , we can find the distance around a circle using the formulas in the box below.
::使用下方框中的公式,我们可以找到圆圆周围的距离。Circumference Formulas
::环环境公式-
When you know the radius,
.
::当你知道半径,C=2r。 -
When you know the diameter,
.
::当你知道直径时,CD。
Example 3
::例3The tires on a compact car are 18 inches in diameter. How far does the car travel after the tires turn once?
::一辆紧凑车的轮胎直径18英寸,轮胎转过一次后车程有多远?Solution: The distance the car travels after one rotation of the tires is the circumference. Since we know the diameter of the tires, we can use the formula, , to find the distance covered over one rotation.
::解答: 汽车在轮胎一次旋转后行驶的距离是环形。 由于我们知道轮胎的直径, 我们可以使用配方CD, 来找到一个旋转时行驶的距离 。
The car travels 56.55 inches.
::Cd18=56. 54866776... 56.55 汽车行驶56.55英寸。This video by CK-12 demonstrates how to calculate the circumference of a circle.
::CK-12的这段视频展示了如何计算圆环。Area
::地区面积The area of a shape is a measurement of the amount of space inside of the shape. For example, if you were tiling a floor, the area would be the number of square feet that you tile. Area is measured in square units, because area has two dimensions . Some formulas for common shapes are below.
::形状区域是测量形状内面积的尺度。例如,如果您在地板上铺平一个平方英尺的平方英尺,那么这个区域就是您平方英尺的平方英尺。区域用平方平方平方平方英尺测量,因为区域有两个维度。一些通用形状的公式在下面。Area Formulas
::区域公式-
Triangle:
, where
b
= base,
h
= height
::三角形:A=12bh,b=基数,h=高度 -
Parallelogram:
::平行图: A=bh -
Rectangle:
, where
l
= length,
w
= width
::矩形: A=lw, 其中l=长度, w=宽度 -
Square:
, where
s
= length of one of the sides
::方块:A=s2,其中s=一面的长度 -
Trapezoid:
, where
b
1
and
b
2
= base 1 and base 2, respectively
::A=12(b1+b2)h,其中b1和b2分别=基数1和基数2 -
Circle:
, where
r
= radius
::圆 : Ar2, 其中 r = 半径
Example 4
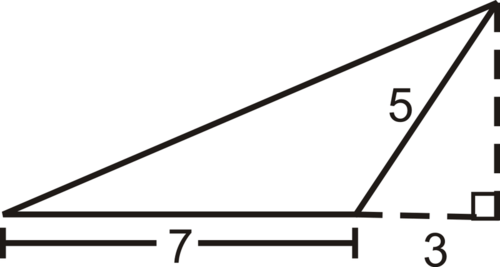
::例4Find the area of the triangle below.
::查找下方三角形的区域 。Solution: To find the area of this triangle we need to know the measure of the base and the measure of the height. The base or bottom of this triangle is 7 units. The vertical height of this shape is unknown. It is not 5 because that side is not vertical. We can find the height using the information in the dashed section. The triangle formed from the dashed section is a right triangle, so we can use the Pythagorean Theorem to find the length of the missing side.
::解决方案 : 要找到此三角形的区域, 我们需要知道基数的大小和高度的大小。 此三角形的底部或底部是 7 个单位。 此形状的垂直高度未知。 不是 5 个 , 因为侧面不是 垂直 。 我们可以使用破折线区域的信息找到高度 。 从破折线区域形成的三角形是一个右三角形, 这样我们就可以使用 Pythagorian Theorem 来找到缺失侧的长度 。The Pythagorean Theorem states that in a right triangle the square of the length of the hypotenuse (longest side, located across from the right angle) is equal to the sum of the squares of the other two sides, called legs. In the Pythagorean Theorem, = the length of one of the legs, b = the length of the other leg, c = the length of the hypotenuse.
::Pythagoren Theorem指出,在右三角形中,下层长度的正方形(最长方,位于右角对面)等于其他两侧的正方形之和,称为腿。在Pytagoren Theorem, a = 腿的长度,b = 另一腿的长度,c = 下层长度。
::a2+b2=c232+b2=529+b2=25b2=16b2=16b=4The height of the triangle is 4 units. Now, we can find the area of the triangle.
::三角形的高度是4个单位。现在,我们可以找到三角形的区域。The area is 14 square units.
::A=12bh=1274=14 面积为14平方单位。WARNING
::警告The height of the shape is not always the same as the length of one of the sides. The height is the vertical height. For example, when you go to the doctor, they do not measure your height by asking you to lean to the side.Example 5
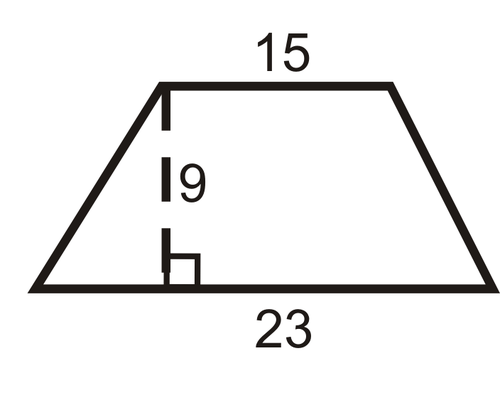
::例5Find the area of the trapezoid below.
::找到下面的捕捉细胞的区域Solution: To find the area of a trapezoid, we need to identify the two bases and determine the height. The height is given and is 9 units. The two bases are 15 units and 23 units. Using the formula for the area, we have
::解决方案: 要找到一个陷阱类的面积, 我们需要确定两个基点并确定高度。 给定高度为 9 个单位。 两个基点为 15 个单位和 23 个单位。 使用此区域的公式, 我们发现
::A=12(b1+b2)h=12(15+239)9=12-38-9=171The area is 171 square units.
::面积为171平方单位。by CK-12 demonstrates how to find the area and perimeter of a trapezoid.
::由CK-12演示如何找到一个的面积和周界。Example 6
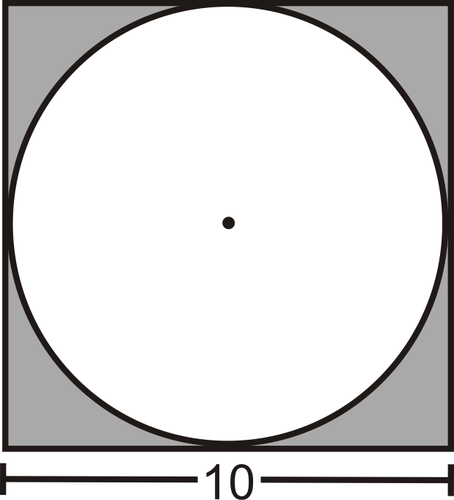
::例6A circle is inscribed in a square. Each side of the square is 10 cm long. What is the area of the circle?
::以正方形标出一个圆形。正方形的每侧长10厘米。圆的面积是多少?Solution: To find the area of a circle, we need to know the radius. A radius is not drawn here, but we can determine the diameter. The length of one side of the square is also the length from one side of the circle to the other through the center, so the diameter is 10 units. The radius of the circle is half the length of the diameter or 5 units. Using the formula for the area of a circle, we have:
::解析 : 要找到圆的面积, 我们需要知道圆的半径 。 半径不在这里绘制, 但我们可以确定直径 。 方形的一边长度也是圆的一边到中间的另一边的长度, 因此直径是 10 个单位 。 圆的半径是直径的半径的一半 或 5 个单位 。 使用圆的公式, 我们拥有 :
The area is approximately 78.54 square units.
::Ar252=2578.539816... 78.54 面积约为78.54平方单位。Three-Dimensional Shapes
::三种不同类型形状Three-dimensional shapes or solids , are shapes that have a length, a width, and a height. One class of solids is prisms . Prisms have two parallel bases that are the same. Some examples of prisms are below.
::三维形状或固态,是长、宽和高的形状。一类固体是棱晶。棱晶有两个相同的平行基。棱晶的一些例子在下面。Cylinders are similar to prisms in that the two parallel bases are circles.
::气瓶与棱晶相似,因为两个平行基地是圆形的。Other common solids include cones, pyramids , and spheres .
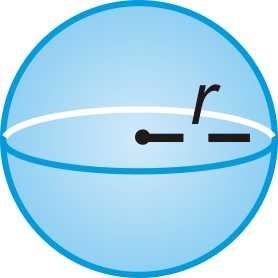
::其他共同固体包括锥体、金字塔和球体。Surface Area and Volume
::地表面积和面积For solids there are analogous ideas to perimeter and area. The area of the outside of the shape is called the surface area and the space inside the shape is called the volume .
::对于固态而言,其周围和面积有相似的概念。形状外的面积称为表面面积,形状内的空间称为体积。Surface Area
::地表地区The surface area of a shape is the area of the outside of the shape. For example, if you were wrapping a present in a rectangular (prism) box, the square inches of gift wrap used would be the surface area. Surface area is measured in square units, because it has two dimensions. Some formulas for common solids are below.
::形状的表面积是形状外的面积。例如,如果您在矩形(棱柱)框中包住一个显示,那么使用的礼品包的平方英寸将是表面面积。表面面积用平方单位测量,因为它有两个维度。一些普通固体的公式在下面。Surface Area Formulas
::表面面积公式-
Prism:
::棱晶:每个面孔的面积总和 -
Cylinder:
::气瓶: 基数+2的S=2区域 -
Cube:
::立方:S=6 -
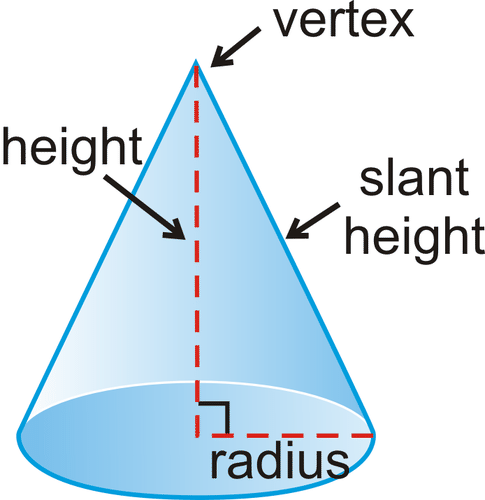
Cone:
,
l
is the length of the slant height
::Cone: Sr2rl,l 是倾斜高度的长度 -
Pyramid:
,
n
is the number of triangular faces,
b
is the length of the base, and
l
is the slant height
::金字塔: 基数+12nbl 的S=区域, n 是三角形面数, b 是基数长度, I 是倾斜高度 -
Sphere:
::球体: S=4°r2
Example 7
::例7How much gift wrap do you need to wrap a rectangular box that is 12 inches by 8 inches by 4 inches?
::要包装一个12英寸乘8英寸乘4英寸的矩形盒子 需要多少礼物包?Solution: A rectangular box is a rectangular prism. To find the surface area, we find the area of the base, . We then multiply that by the height of the box, 4 inches. . 384 square inches are required to wrap the present.
::解析度: 矩形框是一个矩形棱柱。 要找到表面区域, 我们找到基点的区域, A=lw= 128=96。 然后我们乘以框的高度, 4英寸。 S=基点的面积=964=384. 需要384 平方英寸才能包住当前。Example 8
::例8How much rubber is necessary to cover an NBA basketball?
::覆盖NBA篮球需要多少橡胶?Solution: The radius of a regulation NBA basketball is approximately 4.75 inches. 2 Using the formula for surface area, we have . About 284 square inches of rubber is necessary to cover a basketball.
::溶液:NBA篮球条例的半径约为4.75英寸。 2 使用表面积公式,我们有S=44.752283.53。 大约284平方英寸的橡胶是覆盖篮球所必需的。by Maria Anderson demonstrates how to find the surface area of a cylindrical solid.
::Maria Anderson展示了如何找到圆柱体固体的表面积。Volume
::量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量Volume is the amount of space inside of a three-dimensional shape. Volume is measured in cubic units because it has three dimensions. Some common volume formulas are below.
::音量是三维形状内的空格量。音量用立方体单位测量,因为它有三个维度。下面是一些共同的音量公式。Volume Formulas
::音量公式-
Prism:
::棱晶: V=基数的面积h -
Cylinder:
::气瓶:V=基数的面积 -
Cube:
::立方: V=s3 -
Cone:
::Cone: V=13°r2h -
Pyramid:
::金字塔: 基底的V=13 ' 地区 -
Sphere:
::球体: V=43°r3
Example 9
::例9How much ice cream can be put into an ice cream cone that has a diameter of 4 centimeters at the base and whose height is 10 centimeters?
::有多少冰淇淋能放进一个 直径为4厘米的冰淇淋锥里 其身高为10厘米的冰淇淋锥里?Solution: To find the volume of the cone, we need the radius and the height. The radius is one-half of the diameter or 2 centimeters. Using the formula, we have . You can put approximately 42 cubic centimeters of ice cream in the cone.
::溶液: 要找到锥体的体积, 我们需要方圆和高度。 半径为直径的半径或2厘米。 使用公式, 我们有 V= 13 22 10 42。 您可以在锥体中放置大约 42 立方厘米的冰淇淋 。Example 10
::例10A cylindrical grain silo has a diameter of about 10 feet and is 29.5 feet high. 3 Approximately, how much grain can the silo hold? Round your answer to the nearest cubic foot.
::圆柱形谷物筒仓直径约10英尺,高度29.5英尺。 3 大约该筒仓能维持多少谷物? 您的回答是最近的立方英尺。Solution: For the cylinder, we need to find the area of the circular base using the formula . The radius is one-half of the diameter or 5 feet. The area of the base is . The area of the base is approximately equal to 78.5 square feet.
::溶液:对于圆柱体,我们需要使用Ar2公式找到圆形基座的区域。半径为直径的一半或5英尺。基座的区域是A5278.5。基座的区域大约等于78.5平方英尺。To find the volume, we multiply the area of the base times the height. . The silo will hold about 2,316 cubic feet of grain.
::要找到体积, 我们将基数乘以高度。 V=基数的面积=78.529.5=2315.75。 筒仓将持有大约2 316立方英尺的谷物。by Lamee Storage demonstrates how to determine the volume formula for a pyramid by using the volume of a cube.
::Lamee Streating 演示如何使用立方体的体积来确定金字塔的体积公式。Summary
::摘要-
Perimeter and circumference measure the distance around the outside of a two-dimensional shape.
::周边和环绕测量了二维形状的外部距离。 -
Area measures the
surface of a
two-dimensional shape.
::区域测量二维形状的表面。 -
Surface area measures the area of the surface of a three-dimensional shape.
::表面面积测量三维形状表面面积。 -
Volume measures the space inside a three-dimensional shape.
::量度三维形状内的空间。
Review
::回顾Find the perimeter or circumference and the area of the shapes below .
::找出周围或环形 以及下面形状的区域-

-
To calculate the area,
use a height of 8.66 if you select 6 as your base.

::要计算区域,如果选择 6 作为基准,则使用8.66的高度。 -

-
To calculate area, use a height of 5 when the base is 12.

::要计算区域,当基数为12时,使用高度为5。 -

Find the surface area and the volume of the solids below.
::查找表面积和以下固体的体积。 -
To find the area of the triangle, use a height of 5.52 with 13 as the base.

::要找到三角形的区域,请使用5.52的高度,以13为基数。 -

-

-

-
Pyramid with square base and height of 17.

::金字塔,方形和高度为17度。 -
Sphere with radius of 12.
::球体半径为12。
Explore More
::探索更多1. The Great Pyramid of Giza was originally built around 2580-2560 BC and stood at a height of 481 feet. Over the years, the pyramid has shrunk due to exposure and age to a height of 455 feet. If the square base has a side length of 756 feet, what is the difference in the volume of the original pyramid and the current pyramid? 4
::1. 吉萨大金字塔最初建于公元前2580至2560年左右,高度481英尺,多年来,金字塔因暴露而缩小,年长455英尺,方形长756英尺,原始金字塔和当前金字塔的体积有何不同?
2. Mars is the second smallest planet in the Solar System. If Mars has a radius of 2,106 miles and Earth has a radius of 3,959 miles, what is the approximate difference in surface area between the two planets? 5 If Mars was habitable at the same rate as Earth, 35 people per square mile, how many people could live on Mars?
::2. 火星是太阳系中第二个最小的行星,如果火星的半径为2,106英里,地球的半径为3,959英里,那么这两个行星之间地表面积的大致差别是多少?5 如果火星与地球一样可以居住,每平方英里35人,有多少人可以生活在火星上?3. A net is a two-dimensional shape that can be folded into a three-dimensional shape. The image below is the net of a cube. The dashed lines are edges that need to be folded to create the cube.
::3. 网是一个二维形状,可以折叠成三维形状,下面的图像是立方体的网。破折线是创建立方体需要折叠的边缘。
Find the area of this shape if the sides of each square are 10 units. What is the surface area of the cube created from this net?
::如果每个方形的两边是 10 个单位, 则查找此形状的区域。 从此网中创建的立方体的表面积是多少 ?Answers to Review and Explore More Problems
::对审查和探讨更多问题的答复Please see the Appendix.
::请参看附录。PLIX
::PLIXTry this interactive that reinforces the concepts explored in this section:
::尝试这一互动,强化本节所探讨的概念:References
::参考参考资料-
“Pi,” last edited June 19, 2017,
.
::2017年6月19日编辑, -
“Basketball (ball),” last edited June 5, 2017,
.
::2017年6月5日编辑。 -
“Silo,” last edited May 11, 2017,
.
::2017年5月11日, -
“Great Pyramid of Giza,” last edited June 22, 2017,
.
::2017年6月22日编辑。 -
“Radius of the Planets - Universe Today,” by Abby Cessna, December 24, 2015,
.
::2015年12月24日 Abby Cessna所著的《行星的拉迪乌斯—今日宇宙》。
-
Triangle, 3 sides