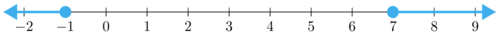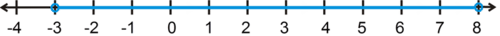2.10 解决绝对价值不平等

章节大纲

• 选择节常规

  折叠 展开

  常规

  全部折叠 展开全部

  • 选择活动新闻通告

    

    新闻通告 讨论区
• 选择节解决绝对价值不平等

  折叠 展开

  解决绝对价值不平等

  You are running errands during your lunch break. You have enough time to make a 3-mile round trip. Standing at an intersection , you can either go to the post office 2.3 miles to your right or the bank 1.2 miles to your left. Which errand should you run ?

  播放段落

  In this section, we consider problems like this in which a measurement falls inside or outside of a certain bound. 
  ::在本节中,我们考虑的问题类似于计量是否属于某一约束范围之内或之外的问题。

  

  播放段落

  Solving Absolute Value Inequalities
  ::解决绝对价值不平等

  播放段落

  Like absolute value equations, absolute value inequalities describe all of the values within or beyond a certain distance from a number on the number line. But whether or not the distance is within a certain bound or beyond it is a significant difference . Let's see how. 
  ::绝对值不平等与绝对值方程式一样,在数字线上,绝对值不平等可以描述数字线上与数字线上数字一定距离之内或之外的所有数值。但是,距离是否在某一约束之内或之外是一个显著的差别。让我们看看如何。

  播放段落

  by CK-12 demonstrates how to solve basic absolute value inequalities.  
  ::CK-12展示了如何解决基本绝对价值不平等问题。

    

  播放段落

  When we consider absolute value inequalities as greater than or less than , we are referring to whether the absolute value expression is greater than or less than the number.
  ::当我们认为绝对值不平等大于或小于或小于绝对值时,我们指的是绝对值表达面大于或小于数字。

  播放段落

  Solving Greater Than Inequalities
  ::解决大于不平等的不平等

  播放段落

  Example 1
  ::例1

  播放段落

  Solve and graph  $\begin{align*}|x|>1.\end{align*}$
  ::解析和图形 #% x # 1 。

  播放段落

  Solution: Let's first consider this inequality graphically. We want any number on the number line that is more than 1 unit from 0. On the right hand side, the lowest bound is 1, which is not included, and all of the numbers to the right are included. Remember solutions like 1.00000001 are included in the solution and need to be represented on the graph. Likewise, on the left hand side, the upper bound is -1 and it too is not included. All of the numbers to the left of -1 are in the solution set . Since 1 and -1 are not included, we will represent them on the graph with an open circle.
  ::解决方案 : 我们首先用图形方式来考虑这个不平等 。 我们想要数字线上的任何数字从 0 增加到 1 个单位。 在右手边, 最小的框是 1 个, 不包括其中, 所有数字都包含在右侧 。 记住解决方案中包含 100000001 这样的解决方案, 并且需要在图表中显示 。 同样, 在左手边, 上界是 - 1 , 也不包含它。 所有 - 1 左侧的数字都包含在解决方案中 。 由于1 和 - 1 不包含, 我们将以开放的圆在图表中代表它们 。

  

  播放段落

  Our solution is  $\begin{align*}(-\infty,-1) \cup (1,\infty)\end{align*}$ . 
  ::我们的解决方案是 (, -1)\\\\\1,\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\

  播放段落

  We can also consider this algebraically. Like absolute value equations, we have two possibilities. One is the interval on the right where the numbers are more than 1 unit to the right. The other is the interval on the left where the numbers are more than 1 unit to the left.
  ::我们也可以考虑这个代数。 和绝对值方程式一样, 我们有两种可能性。 一种是右边的间隔, 数字在右边超过1个单位。 另一种是左边的间隔, 数字在左边超过1个单位。

  播放段落

  $$\begin{align*}|x|&>1 \\ \swarrow &\searrow \\ \color{gray}{\text{remove from bars}} \qquad \color{black}{x>1} \ &\ \ x<-1 \qquad \color{gray}{\text{switch and negate}} \\\end{align*}$$
  ::\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\去去去去到\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\去去去去去去去去到\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\

  播放段落

  Notice in the second inequality, we did not write $\begin{align*}x>-1\end{align*}$ . This possibility represents what happens when the expression inside the absolute value bars is negative. In general, for the first solution, we leave the inequality sign the same and for the second solution we need to negate the number  AND switch the inequality sign. Also, note solutions to greater than inequalities are OR-type .
  ::在第二个不平等的警告中,我们没有写 x1。 这种可能性代表绝对值栏内表达为负值时发生的情况。 一般来说,对于第一个解决方案,我们让不平等的标志相同,对于我们需要否定数字和转换不平等标志的第二个解决方案,我们让不平等的标志相同。 另外,注意的比不平等更大的解决方案是或类型。

  播放段落

  Example 2
  ::例2

  播放段落

  Solve and graph  $\begin{align*}|x-3| \ge 4\end{align*}$ .
  ::解析和图表 *x-3*4。

  播放段落

  Solution:  Graphically, this inequality describes the distance between a number and 3, and that distance has to be more than 4 units or equal to 4 units. Our starting point is 3 and we have to consider numbers that are 4 units to the left  and right of 3. That is the minimum distance from 3. 
  ::解答: 图形化地说, 这种不平等描述数字与 3 之间的距离, 距离必须超过 4 个单位或等于 4 个单位。 我们的起点是 3 个, 我们必须从 3 个单位的左边和右边考虑 4 个单位。 这是 3 个单位的最小距离 。

  

  播放段落

  The solution is $\begin{align*}(-\infty, -1] \cup [7,\infty)\end{align*}$ . Algebraically, we have two possibilities—one where you take the inequality out of the absolute value bars (represents your solution to the left) and one where you take the inequality out of the absolute value bars, switch the direction of the inequality, and negate the number (represents your solution to the right).
  ::答案是 (, -1) , , , , 。 。 代数, 我们有两种可能性: 一种是您将不平等从绝对值栏中取出( 代表您对左边的解决方案) ,另一种是您将不平等从绝对值栏中取出, 改变不平等的方向, 否定数字( 代表您对右方的解决方案 ) 。

  播放段落

  $$\begin{align*}|x-&3| \ge 4 \\ \swarrow &\qquad \searrow \\ \color{gray}{\text{remove from bars}} \qquad \color{black}{x-3 \ge 4} &\qquad x-3 \le -4 \qquad \color{gray}{\text{switch and negate}}\\ \underline{\ +3 \ +3} &\qquad \ \underline{\ \ +3 \ \;\;+3} \\ x \ge 7 &\qquad x \le 4 \\\end{align*}$$
  ::X- 344444443333333333333333744

  播放段落

  Example 3 
  ::例3

  播放段落

  Solve and graph $\begin{align*}|4x-3|>9\end{align*}$ .
  ::解析和图表 #% 4x - 3\\\ 9 。

  播放段落

  Solution:  Like absolute value equations, it is sometimes easier to solve them algebraically. 
  ::解答:与绝对值方程式一样,有时比较容易代数解答。

  播放段落

  $$\begin{align*} & \qquad \ \ \ |4x-3|>9\\ & \qquad \qquad \swarrow \searrow\\ & 4x-3>9 \quad \ 4x-3<-9\\ & \quad \ \ 4x>12 \qquad \ 4x<-6\\ & \qquad x>3 \qquad \quad \ \ x<-\frac{3}{2}\end{align*}$$
  ::4x- 394x- 39 9 9 4x>12 4x6x3 x32

  播放段落

  The solution is  $\begin{align*}\bigg (-\infty, -\frac{3}{2} \bigg) \cup (3, \infty)\end{align*}$
  ::解决之道是 (,-32) (3,)

  播放段落

  The graph is:
  ::图表是:

  

  播放段落

  Solving Less Than Inequalities
  ::解决低于不平等的不平等

  播放段落

  Example 4
  ::例4

  播放段落

  Solve and graph  $\begin{align*}|x| \le 2\end{align*}$ . 
  ::解析和图解 x2。

  播放段落

  Solution:  Like greater than inequalities, we can think of this inequality graphically. We want numbers that are within 2 units of 0. 
  ::解决方案:与不平等相比,我们可以用图形来看待不平等。我们需要两个单位(0)内的数字。

  

  播放段落

  These are numbers between -2 and 2 or  $\begin{align*}[-2,2].\end{align*}$  
  ::这些数字介于-2至2或[-2、2]之间。

  播放段落

  If we solve this algebraically as we have done before, we get 
  ::如果我们像以前那样用代数解决这个代数,我们就会得到

  播放段落

  $$\begin{align*}|x| &\le 2 \\ \swarrow &\quad \searrow \\ \color{gray}{\text{remove from bars}} \qquad \color{black}{x \le 2} &\quad x \ge -2 \qquad \color{gray}{\text{switch and negate}}\\\end{align*}$$
  ::\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\去去去\\\\\\\\\\\\\\\\\\\\\\\去去去\\\\\\\\\\\\\\\\\\\\\去去去去去\\\\

  播放段落

  If we take all of the values in each inequality, we will get many "solutions" that do not satisfy the inequality. For example, $\begin{align*}-4 \le 2\end{align*}$ , so -4 is in the interval  $\begin{align*}(-\infty, 2]\end{align*}$ . However, $\begin{align*}|-4|=4 \nleq 2\end{align*}$ . Unlike greater than, solutions to less than inequalities are compound inequalities of the AND-type.  
  ::如果我们在每种不平等中都考虑到所有价值观, 我们就会得到许多无法满足不平等的“ 解决方案 ” 。 例如, 42, 所以 - 4是间隔期( 2) 。 然而, 4442 。 与更大的不同, 不平等程度低于不平等的解决方案是 和类型之间的多重不平等。

  播放段落

  $$\begin{align*}x \le 2 \quad &\text{and} \quad x \ge -2 \\ -2 \le &\ x \le 2 \end{align*}$$
  ::x% 2 和x% 2 - 2 × x% 2

  播放段落

  Example 5
  ::例5

  播放段落

  You are running errands during your lunch break. You have enough time to make a 3-mile round trip. Standing at an intersection, you can either go to the post office 2.3 miles to your right or the bank 1.2 miles to your left. Which errand should you run?
  ::您在午餐休息期间正在跑杂务。 您有足够的时间进行三英里的往返旅行。 站在十字路口, 您要么去邮局右侧2.3英里处, 要么去银行左侧1.2英里处。 您应该跑哪条路呢 ?

  播放段落

  Solution: You have enough time to make a 3-mile round trip, so you have enough time to go 1.5 miles in one direction and return to where you started. As an absolute value inequality, if we consider the intersection where you start to be position 0, we have  $\begin{align*}|x| \le 1.5\end{align*}$ . Solving this algebraically,
  ::解答:你有足够的时间进行三英里的往返旅行,所以你有足够的时间向一个方向走1.5英里,然后回到你开始的地方。作为一个绝对价值不平等,如果我们考虑到你开始处于0位置的交叉点,我们就有了x1.5。解决这个代数,

  播放段落

  $$\begin{align*}|x| &< 1.5\\ \swarrow &\qquad \searrow\\ x < 1.5 \quad &\text{and} \quad x > -1.5\\ \\ -1.5<&\ x<1.5 \end{align*}$$ And, graphically, we have
  ::===========================================================================================================================================================================================

    

  播放段落

  Since you can either go to the post office 2.3 miles to your right or the bank 1.2 miles to your left, you should go to the bank since 1.2 satisfies the inequality. 
  ::既然你既可以到邮局的右侧2.3英里处,也可以到银行的左侧1.2英里处,你应该去银行,因为1.2英里处满足了不平等。

  播放段落

  $$\begin{align*}& x=2.3: \ -1.5 \le 2.3 \nleq 1.5 \\ & x=1.2: \ -1.5 \le 1.2 \le 1.5 \\\end{align*}$$
  ::x=2.3:-1.5-2.3-1.5x=1.2:-1.5-1.2-1.5

  播放段落

  Example 6
  ::例6

  播放段落

  Solve and graph  $\begin{align*}|x+2| < 10\end{align*}$ .
  ::解析和图解 #% x+2\% 10 。

  播放段落

  Solution:  Graphically, if we want to think about this inequality in terms of distance, we need to rewrite inside the absolute value as subtraction :  $\begin{align*}|x+2|=|x-(-2)|\end{align*}$ . So, our starting point is -2 and we want to be within 10 units of it.
  ::解答:图形化地说,如果我们想从距离的角度来思考这种不平等,我们需要在绝对值内重写减号:x+2x-(-2)。因此,我们的起点是-2,我们想要在10个单位内重写。

  

  播放段落

  Algebraically, we proceed as follows
  ::代数,我们按以下顺序进行:

  播放段落

  $$\begin{align*}& \qquad \quad |x+2| < 10\\ & \qquad \qquad \swarrow \searrow\\ & x+2 < 10 \qquad x+2 > -10\\ & \ x < 8 \qquad \text{and} \qquad \ x > -12 \\ \\ & \qquad -12< \ x <8\end{align*}$$
  ::\ x+2\\\\\\\\\\\\ x+2 <10x+2\\\\\\ x8和 x12 -12 < x8

  播放段落

  Example 7
  ::例7

  播放段落

  Solve and graph  $\begin{align*}|-2x+5|<11\end{align*}$ .
  ::解析和图解 #% 2x+5+% 11 。

  播放段落

  Solution:   Considering this algebraically, we have
  ::解决方案:考虑到这个代数,我们

  播放段落

  $$\begin{align*}& \qquad \quad \ |-2x+5|<11\\ & \qquad \qquad \quad \ \ \swarrow \searrow\\ & -2x+5<11 \quad -2x+5>-11\\ & \quad \ \ -2x<6 \qquad \quad \ -2x>-16\\ & \qquad \quad \ x>-3 \qquad \qquad \ x<8\end{align*}$$
  ::@ 2x+5 @ 5 @ 11 @ 2x+5 < 11- 2x+5 @ 11- 2x < 6- 2x_ 16 x 3 x < 8

  播放段落

  The solution is $\begin{align*}x\end{align*}$ is greater than $\begin{align*}-3\end{align*}$ and less than $\begin{align*}8\end{align*}$ . In other words, the solution is $\begin{align*}-3 < x < 8\end{align*}$  or  $\begin{align*}(-3,8)\end{align*}$ . 
  ::溶液x大于-3,小于8。 换句话说,溶液为-3 < x < 8或(- 3,8)。

  播放段落

  The graph is:
  ::图表是:

  

   

  Less Than	Greater Than
  播放段落 If $\begin{align*}|ax+b| < c\end{align*}$ , then $\begin{align*}-c < ax+b < c\end{align*}$ . ::如果+ax+bc,则-c<ax+b>c。 播放段落 If $\begin{align*}|ax+b| \le c\end{align*}$ , then $\begin{align*}-c \le ax+b \le c\end{align*}$ . ::如果ax+bc,则-cx+bc。	播放段落 If $\begin{align*}|ax+b| > c\end{align*}$ , then $\begin{align*}ax+b<-c\end{align*}$ or $\begin{align*}ax+b>c\end{align*}$ . ::如果+ax+bc,则ax+bc或ax+b>c。 播放段落 If $\begin{align*}|ax+b| \ge c\end{align*}$ , then $\begin{align*}ax+b \le -c\end{align*}$ or $\begin{align*}ax+b \ge c\end{align*}$ . ::如果+ax+bc,则ax+bc或ax+bc。

  播放段落

  by CK-12 demonstrates how to solve absolute value inequalities. 
  ::CK-12展示了如何解决绝对价值不平等。

   

   

  播放段落

    How to Solve Absolute Value Inequalities With Desmos  
  ::如何解决绝对价值不平等与脱mos

  播放段落

  Enter each side of the equation into the utility as a function in the form y=_____. Then find the values of x where the absolute value graph (the V-shape) is above or below the horizontal line.
  ::将方程式的每个侧面输入到工具中,作为以 y 为形式的函数。然后在水平线以上或下方的绝对值图形( V- shape) 找到 x 的值 。

  播放段落

  Consider $\begin{align*}\left|x-2\right|\le 4\end{align*}$ .
  ::考虑一下x -2 -4

  播放段落
  1. Graph $\begin{align*}y = \left|x-2\right|\end{align*}$  and $\begin{align*}y=4\end{align*}$ .
     ::图 yx-2和y=4。
  播放段落
  2. The two graphs intersect at  $\begin{align*}x=-2\end{align*}$   and  $\begin{align*}x=6\end{align*}$  .The V-shape is below the horizontal line between those two values, so the solution is  $\begin{align*}[-2,6]\end{align*}$  .
     ::在 x2 和 x=6 上,两个图形相交。V 形状在这两个值之间的水平线下,所以答案是 [-2,6] 。

  播放段落

  We can use this graph to solve $\begin{align*}|x -2| \ge4\end{align*}$  as well. There are two intervals of x-values where the V-shape is above the horizontal line: $\begin{align*}(-\infty, -2] \cup [6, \infty)\end{align*}$ .
  ::也可以用此图解解析 x-24。 V- shape 位于水平线之上的 X 值间隔有两种 : (, − 2) [6, ] 。

  

  播放段落

  Special Cases
  ::特殊情况

  播放段落

  The solution set of an absolute value inequality is not always an interval. Consider the following examples.
  ::绝对价值不平等的一套解决办法并不总是一个间隔。 请参考以下例子 。

  播放段落

  Example 8
  ::例8

  播放段落

  Solve $\begin{align*}|x|<-4\end{align*}$ .
  ::解决4号房

  播放段落

  Solution: Since absolute value measures distance, it cannot be negative. There is no solution to this inequality.
  ::解决方案:由于绝对价值衡量距离,它不可能是负的,因此没有解决这种不平等的办法。

  播放段落

  Example 9
  ::例9

  播放段落

  Solve $\begin{align*}|x-7| \le 0\end{align*}$ . 
  ::解决x -7 -0。

  播放段落

  Solution: As we saw in the previous example, the left side of this inequality cannot be less than 0. However, it can be equal to 0. We have
  ::解决办法:正如我们在前一个例子中看到的那样,这种不平等的左面不能小于0。然而,它可以等于0。我们有。

  播放段落

  $$\begin{align*}|x-7|=0 \\ x-7 = 0 \\ x=7\end{align*}$$
  ::X - 70x - 7=0x=7

  播放段落

  So, there is only one solution here instead of an interval. 
  ::因此,这里只有一个解决办法,而不是一个间隔。

  播放段落

  Example 10
  ::例10

  播放段落

  Solve $\begin{align*}|x -3| \ge -5\end{align*}$ . 
  ::解决 #x - 3 # 5 。

  播放段落

  Solution: Absolute value will always be greater than or equal to 0, so every number is a solution here. The solution to this inequality is all real numbers. In interval notation, we have  $\begin{align*}\left({-\infty ,}{\infty }\right)\end{align*}$ .
  ::解决方案 : 绝对值总是大于或等于 0, 所以这里每个数字都是一个解决方案 。 解决这种不平等的方法都是真实数字 。 在间距符号中, 我们有 (,\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\"\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\

  播放段落

  Feature: Calibrating Units of Measure
  ::特征:测量单位校准单位

  播放段落

  by Tariq Ali
  ::塔里克·阿里(签名)

  播放段落

  Have you ever heard of a measurement "having an error of 3 percent"? Despite all efforts to make a measuring device accurate, there is a chance it will show results that are slightly incorrect. The difference, in terms of percentage error, is stated in the specifications of the device.
  ::是否听说过“ 误差为3% ” 的测量方法? 尽管为精确度测量设备付出了一切努力, 但它也有可能显示结果稍有误差。 在百分比误差方面, 差异在设备规格中注明 。

  播放段落

  What does a 3% error mean? It means that the absolute value of the difference between the measured and actual quantities is 3% of the actual value. You can use absolute value equations to calculate a range for it. Ideally, when a measuring device is manufactured, it is tested to ensure that it provides accurate results. For sophisticated equipment, this process is repeated periodically to ensure that any wear over time can be adjusted for appropriately. The pieces of equipment are then tuned so that they operate within the error again. This process is called calibration.
  ::3% 错误意味着什么 3% 错误? 这意味着测量数量和实际数量之间的绝对值是实际值的3%。 您可以使用绝对值方程来计算其范围。 理想的情况是, 当一个测量设备被制造出来时, 它会被测试以确保它提供准确的结果。 对于尖端设备, 此过程会定期重复, 以确保任何时间的磨损都能被适当调整。 然后对设备部件进行调整, 以便它们能在错误范围内再次运行。 这个过程被称为校准 。

  播放段落

  Consider the units of measure themselves. A pound is now officially defined in terms of kilograms, but what about the kilogram? Unlike the absolute definitions of second, meter, etc., the kilogram is the only standard unit that is defined by a physical object rather than a fundamental physical property . This artifact is called the International Prototype of the Kilogram (IPK), and it is held by the International Bureau of Weights and Measures, located in France. But unique problems can arise when the world relies on a particular object to define a unit. As it turned out a few years ago, the IPK is vulnerable to defects as well—the definition of kilogram needed some calibration!
  ::考虑测量单位本身。 一磅现在以公斤形式正式界定, 但公斤则如何? 与第二磅、 计量等的绝对定义不同, 公斤是唯一的标准单位, 由物理物体而不是基本物理财产来定义。 这个人工工艺品称为国际Kilquip(IPK)原型, 由设在法国的国际重力和计量局持有。 但是当世界依赖特定物体来定义一个单位时, 可能会出现独特的问题。 正如几年前所发现的那样, IPK很容易受到缺陷的影响, 以及需要校准的公斤定义 !

  播放段落

   by CK-12 shows how the world's roundest object helps solve the longest running problem in measurement - how to define the kilogram.  
  ::以 CK-12 显示世界圆圆对象如何帮助解决测量中最长的运行问题—— 如何定义千克。

    

  播放段落

  Summary
  ::摘要

  播放段落
  • You can solve absolute value inequalities graphically or algebraically.
    ::您可以用图形或代数来解析绝对值不平等。
  播放段落
  • To solve absolute value inequalities algebraically, consider two possibilities- one where you remove the absolute value bars and the other where you remove the absolute value bars, switch the direction of the inequality, and negate the number.
    ::解决绝对值不平等的代数,考虑两种可能性 -- -- 一种是删除绝对值条,另一种是删除绝对值条,改变不平等的方向,否定数字。
  播放段落
  • Less than inequalities have solutions of AND-type compound inequalities and greater than inequalities have solutions of OR-type compound inequalities.
    ::不平等程度低于不平等可解决的化合物不平等问题,而不平等程度大于不平等可解决的或类型化合物不平等问题。

  播放段落

  Review
  ::回顾

  播放段落

  Solve and graph the following absolute value inequalities.
  ::解决以下绝对价值不平等问题并绘制图表。

  播放段落
  1. $\begin{align*}|x| \ge 7\end{align*}$
     ::
  播放段落
  2. $\begin{align*}|x| < 16.32\end{align*}$
     ::16.32 16.32 16.32 16.32 16.32 16.32 16.32 16.32 16.32 16.32 16.32 16.32 16.32
  播放段落
  3. $\begin{align*}|-4x| > 3\end{align*}$
     ::{\fn华文楷体\fs16\1cHE0E0E0}*4x*3
  播放段落
  4. $\begin{align*}|x+6|>12\end{align*}$
     ::X+612
  播放段落
  5. $\begin{align*}|9-x| \le 16\end{align*}$
     ::9 -x16
  播放段落
  6. $\begin{align*}|2x-7| \ge 3\end{align*}$
     ::2x-73
  播放段落
  7. $\begin{align*}|8x-5|<27\end{align*}$
     ::8x-527
  播放段落
  8. $\begin{align*}\bigg | \frac{5}{6}x+1 \bigg |>6\end{align*}$
     ::56x+16
  播放段落
  9. $\begin{align*}|18-4x| \le 2\end{align*}$
     ::18 -4x2
  播放段落
  10. $\begin{align*}\bigg | \frac{3}{4}x-8 \bigg |>13\end{align*}$
      ::34x-813

  播放段落

  Explore More
  ::探索更多

  播放段落

  1. A cell tower transmits a signal to your device. To find the range of $\begin{align*}x\end{align*}$  over which you will not be able to connect to the cell tower, your phone or tablet would solve the following absolute value inequality: $\begin{align*}|x-500|>550\end{align*}$ . How far do you have to travel from the cell tower to be outside of its range?
  ::1. 电池塔将信号传送到设备上。要找到无法连接到电池塔的 x 范围,您的电话或平板电脑将解决以下绝对值不平等问题: x- 500 550。 您需要从该信号塔走多远才能超出其范围?

  播放段落

  2. Physicians say that a person’s body temperature should not exceed 0.5 degrees from 98.6 degrees Fahrenheit. ¹ Represent this relationship as an absolute value inequality, and then solve to know what the range of normal  body temperatures is.
  ::2. 医生说,一个人的体温不应超过98.6华氏度的0.5度。 1 将这种关系作为绝对值不平等来表示,然后解决了解正常体温的范围。

  播放段落

  3. In 2012, the Real Clear Politics average of national polls predicted that Barack Obama would win 48.8% of the vote with a margin of error of about 3%. What would be the range of percentages of the vote that Barack Obama could have received with a 3% margin of error? He received 51.1% of the votes. ² Was that within the margin of error? 
  ::3. 2012年,真正清晰的政治全国平均民意测验预测,巴拉克·奥巴马将赢得48.8%的选票,误差幅度约为3%。 巴拉克·奥巴马以误差幅度3%获得的选票的百分比范围会有多大? 他获得了51.1%的选票。 2 这是否在误差幅度之内?

  播放段落

  4. In June 2000, the Millennium Bridge, a pedestrian bridge to cross the River Thames, opened in London. It was quickly nicknamed the "Wobbly Bridge" because of the swaying motion of the bridge. It was quickly closed and remained closed for several years for repairs.
  ::4. 2000年6月,伦敦开通了穿越泰晤士河的行人桥千年桥,由于桥的摇摆动动动作,很快被命名为“沃布利桥”,并很快关闭并关闭了几年进行维修。

  播放段落

  Because of the swaying motion, people walked in step with the swaying and amplified the swaying motion further. For a lightweight bridge, like the Millennium Bridge, the lateral (sideways) vibration frequency should exceed 1.3 Hertz. ³ Write absolute value inequalities to represent the safe range of frequencies and the dangerous range.  
  ::由于摇摆运动,人们与摇摆运动步调一致,并放大了摇摆运动。 对于像千年桥(Millennium Bridge)这样的轻量级桥梁来说,平面(边缘)振动频率应该超过1.3赫兹。 3 写下绝对值不平等,以代表频率和危险射程的安全范围。

  播放段落

  Answers for Review and Explore More Problems
  ::回顾和探讨更多问题的答复

  播放段落

  Please see the Appendix. 
  ::请参看附录。

  播放段落

  References
  ::参考参考资料

  播放段落
  1. “Temperature - Clinical Methods - NCBI Bookshelf,” by Victor E. Del Bene, © 1990, Butterworth Publishers, a division of Reed Publishing, .
     ::Victor E. Del Bene著的“温度-临床方法-NCBI Bookshelf”,1990年,Butterworth出版社,Reed出版社司,......。
  播放段落
  2. “RealClearPolitics - Election 2012 - General Election: Romney vs. Obama,” .
     ::2012年大选:罗姆尼对奥巴马,
  播放段落
  3. “Millennium Bridge, London,” last updated June 26, 2017, .
     ::2017年6月26日更新。