3.5 在斜坡- 截取表中查找线的公式
章节大纲
-
You decide to buy a laptop for $800. Over time as the laptop is used, it loses value or depreciates. Say in 3 years, the laptop will be worth $450. If we assume linear depreciation, how much will the computer be worth after 6 years?
A linear equation that relates the two prices would help you determine how much the computer will be worth after 6 years. We consider one form of linear equations in this section.
::连接两种价格的线性方程将有助于您确定六年后计算机的价值。 我们在本节考虑一种线性方程形式。
Linear Equations of Two Variables
::两个变量的线性公式Linear equations of two variables share some properties with linear equations of one variable . The powers of each of the variables in a linear equation are all equal to 1. Also, the form of an equation of two variables is quite similar to the form of an equation of one variable, .
::两个变量的线性方程式与一个变量的线性方程式具有某些属性。线性方程式中每个变量的功率均等于 1. 另外,两个变量的方程式形式与一个变量的方程式形式(ax+b=c)相当相似。Linear Equations of Two Variables
::两个变量的线性公式A linear equation of two variables can be written:
::可以写入两个变量的线性方程式 :where a , b , and c are real numbers.
::ax+by=c,其中a、b和c为实际数字。Solutions to Equations With Two Variables
::具有两个变量的等式解决方案Solutions to equations of one variable are values that make the equation true. Similarly, solutions to equations with two variables are pairs of x- and y- values that make the equation true. There are an infinite number of possible combinations of x- and y- values that will satisfy the equation.
::一个变量的方程式的解决方案是使方程式成为真实的值。同样,两个变量的方程式的解决方案是使方程式成为真实的 x 和 Y 等值对等方。有无限数量的 x 和 y 等值组合可以满足方程式的要求。Example 1
::例1Determine if (1,2) is a solution to the equation .
::确定 y=x+1 的公式是否为 y=x+1 的解决方案(1, 2) 。Solution: As we will see in a moment, is an equation of a line in slope-intercept form . To show that (1,2) is a point on this line, we substitute 1 for and 2 for and determine if both sides are equal.
::解答: 正如我们将在一瞬间看到的那样, y=x+1 是斜坡截面线的方程式。 要显示( 1, 2) 是线上的一个点, 我们替换 x 1 和 2 y , 确定两边是否相等 。Since the pair (1,2) satisfies the equation, it is a solution.
::y=x+12=1+12=2 由于配对(1,2)满足方程,这是一个解决方案。Slope-Intercept Form
::斜坡- 截取窗体One way to describe the points on the line, or the solutions, is to use the and the y- coordinate of the y- intercept .
::描述线上各点或解决方案的一种方式是使用Y界面的Y界面和Y界面的坐标。Slope-Intercept Form of the Equation of a Line
::线条公式的斜坡截取形式The slope-intercept form of a line is:
::一条线的斜坡拦截形式是:
::y=mx+b y=mx+bwhere is the slope and is the y- coordinate of the y- intercept, the point where the line crosses the y- axis, the point .
::m 是斜坡, b 是 y 界面的 Y 坐标, 线横过 y 轴的点, 点 (0, b) 。Example 2
::例2The slope of a line is -4 and the y-intercept is (0, 3). What is the equation of the line?
::线的斜坡是 - 4, y 拦截是 (0, 3) 。 线的方程是多少 ?Solution: This problem explicitly tells us the slope and y- intercept. The slope is -4, meaning . The y- intercept is (0, 3), meaning . Therefore , the equation of the line is .
::解决方案 : 这个问题清楚地告诉我们斜坡和 y 界面。 斜坡是 4, 意思是 m4。 y 界面是 (0, 3), 意思是 b=3 。 因此, 线的方程式是 y4x+3 。by CK-12 demonstrates how to write equations in slope-intercept form given the slope and y -intercept.
::通过 CK-12 演示如何根据斜坡和 y 界面以斜坡界面的形式写出方程式 。Example 3
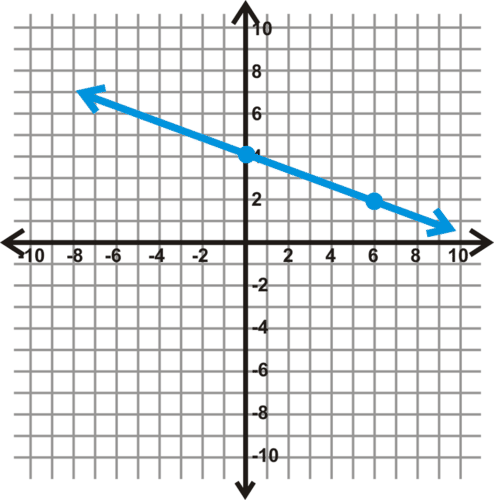
::例3Find the equation of the line below.
::查找下方线的方程式 。Solution: From the graph, it looks like the line passes through the y- axis at (0, 4), making . Now, we need to find the slope. You can use rise over run or the slope formula . Using the slope formula, we assign and . So,
::解析方式 : 从图表看, 线条似乎是在 y 轴 值 (0, 4) 处通过 y 轴, 制成 b= 4。 现在, 我们需要找到斜坡 。 您可以使用 向上 或 斜坡 公式 。 使用 斜坡 公式, 我们分配 (x1, y1) = (0, 4) 和 (x2, y2) = (6, 2) 。 所以,
::m=2-46-02613Substituting the information we found into the slope-intercept equation, the equation that describes the points on this line is .
::将我们发现的信息 替换为斜坡界面方程式, 描述此线各点的方程式是 y13x+4 。by CK-12 demonstrates how to write the slope-intercept equation for a line given the graph of the line.
::通过 CK-12 演示如何为线条的图形绘制线条的斜度截面方程式 。Example 4
::例4The slope of a line is and it passes through the point (4, -7). What is the equation of the line?
::线的斜坡是12, 穿过点( 4, - 7) 。 线的方程是多少 ?Solution: In this problem, we are given and a point on the line. The point, (4, -7) can be substituted in for and in the slope-intercept form of an equation to solve for the y- intercept, or . Substituting in what we know into the slope-intercept equation
::解决方案 : 在此问题上, 我们得到 m 和线上的一个点 。 点 (4, - 7) 可以替换为 x 和 y , 以斜度截取方程式的 斜度方程式 解决 y 截取, 或 b 。 将我们所知道的东西替换为斜度截取方程式
::y=mx+b-7=12(4)+b-7=2+b-9=bWe see that the equation of the line is .
::我们看到线的方程式是 Y=12x- 9 。Example 5
::例5You decide to buy a laptop for $800. I n 3 years, the laptop will be worth $450. Write an equation of the line that describes the value of the laptop computer. H ow much will the computer be worth after 6 years?
::您决定以800美元购买一台笔记本电脑。 3年后, 笔记本电脑将值450美元。 写出描述笔记本电脑价值的线条方程式。 6年后电脑值多少?Solution: To determine the equation of the line, rewrite the given information as points. The first could be (0, 800) since at time 0 years you buy the computer for $800. The second would be (3, 450) since the value of the computer after 3 years is $450. Since one of the points is the y- intercept, we just need to f ind the slope. Set and .
::解决方案 : 要确定线条的方程, 请将给定信息重写为点 。 第一个可能是( 0, 800) 。 第一个可能是( 0, 800 ) , 因为您在时间 0 时购买电脑800 美元。 第二个是 ( 3, 450 ) , 因为3 年后计算机的价值是 450 美元。 由于其中一个点是 y 接口, 我们只需要找到斜坡 。 Set (x1,y1) = (3,450) 和 (x2,y2) = (0,800) 。
::my2-y1x2-x1=800-4500-333503Therefore, the equation of the declining value of the laptop is . In 6 years or , the laptop will be worth or $100.
::因此,膝上型计算机价值下降的方程式是y3503x+800。在6年或x=6中,膝上型计算机的价值将为y3503}6+800700+800=100或100美元。by CK-12 demonstrates how to write equations in slope-intercept form given two points on the graph.
::通过 CK-12 演示如何在图形上两点的情况下以斜度截取形式写出方程式 。Example 6
::例6Find the equation of the line that passes through (12, 7) and (10, -1).
::查找通过(12、7)和(10、-1)的线条的方程。Solution: In this example, we are not given the slope or the y- intercept. First, let's find the slope. Set and .
::解决方案 : 在此示例中, 我们没有给出斜坡或 Y 界面 。 首先, 让我们找到斜坡 。 Set (x1, y1) = (12, 7) 和 (x2, y2) = (10, - 1) 。
::1 - 710 - 128 - 2=4Now, as we did in Example 4, plug in one of the points for and to find . It does not matter which point you choose because they are both on the line or solutions to the equation.
::现在,正如我们在例4中所做的那样, 插入 x 和 y 找到 b 的点之一。 您选择哪个点并不重要, 因为它们都位于等式的线上或解决方案上 。
::7=4(12)+B7=48+b-41=bThe equation of the line is .
::线的方程式是y=4x-41。Summary
::摘要-
To write the equation of a line in slope-intercept form,
, identify the slope,
, and the
intercept,
, and substitute for
and
.
::以斜坡截面格式写出线的方程式,y=mx+b,标明斜坡、m和y-截面(0,b),并替换m和b。
Review
::回顾Find the equation of each line with the given information below.
::以下文提供的信息查找每行的方程。-
slope = 2,
y-
intercept = (0, 3)
::斜坡 = 2, y- 界面 = (0, 3) -
::m14, b=2.6 -
x-
intercept = (-2, 0),
y-
intercept = (0, -5)
::x 截取 = (-2, 0, y- 截取 = (0, 5) -
slope = 1 and passes through (2, 4)
::斜坡=1,通过(2,4) -
slope
and passes through (-2, 5)
::斜度 34 并通过 (-2, 5) -
passes through (-5, 4) and (1, 1)
::通过(5、4和1、1和1) -
passes through (5, -1) and (-10, -10)
::通过(5,-1)和(10,-10)
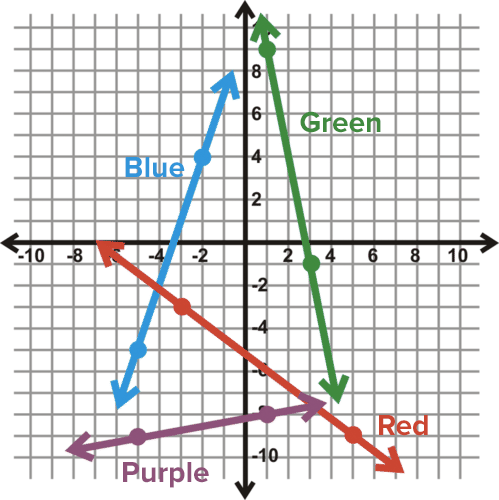
For problems 8-11, find the equation of the lines in the graph below.
::对于问题8-11,请在下图中找到行的方程式。-
Green Line
::绿线 -
Blue Line
::" 蓝线 " 蓝线 -
Red Line
::红线 -
Purple Line
::紫线
Explore More
::探索更多1. a. Find the equation of the line with zero slope and passes through the point (-4, 5).
::1.a. 确定线的方程式为零斜度,穿过点(-4、5)。b. Find the equation of the line with zero slope and passes through the point .
::b. 查找线的方程式为零斜度,穿过点(a,b)。2. A business purchases a photocopier for $2,989.45. Write an equation to model the value of the photocopier over a period of 5 years if the business uses straight-line depreciation as in Example 5.
::2. 企业购买一台复印机2,989.45美元;如果企业使用例5中的直线折旧法,则写一个方程式,在5年内模拟复印机的价值。3. The cost of producing a college textbook is $140.55 per book. Write an equation to model the costs for the publisher to produce number of books. 1
::3. 编制大学教科书的费用为每本书140.55美元,编写一个方程式,作为出版商制作x册书籍的费用的模型。
::4. 在物理学中,可使用公式 vf=vi+at确定一个物体在自由坠落时的速度(或速度),该公式的 vf=vi+at 是最终速度, vf 是初始速度, vi 是重力加速速度, a 是重力加速速度, t 是时间。
::Evel Knievel是一个摩托车特技演员,他声称他可以骑摩托车穿越大峡谷,他认为他的摩托车加上一些喷气背包,可以达到每小时250英里的最初速度。 2 如果重力加速速度为21.937米/秒,请写一个方程来模拟这种情况。在他最后速度为0英里之前,他能在空中停留几秒钟?5. The percent of cellphone-only households has increased steadily over the past 13 years. If 3 percent of households in 2003 were cellphone-only households and 32.3 percent were cellphone-only in 2012, how can this data be modeled with a linear equation in slope-intercept form? 3 Use this model to predict the number of households that will be cellphone-only households in 2017.
::5. 过去13年来,只用手机的家庭比例稳步上升,如果2003年3%的家庭是只用手机的家庭,而2012年32.3%的家庭是只用手机的家庭,那么,如何用斜坡拦截形式的线性方程式模拟这一数据?3 利用这一模式预测2017年将使用手机的家庭数量。Answers to Review and Explore More Problems
::对审查和探讨更多问题的答复Please see the Appendix.
::请参看附录。PLIX
::PLIXTry this interactive that reinforces the concepts explored in this section:
::尝试这一互动,强化本节所探讨的概念:References
::参考参考资料-
“Why Are Textbooks So Expensive?,” by Zachary Crockett, published December 18, 2013,
.
::作者Zachary Crockett在2013年12月18日发表。 -
“Evel Knievel | Triumph Over the Fountains at Caesars Palace - The Selvedge Yard,” posted October 16, 2012,
.
::2012年10月16日张贴的《凯撒宫不老泉的胜利-塞维奇场》。 -
“Behavioral Risk Factor Surveillance System (BRFSS) Methodology,” last updated 2015,
.
::“行为风险因素监测系统(BRFSS)方法”,最近一次更新的2015年,......。
-
To write the equation of a line in slope-intercept form,
, identify the slope,
, and the
intercept,
, and substitute for
and
.