4.3 通过图表绘制的平方溶解系统

Section outline

• Select section General

  Collapse Expand

  General

  Collapse all Expand all

  • Select activity 新闻通告

    

    新闻通告 Forum
• Select section 通过图表绘制的平方解决系统

  Collapse Expand

  通过图表绘制的平方解决系统

  播放段落

  Many of the streets in Manhattan are organized as a grid. Numbered streets are east-west, and numbered and named avenues run north-south. Therefore , we can consider the streets as horizontal lines and the avenues as vertical lines. Using this convention,  $\begin{array}{r}y=34\end{array}$  would represent 34 ^th  Street and $\begin{array}{r}x=6\end{array}$  would represent 6 ^th Avenue. We could find the solution to these two equations by graphing the lines and determining where they intersect.
  
  ::曼哈顿的许多街道都是以网格形式组织起来的。 数字街道是东西方的, 编号和命名的街道是南北方的。 因此, 我们可以将街道视为横向线, 将通道视为垂直线。 使用这个会议, y=34将代表34街, x=6将代表第六大道。 我们可以通过绘制线条图并确定其交叉之处, 找到这两个方程式的解决方案 。

  播放段落

  In this section, we consider problems like this by graphing.
  ::在本节中,我们通过图解来考虑这类问题。

  

  播放段落

  Graphing Linear Systems of Equations
  ::平面线条系统

  播放段落

  One way to determine the solution(s) to a system of equations is to graph the pairs of lines in systems of linear equations and identify the point(s) of intersection . Let's consider some systems of equations below.
  ::确定方程系统解决方案的一个方法就是用线性方程系统绘制线条对数图,并确定交叉点。让我们来考虑下面的一些方程系统。

  播放段落

  Example 1
  ::例1

  播放段落

  Graph and solve the system:
  ::图形和解析系统 :

  播放段落

  $$\begin{array}{r}3x+2y=6\\ y=-\frac{1}{2}x-1\end{array}$$

  
  ::3x+2y=6y12x-1

  播放段落

  Solution: For the first equation , we can either solve for $\begin{array}{r}y\end{array}$ to put it in slope-intercept form or we can use the intercepts to graph the equation. To review using intercepts to graph lines, we will use the latter method.
  ::解答: 对于第一个方程式, 我们要么解决 y 将其以斜坡截取形式放置, 要么我们用拦截来绘制方程式的图解。 要用拦截来查看图形线, 我们将使用后一种方法 。

  播放段落

  Recall that the x- intercept can be found by replacing $\begin{array}{r}y\end{array}$ with zero and solving for $\begin{array}{r}x\end{array}$ :
  ::回顾 X 界面可以用零替换 Y 和解析 x 找到 :

  播放段落

  $$\begin{array}{rl}3x+2(0)& =6\\ 3x& =6\\ x& =2\end{array}$$

  
  ::3x+2(0)=63x=6x=2

  播放段落

  Similarly, the y- intercept is found by replacing $\begin{array}{r}x\end{array}$ with zero and solving for $\begin{array}{r}y\end{array}$ :
  ::同样, Y 界面通过将x 替换为 0 和 y 的溶解 来找到 y 界面 :

  播放段落

  $$\begin{array}{rl}3(0)+2y& =6\\ 2y& =6\\ y& =3\end{array}$$

  
  ::3(0)+2y=62y=6y=3

  播放段落

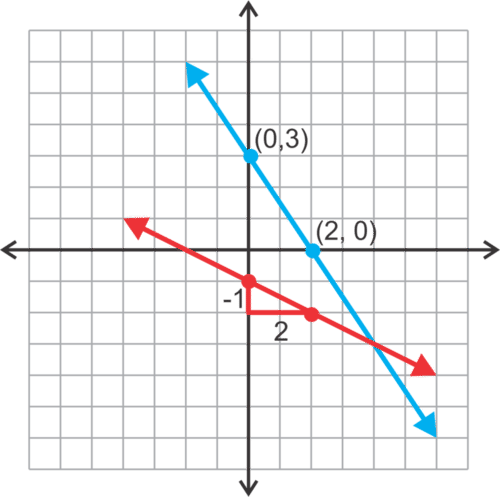
  We have two points, (2, 0) and (0, 3) to plot and graph this line.
  ::我们有两个点, (2, 0) 和 (0, 3) 来绘制和绘制此行的图表 。

  播放段落

  Equation 2 can be graphed using the y- intercept and .
  ::方程式 2 可以用 y 界面和 。

  

  播放段落

  Now that both lines are graphed we observe that their intersection is the point (4, -3).
  ::现在两条线都用图表标示了 我们观察到它们的交叉点是点 (4, - 3) 。

  播放段落

  Finally, check this solution by substituting it into each of the two equations.
  ::最后,检查这一解决方案,将其替换为两个方程式中的每一个方程式。

  播放段落

  Equation 1:
  ::等式 1 :

  播放段落

  $$\begin{array}{rl}3x+2y& =6\\ 3(4)+2(-3)& =6\\ 6& =6\end{array}$$

        
  ::3x+2y=63(4)+2(-3)=66=6

  播放段落

  Equation 2:
  ::等式 2 :

  播放段落

  $$\begin{array}{rl}y& =-\frac{1}{2}x-1\\ -3& =-\frac{1}{2}(4)-1\\ -3& =-2-1\\ -3& =-3\end{array}$$

  
  ::y12x - 1 - 312(4) - 1 - 32 - 1 - 33

  播放段落

  by CK-12 demonstrates the fundamental characteristics of linear systems. 
  ::CK-12表明线性系统的基本特征。

  播放段落

  Example 2
  ::例2

  播放段落

  Solve the following system by graphing.
  
  ::通过图表绘制解决以下系统 。

  播放段落

  $$\begin{array}{rl}y& =3x-4\\ y& =2\end{array}$$

  
  ::y=3x-4y=2

  播放段落

  Solution: The first line is in slope-intercept form and can be graphed accordingly. The second line is a horizontal line through (0, 2). The graph of the two equations is shown below.
  ::解析度:第一行以斜坡截面形式,可按下图绘制。第二行是横直线通过(0, 2),两个方程式的图如下。

  

  播放段落

  From this graph the solution appears to be (2, 2). Checking this solution in each equation verifies that it is indeed correct.
  ::从这个图表看,解决办法似乎是(2,2),在每个方程式中检查这一解决办法,可以核实它是否确实正确。

  播放段落

  Equation 1:
  ::等式 1 :

  $$\begin{array}{rl}2& =3(2)-4\\ 2& =6-4\\ 2& =2\end{array}$$

          

  播放段落

  Equation 2:
  ::等式 2 :

  $$\begin{array}{r}2=2\end{array}$$

  播放段落

  Example 3
  ::例3

  播放段落

  Solve the following system of equations by graphing.
  ::通过图形化解决以下方程式系统。

  播放段落

  $$\begin{array}{r}y=-\frac{3}{2}x-1\\ 3x+2y=-2\end{array}$$

  
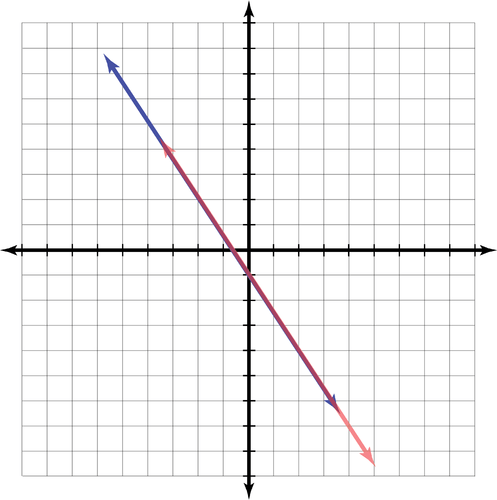
  ::y32x- 13x+2y @% 2

  播放段落

  Solution: When we graph the system of equations, we get the graph below. These two lines are the same line.
  ::解答: 当我们绘制方程式系统图时, 我们可以看到下面的图。 这两个线线是相同的线 。

  

  播放段落

  So, every point on these lines is a solution to the system of equations. For example, (-2, 2) is a point on the line. It is a solution to both equations as seen below. 
  ::因此,这些线条上的每一个点都是方程体系的解决方案。例如,( 2) 2 是线上的一个点。它是下文所看到的两种方程的解决方案。

  $$\begin{array}{r}2=-\frac{3}{2}(-2)-1⟶2=3-1⟶2=2\\ \\ 3(-2)+2(2)=-2⟶-6+4=-2⟶-2=-2\end{array}$$

  播放段落

  by MyWhyU  explains how the points of intersection of two graphs represent common solutions of both equation. It shows how finding these intersection points is an important tool in analyzing physical and mathematical systems.
  ::由 MyHauseU 解释两个图形的交叉点如何代表两个方程式的共同解决方案。 它显示找到这些交叉点是如何分析物理和数学系统的一个重要工具。

  播放段落

  Graphing is not always the best method for solving a system of equations. For example, if you graph the system below, you get the following graph.
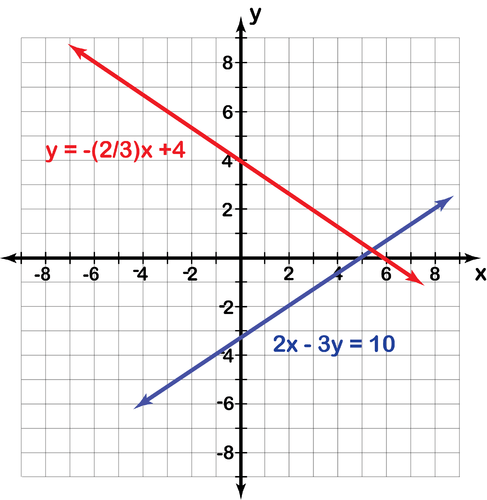
  ::绘图并不总是解决方程式系统的最佳方法。例如,如果您在下面绘制系统图,您可以得到下图。

  播放段落

  $$\begin{array}{rl}2x-3y& =10\\ y& =-\frac{2}{3}x+4\end{array}$$

  
  ::2 - 3y=10y23x+4

  播放段落

  The first equation,   $\begin{array}{r}y=\frac{2}{3}x-\frac{10}{3}\end{array}$ , is graphed in blue . The second equation, $\begin{array}{r}y=-\frac{2}{3}+4\end{array}$ , is graphed in   red .
  

  
  ::第一个方程式 y= 23x- 103 以蓝色图解。第二个方程式 y= 23+ 4 以红色图解 。

  播放段落

  While you can approximate the solution to this system, you cannot say exactly where the intersection point is since it does not fall on integer values on the number lines. Even if a point on a graph appears to be the solution to a system, you always need to check your solution algebraically. You can also solve a system like this with a graphing utility.
  ::虽然您可以接近此系统的解决方案,但您无法确切指出交叉点的确切位置,因为它不落在数字行的整数值上。即使图形上的某个点似乎是系统的解决方案,您也总是需要检查您的解决方案代数。您也可以使用图形化工具解析这样的系统。

  播放段落

   Solving a System of Equations Using  Desmos
  ::解决使用desmos的等同系统

  播放段落

  Let's consider the system of equations above. 
  ::让我们考虑一下上面的方程式

  播放段落

  1. Graph these equations in the utility. The first equation must be rearranged into slope-intercept form.
  ::1. 在工具中绘制这些方程图。第一个方程必须重新排列为斜坡界面形式。

  播放段落

  $$\begin{array}{rl}2x-3y& =10\\ -3y& =-2x+10\\ y& =\frac{-2x+10}{-3}\\ y& =\frac{2}{3}x-\frac{10}{3}\end{array}$$

  
  ::2 - 3y=10 - 3y2x+10y2x+10-3y=23x- 103

  播放段落

  With Desmos, you can click on the intersection point to get the coordinates .
  ::与德摩斯,你可以点击交叉点 获得坐标。

  

  播放段落

  WARNINGS
  ::警告

  播放段落

  1. In Desmos, click on the wrench icon in the upper-right and change the values for the x -axis and the y -axis.
  ::1. 在德摩斯,单击右上角的扳手图标,并更改x轴和y轴的值。

  播放段落

  2. Lines with slopes that are close in value may look like they will never intersect in a graphing utility. However, if the slopes of the lines are different, the lines will intersect.
  ::2. 斜坡值接近的线形看似在图形工具中永远不会交叉,但是,如果线形的斜坡不同,线形就会交叉。

  播放段落

     Solving a System of Equations Using a TI-83/84
  ::利用TI-83/84解决等同系统

  播放段落

  1. Graph these equations in the utility. The first equation must be rearranged into slope-intercept form.
  ::1. 在工具中绘制这些方程图。第一个方程必须重新排列为斜坡界面形式。

  播放段落

  $$\begin{array}{rl}2x-3y& =10\\ -3y& =-2x+10\\ y& =\frac{-2x+10}{-3}\\ y& =\frac{2}{3}x-\frac{10}{3}\end{array}$$

  
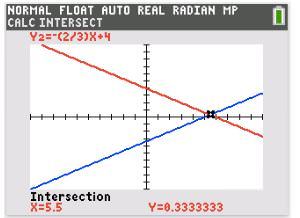
  ::2 - 3y=10 - 3y2x+10y2x+10-3y=23x- 103

  播放段落

  2. If you have a TI-83 or 84, use the CALC menu, select INTERSECT . Then select each line by pressing ENTER on each one. The calculator will give you a “guess.” Press ENTER one more time and the calculator will then calculate the intersection of (5.5, .333...). We can also write this point as $\begin{array}{r}\left(\frac{11}{2},\frac{1}{3}\right)\end{array}$ . Check the solution algebraically.
  ::2. 如果您有一个 TI-83 或 84, 请使用 CALC 菜单, 选择 InterSECT 。 然后按 ENTER 键选择每条线。 计算器会给你一个“ 猜测 ” 。 按 ENTER 一次, 然后计算器将计算( 5. 5 , 333...) 的交叉点。 我们也可以将此点写为 (112, 13) 。 请检查解答代数 。

  

  播放段落

  WARNINGS
  ::警告

  播放段落

  1. If the two lines do not intersect, you may need to adjust the viewing window. On a graphing calculator, change the WINDOW settings or ZOOM settings.
  ::1. 如果两行不交叉,您可能需要调整查看窗口。在图形计算器上,更改 WINDOW 设置或 ZOOM 设置。

  播放段落

  2. Lines with slopes that are close in value may look like they will never intersect in a graphing utility. However, if the slopes of the lines are different, the lines will intersect.
  ::2. 斜坡值接近的线形看似在图形工具中永远不会交叉,但是,如果线形的斜坡不同,线形就会交叉。

  播放段落

  
  Summary
  ::摘要

  播放段落
  • Graph the lines together on the same set of axes. The solution(s) is (are) any points of intersection.
    ::在同一组轴上共同绘制线条图。解决方案是(指)任何交叉点。

  播放段落

  Review
  ::回顾

  播放段落

  Match the system of linear equations to its graph and state the solution.
  ::将线性方程系统与其图形匹配,并声明解决方案。

  播放段落

  1.   $\begin{array}{r}\begin{array}{rl}3x+2y& =-2\\ x-y& =-4\end{array}\end{array}$
  ::1. 3x+2y2x-y4

  播放段落

  a.                                                                           
  ::a 。

  

  播放段落

  b.
  ::b. b. 数据

   

  播放段落

  c.                                                                            
  ::c. 用于以下目的:

  

  播放段落

  d.
  ::d. 数据

   

  播放段落

  2.   $\begin{array}{r}\begin{array}{rl}2x-y& =6\\ 2x+3y& =6\end{array}\end{array}$
  ::2. 2x-y=62x+3y=6

  播放段落

  a.                                                             
  ::a 。

  

        

  播放段落

  b.
  ::b. b. 数据

  

  播放段落

  c.
  ::c. 用于以下目的:

  

  播放段落

  d.
  ::d. 数据

  

  播放段落

  3. $\begin{array}{r}\begin{array}{rl}2x-5y& =-5\\ x+5y& =5\end{array}\end{array}$
  ::3. 2x-5y5x+5y=5

  播放段落

  a.
  
  ::a 。

  

         

  播放段落

  b.
  ::b. b. 数据

  

            

  播放段落

  c.
  
  ::c. 用于以下目的:

  

  播放段落

  d.
  ::d. 数据

  

                                                             

  播放段落

  4.  $\begin{array}{r}\begin{array}{rl}y& =5x-5\\ y& =-x+1\end{array}\end{array}$
  ::4. y=5x-5yx+1

  播放段落

  a.                                                                      
  
  ::a 。

  

  播放段落

  b.
  ::b. b. 数据

  

   

  播放段落

  c.
  ::c. 用于以下目的:

  

  播放段落

  d.
  ::d. 数据

  

  播放段落

  Solve the following linear systems by graphing. Use graph paper and a straightedge to ensure accuracy. Check all of your solutions  algebraically.
  ::通过图形化来解决下列线性系统。使用图形纸和直方以确保准确性。检查所有溶液的代数。

  播放段落

  5.   $\begin{array}{r}y=-\frac{2}{5}x+1\\ y=\frac{3}{5}x-4\end{array}$    
  ::5. y25x+1y=35x-4

  播放段落

  6.  $\begin{array}{r}y=-\frac{2}{3}x+4\\ y=3x-7\end{array}$
  ::6. y23x+4y=3x-7

  播放段落

  7.  $\begin{array}{r}y=-2x+1\\ x-y=-4\end{array}$
  ::7. y2x+1x-y4

  播放段落

  8.  $\begin{array}{r}3x+4y=12\\ x-4y=4\end{array}$
  ::8. 3x+4y=12x-4y=4

  播放段落

  9.  $\begin{array}{r}7x-2y=-4\\ y=-5\end{array}$
  ::9. 7x-2y___________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

  播放段落

  10.  $\begin{array}{r}x-2y=-8\\ x=-3\end{array}$
  ::10 - 2y8x3

  播放段落

  Explore More
  ::探索更多

  播放段落

  1. Clara and her brother, Carl, are at the beach for vacation. They want to rent bikes to ride up and down the boardwalk. One rental shop, Bargain Bikes, advertises rates of $5 plus $1.50 per hour. A second shop, Frugal Wheels, advertises a rate of $6 plus $1.25 an hour.
  ::1. 克拉拉和她的兄弟卡尔在海滩度假,他们想租自行车上下上下上下上下上下上下上下上下上下上下上下上下上下上下上下上下上下上下上下下上下下上下下上下下上下下上下下上下下上下下下上下下上下下下上下下下下上下下下下上下下下下上下下下下下下上下下下下下上下下下下下下下下上下下下下上下下下下下下下下下下上下下下下下上下下下下下上下下下下下下下下下下下下下下下下下下下下下下下下下下下下下下下下下下下。一个出租店是Bargleg Bikes,广告上下下下下下下下下下下下下下下下下下下下下下下下下下下下下下下下下下下下下下下下下下为5美元。第二间铺铺铺铺铺铺铺铺铺铺铺铺,每小时5美元加1.50美元。

  播放段落

  a. How much does it cost to rent a bike for one hour from each shop? How about 10 hours?
  ::a. 从每个商店租用一辆单车一小时需要多少钱?

  播放段落

  b. Write equations to represent the cost of renting a bike from each shop. Let $\begin{array}{r}x\end{array}$  represent the number of hours and $\begin{array}{r}y\end{array}$  represent the total cost.
  ::b. 写公式,以表示从每个商店租用自行车的费用。

  播放段落

  c. Solve your system to figure out when the cost is the same.
  ::c. 解决你的系统,以找出成本何时相同。

  播放段落

  d. Clara and Carl want to rent the bikes for about 3 hours. Which shop should they use?
  ::d. 克拉拉和卡尔想租三小时左右的自行车,他们应该用哪家店?

  播放段落

  2. Peter and Nadia like to race each other. Peter can run at a speed of 5 feet per second and Nadia can run at a speed of 6 feet per second. To be a good sport, Nadia likes to give Peter a head start of 20 feet. How long does Nadia take to catch up with Peter? At what distance from the start does Nadia catch up with Peter?
  ::2. Peter和Nadia喜欢相互竞争:Peter每秒跑5英尺,Nadia每秒跑6英尺;为好运动,Nadia喜欢让Peter先跑20英尺;Nadia要多久才能赶上Peter?Nadia从什么时候开始追上Peter?

  播放段落

  3. Mary’s car is 10 years old and has a problem. The repair man indicates that it will cost her $1,200.00 to repair her car. She can purchase a different, more efficient car for $4,500.00. Her present car averages about $2,000.00 per year for gas while the new car would average about $1,500.00 per year. Find the number of years for which the total cost of repairs would equal the total cost of replacement.
  ::3. Mary的汽车10岁,有问题:修理工表示,修理她的汽车需要花费1 200美元,她可以购买另外的、效率更高的汽车,费用为4 500美元;她现在的汽车汽油每年平均大约2 000.00美元,而新车每年平均大约1 500美元;查明修理总费用与更换总费用相等的年数。

  播放段落

  4. Juan is considering two cell phone plans. The first company charges $120.00 for the phone and $30 per month for the calling plan that Juan wants. The second company charges $40.00 for the same phone, but charges $45 per month for the calling plan that Juan wants. After how many months would the total cost of the two plans be the same?
  ::4. 胡安正在考虑两个手机计划:第一家公司为胡安想要的电话收费120美元,每月30美元;第二家公司为同一电话收费40.00美元,但为胡安想要的电话计划每月收费45美元。

  播放段落

  Answers for Review and Explore More Problems
  ::回顾和探讨更多问题的答复

  播放段落

  Please see Appendix.
  ::请见附录。

  播放段落

  PLIX
  ::PLIX

  播放段落

  Try this interactive that reinforces the concepts explored in this section:
  ::尝试这一互动,强化本节所探讨的概念: