Course: 4.7 确定解决等分系统时采用的最佳方法

Section outline

Select section General

Collapse Expand
General

Collapse all Expand all
- Select activity 新闻通告
  
  新闻通告 Forum
Select section 确定解决公平体系时采用的最佳方法

Collapse Expand
确定解决公平体系时采用的最佳方法
A rental car company, Affordable Autos, charges $30 per day plus $0.51 per mile driven. A second car rental company, Cheap Cars, charges $25 per day plus $0.57 per mile driven. For a short distance , Cheap Cars offers the better deal. At what point (after how many miles in a single day) does the Affordable Autos rental company offer the better deal?
::第二家汽车租赁公司,廉价汽车,每天25美元,每英里0.57美元。短期而言,廉价汽车提供了更好的交易。廉价汽车租赁公司在什么时候(在一天里多英里之后 ) 提供了更好的交易?

What Is the Best Method?
::什么是最佳方法?

Any of the methods—graphing, substitution, or elimination by addition—learned in this unit can be used to solve a system of linear equations. Sometimes, however, it is more efficient to use one method over another based on how the equations are presented. Let's look at the pros and cons of each.
::任何方法——绘图、替代或通过添加消除——都可以用来解决线性方程式系统的问题,但有时,根据方程式的表述方式,使用一种方法比另一种方法更有效,让我们审视一下每个方程式的利弊。

Graphing
::图表绘制

Graphing is good to use if you have to answer many questions or see the trends of the data in the system. If you have access to a graphing program or calculator, it is also probably the easiest method to use.
::如果您必须回答许多问题或看到系统中数据的趋势, 使用图形是很好的。如果您可以访问图形程序或计算器, 这可能是最容易使用的方法。

If you are graphing by hand, one of the pitfalls of graphing a system is if the solution includes a coordinate that is not an integer . It is hard to judge the exact values by graphing. Therefore , graphing by hand can be imprecise and error-prone. Also, when using graphing you must always check your solution algebraically. Therefore, using graphing may take more time than the other methods.
::如果您是用手绘制图表, 系统图形的一个陷阱就是如果解决方案包含一个不是整数的坐标。很难通过图形来判断准确值。因此, 手绘制图形可能不准确, 且容易出错。另外, 在使用图形时, 您必须检查您的解决方案的代数。因此, 使用图形可能比其他方法花费更多时间。

Example 1
::例1

The number of students that attend two tutoring sessions can be modeled by the following equations where x is the week in the semester and y is the number of students that attend . In what week are the same number of students attending each session?
::参加两次辅导课程的学生人数可以用下列方程式来模拟:学期x是学期的周,y是参加的学生人数。在哪个星期参加每次课程的学生人数相同?

$\begin{aligned} y & = - x + 5 \\ y & = \frac{1}{2} x + 2 \end{aligned}$
$\begin{align*}y &= -x+5\\ y &= \frac{1}{2}x+2\end{align*}$
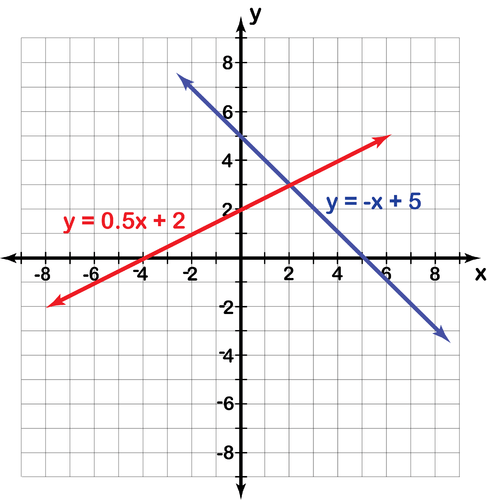
::yux+5y=12x+2

Solution: Since both equations are in slope-intercept form , we could graph these lines. The question is whether or not the intersection of the two lines will lie on the “grid” (integers).
::解答: 由于这两个方程式都是以斜坡界面形式呈现的, 我们可以绘制这些线条。问题在于两条线的交叉点是否在“ 电网 ” ( Intugers) 上。

The first equation has a y- intercept of 5 and of -1. It is shown here graphed in blue .
::第一个方程式的 Y 截面为 5 和 - 1 。此处以蓝色图表显示。

The second equation has a y- intercept of 2 and a slope of $\begin{align*}\frac{1}{2}\end{align*}$ . It is shown here graphed in red .
::第二个方程式的 Y 界面为 2 , 斜度为 12 , 此处以红色图表显示。

The two lines appear to intersect at (2, 3). Remember that we must always check the solution algebraically. Checking the solution :
::两条线似乎在(2,3)处交叉,要记住,我们必须始终检查溶液的代数。要检查溶液:

$\begin{aligned} (3) & = - (2) + 5 \\ 3 & = 3 \\ (3) & = \frac{1}{2} (2) + 2 \\ 3 & = 1 + 2 \\ 3 & = 3 \end{aligned}$
$\begin{align*}(3) &= -(2)+5\\ 3 &= 3\\ (3) &= \frac{1}{2}(2)+2 \\ 3 &= 1 + 2\\ 3 &= 3\\\end{align*}$

Having the graph drawn allows us to determine other values and trends in this situation. The blue line has a negative slope and as the weeks go on, the number of students attending that tutoring session decreases. The red line has a positive slope and as the weeks go on, the number of students attending that tutoring session increases. We can answer other questions like, "In what week does each tutoring session have 2 students?"
::绘制图后, 我们就可以确定其他的数值和趋势。蓝线有一个负斜度, 随着几周的继续, 参加辅导课程的学生人数会减少。红线有一个正斜度, 随着星期的继续, 参加辅导课程的学生人数会增加。我们可以回答其它问题, 比如 , “ 每期辅导课程在哪个星期有两名学生? ”

Substitution
::替代替代

Substitution is a good method to use when one of the variables is isolated in the equation or the coefficient of one of the variables is 1 or -1. When you isolate that variable to substitute into the other equation, you will not be introducing additional fractions into the problem. Let's consider an example of a good problem for substitution.
::当变量之一在方程中被孤立或变量之一的系数为 1 或 - 1 时,替代是一个很好的方法。当您将该变量孤立到另一个方程中以替代该变量时,您将不会在问题中引入额外的分数。让我们考虑一个好的替代问题的例子。

Example 2
::例2

Solve the system:
::解决系统:

$\begin{aligned} 15 x + y & = 24 \\ y & = - 4 x + 2 \end{aligned}$
$\begin{align*}15x+y &=24\\ y &= -4x+2\end{align*}$
::15x+y=24y4x+2

Solution: The $\begin{align*}y\end{align*}$ is isolated in the second equation, so this system is set up well for substitution. It is easiest here to use the second expression to substitute into the other equation and solve:
::解答: y 在第二个方程式中是孤立的, 所以这个系统设置得非常适合替换。这里最容易使用第二个表达式来替代另一个方程式和解答 :

$\begin{aligned} 15 x + (- 4 x + 2) & = 24 \\ 15 x - 4 x + 2 & = 24 \\ 11 x & = 22 \\ x & = 2 \end{aligned}$
$\begin{align*}15x+(-4x+2) &=24\\ 15x-4x+2 &=24\\ 11x &= 22\\ x &= 2\end{align*}$
::15x+(-4x+2)=2415x-4x+2=2411x=22x=2

Now solve for $\begin{align*}y\end{align*}$ :
::现在为 y 解决 :

$\begin{aligned} y & = - 4 (2) + 2 \\ y & = - 8 + 2 \\ y & = - 6 \end{aligned}$
$\begin{align*}y &= -4(2)+2\\ y &= -8+2\\ y &= -6\end{align*}$
::y4(2)+2y8+2y6

The solution is (2, -6).
::解决办法是2,6。

Checking this solution :
::正在检查此解决方案 :

$\begin{aligned} 15 (2) + (- 6) & = 30 - 6 = 24 \\ - 6 = - 4 (2) + 2 & = - 8 + 2 = - 6 \end{aligned}$
$\begin{align*}15(2)+(-6) &= 30-6=24\\ -6 =-4(2)+2 & =-8+2=-6 \end{align*}$

Example 3
::例3

A rental car company, Affordable Autos, charges $30 per day plus $0.51 per mile driven. A second car rental company, Cheap Cars, charges $25 per day plus $0.57 per mile driven. For a short distance, Cheap Cars offers the better deal. At what point (after how many miles in a single day) does the Affordable Autos rental company offer the better deal?
::第二家汽车租赁公司,廉价汽车,每天25美元,每英里0.57美元。短期而言,廉价汽车提供了更好的交易。廉价汽车租赁公司在什么时候(在一天里多英里之后 ) 提供了更好的交易?

Solution: Set up equations to represent the total cost (for one day’s rental) for each company:
::解决方案: 设置方程式, 以代表每家公司的总成本( 一天租金) :

Affordable Autos $\begin{align*}\Rightarrow y=0.51x+30\end{align*}$
::负担得起的自动 y=0.51x+30

Cheap cars $\begin{align*}\Rightarrow y=0.57x+25\end{align*}$
::廉价汽车 *y=0.57x+25

The y is isolated in both equations here . Substituting $\begin{align*}y=0.51x+30\end{align*}$ into the second equation, we get:
::y 在两个方程式中是孤立的。将 y= 0. 51x+30 替换为第二个方程式, 我们得到 :

$\begin{aligned} 0.51 x + 30 = 0.57 x + 25 \\ 5 = 0.06 x \\ x = 83. \bar{333} \end{aligned}$
$\begin{align*}0.51x+30 = 0.57x+25\\ 5 = 0.06x\\ x = 83.\overline{333}\end{align*}$
::0.51x+30=0.57x+255=0.06xx=83.333

Therefore, Affordable Autos has a better deal if we want to drive more than 83 and one-third miles during our one-day rental.
::因此,如果我们想在我们一天的租用期间驾驶83英里和三分之一英里以上,那么,负担得起的汽车公司就有更好的交易。

by CK-12 provides a comparison of the methods that can be used to solve a system of linear equations.
::CK-12 提供了可用于解决线性方程式系统的方法比较。

Elimination by Addition
::以加

If the coefficients of a variable are additive inverses, then elimination by addition is a good choice.
::如果变量的系数是复数反数,那么通过加法消除是一个很好的选择。

Example 4
::例4

Solve the following system:
::解决以下系统:

$\begin{aligned} 4 x + 5 y & = 4 \\ - 4 x & = - 2 y - 11 \end{aligned}$
$\begin{align*}4x + 5y &= 4\\ -4x &= -2y-11\end{align*}$
::4x+5y=4-4x_4x___________________________

Solution: On the left side of this equation, the two x - terms have additive inverse coefficients. Stacking the like terms so that we can add gives us
::解决方案:在这个方程的左侧,两个x-条件具有添加的反系数。堆放相似的术语, 这样我们就可以添加

$\begin{aligned} 4 x + 5 y = 4 \\ + \underline{- 4 x + 2 y = - 11} \\ 7 y = - 7 \\ y = - 1 \end{aligned}$
$\begin{align*}\ 4x + 5y = 4 \ \quad \\ + \underline{-4x +2y = -11} \\ \qquad 7y = -7 \ \ \\ \qquad y=-1 \ \ \\\end{align*}$ Substituting into the first equation, we can solve for x.
::4x+5y=4 4x+2y11_7y7y7y1 替代第一个方程式,我们可以解决 x。

$\begin{aligned} 4 x + 5 (- 1) & = 4 ⟶ 4 x = 9 ⟶ x = \frac{9}{4} \end{aligned}$
$\begin{align*}4x + 5(-1) &= 4 \longrightarrow 4x=9 \longrightarrow x=\frac{9}{4}\\ \end{align*}$

::4x+5( - 1)=44x=94x=9x=94

Checking our solution gives us
::检查我们的解决方案给了我们

$\begin{aligned} 4 \cdot \frac{9}{4} + 5 \cdot - 1 = 4 & ⟶ 4 = 4 \\ - 4 \cdot \frac{9}{4} = (- 2 \cdot - 1) - 11 & ⟶ - 9 = - 9 \end{aligned}$
$\begin{align*}4 \cdot \frac{9}{4} + 5 \cdot -1 = 4 &\longrightarrow 4=4 \\ -4 \cdot \frac{9}{4} = (-2 \cdot -1) -11 &\longrightarrow -9=-9\end{align*}$

by CK-12 provides applications of solving a system of linear equations.
::CK-12提供解决线性方程式系统的应用。

Elimination by Multiplication and Addition
::乘数和加法除法

When none of the coefficients are 1 or -1 and there are no additive inverses, then you can use elimination by multiplication and addition.
::当没有一个系数为 1 或 - 1, 并且没有添加反差时, 您可以通过乘法和加法来消除。

Example 5
::例5

Solve the system:
::解决系统:

$\begin{aligned} - 6 x + 11 y & = 86 \\ 9 x - 13 y & = - 115 \end{aligned}$
$\begin{align*}-6x+11y &= 86\\ 9x-13y &= -115\end{align*}$
::- 6x+11y=869x-13y=115

Solution: Since the LCM of 6 and 9 is 18, we will multiply the first equation by 3 and the second equation by 2 to eliminate $\begin{align*}x\end{align*}$ first:
::解答:既然6和9的LCM是18,我们将将第一个方程式乘以3,第二个方程式乘以2,以消除x1:

$\begin{aligned} 3 (- 6 x + 11 y = 86) \Rightarrow - 18 x + 33 y = 258 \\ 2 (9 x - 13 y = - 115) \underline{18 x - 26 y = - 230} \\ 7 y = 28 \\ y = 4 \end{aligned}$
$\begin{align*}& 3(-6x+11y=86) \quad \Rightarrow \quad - \cancel{18x}+33y=258\\ & \ \ 2(9x-13y=-115) \qquad \quad \ \underline{\cancel{18x}-26y=-230 \; \; \;}\\ & \qquad \qquad \qquad \qquad \qquad \qquad \qquad \quad \ 7y=28\\ & \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad y=4\end{align*}$
::3(6x+11y=86)18x+33y=258 2(9x-13y115) 18x-26y230_7y=28y=4

Now solve for $\begin{align*}x\end{align*}$ :
::现在解析 x:

$\begin{aligned} - 6 x + 11 (4) & = 86 \\ - 6 x + 44 & = 86 \\ - 6 x & = 42 \\ x & = - 7 \end{aligned}$
$\begin{align*}-6x+11(4)&=86\\ -6x+44 &=86\\ -6x &=42\\ x &= -7 \end{align*}$
::-6x+11(4)=86-6x+44=86-6x=42x=7

Solution: (-7, 4)
::解决办法-7,4)

Checking our solution
::正在检查我们的解决方案

$\begin{aligned} - 6 (- 7) + 11 (4) & = 42 + 44 = 86 \\ 9 (- 7) - 13 (4) & = - 63 - 52 = - 115 \end{aligned}$
$\begin{align*}-6(-7)+11(4) &= 42+44=86\\ 9(-7)-13(4) &= -63-52=-115 \end{align*}$

by Krista King Math demonstrates three ways to solve a system of linear equations.
::Krista King Math用三种方法来解决线性方程式系统。

Summary
::摘要

It is best to use graphing when you may want to have a picture of the situation to analyze other aspects of the problem.
::最好在您想了解情况以分析问题其他方面时使用图表。

It is best to use substitution if one of the variables is isolated or has a coefficient of 1 or -1.
::如果一个变量是孤立的或系数为1或-1,则最好使用替代。

It is best to use elimination by addition when the coefficients of one of the variables are additive inverses.
::如果其中一个变数的系数是复数反数,最好通过加法来消除这些变数。

It is best to use elimination by multiplication and addition in the remaining cases.
::最好在其余情况下通过乘法和加法来消除这些疾病。

Review
::回顾

Solve the following systems of equations.
::解决以下方程式系统。

.

$\begin{align*}\eqalign{5x-2y &= -1\\ 8x+4y &= 56}\end{align*}$

.

$\begin{align*}\eqalign{3x+y &= -16\\ -4x-y &= 21}\end{align*}$

.

$\begin{align*}\eqalign{&7x+2y = 4\\ &y = -4x+1}\end{align*}$

.

$\begin{align*}\eqalign{-8x+10y &= -1\\ 2x-6y &= 2}\end{align*}$

.

$\begin{align*}\eqalign{3x+y &= 18\\ -7x+3y &= -10}\end{align*}$

.

$\begin{align*}\eqalign{2x+15y &= -3\\ -3x-5y &= -6}\end{align*}$

.

$\begin{align*}\eqalign{15x-y &= 19\\ 13x+2y &= 48}\end{align*}$

.

$\begin{align*}\eqalign{&x = -9y-2\\ &-2x-15y = 6}\end{align*}$

.

$\begin{align*}3x+12y = -18\\ y = -\frac{1}{4}x-\frac{3}{2}\end{align*}$

.

$\begin{align*}\eqalign{&-2x-8y = -2\\ &x = \frac{1}{2}y+10}\end{align*}$

.

$\begin{align*}\eqalign{14x+y &= 3\\ -21x-3y &= -3}\end{align*}$

.

$\begin{align*}\eqalign{&y = \frac{4}{5}x+7\\ &8x-10y = 2}\end{align*}$

Explore More
::探索更多

1. The sum of two numbers is 35. The larger number is one less than three times the smaller number. What are the two numbers?
::1. 两个数字的总和是35, 最大的数字是比较小的数字少1比3倍。这两个数字是多少?

by Mathispower4u provides a variety of applications of solving linear systems .
::由Mathispower4u提供各种解决线性系统的应用。



2. A rental car company rents cars for $125 a day and vans for $250 a day. If the company rented 27 vehicles and the receipts totaled $5,250, how many cars and how many vans did the company rent that day?
::2. 租车公司每天租用汽车125美元,每天租用面包车250美元,如果公司租用27辆汽车,收据共计5 250美元,公司当天租用多少辆汽车和多少辆面包车?

by CK-12 demonstrates how to write and solve systems for application problems.
::CK-12 演示如何为应用问题书写和解决系统。



3. Rachel offers to go to the coffee shop to buy cappuccinos and lattes for her coworkers. She buys a total of nine drinks for $35.75. If cappuccinos cost $3.75 each and the lattes cost $4.25 each, how many of each drink did she buy?
::3. Rachel主动提出去咖啡店为同事购买卡布奇诺和拿铁,她共购买九杯饮料35.75美元,如果卡布奇诺每杯3.75美元,拿铁每杯4.25美元,她每杯买多少?

4. The flight from San Francisco to Washington, DC, takes 4 hours and 50 minutes. The return flight takes 5 hours and 50 minutes ¹ . If we assume the plane covers the same distance and travels at an average speed of 500 miles per hour, approximately how fast is the wind speed?
::4. 从旧金山飞往华盛顿特区的飞行需要4小时50分钟,返回飞行需要5小时50分钟,如果我们假设飞机的距离相同,平均时速为500英里,风速大约有多快?

5. Nora wants 2% milk for a recipe. Unfortunately, she only has whole (3.5% milk fat) milk and skim (0.5% milk fat) milk. What combination of whole milk and skim milk can Nora use to replace 1 pint of 2% milk in her recipe?
::5. Nora想要2%的牛奶作为食谱,但不幸的是,她只有全部(3.5%的奶脂)牛奶和脱脂(0.5%的奶脂)牛奶。 Nora能用什么结合牛奶和脱脂牛奶来取代食谱中的1品脱2%的牛奶?

6. Dave purchases 4 monthly passes and then takes 30 rides where he pays per ride. This costs $467.50. Hailey purchases 3 monthly passes and then pays per ride for 21 rides. This costs $347.25. How much is a monthly pass and how much does it cost to pay per ride? ²
::6. Dave每月购买4份通行证,然后乘30次旅程,每次旅程他付费,费用467.50美元,Hailey每月购买3份通行证,然后支付21次旅程的每次旅程费用347.25美元,每月通行证多少钱,每次旅程支付多少钱?

by CK-12 provides even more application of linear systems.
::CK-12提供的线性系统的应用甚至更多。

Answers for Review and Explore More Problems
::回顾和探讨更多问题的答复

Please see the Appendix.
::请参看附录。

References
::参考参考资料

1. "Flight Time from San Francisco, CA to Washington, DC, last accessed May 17, 2017, http://www.travelmath.com/flying-time/from/San+Francisco,+CA/to/Washington,+DC.
::1. “从旧金山、加利福尼亚到华盛顿特区的短暂时间,最后一次访问时间是2017年5月17日,http://www.travelmath.com/ flying-time/from/San+Francisco,+CA/to/Washington,+DC。

2. "CTA Fare Information," effective January 2013, http://www.transitchicago.com/fares/.
::http://www.trasitchicago.com/fares/。

Section outline

General

确定解决公平体系时采用的最佳方法

What Is the Best Method? ::什么是最佳方法?

Graphing ::图表绘制

Example 1 ::例1

Substitution ::替代替代

Example 2 ::例2

Example 3 ::例3

Elimination by Addition ::以加

Example 4 ::例4

Elimination by Multiplication and Addition ::乘数和加法除法

Example 5 ::例5

Summary ::摘要

Review ::回顾

Explore More ::探索更多

Answers for Review and Explore More Problems ::回顾和探讨更多问题的答复

References ::参考参考资料

What Is the Best Method?
::什么是最佳方法?

Graphing
::图表绘制

Example 1
::例1

Substitution
::替代替代

Example 2
::例2

Example 3
::例3

Elimination by Addition
::以加

Example 4
::例4

Elimination by Multiplication and Addition
::乘数和加法除法

Example 5
::例5

Summary
::摘要

Review
::回顾

Explore More
::探索更多

Answers for Review and Explore More Problems
::回顾和探讨更多问题的答复

References
::参考参考资料