5.4 寻找职能的领域和范围

Section outline

• Select section General

  Collapse Expand

  General

  Collapse all Expand all

  • Select activity 新闻通告

    

    新闻通告 Forum
• Select section 查找函数的域和范围

  Collapse Expand

  查找函数的域和范围

  播放段落

  The Bay of Fundy between New Brunswick and Nova Scotia, Canada, has the highest tides in the world. High tide can reach as high as 56 feet. (For comparison, the highest tides in the United States are in Alaska at 40 feet and the highest tides in the continental U.S. are in Maine, not far from the Bay of Fundy, at about 20 feet). ¹ Over a course of a day, we can model the tides in the Bay of Fundy with a function where time corresponds to the height of the water. What are the possible values that we can put in this function? What are the possible values that this function outputs? These questions can be answered by identifying the domain and range as we discuss in this section. 
  ::新不伦瑞克与加拿大新斯科舍之间的方济湾是世界最高潮位。高潮可以高达56英尺。 (相比之下,美国最高潮位在阿拉斯加,40英尺,美国大陆最高潮位在美国缅因州,离丰迪湾不远,大约20英尺)。 1 在一天之内,我们可以模拟方济湾的潮流,其函数与水的高度相匹配。我们可以在这个函数中设定什么值?这一函数输出的可能值是什么?这些问题可以通过我们在本节中讨论的域和范围来解答。

  

  播放段落

  Domain and Range
  ::域和范围

  播放段落

  The domain of a relation is the possible set of inputs. This is helpful because it tells someone using the relation what values they can input into the relation and expect to get an output.
  ::关系领域是可能的一组输入。 这很有帮助, 因为它告诉使用关系的人, 他们可以输入到关系中哪些值, 并期望得到输出 。

  播放段落

  The range of a relation is the possible set of outputs. It tells someone using the relation what values to expect as outputs. 
  ::关系的范围是可能的一组产出。 它告诉使用这种关系的人什么值可以期望为产出。

  播放段落

  Example 1
  ::例1

  播放段落

  Find the domain and range of the following relation:  {(9, 2), (7, -3), (4, -6), (-10, 4), (-2, -7)}. Determine if the relation is a function.  
  ::查找下列关系的域和范围 {(9, 2), (7, 3), (4, 6), (10, 4), (2, 7) 。 确定该关系是否是一个函数 。

  播放段落

  Solution: First, this is a function because each  x- value has only one y- value. The domain is the possible inputs or the x- values. The range is the possible outputs or the y- values. Notice the notation.
  ::解决方案 : 首先, 这是一个函数, 因为每个 x 值只有一个 Y 值。 域是可能的输入或 x 值。 范围是可能的输出或 y 值。 注意标记 。

  播放段落

  $$\begin{array}{rl}& x\in \{9,7,4,-10,-2\}\\ & y\in \{2,-3,-6,4,-7\}\end{array}$$

  
  ::x9,7,4,4-10,-2,2,3,6,4-7}

  播放段落

  The $\begin{array}{r}\in \end{array}$ symbol means “an element of.” The curly brackets , { }, around the  x-  and y- values, indicate that these numbers make a set. In words, you would say, “ $\begin{array}{r}x\end{array}$ is an element of the set 9, 7, 4, -10, and 2.”
  ::符号指“ 元素 ” 。 在 x 和 y 值周围的卷括号 {} 表示这些数值组成一组。 换句话说, 您会说 , “ x 是 9 、 7 、 4 、 10 和 2 集的一个元素 。 ”

  播放段落

  by CK-12 demonstrates how to identify domain and range. 
  ::CK-12 显示如何识别域和范围。

   

  播放段落

  Example 2
  ::例2

  播放段落

  Find the domain and range of $\begin{array}{r}y=x-3\end{array}$ .
  ::查找 y=x-3 的域域和范围。

  播放段落

  Solution:  To determine the domain, think about the operation being performed here. The formula says that you take a number and subtract 3. Is there any number you cannot subtract 3 from? 
  ::解决方案 : 要确定域名, 请想一想这里正在执行的操作 。 公式表示您要取一个数字然后减去 3 。 是否有任何数字您不能从中减去 3 ?

  播放段落

  You can subtract 3 from any number, so the domain is all real numbers. As we saw in Chapter 1, we have two ways to write this, either in interval notation or set-builder notation. So, the domain is
  ::您可以从任意数字中减去 3 , 所以域是所有真实数字。 正如我们在第一章中看到的那样, 我们用两种方法来写这个, 要么用间距符号, 要么用设置创建者符号来写。 因此, 域是

  播放段落

  $$\begin{array}{rlrl}& \text{dom}y=\{x\in \mathbb{R}\}& & \text{dom is an abbreviation for domain}\\ \\ & \text{OR}\\ \\ & \text{dom}y=(-\mathrm{\infty },\mathrm{\infty })\end{array}$$

  
  ::域 y= (,,) 的缩写

  播放段落

  To determine the range, it is helpful to see the graph of the function. As we can see on the graph below, the arrows indicate the graph will continue on forever in both directions and so will have a point on the graph that corresponds to every number on the axis or all real numbers.
  ::要确定范围, 查看函数的图形会很有帮助。 正如我们在下图中看到的, 箭头显示的图形将双向永久持续, 因此在图形上将有一个与轴上每个数字或所有实际数字相对应的点 。

  

  播放段落

  We can write this similar to the above. 
  ::我们可以写出类似上述内容的文字。

  播放段落

  $$\begin{array}{rlrl}& \text{ran}y=\{y\in \mathbb{R}\}& & \text{ran is an abbreviation for range}\\ \\ & \text{OR}\\ \\ & \text{ran}y=(-\mathrm{\infty },\mathrm{\infty })\end{array}$$

  
  ::rareORran y= (,) 的缩写

  播放段落

  by Mathispower4u  demonstrates how to identify the domain and range of the graph of a function . 
  ::by Mathispower4u 演示如何识别函数图形的域和范围。

   

  播放段落

  Example 3
  ::例3

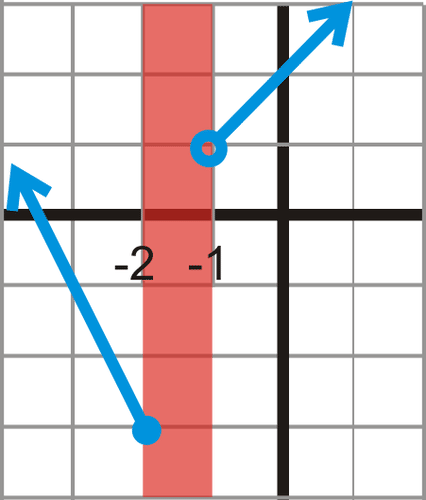
  播放段落

  Find the domain and range of the graphed function below.
  ::查找以下图形化函数的域和范围。

  

  播放段落

  Solution: This is a function, even though it might not look like it. This type of function is called a piecewise-defined function because it is defined as different pieces of functions on different intervals.
  ::解答 : 这是一个函数, 即使它看起来可能不像它。 这种类型的函数被称为小字节定义的函数, 因为它被定义为不同间隔的不同函数块 。

  播放段落

  To find the domain, look at the possible x- values. Notice that when $\begin{array}{r}x\end{array}$ is between -2 and -1 it is not defined, or there are no points. The closed circle at -2 indicates that the function is defined there, but the open circle at -1 indicates the function is not defined at -1. 
  ::要查找域, 请查看可能的 x 值 。 注意当 x 在 -2 和 -1 之间时, 没有定义它, 或者没有点 。 - 2 上的封闭圆表示函数是在那里定义的, 但是 - 1 上的开放圆表示函数不是在 - 1 上定义的 。

  

  播放段落

  We can write this in interval notation as  $\begin{array}{r}x\in (-\mathrm{\infty },-2]\cup (-1,\mathrm{\infty })\end{array}$  or in set-builder notation as $\begin{array}{r}\{x\in \mathbb{R}|x\le -2\text{or}x>-1\}\end{array}$ .
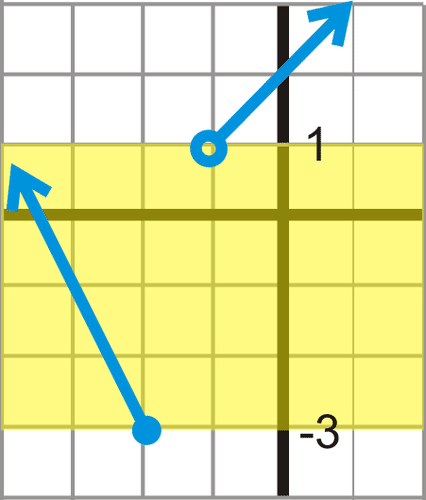
  ::我们可以以 {x}{{{{{{}}} {{}} {} {} 或 x} {} 的间隔编号写成 x{{{{},_2}}} {} 或设置-构建者标记为{{{{{} {{} x} {} {} 或 x} {} 。

  播放段落

  To find the range, we need to look at the possible y- values. Changing our viewpoint to look at the y- axis, at first glance, it looks like the function is not defined from -3 to 1.
  ::要找到范围, 我们需要查看可能的 Y 值 。 改变我们的观点以查看 Y 轴, 乍一看, 看起来函数没有定义从 - 3 到 1 。

  播放段落

  However, upon further investigation, the piece on the left does pass through the yellow region, below, where we thought the function was not defined. This means that the function is defined between -3 and 1. Below -3, there are no points on the graph. Thus, the range is $\begin{array}{r}y\in [-3,\mathrm{\infty })\end{array}$  or  $\begin{array}{r}\{y\in \mathbb{R}|y\ge -3\}\end{array}$ . 
  ::然而,经过进一步调查,左侧的碎片确实穿过黄区域,下面的黄区域, 我们认为函数没有定义。 这意味着函数定义在 - 3 和 1. 之间, 下面 - 3 上没有点。 因此, 范围是 y {_ 3 { { 3 } 或 {yR { { y 3 } 。

  

  播放段落

  Example 4
  ::例4

  播放段落

  Find the domain and range of  $\begin{array}{r}y=x^2\end{array}$ . 
  ::查找 y=x2 的域域和范围。

  播放段落

  Solution:  The domain is the possible set of inputs, so our question is: is there a number that you cannot square? You can square any number, so our domain is all real numbers, either  $\begin{array}{r}\text{dom}y=\{x\in \mathbb{R}\}\end{array}$  or  $\begin{array}{r}\text{dom}y=(-\mathrm{\infty },\mathrm{\infty })\end{array}$ .
  ::解决方案 : 域是可能的输入集, 所以我们的问题是 : 是否有一个数字不能平方 ? 您可以平方任何数字, 因此我们的域是所有真实数字, 要么是 dom y xR} , 要么是 dom y = (, ) 。

  播放段落

  Usually, it is helpful to draw a graph, but in this case, we might be able to reason without one. What happens to a number when you square it? It is either 0 or a positive number, so the range is 0 and the positive numbers, that is, $\begin{array}{r}\text{ran}y=\{y\in \mathbb{R}|y\ge 0\}\end{array}$  or $\begin{array}{r}\text{ran}y=(0,\mathrm{\infty })\end{array}$ .   
  ::通常, 绘制图表是有用的, 但在此情况下, 我们也许可以解释。 当您平方时, 数字会怎样 ? 它不是 0 , 就是正数 。 所以范围是 0 , 正数 , 就是 y y y R y 0 或 y = 0 。

  播放段落

  Example 5
  ::例5

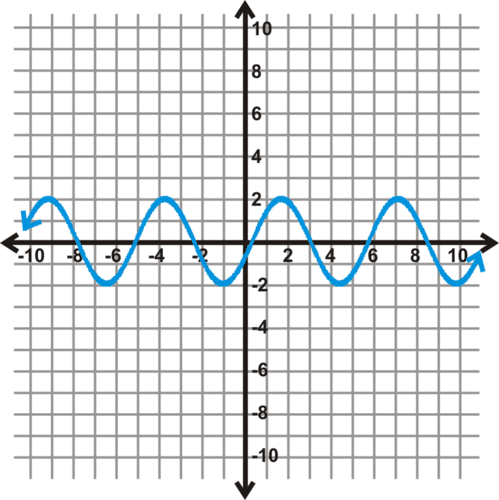
  播放段落

  Define the domain and range of the function that relates the time in minutes to the heights of the tides in the Bay of Fundy. 
  ::定义函数的域和范围,将时间以分钟计与丰迪湾潮汐的高度相联系。

  播放段落

  Solution:  The span between low and high tide is 6 hours and 13 minutes or 373 minutes. So, if we start our function at time 0 minutes, our domain is [0, 373]. 
  ::解决方案:低潮和高潮之间的间隔是6小时13分钟或373分钟。所以,如果我们在0分钟时开始运行,我们的域是[0,373]。

  播放段落

  The output given a time is the height of the water. As we learned in the introduction, the water can be at any height between 0 feet and 56 feet, so the range is [0, 56]. 
  ::给定一个时间的输出是水的高度。 正如我们在引言中了解到的, 水可以在0英尺到56英尺之间的任何高度, 所以范围是 [ 0. 56] 。

  播放段落

  by Port Saint James shows a time lapse of the tides. 
  ::圣詹姆斯港显示潮水已过一段时间。

   

  播放段落

  Domain Problems
  ::域问题

  播放段落

  There are two domain problems that we can recognize from a formula. Let's explore them in the following examples. 
  ::有两个领域问题我们可以从公式中识别出来。让我们在下面的例子中加以探讨。

  播放段落

  Example 6
  ::例6

  播放段落

  Find the domain of  $\begin{array}{r}y=\frac{x+1}{x-2}\end{array}$ .
  ::查找 y=x+1x-2 的域名。

  播放段落

  Solution:  
  ::解决方案 :

  播放段落

  Since this function has a variable in the denominator, we have to be careful that the denominator is not equal to 0. Otherwise, we would be dividing by 0 and that is an illegal operation. 
  ::由于此函数在分母中存在变量,我们必须小心分母不等于0。 否则,我们将除以0,这是非法行为。

  播放段落

  To determine the domain, we set the denominator equal to 0 and solve. 
  ::为了确定域, 我们设定分母等于 0 并解析 。

  播放段落

  $$\begin{array}{r}x-2=0\\ \underset{\_}{+2+2}\\ x=2\end{array}$$

  
  ::x-2=0+2+2_x=2

  播放段落

  If $\begin{array}{r}x=2\end{array}$ , the denominator will be equal to 0 and we do not want that, so we eliminate 2 from our domain. So, the domain is $\begin{array}{r}\{x\in \mathbb{R}|x\ne 2\}\end{array}$  or  $\begin{array}{r}(-\mathrm{\infty },2)\cup (2,\mathrm{\infty })\end{array}$ .
  ::如果 x= 2, 分母将等于 0, 而我们不希望, 所以我们从我们的域中删除 2。 所以, 域是 {xR { { { { { { { { { { { { } { { } { } 或 (, 2}

  播放段落

  Example 7
  ::例7

  播放段落

  Find the domain of $\begin{array}{r}y=\sqrt{x+1}\end{array}$ .
  ::查找 y=x+1 的域名。

  播放段落

  Solution:
  ::解决方案 :

  播放段落

  Here, the problem is we cannot take a square root of a negative number and get a real number as a result. So, we need to make sure the expression underneath the radical , the radicand , is greater than or equal to 0. We set up an inequality and solve.
  ::问题在于我们无法从负数的平方根获取真实数字。 因此,我们需要确保激进线(radicand)下的表达方式大于或等于0。 我们设置了不平等并解决了不平等。

  播放段落

  $$\begin{array}{r}x+1\ge 0\\ \underset{\_}{-1-1}\\ x\ge -1\end{array}$$

  
  ::x+10 - 1 - 1_ x% 1

  播放段落

  This inequality tells us the values of x that will make the radicand positive or 0. Our domain is $\begin{array}{r}\{x\in \mathbb{R}|x\ge -1\}\end{array}$  or  $\begin{array}{r}[-1,\mathrm{\infty })\end{array}$ . Notice that there are some negative numbers in the domain. That is acceptable since we add 1 to them before taking the square root of the non-negative result.
  ::这种不平等告诉我们 x 的值是正值或正值。 我们的域是 {xR x1} 或 [ -1,\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\ x x x\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\

  播放段落

  by CK-12 demonstrates how to find the domain of a function given an equation .
  ::CK-12 显示如何找到函数的域, 给定方程式 。

   

  播放段落

  Feature: Catching Your Breath   
  ::特点:抓住你的呼吸

  播放段落

  by Jen Kershaw
  ::由Jen Kershaw著

  播放段落

  Have you ever wondered why it seems harder to catch your breath at the top of a mountain? There is in fact a connection between altitude and your ability to breath, and it can be described as a function.
  ::你有没有想过为什么在山顶呼吸起来似乎比较困难?事实上,高度与你的呼吸能力之间有联系,这可以说是一个函数。

  播放段落

  To understand why it is harder to breathe at higher elevations, you have to consider air pressure. At sea level, 21% of the air you breathe is oxygen. As you climb to higher altitudes, the percentage of oxygen remains the same, but air pressure decreases. Lower pressures mean air particles can spread out further, becoming more dispersed. In other words, the density of air also decreases with altitude. Since there are less oxygen molecules per unit volume of air, it becomes more difficult to breathe.
  ::要理解为什么在高海拔地区呼吸较难,你必须考虑气压。在海平面,你呼吸的空气中有21%是氧气。随着你升到高空,氧气的比例保持不变,但空气压力却在下降。低压力意味着空气颗粒会进一步扩散,更加分散。换句话说,空气密度也会随着高度的升高而下降。由于每单位空气量的氧分子较少,呼吸就变得更加困难。

  

  播放段落

  The higher up you climb, the harder your body has to work to absorb the oxygen. At extreme heights, altitude sickness can set in. Symptoms include headaches, fatigue, dizziness, or nausea. Altitude sickness commonly occurs at elevations greater than 8,000 feet, though symptoms can begin to appear around 6,500 feet above sea level.
  ::爬得越高, 你的身体就越难工作吸收氧气。 在极高的高度, 高空疾病可以出现。 症状包括头痛、疲劳、眩晕或恶心。 高空疾病通常发生在超过8000英尺的高度, 尽管症状可能开始出现在海拔6,500英尺左右。

  播放段落

  How do functions relate to all of this? Well, functions describe the relationships between two variables—in which one impacts the other. Since altitude clearly has an impact on breathing ability, you could say that your ability to breathe is a function of your elevation above sea level.
  ::函数与所有这一切有何关联? 那么, 函数描述两个变量之间的关系, 其中一个影响另一个。 由于高度显然对呼吸能力有影响, 您可以说, 您的呼吸能力是海平面升高的函数 。

  播放段落

  by Shredded Sports Science explains the benefits of altitude training.
  ::Shredded Sport Science解释海拔训练的好处。

   

  播放段落

  Summary
  ::摘要

  播放段落
  • The domain is the set of possible inputs; the range is the set of possible outputs.
    ::域是一套可能的输入;范围是一套可能的输出。
  播放段落
  • On a graph, you can draw vertical and horizontal lines to help you determine the domain and range, respectively.
    ::在图形中,您可以绘制垂直线和水平线,帮助您分别确定域和范围。
  播放段落
  • To find the domain of a function that is a fraction, set the denominator equal to 0 to find values to rule out of the domain.
    ::要找到函数分数的域, 设置分母等于 0 的分母, 以找到要排除域的值 。
  播放段落
  • To find the domain of a function with a square root, set the radicand greater than or equal to 0 to find the values that should be in the domain. 
    ::要找到带平方根的函数域, 请设定值大于或等于 0 的弧度, 以找到域内的值 。

  播放段落

  Review
  ::回顾

  播放段落

  Find the domain and range of the following functions. 
  ::查找下列函数的域和范围。

  1.  {(8, 3), (-4, 2), (-6, 1), (5, 7)}

  2.  (5, 7), (3, 7), (2, 8), (8, 1)}

  3. 

  

  4. 

  

  5. 

  

  6. 

  

  7. 

   

  播放段落

  Find the domain of the following functions.
  ::查找下列函数的域。

  播放段落

  8.  $\begin{array}{r}y=|x|\end{array}$
  ::8 y y x

  播放段落

  9.  $\begin{array}{r}y=\frac{3}{x+4}\end{array}$
  ::9.y=3x+4 y=3x+4

  播放段落

  10.  $\begin{array}{r}y=\frac{4x}{x-5}\end{array}$
  ::10.y=4xx-5

  播放段落

  11.  $\begin{array}{r}y=\sqrt{x-7}\end{array}$
  ::11.y=x-7 y=7

  播放段落

  12.  $\begin{array}{r}y=\sqrt{1-x}\end{array}$
  ::12 y= 1 - x

  播放段落

  Explore More
  ::探索更多

  播放段落

  1.  Tina’s car travels about 30 miles on one gallon of gas. She has between 10 and 12 gallons of gas in the tank. Find the domain and range of the function to calculate how far she can drive.
  ::1. 蒂娜的汽车在一加仑的气体上行驶约30英里,坦克内有10至12加仑的气体,找到功能的域域和范围以计算她能开多远。

  播放段落

  2.  Bob had a summer job that paid $10.00 per hour and he worked between 20-25 hours every week. Write an equation that models his weekly salary where S is his weekly salary and h is the number of hours he worked per week. What is the independent variable for this problem? Describe the domain and range for this problem.
  ::2. Bob的夏季工作是每小时100美元,每周工作20至25小时。写一个公式,以他每周的工资为S的每周工资和h的每周工作小时数为模型。这个问题的独立变量是什么?描述这个问题的域和范围。

  播放段落

  3.  You just got a new part-time job at the mall that pays a base rate of $150/week plus $5/sale. Your boss encourages you to make as many sales as possible but she will cap your weekly earnings at $250. What are the domain and range of the function represented by this situation?
  ::3. 你刚在商场找到一份新的兼职工作,支付150美元/周的基本费率加上5美元/销售,你的老板鼓励你尽可能多地销售,但她会将每周收入限制在250美元。

  播放段落

  4.  Joseph drove from his summer home to his place of work. To avoid the road construction, Joseph decided to travel the gravel road. After driving for 20 minutes he was 62 miles away from work and after driving for 40 minutes he was 52 miles away from work. Represent the problem on a graph and write a suitable domain and range for the situation.
  ::4. Joseph从夏季回家到工作地点,为避免道路施工,Joseph决定走碎石路,在开车20分钟后,他离开工作62英里,在开车40分钟后,他离工作52英里,用图表表示问题,并写出适合这种情况的域域和范围。

  播放段落

  5.  Joanna and Macy are helping with a research project about how fish waste is affecting the local environment. They know that fish length is related to the amount of waste produced by each fish. They also know that fish in the fish farm can be anywhere from 2 inches to 30 inches. The amount of waste (in millimeters) per day is approximately equal to 0.62 times the fish length. What are the domain and range of he function that relates fish length to the amount of waste produced?
  ::5. Joanna和Mace正在帮助一项有关鱼废物如何影响当地环境的研究项目,他们知道鱼的长度与每条鱼产生的废物数量有关,他们还知道养鱼场内的鱼在2至30英寸之间,每天的废物(毫米)大约相当于鱼长度的0.62倍,他的职能的域和范围与产生的废物数量有关?

  播放段落

  Answers for Review and Explore More Problems
  ::回顾和探讨更多问题的答复

  播放段落

  Please see the Appendix. 
  ::请参看附录。

  播放段落

  PLIX
  ::PLIX

  播放段落

  Try these interactives that reinforce the concepts explored in this section:
  ::尝试这些强化本节所探讨概念的交互作用 :

  播放段落

  References
  ::参考参考资料

  播放段落

  1. "Where Is the Highest Tide?" last revised November 24, 2014, http://oceanservice.noaa.gov/facts/highesttide.html.
  ::http://oceanservice.noaa.gov/facts/highesttide.html.