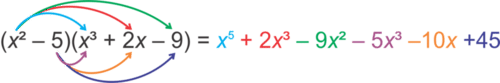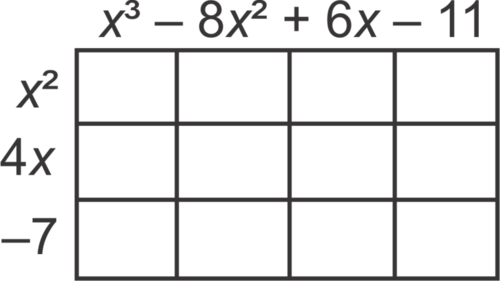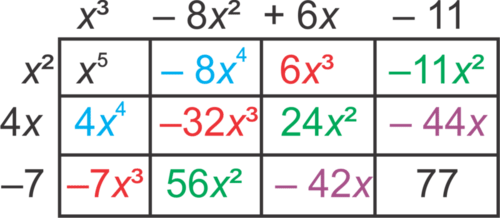6.5多项式乘法

Section outline

• Select section General

  Collapse Expand

  General

  Collapse all Expand all

  • Select activity 新闻通告

    

    新闻通告 Forum
• Select section 多项式乘法

  Collapse Expand

  多项式乘法

  Carolyn is making a quilt block for a quilt made by a group. The sizes of the quilt blocks will vary but all follow the same  pattern . We can express the area of a quilt block as a  polynomial function . In this section, we continue to see how to multiply  .

  

  [Figure 1]

  播放段落

  There are several different ways to organize your work when multiplying polynomials. We consider three ways here.
  ::乘以多面体时,您的工作有几种不同的组织方式。 我们在这里考虑三种方式。

  播放段落

  Multiplying Polynomials Horizontally
  ::水平水平乘以多多边

  播放段落

  Just as we do when we FOIL two binomials, when we multiply two polynomials, we want to distribute each of the  terms  in the first  polynomial  to the second polynomial. Let's consider an example. 
  ::就像我们当世界杯的两个二元论, 当我们乘以两个多元论时一样, 我们想把第一个多元论中的每一个术语 分配给第二个多元论。让我们举个例子。

  播放段落

  Example 1
  ::例1

  播放段落

  Find the product of  $\begin{array}{r}(x^2-5)(x^3+2x-9)\end{array}$ .
  ::查找 (x 2 - 5) (x 3+ 2 x - 9) 的产物 。

  播放段落

  Solution:  Take the  $\begin{array}{r}{x}^2\end{array}$  in the first polynomial and multiply it by every  term  in the second polynomial.
  ::解答: 在第一个多元体中取 x 2 乘以第二个多元体中的每个词。

  

  [Figure 2]

  播放段落

  Now, add to these terms the product of -5 and every term in the second polynomial.
  ::现在,在这些术语中加上 -5的产物 和第二个多语言的每一个产物。

  

  [Figure 3]

  播放段落

  Lastly, combine any  like terms . In this example, only the  $\begin{array}{r}{x}^3\end{array}$  terms can be combined.
  ::最后,将任何类似术语结合起来,在这个例子中,只有x 3术语可以合并。

  

  [Figure 4]

  播放段落

   by CK-12 demonstrates how to multiply polynomials  horizontally . 
  ::由 CK-12 演示如何水平乘以多数值 。

  播放段落

  Multiplying Polynomials Vertically
  ::垂直乘以多多边数

  播放段落

  Another way we can multiply polynomials is by organizing our work  vertically  just as we do with numbers.
  ::另一种我们可以乘以多面性的方法 是通过垂直组织我们的工作 就像我们用数字一样

  播放段落

  Example 2
  ::例2

  播放段落

  Find the product of  $\begin{array}{r}(x^2+3)(x^3+4x+2)\end{array}$ .
  ::查找 (x 2 + 3) (x 3 + 4 x + 2) 的产物 。

  播放段落

  Solution:  We will set up the  multiplication  just as we do with numbers where one number is above the other number.
  ::解答:我们将设置乘法, 就像我们用数字来设置乘法一样, 当一个数字高于另一个数字时。

  $$\begin{array}{r}{x}^3+4x+2\\ \underset{\_}{\times x^2+3}\end{array}$$

  播放段落

  Then, we multiply all of the terms in the top polynomial by 3. 
  ::然后,我们把顶层多面体中的所有条件乘以3。

  $$\begin{array}{r}{x}^3+4x+2\\ \underset{\_}{\times x^2+3}\\ 3x^3+12x+6\end{array}$$

  播放段落

  Next, we multiply all of the terms in the top polynomial by  $\begin{array}{r}{x}^2\end{array}$  and line up the like terms.
  ::接下来,我们乘以顶部多球体中所有词的乘以 x 2 并排成类似词组。

  $$\begin{array}{r}{x}^3+4x+2\\ \underset{\_}{\times x^2+3}\\ 3x^3+12x+6\\ \underset{\_}{+x^5+4x^3+2x^2}\end{array}$$

  Last, we add like terms.

  $$\begin{array}{r}{x}^3+4x+2\\ \underset{\_}{\times x^2+3}\\ 3x^3+12x+6\\ \underset{\_}{+x^5+4x^3+2x^2}\\ x^5+7x^3+2x^2+12x+6\end{array}$$

  播放段落

   by CK-12 demonstrates how to multiply two polynomials vertically.
  ::由 CK-12 演示如何垂直乘以两个多数值。

  播放段落

    WARNING
  ::警告

  播放段落

  A common mistake is to forget to multiply two terms together. For example,  $\begin{array}{r}(x-8)(x+3)\ne x^2+3x-24\end{array}$ .
  ::一个常见的错误是忘记将两个术语相乘。 例如, (x- 8) (x + 3) x 2 + 3 x - 24 ) 。

  播放段落

  A quick way to make sure you have the right number of terms before you combine like terms is to multiply the number of terms in the first polynomial by the number of terms in the second polynomial. In this example, we are multiplying two binomials, so  $\begin{array}{r}2\cdot 2=4\end{array}$ . We should have 4 terms before we combine like terms. 
  ::快速地确保您在组合类似术语之前拥有正确的术语数, 即将第一个多语种术语数乘以第二个多语种术语数。 在此示例中, 我们正乘以两个二进制词数, 所以 2 2 = 4 。 在合并类似术语数之前, 我们应该有四个术语数 。

  播放段落

  Multiplying Polynomials Using Charts
  ::使用图表乘法多多边

  播放段落

  An additional way to make sure you are distributing each term in one polynomial to the other polynomial is by setting up a chart. We consider this process in the following example. 
  ::另一种确保您将每个词以一个多义形式分配给另一个多义形式的方式是设置一个图表。我们在下面的例子中考虑这一过程。

  播放段落

  Example 3
  ::例3

  播放段落

  Multiply  $\begin{array}{r}(x^2+4x-7)(x^3-8x^2+6x-11)\end{array}$ .
  ::乘数(x2+4x-7)(x3-8x2+6x-11)

  播放段落

  Solution:  In this example, we will use the chart method. Align the two polynomials along the top and left side of a rectangle and make a row or column for each term. We will write the polynomial with more terms along the top of the box in this example.
  ::解答 : 在此示例中, 我们将使用图表方法 。 将矩形上方和左侧的两个多边形对齐, 并为每个术语绘制一行或一列 。 我们将在此示例中, 在框的顶端写一个多式词 。

  

  [Figure 5]

  播放段落

  Multiply each pair of terms together and fill in the corresponding blank in the box.
  ::将每一对术语一起乘以,填入盒子中相应的空白。

  

  [Figure 6]

  播放段落

  Finally, combine like terms. The final product is  $\begin{array}{r}{x}^5-4x^4-33x^3+69x^2-86x+77\end{array}$ .
  ::最终产品为 x 5 - 4 x 4 - 33 x 3 + 69 x 2 - 86 x 77。

  播放段落

   by MissKassner demonstrates how to use the chart method to multiply polynomials.  
  ::MissKassner 演示如何使用图表方法来乘以多数值。

  播放段落

  Example 4
  ::例4

  播放段落

  Find the area of a quilt block with the following piece lengths.
  ::找到一个有以下片段长度的裁缝块的区域 。

  

  播放段落

  Solution:  The side lengths are  $\begin{array}{r}3x^2+4x+1\end{array}$  and  $\begin{array}{r}{x}^2+4x+5\end{array}$ . To find the area, we multiply them.
  ::解析度:侧长为 3 x 2 + 4 x + 1 和 x 2 + 4 x + 5。要找到区域,我们乘以它们。

  $$\begin{array}{r}3x^2+4x+1\\ \underset{\_}{\times x^2+4x+5}\\ 15x^2+20x+5\\ 12x^3+16x^2+4x\\ \underset{\_}{+3x^4+4x^3+x^2}\\ 3x^4+16x^3+32x^2+24x+5\end{array}$$

     

  播放段落

  These are three methods to multiply polynomials. Use whichever method you are more comfortable with. Keep in mind, no matter which method you use, you will multiply every term in the first polynomial by every term in the second. Now, let's consider an example where there are more than two polynomials. 
  ::这些是乘数多义的三种方法。 使用您比较舒适的方法。 记住, 无论您使用哪种方法, 您都会在第一个多义中将每个词乘以第二个词中的每个词。 现在, 让我们来举一个例子, 有两个以上的多义 。

  播放段落

  Example 5
  ::例5

  播放段落

  Find the product of  $\begin{array}{r}(x-5)(2x+3)(x^2+4)\end{array}$ .
  ::查找 (x- 5) (2 x + 3) (x 2 + 4) 的产物 。

  播放段落

  Solution:  In this example, we have three binomials. When multiplying more than two polynomials, start by multiplying the first two polynomials together.
  ::解决方案 : 在此示例中, 我们有三个二元论。 当乘以两个多多边论时, 首先将前两个多多边论相乘 。

  $$\begin{array}{rl}(x-5)(2x+3)& =2x^2+3x-10x-15\\ & =2x^2-7x-15\end{array}$$

  播放段落

  Now, multiply the answer by the last  binomial .
  ::现在,将答案乘以最后一个二元论。

  $$\begin{array}{rl}(2x^2-7x-15)(x^2+4)& =2x^4+8x^2-7x^3-28x-15x^2-60\\ & =2x^4-7x^3-7x^2-28x-60\end{array}$$

  播放段落

   by CK-12 demonstrates how to multiply three polynomials.  
  ::由 CK-12 演示如何乘以 3 个多元数 。

  播放段落

  Summary
  ::摘要

  播放段落
  • There are three ways to organize multiplying polynomials by polynomials: horizontally, vertically, or the chart method. 
    ::有三种方法通过多面体组织乘数多面体:水平、垂直或图表方法。
  播放段落
  • To multiply polynomials, distribute each term in the first polynomial to the second polynomial, then combine like terms.
    ::乘以多义, 在第一个多义中将每个词分布到第二个多义中, 然后将类似术语合并起来 。

  播放段落

  Review
  ::回顾

  播放段落

  Find the product.
  ::找到产品。

  播放段落

  1.  $\begin{array}{r}(x^2+1)(x^2-2x-1)\end{array}$
  ::1. (x 2+1) (x 2 - 2 - 2 x - 1)

  播放段落

  2.  $\begin{array}{r}(5x-1)(x^3+8x-12)\end{array}$
  ::2. (5x--1) (x3+8x-12)

  播放段落

  3.  $\begin{array}{r}(x^2-6x-7)(3x^2-7x+15)\end{array}$
  ::3. (x 2 - 6 x - 7) (3 x 2 - 7 x 7 + 15)

  播放段落

  4.  $\begin{array}{r}(4x^3-x^2-3)(2x^2-x+6)\end{array}$
  ::4. (4 x 3 - 3 x 2 - 3) (2 x 2 - x + 6)

  播放段落

  5.  $\begin{array}{r}(x-1)(2x-5)(x+8)\end{array}$
  ::5. (x - 1) (2 x - 5) (x x + 8)

  播放段落

  6.  $\begin{array}{r}(2x^2+5)(x^2-2)(x+4)\end{array}$
  ::6. (2 x 2 + 5) (2 x 2 - 2) (x + 4)

  播放段落

  7.  $\begin{array}{r}(x^2-1)(3x-4)(3x+4)\end{array}$
  ::7. (x 2 - 1) (3 x - 4) (3 x + 4)

  播放段落

  8.  $\begin{array}{r}(2x^3-6x^2+x+7)(5x^2+2x-4)\end{array}$
  ::8. (2 x 3 - 6 x 2 + x + 7 ) (5 x 2 + 2 + 2 x 4 )

  播放段落

  9.  $\begin{array}{r}(x^3+x^2-4x+15)(x^2-5x-6)\end{array}$
  ::9. (x 3 + 3 + x 2 - 4 x + 15) (x 2 - 5 x - 6)

  播放段落

  10.  $\begin{array}{r}(4x^2-6x+11)(-3x^3+x^2+8x-10)\end{array}$
  ::10. (4 x 2 - 6 x + 11) (- 3 x 3 + 2 x 2 + 8 x + 10)

  播放段落

  Explore More
  ::探索更多

  播放段落

  1. If the polynomial  $\begin{array}{r}x-c\end{array}$  is a factor of the polynomial function  $\begin{array}{r}f(x)\end{array}$ , then  $\begin{array}{r}(c,0)\end{array}$ is an  x -intercept. Find a polynomial with  x -intercepts at  $\begin{array}{r}x=-4,1,3\end{array}$ .
  ::1. 如果多数值x-c是多数值函数f(x)的一个系数,那么(c,0)是一个 X 界面。在 x = = - 4, 1, 3 时找到带有 x 界面的多数值倍数。

  播放段落

  2. Find a polynomial with  x -intercepts at -2 and 6 and another factor of  $\begin{array}{r}(x^2+4)\end{array}$ .
  ::2. 在-2和6处和另一个因数(x 2+ 4)中找到带有 x 拦截器的多元值。

  播放段落

  3. What is a possible polynomial for this graph?
  ::3. 本图可能采用什么多面性图?