章节大纲

  • 常规

    全部折叠 展开全部

  • 一对一功能

    You take a survey of your friends' feelings about clowns.  Jack, Michelle, and Fatima like clowns. Miguel and Cindy do not. We can express this information as a table of values by mapping the friends to their opinions about clowns. This would be a function.
    ::米格尔和辛迪没有。我们可以通过绘制朋友对小丑的看法来表达这个信息作为价值表。这将是个函数。

    What if we wanted to switch the function from mapping the opinions about clowns to the friends? Would this still be a function? For the switched function to be a function, the original function has to satisfy a property called one-to-one . We cover how to identify functions with this property in this section. 
    ::如果我们想要将函数从绘制小丑观点转换为朋友, 那么该函数会如何? 这是否仍是一个函数? 如果调换的函数要成为函数, 原始函数必须满足一个名为一对一的属性。 我们在本节中覆盖如何识别此属性的函数 。

    lesson content

    One-to-One Functions
    ::一对一功能

    In this chapter, we will study two types of functions that are inverses of one another. To be , they need to satisfy a property of functions called one-to-one. 
    ::在本章中,我们将研究两种相互对立的功能:它们需要满足被称为一对一的功能特性。

      One-to-one Functions
    ::一对一函数

    A one-to-one function is a function where each output corresponds to a unique input. Formally, if f ( x 1 ) = f ( x 2 ) , then x 1 = x 2 .   

    This definition may sound familiar. It is similar to the definition of a function: a relation in which each input corresponds to a unique output. 
    ::这一定义可能听起来很熟悉。 它与函数的定义相似:每种输入与独特输出对应的关系。

    We can also consider this definition from another perspective. If  x 1 ≠ x 2 , then f ( x 1 ) ≠ f ( x 2 ) , or different inputs will have different outputs. Let's see how this works in some examples.   
    ::我们也可以从另一个角度来考虑这个定义。 如果 x1\\\\\x2, 那么f( x1)\\\\\\\\f(x2) 或不同的投入将会有不同的输出。 让我们来看看这些例子是如何运作的 。

    Example 1
    ::例1

    Determine whether the following function is one-to-one: { ( 1 , 2 ) , ( 3 , 4 ) , ( 2 , 5 ) , ( 4 , 1 ) } .
    ::确定以下函数是否一对一:{(1),2,(3,4),(2,5),(4,1)}。

    Solution: To determine if this function is one-to-one, we focus on the y -values. The  y -value 2 corresponds only  to 1; the y -value 4 corresponds only to 3; and, the y -values of 5 and 1 correspond to different numbers as well. This function satisfies the one-to-one property.  
    ::解决方案: 要确定此函数是否为一对一, 我们的焦点是 Y 值。 Y 值 2 仅对应于 1; Y 值 4 仅对应于 3; y 值 5 和 1 的 Y 值也对应不同数字。 此函数满足一对一的属性 。

    Example 2
    ::例2

    Determine whether the following function is one-to-one: 
    ::确定以下函数是否一对一:

    Friend Feeling About Clowns
    Jack Like
    Miguel Dislike
    Michelle Like
    Cindy Dislike
    Fatima Like

    Solution: If this function were one-to-one, then "Like" would correspond to only  one friend. The output "Like" corresponds to three different inputs, the  friends Jack, Michelle, and Fatima. Similarly, the output "Dislike" corresponds to two different friends, Miguel and Cindy. This function is not one-to-one. 
    ::解决方案 : 如果此函数是一对一, 那么“ 像” 只会对应一个朋友 。 输出“ 像” 对应三个不同的输入, 即朋友 Jack、 Michelle 和 Fatima 。 同样, 输出“ 不相似” 对应两个不同的朋友 Miguel 和 Cindy 。 此函数不是一对一 。

    Example 3
    ::例3

    Determine whether the following functions are one-to-one:  
    ::确定下列功能是否一对一:

    a. 
    ::a 。

    b. 
    ::b. b. 数据

    Solution:
    ::解决方案 :

    a. This function is not one-to-one because the output x corresponds to  b and  c . Another way to look at this is that  b and  c both map to the same output,  x.   
    ::a. 此函数不是一对一,因为输出x与b和c相对应。 另一种观点是,b和c两者的映射都与相同的输出x相同。

    b. This function is one-to-one. Each of the outputs,  x ,  y , and  z , corresponds to unique inputs,  a ,  b , and  c.  Another way to see this is that the inputs all map to different outputs. 
    ::b. 此函数为一对一。每项产出,即x、y和z,对应独特的投入,a、b和c。 另一种方式是将所有输入图都输入到不同的产出中。

     by utexascnsquest defines one-to-one functions and provides examples of identifying one-to-one functions. 
    ::通过 utxascnsquest 定义一对一的函数,并提供一对一函数的识别示例。

     

    Horizontal Line Test
    ::水平线测试

    As we saw above, the definition of a one-to-one function is similar to the definition of a function itself. We had a way to identify whether the graph of a relation was the graph of a function by using the vertical line test. Here we can use a similar test to determine if a function is a one-to-one function. 
    ::正如我们在上面所看到的,一对一函数的定义与函数本身的定义相似。我们有办法通过使用垂直线测试来确定关系图是否为函数图。在这里,我们可以使用类似的测试来确定函数是否为一对一函数。

      Horizontal Line Test
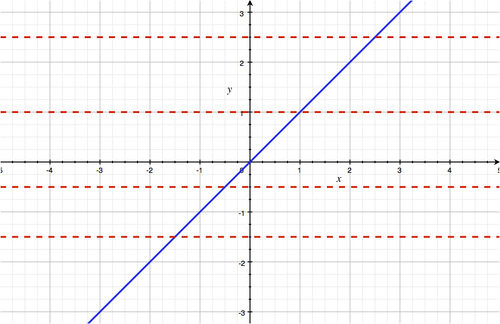
    ::水平线测试

     A function is a one-to-one function if and only if every horizontal line drawn through the graph intersects it at most once. 

    Example 4
    ::例4

    Determine whether the following function is one-to-one: 
    ::确定以下函数是否一对一:

    Solution: This graph is a graph of a one-to-one function. If you draw horizontal lines across the graph, those lines will only intersect the graph once.  
    lesson content


    ::解析度 : 此图是一对一函数的图形。 如果您在图形上绘制水平线, 这些线只将图形交叉一次 。

    Example 5
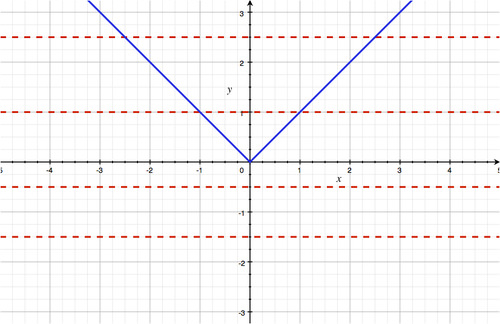
    ::例5

    Determine whether the following function is one-to-one:
    ::确定以下函数是否一对一:

    Solution: This graph is not the graph of a one-to-one function. If you draw horizontal lines above the x -axis, those lines will intersect the graph twice.  
    ::解析度 : 此图不是一对一函数的图形。 如果您在 X 轴上方绘制水平线, 这些线将两次交叉图形 。

    lesson content

    by The Inside Scoop on Algebra distinguishes between the horizontal and vertical line tests.
    ::以《代数上的内窥镜》区分水平和垂直线测试。

     

       How to Determine if Functions Are One-to-One Using Desmos
    ::如何确定函数是否一对一使用代数

    Be careful when trying to determine if functions are one-to-one when using a graphing utility. Graphing calculators often make parts of the graph look horizontal when they are not. Z oom in to see if the graph is actually horizontal. 
    ::当试图确定函数在使用图形工具时是否为一对一时要小心。 图形计算器通常使图形的部分在不时水平显示。 放大以查看图形是否实际上是水平显示 。

     

       How to Determine if Functions Are One-to-One Using a TI-83/84
    ::如何使用TI-83/84确定函数是否一对一

    Be careful when trying to determine if functions are one-to-one when using a graphing utility. Graphing calculators often make parts of the graph look horizontal when they are not. Zoom in to see if the graph is actually horizontal.   
    ::当试图确定函数在使用图形工具时是否为一对一时要小心。 图形计算器通常使图形的部分在不时水平显示。 放大以查看图形是否实际上是水平显示 。

    Summary 
    ::摘要

    • A function is one-to-one if  f ( x 1 ) = f ( x 2 )  implies  x 1 = x 2 . 
      ::如果 f( x1) =f( x2) 意味着 x1=x2, 一个函数为一对一。
    • We can see that a function is one-to-one by using the horizontal line test: If every horizontal line drawn through the graph intersects it at most once, then the function is one-to-one.
      ::通过水平线测试,我们可以看到一个函数是一对一:如果通过图形绘制的每一水平线最多一次交叉,则函数是一对一。

    Review
    ::回顾

    Which functions are one-to-one?
    ::哪些功能是一对一?

    1. {(3,28),(4,29),(4,30),(6,31)}

    2. {(4,5),(9,6),(7,8),(23,5)}

    3. {(8,18),(33,4),(5,16),(7,19)}

    For the following to be a one-to-one function, X cannot be what values?
    ::要将以下函数变成一对一函数, X 不能是什么值 ?

    4. {(9,12),(35,6),(7,18),(12,X)}
    ::4.{(9,12),(35,6),(7,18),(12,X)}

    5. {(20,21)(21,14),(110,112),(X,7)}
    ::5.{(20,21,21,14),(110,112),(X,7)}

    Are the following functions? If so, is the function one-to-one?
    ::下列函数是一对一的函数吗?如果是,函数是一对一吗?

    5.  f ( x ) = x 2  
    ::5.f(x)=x2

    6.  f ( x ) = x 3  
    ::6. f(x)=x3

    7.  f ( x ) = 1 x  
    ::7. f(x)=1x

    8.  f ( x ) = x n ,   n > 0  
    ::8. f(x)=xn, n>0

    9.  x = y 2 + 2  
    ::9. x=y2+2

    10.

    11. 

    12. 

    13. 

    14. 

    Explore More
    ::探索更多

    1. Explain how the graph of a function can help you determine whether it is a one-to-one function.
    ::1. 解释一个函数的图形如何帮助您确定它是否为一对一函数。

    2. Provide three examples of one-to-one functions, and explain how you know that they are one-to-one functions.
    ::2. 提供一对一职能的三个实例,并解释你如何知道这些职能是一对一职能。

    3. Provide three examples of functions that are not one-to-one functions, and explain how you know that they are not one-to-one functions. 
    ::3. 提供三个并非一对一职能的职能实例,并解释你如何知道这些职能不是一对一职能。

    4. Are all strictly increasing functions one-to-one? How about strictly decreasing functions? (For strictly increasing or strictly decreasing functions, the  y -values cannot be equal.)
    ::4. 是否所有职能都是一对一严格增加? 如何严格减少职能? (对于严格增加或严格减少的职能,Y值不能相等。 )

    Answers for Review and Explore More Problems
    ::回顾和探讨更多问题的答复

    Please see the Appendix.
    ::请参看附录。