Course: 11.3. 反向函数 | The Way To Learn

Section outline

Select section General

Collapse Expand
General

Collapse all Expand all
- Select activity 新闻通告
  
  新闻通告 Forum

反反函数

The bill for a particular plumber can be modeled by the function $\begin{aligned} y = 50 x + 75 \end{aligned}$ , where $\begin{aligned} x \end{aligned}$ is the number of hours worked and $\begin{aligned} y \end{aligned}$ is the billed amount. If the bill is $250, how many hours did the plumber work for this job?
::特定水管工的账单可以用 y= 50x+75 的函数建模, 其中x是工作小时数,y是账单金额。如果账单是250美元,水管工为这项工作工作了多少小时?

Notice that we start with the value of $\begin{aligned} y \end{aligned}$ and have to find the value of $\begin{aligned} x \end{aligned}$ . We will have to undo all of the operations of the function to find the number of hours. Instead of doing this with each specific value of $\begin{aligned} y \end{aligned}$ , we can generalize this by finding the inverse function. We discuss how to do that in this section.
::请注意, 我们从 y 值开始, 必须找到 x 值。我们不得不撤销函数的所有操作来查找小时数。与其用 y 的每个具体值来这样做, 我们可以通过找到反向函数来概括这一点。我们在本节中讨论如何做到这一点。

lesson content

What Is an Inverse Function?
::什么是反向函数?

An inverse function undoes all of the operations of the original function. Let's consider an example.
::反向函数会取消原函数的所有操作。让我们来举一个例子。

C onsider $\begin{aligned} f (x) = y = 2 x - 3 \end{aligned}$ as the original function. When we put a value in for $\begin{aligned} x \end{aligned}$ , say $\begin{aligned} x = 7 \end{aligned}$ , we multiply it by 2 and then subtract 3: $\begin{aligned} y = f (7) = 2 (7) - 3 = 14 - 3 = 11 \end{aligned}$ .
::将 f( x) =y= 2x- 3 视为原始函数。当我们给 x 下一个值时, 比如 x= 7, 我们乘以 2, 然后减去 3 : y= f(7)= 2(7)- 3= 14- 3= 11 。

If we started with the output of 11 and wanted to get back to the original value of 7, we could undo all of the operations of $\begin{aligned} y \end{aligned}$ . First, we could add 3 to undo the operation of subtracting by 3, and since that was the last operation performed, $\begin{aligned} 11 + 3 = 14 \end{aligned}$ . Then we could do the inverse operation of multiplying by 2, dividing by 2: $\begin{aligned} 14 \div 2 = 7 \end{aligned}$ . This process of adding 3 and dividing by 2 got us back to our original input, 7.
::如果我们从11的输出开始,想要回到7的原始值, 我们就可以取消y的所有操作。首先, 我们可以增加3来取消3减去3的操作, 并且由于这是最后一次执行的操作, 11+3=14。然后我们可以做乘以2的反操作, 乘以2, 乘以2: 14+2=7。增加3和除以2的过程让我们回到了原来的输入, 7。

\begin{aligned} Start f : & End f : \\ x = 7 & ⟶ 2 \times 7 = 14 & ⟶ 14 - 3 = 11 & ⟶ y = 11 \\ End f^{- 1} : & Start f^{- 1} : \\ y = 7 & ⟵ 14 \div 2 = 7 & ⟵ 11 + 3 = 14 & ⟵ x = 11 \\ input of f is & \times and \div are & + and - are & input of f^{- 1} is \\ output of f^{- 1} & inverse operations & inverse operations & output of f \end{aligned}

::开始 f: 开始 f: x= 7\\\\\ 2x7= 14\ _14 - 3=11\ y= 11End f-1: start f-1: y= 7\\\\\ 14\\ 2= 7\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\ f 输入F 输入F - f- f- f- f exexexexexin 输出的 f- f- inver verver 操作输出

Below we formalize this definition.
::下面我们正式确定这一定义。

Inverse Functions
::反反函数

Let $\begin{aligned} f \end{aligned}$ be a one-to-one function. Then for the inverse function, $\begin{aligned} f^{- 1}, \end{aligned}$ %3Dx%2C"> $\begin{aligned} f^{- 1} (y) = x, \end{aligned}$ if and only if $\begin{aligned} f (x) = y \end{aligned}$ .
::使 f 成为一对一的函数。然后对于逆函数, f-1, f-1, f-1=x, 只有当 f(x)=y 时才使用。

WARNINGS
::警告

$\begin{aligned} - 1 \end{aligned}$ is not an exponent. In the vast majority of cases, $\begin{aligned} f^{- 1} (x) \neq \frac{1}{f (x)} \end{aligned}$ . However, any other power of $\begin{aligned} f \end{aligned}$ would be written this way. For example, $\begin{aligned} f^{2} (x) = f (x) \cdot f (x) \end{aligned}$ . To raise $\begin{aligned} f \end{aligned}$ to the $\begin{aligned} - 1 \end{aligned}$ power, write $\begin{aligned} [f (x)]^{- 1} . \end{aligned}$
::在绝大多数情况下, f-1(x) 1f(x) 。但是, 任何其他f的权力都会这样写。例如, f2(x) = f(x) = f(x) f(x) f(x) 。要将 f 提升到 - 1 的功率, 请写 [f(x)]-1 。

We read $\begin{aligned} f^{- 1} (x) \end{aligned}$ as " f inverse of x, " not as " f to the negative one of x ."
::我们把f-1(x)改为“x的反面”,而不是“f至x的负面。”

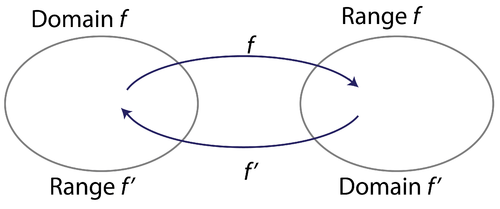
Notice two concepts here. First, the domain of the original function becomes the range of the inverse function, and the range of the original function becomes the domain of the inverse function because the inputs, $\begin{aligned} x \end{aligned}$ , and the outputs, $\begin{aligned} y \end{aligned}$ , switch roles . Also, notice that $\begin{aligned} f \end{aligned}$ and $\begin{aligned} f^{- 1} \end{aligned}$ are inverses of each other. The image below shows these relationships.
::在此注意两个概念。首先, 原始函数的域成为反函数的范围, 而原始函数的域则成为反函数的范围, 因为输入、 x 和输出、 y、交换角色。另外, 注意 f 和 f-1 是彼此的反函数。下面的图像显示这些关系。

lesson content

How to Find Inverse Functions
::如何查找反反函数

Example 1
::例1

Below is a table that relates five states to the order in which they entered the union of the United States. This is a function. Also, notice it is a one-to-one function. Find the inverse function.
::下面的表格将五个州与它们加入美国联盟的顺序联系起来。这是一个函数。另外,通知是一对一的函数。查找反函数。

State	Order
Delaware	1
Pennsylvania	2
New Jersey	3
Georgia	4
Connecticut	5

Solution: To find the inverse function, the outputs become the inputs and the inputs become the outputs. The inverse function is below.
::解决方案:为查找反向函数,产出成为投入,投入成为产出。反向函数如下。

Order	State
1	Delaware
2	Pennsylvania
3	New Jersey
4	Georgia
5	Connecticut

Example 2
::例2

Find the inverse function for the following functions:
::查找下列函数的反函数:

a.
::a 。

b.
::b. b. 数据

Solution:
::解决方案 :

a. For the inverse function, we need to map from set B, the outputs of the original function, to set A, the inputs of the original function. The picture with the corresponding set of ordered pairs of the inverse function is below.
::a. 对于反向函数,我们需要从原函数的输出B组绘制地图,然后将原函数的输入A组绘制图。反向函数对应的一对定序图见下文。

b. As in part a, we map from set B to set A. However, when we do this, the inverse "function" is not a function: $\begin{aligned} x \end{aligned}$ maps to $\begin{aligned} b \end{aligned}$ and $\begin{aligned} c \end{aligned}$ . There is no inverse function.
::b. 作为a部分,我们从B区绘制B区地图到A区地图。然而,当我们这样做时,反“功能”不是一个函数:x地图到b和c区地图。没有反函数。

This example shows an important point. Notice that part a is a one-to-one function; however, part b is not one-to-one. It is necessary for functions to be one-to-one functions to find an inverse function.
::此示例显示一个重要点。注意一个部分是一个一对一的函数; 但是, b部分不是一对一的函数。函数必须是一对一的函数, 才能找到一个反函数。

Example 3
::例3

Find the inverse function for $\begin{aligned} S = {(6, - 1), (- 2, - 5), (- 3, 4), (0, 3), (2, 2)} . \end{aligned}$ Identify the domain and range of $\begin{aligned} S \end{aligned}$ and $\begin{aligned} S^{- 1} . \end{aligned}$
::查找 S( 6, 1), (2, 5), (3, 4), (0, 3), (2, 2)} 的反函数。确定 S 和 S-1 的域域和范围。

Solution: Since this function is one-to-one, we can find the inverse function by switching the $\begin{aligned} x \end{aligned}$ - and $\begin{aligned} y \end{aligned}$ -coordinates. The inverse function is $\begin{aligned} S^{- 1} = {(- 1, 6), (- 5, - 2), (4, - 3), (3, 0), (2, 2)} . \end{aligned}$
::解答: 由于此函数是一对一, 我们可以通过切换 X 和 Y 坐标找到反函数。反函数是 S-1 {( 1 ) {( 1 ) {( 6 ) , ( 5 ) {( 4 ) {( 4 ) {( 3 ) {( 3 ) {(2 )} 。

The blue points are all the points in $\begin{aligned} S, \end{aligned}$ and the red points are all the points in $\begin{aligned} S^{- 1} . \end{aligned}$ When we graph the points in the function and its inverse, we can see that the points are reflected over the line $\begin{aligned} y = x \end{aligned}$ . All functions and their inverses have this property.
::蓝色点是S中的所有点,红色点是S-1中的所有点。当我们绘制函数及其反向的点时,我们可以看到这些点在 y=x 线上得到反映。所有函数及其反向都有此属性。

lesson content

If we were to fold the graph along $\begin{aligned} y = x \end{aligned}$ , each point in $\begin{aligned} S^{- 1} \end{aligned}$ should align with the original point from $\begin{aligned} S \end{aligned}$ . The point $\begin{aligned} (2, 2) \end{aligned}$ lies on this line, so it aligns with itself .
::如果我们沿着 y=x 折叠图表, S-1 中的每个点应该与 S 的原点一致。点 (2, 2) 位于这条线上, 所以它与它自己一致。

As was stated above in the definition, the inverse relation switched the domain and range of the original function.
::正如上文定义中所述,反向关系改变了原有功能的域和范围。

Domain of $\begin{aligned} S \end{aligned}$ : $\begin{aligned} x \in {6, - 2, - 3, 0, 2} \end{aligned}$
::S域域: x6, 2, 2, 3, 3, 0, 2}

Range of $\begin{aligned} S \end{aligned}$ : $\begin{aligned} y \in {- 1, - 5, 4, 3, 2} \end{aligned}$
::S范围:y-1,-5,4,4,3,2}

Domain of $\begin{aligned} S^{- 1} \end{aligned}$ : $\begin{aligned} x \in {- 1, - 5, 4, 3, 2} \end{aligned}$
::S-1域域: x-1,-5,4,4,3,2}

Range of $\begin{aligned} S^{- 1} \end{aligned}$ : $\begin{aligned} y \in {6, - 2, - 3, 0, 2} \end{aligned}$
::S-1范围:y6, 2, 3, 3, 0, 2}

Example 4
::例4

Find the inverse of $\begin{aligned} f (x) = \frac{2}{3} x - 1. \end{aligned}$
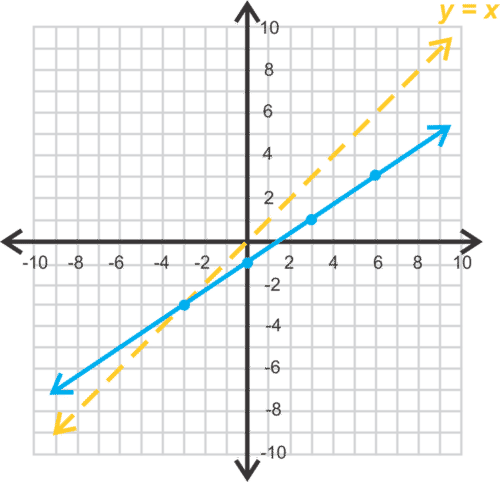
::查找 f( x) =23x- 1 的反方向。

Solution: This function is a line, and it is not a horizontal line, so it is one-to-one. We can find the inverse graphically using the symmetry of a function and its inverse across the line $\begin{aligned} y = x \end{aligned}$ . First, we graph the function $\begin{aligned} f (x) = \frac{2}{3} x - 1 \end{aligned}$ .
::解析 : 此函数是一个线条, 它不是一个水平线, 所以它是一个对一的线条。我们可以用函数的对称和横跨 y=x 线的反对法来找到反向图。首先, 我们绘制函数 f( x) = 23x - 1 的图示。

lesson content

Notice the points on the function (blue line). We can map these points across $\begin{aligned} y = x \end{aligned}$ by switching their $\begin{aligned} x \end{aligned}$ - and $\begin{aligned} y \end{aligned}$ -values. (You c an also fold the graph along $\begin{aligned} y = x \end{aligned}$ and trace the reflection.)
::注意函数( 蓝线) 上的点。我们可以通过切换这些点的 x 和 y 值来绘制这些点的 y =x 。 (您也可以沿着 y =x 折叠图形并跟踪反射。)

lesson content

The red line in the graph is the inverse of $\begin{aligned} f (x) = \frac{2}{3} x - 1 \end{aligned}$ . If we consider the points $\begin{aligned} (- 1, 0) \end{aligned}$ and $\begin{aligned} (1, 3) \end{aligned}$ , we can find the slope and then we can use $\begin{aligned} (- 1, 0) \end{aligned}$ to find the $\begin{aligned} y \end{aligned}$ -intercept in slope-intercept form.
::图表中的红线是 f(x) = 23x- 1 的反方向。如果我们考虑点数( 1- 0) 和 (1, 3) , 我们就可以找到斜度, 然后我们就可以使用 (-1,0) 来在斜度界面中找到 y 界面。

\begin{aligned} m & = \frac{y_{2} - y_{1}}{x_{2} - x_{1}} \\ = \frac{3 - 0}{1 - (- 1)} \\ = \frac{3}{2} \\ f^{- 1} (x) & = \frac{3}{2} x + b \\ 0 & = \frac{3}{2} (- 1) + b \\ \frac{3}{2} & = b \end{aligned}

::my2-y1x2-x1=3-01-(-1)=32f-1(x)=32x+b0=32(-1)+b32=b

The equation of the inverse is $\begin{aligned} f^{- 1} (x) = \frac{3}{2} x + \frac{3}{2} . \end{aligned}$
::倒数方程式为 f-1(x) = 32x+32。

You may have noticed that the slopes of $\begin{aligned} f \end{aligned}$ and $\begin{aligned} f^{- 1} \end{aligned}$ are reciprocals of each other. This will always be the case for linear functions and their inverses.
::你可能注意到F和F-1的斜坡是相互对等的。线性函数及其反射总是这样。

How to Find an Inverse Function From a Graph
::如何从图表中查找反向函数

Functions and their inverses are symmetric about the line $\begin{aligned} y = x \end{aligned}$ .
::函数及其反函数与 y=x 线对称。

We can find points on the graph of the inverse function by switching the $\begin{aligned} x \end{aligned}$ - and $\begin{aligned} y \end{aligned}$ -coordinates of points on the original function. Point $\begin{aligned} (a, b) \end{aligned}$ on the graph of the function corresponds to the point $\begin{aligned} (b, a) \end{aligned}$ on the graph of the inverse function.
::我们可以通过切换原函数上的点的 X 和 Y 坐标,在反函数图中找到反函数图中的点。函数图中的点(a,b)与反函数图中的点(b,a)对应。

by Mathispower4u discusses this relationship between the graph and the graph of the inverse function.
::在 Mathispower4u 中讨论图形与反函数图之间的关系。

Example 5
::例5

Find the inverse of $\begin{aligned} f (x) = \frac{2}{3} x - 1 \end{aligned}$ algebraically, and check that the inverse function is correct.
::查找 f( x) =23x- 1 的反义代数,并检查反函数是否正确。

Solution: There is also an algebraic approach to finding the inverse of a function. Let's repeat Example 4 using algebra.
::解答: 还有一个代数法来查找函数的反向。让我们用代数重复例4。

Step 1: Determine if the function is one-to-one.
::第1步:确定该函数是否一对一。

In Example 4, we established that the function was one-to-one.
::在例4中,我们确定该职能是一对一。

Step 2: Change $\begin{aligned} f (x) \end{aligned}$ to $\begin{aligned} y \end{aligned}$ . This is largely to make the algebra easier to follow.
::第2步:将f(x)改为y。这主要是为了便于代数的采用。

\begin{aligned} y = \frac{2}{3} x - 1 \end{aligned}

::y=23x-1

Step 3: Switch $\begin{aligned} x \end{aligned}$ and $\begin{aligned} y \end{aligned}$ . This would normally be quite an unusual step in algebra, but we are doing this because the roles of the domain and the range of the original function are switching with the inverse function.
::第3步:切换 X 和 y。代数中这通常是一个非常不寻常的步骤, 但我们这样做是因为域的作用和原始函数的范围正与反函数转换。

\begin{aligned} x = \frac{2}{3} y - 1 \end{aligned}

::x=23y-1

Step 4: Solve for $\begin{aligned} y \end{aligned}$ .
::步骤4:解决y。

\begin{aligned} x & = \frac{2}{3} y - 1 \\ x + 1 & = \frac{2}{3} y \\ \frac{3}{2} (x + 1) & = \frac{3}{2} \cdot (\frac{2}{3} y) \\ \frac{3}{2} x + \frac{3}{2} & = y \end{aligned}

::x=23y- 1x+1=23y32( x+1)=32&( 23y) 32x+32=y

Step 5: Replace $\begin{aligned} y \end{aligned}$ with $\begin{aligned} f^{- 1} (x) \end{aligned}$ .
::第5步:将y改为f-1(x)。

\begin{aligned} f^{- 1} (x) = \frac{3}{2} x + \frac{3}{2} \end{aligned}

::f-1(x)=32x+32

Step 6: To check inverse functions, we need to perform two compositions and see if what we input, usually $\begin{aligned} x \end{aligned}$ , is what we output. (To review composition of functions, see the section entitled "Composition of Functions" earlier in this book.)
::步骤6:为检查反向函数,我们需要执行两种组成,并看看我们输入的通常是x,是否是我们输出的。 (要审查函数的构成,请见本书前面题为“职能组合”的一节。 )

The 1st composition is $\begin{aligned} (f \circ f^{- 1}) (x) \end{aligned}$ . Here, we will do all of the operations of $\begin{aligned} f^{- 1} \end{aligned}$ and then undo them with all of the operations of $\begin{aligned} f \end{aligned}$ . This should result in $\begin{aligned} x \end{aligned}$ .
::第一个构成是 (ff-1)(x) 。在这里, 我们将完成 F-1 的所有操作, 然后用 f 的所有操作来解除它们。这将导致 x 。

\begin{aligned} (f \circ f^{- 1}) (x) = f (f^{- 1} (x)) & = f (\frac{3}{2} x + \frac{3}{2}) \\ = \frac{2}{3} (\frac{3}{2} x + \frac{3}{2}) - 1 \\ = \frac{2}{3} \cdot \frac{3}{2} x + \frac{2}{3} \cdot \frac{3}{2} - 1 \\ = x + 1 - 1 \\ = x \end{aligned}

f*f-1(x)=f(f-1(xx))=f(32x+32)=23(32x+32)=23(32x+32)-1=23_32x+23_321=x1=x+1-1=1=x=x

Since we can compose functions in one direction, get $\begin{aligned} x \end{aligned}$ , and yet not have correct inverse functions, we need to perform a 2nd composition, $\begin{aligned} (f^{- 1} \circ f) (x) \end{aligned}$ . Here, we will do all of the operations of $\begin{aligned} f \end{aligned}$ and then undo them with $\begin{aligned} f^{- 1} \end{aligned}$ . Again, we want a result that is our input, $\begin{aligned} x \end{aligned}$ .
::由于我们可以在一个方向组成函数, 获得 x, 但却没有正确的反函数, 我们需要执行第二个组成, (f-1f) (x) 。在这里, 我们将完成 f 的所有操作, 然后用 f-1 来取消它们。我们再次想要一个结果, 也就是输入, x 。

\begin{aligned} (f^{- 1} \circ f) (x) = f^{- 1} (f (x)) & = f^{- 1} (\frac{2}{3} x - 1) \\ = \frac{3}{2} (\frac{2}{3} x - 1) + \frac{3}{2} \\ = \frac{3}{2} \cdot \frac{2}{3} x - \frac{3}{2} \cdot 1 + \frac{3}{2} \\ = x - \frac{3}{2} + \frac{3}{2} \\ = x \end{aligned}

f-1f(x) = f-1 (f(x)) = f-1 (23x- 1) = 32(23x-1) = 32(23x-1) +32= 3223x- 32_1) +32= 32_23x- 32_1+32=x-32+32=x- 32+32=x

This algebraic method can a lso be used to find an inverse .
::这种代数法也可以用来寻找反向。

How to Find an Inverse Function Algebraically
::如何查找反反函数代数

1. Determine if the function is one-to-one.
::1. 确定该职能是否一对一。

2. If the function uses function notation, replace $\begin{aligned} f (x) \end{aligned}$ with $\begin{aligned} y \end{aligned}$ .
::2. 如果函数使用函数符号,f(x)改为y。

3. Switch $\begin{aligned} x \end{aligned}$ and $\begin{aligned} y \end{aligned}$ .
::3. 交换x和y。

4. Solve for $\begin{aligned} y \end{aligned}$ .
::4. 解决y.

5. If using function notation, denote the new function as $\begin{aligned} f^{- 1} (x) \end{aligned}$ .
::5. 如果使用函数符号,则表示新的函数为f-1(x)。

6. Check that the two functions are inverses of each other by verifying $\begin{aligned} (f \circ f^{- 1}) (x) = x \end{aligned}$ and $\begin{aligned} (f^{- 1} \circ f) (x) = x \end{aligned}$ .
::6. 通过核查(ff-1(x)=x和(f-1f(x)=x)=x,检查这两个功能是相互反相的。

by CK-12 describes how to check whether functions are inverses by composing them.
::使用 CK-12 描述如何通过组合来检查函数是否反向。

Example 6
::例6

Solution: First, we can find the inverse function for this linear function.
::解答: 首先, 我们可以找到这个线性函数的反函数。

\begin{aligned} y & = 50 x + 75 \\ x & = 50 y + 75 \\ x - 75 & = 50 y \\ \frac{x - 75}{50} & = y \\ y^{- 1} & = \frac{1}{50} x - \frac{3}{2} \end{aligned}

::y=50x+75x=50y+75x-75=50yx-7550=yyy-1=150x-32

Now that we have an inverse function, we can check it by doing two compositions.
::既然我们有一个反向函数, 我们可以通过做两种组成来检查它。

\begin{aligned} y \circ y^{- 1} & = 50 (\frac{1}{50} x - \frac{3}{2}) + 75 = x - 75 + 75 = x \\ y^{- 1} \circ y & = \frac{1}{50} (50 x + 75) - \frac{3}{2} = x + \frac{3}{2} - \frac{3}{2} = x \end{aligned}

::yy-1=50( 150x-32)+75=x- 75+75=x- 75+75=xy=xy=150( 50x+75)- 32=x32- 32=x

The inverse function is correct. Now we can use the inverse function to find the number of hours worked for a bill of $250.
::反函数是正确的。现在我们可以使用反函数来查找账单250美元的工时数。

\begin{aligned} y^{- 1} = \frac{1}{50} (250) - \frac{3}{2} = 5 - \frac{3}{2} = \frac{10}{2} - \frac{3}{2} = \frac{7}{2} = 3 \frac{1}{2} \end{aligned}

The customer was billed for

\begin{aligned} 3 \frac{1}{2} \end{aligned}

hours of work.
::y-1=150(250)-32=5-32=102-32=72=312

Since we have an inverse function, we can now find how many hours the plumber worked given any bill amount.
::由于我们有一个反向功能,我们现在可以找到水管工工作了多少小时,给任何帐单金额。

$\begin{aligned} $ 400 : y^{- 1} = \frac{1}{50} (400) - \frac{3}{2} = 8 - \frac{3}{2} = \frac{13}{2} = 6 \frac{1}{2} hours \\ $ 100 : y^{- 1} = \frac{1}{50} (100) - \frac{3}{2} = 2 - \frac{3}{2} = \frac{1}{2} hour \end{aligned}$

::400:y-1=150(400-32=8-32=132=612小时100:y-1=150(100)-32=2-32=12小时

Example 7
::例7

Find the inverse of the following one-to-one function, $\begin{aligned} f (x) = \frac{3 x + 13}{2 x - 11} \end{aligned}$ . Note any restrictions to the domain of the inverse function.
::查找以下一对一函数的倒数,f(x)=3x+132x-11。请注意对反函数域的任何限制。

Solution: This function may be more complicated than the previous functions, but the steps are the same. Since we are given that the function is one-to-one, we can replace $\begin{aligned} f (x) \end{aligned}$ with $\begin{aligned} y \end{aligned}$ and then switch $\begin{aligned} x \end{aligned}$ and $\begin{aligned} y \end{aligned}$ . The latter means that every $\begin{aligned} x \end{aligned}$ becomes a $\begin{aligned} y, \end{aligned}$ and every $\begin{aligned} y \end{aligned}$ becomes an $\begin{aligned} x \end{aligned}$ .
::解析 : 此函数可能比先前的函数更加复杂, 但步骤是一样的。由于我们给出了一对一的函数, 我们可以用 y 替换 f( x) , 然后切换 x 和 y 。后者意味着每个 x 变成 y, 而每个 y 变成 x 。

\begin{aligned} f (x) & = \frac{3 x + 13}{2 x - 11} \\ y & = \frac{3 x + 13}{2 x - 11} \\ x & = \frac{3 y + 13}{2 y - 11} \end{aligned}

::f( x) = 3x+132x- 11y= 3x+132x- 11x= 3y+132y- 11

Now we have to solve for $\begin{aligned} y \end{aligned}$ ; however, there are two $\begin{aligned} y \end{aligned}$ 's in the equation. Let's m ultiply both sides by $\begin{aligned} 2 y - 11 \end{aligned}$ to eliminate the fraction. Next, we can rearrange the terms to get both terms with $\begin{aligned} y \end{aligned}$ on one side and everything else on the other side.
::现在我们必须解决y的问题; 但是, 方程中有两个y's。让我们将两边乘以 2y- 11 来消除分数。接下来, 我们可以重新安排条件, 以获得 y 和 y 的一面条件, 和 other 的一面条件。

\begin{aligned} (2 y - 11) (x) & = \frac{3 y + 13}{2 y - 11} (2 y - 11) & eliminate the fraction \\ 2 x y - 11 x & = 3 y + 13 \\ 2 x y - 3 y - 11 x & = 13 & terms with y on the same side \\ 2 x y - 3 y & = 11 x + 13 & terms without y on the same side \end{aligned}

2y-11)(x)=3y+132y+132y-11(2y-11) =3y=3y+132xy-3y=3y+132xy-3y-11x=13Texts 与 Y 在同一侧面2xy-3y=11x+13Texts没有 Y 在同一侧面

Factor out the $\begin{aligned} y \end{aligned}$ on the left side of the equation , and d ivide both sides by $\begin{aligned} 2 x - 3 \end{aligned}$ to isolate $\begin{aligned} y \end{aligned}$ .
::乘以方程左侧的y, 将两边除以 2x- 3, 隔开 y 。

\begin{aligned} y (2 x - 3) & = 11 x + 13 \\ y & = \frac{11 x + 13}{2 x - 3} \end{aligned}

::y( 2x- 3) =11x+13y=11x+132x- 3

So, the inverse of $\begin{aligned} f (x) = \frac{3 x + 13}{2 x - 11}, x \neq \frac{11}{2} \end{aligned}$ is $\begin{aligned} f^{- 1} (x) = \frac{11 x + 13}{2 x - 3}, x \neq \frac{3}{2} \end{aligned}$ .
::因此, f( x) =3x+132x- 11,x* 112 的反义为 f-1( x) = 11x+132x- 3,x* 32。

We can check these by composing them. This will result in a complex fraction in both compositions. Recall that one way to simplify complex fractions is to multiply all of the terms by the least common denominator. We will use that approach here.
::我们可以通过编组它们来检查它们。这将在两种组成中造成一个复杂的分数。提醒大家注意, 简化复杂分数的一种方法是将所有术语乘以最小的公分母。我们将在此使用这个方法。

\begin{aligned} (f \circ f^{- 1}) (x) = f (f^{- 1} (x)) & = f (\frac{11 x + 13}{2 x - 3}) \\ = \frac{3 (\frac{11 x + 13}{2 x - 3}) + 13}{2 (\frac{11 x + 13}{2 x - 3}) - 11} \\ = \frac{(3 (\frac{11 x + 13}{2 x - 3}) + 13) \cdot (2 x - 3)}{(2 (\frac{11 x + 13}{2 x - 3}) - 11) \cdot (2 x - 3)} \\ = \frac{3 (\frac{11 x + 13}{2 x - 3}) \cdot (2 x - 3) + 13 (2 x - 3)}{2 (\frac{11 x + 13}{2 x - 3}) \cdot (2 x - 3) - 11 (2 x - 3)} \\ = \frac{3 (11 x + 13) + 13 (2 x - 3)}{2 (11 x + 13) - 11 (2 x - 3)} \\ = \frac{33 x + 39 + 26 x - 39}{22 x + 26 - 22 x + 33} \\ = \frac{59 x}{59} \\ = x \end{aligned}

The approach for the composition in the opposite order is similar.
:

f*f-1(x)=f(f-1(xx))=f(11x+132x-3)=3(11x+132x-3)+132(11x-132x-3)+132x-3)(11x+132x-3)-11=3(3(3xxx-3))(2(11x-132x-3)-(2x-3)(2xx-132x-3)=(11x+132x-3)=(3x3)+13(11x+132x-3)+132x-3)(11x-132x-3)+132x-3)(11x-11=(3xx-3)=(3x+132x-3)+(3x-3)+(2x-3(3x)(2x))(2(11x-132x-132x-3)+(2x-3)(2(2xx-132x-3)(2(2(2x))(2xx+132x-132x-3(3))(2x-)(2x+33x+33xx-39x-39xx-39x-32x=59x=xxxxxxxxxxxx)x)x(3)x(3)(2x)x的构成相反的相同的相同相近相近不相近不相近不相近。的方法方法。

\begin{aligned} (f^{- 1} \circ f) (x) = f^{- 1} (f (x)) & = f^{- 1} (\frac{3 x + 13}{2 x - 11}) \\ = \frac{11 (\frac{3 x + 13}{2 x - 11}) + 13}{2 (\frac{3 x + 13}{2 x - 11}) - 3} \\ = \frac{(11 (\frac{3 x + 13}{2 x - 11}) + 13) \cdot (2 x - 11)}{(2 (\frac{3 x + 13}{2 x - 11}) - 3) \cdot (2 x - 11)} \\ = \frac{11 (\frac{3 x + 13}{2 x - 11}) \cdot (2 x - 11) + 13 (2 x - 11)}{2 (\frac{3 x + 13}{2 x - 11}) \cdot (2 x - 11) - 3 (2 x - 11)} \\ = \frac{11 (3 x + 13) + 13 (2 x - 11)}{2 (3 x + 13) - 3 (2 x - 11)} \\ = \frac{33 x + 143 + 26 x - 143}{6 x + 26 - 6 x + 33} \\ = \frac{59 x}{59} \\ = x \end{aligned}

f-1***f(x)=f-1(f(f)(x))=f-1(f)(3x+132x-11)=f-1(3x+132x-11)=11(3x+132x-11)=11(3x+132x-11)+132x-11)(3x-132x-11)+132x-11)=13(3x+132x-132x-11)=11(3x+132x-132x-11)=11(3x+132x-11)+132x-11)(3x-132x-132x-11)+132(3x-132x-11)=3=11(3x+13)+13(2x-11)(3x+13)=3(2x-11)=33x+143+26x-1436x+266x+33=59x=x

by Mathispower4u summarizes the techniques in this section.
::由 Mathispower4u 总结本节的技术。

Example 8
::例8

Find the inverse of $\begin{aligned} f (x) = x^{2} + 2 \end{aligned}$ .
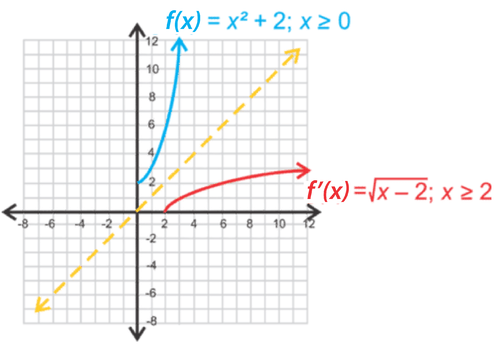
::查找 f( x) =x2+2 的反义。

Solution: First we need to determine if $\begin{aligned} f \end{aligned}$ is a one-to-one function. In the graph below, you can see that it fails the horizontal line test, so it is not one-to-one. If we wanted to find the inverse by reflecting $\begin{aligned} f \end{aligned}$ over $\begin{aligned} y = x \end{aligned}$ , it would be a parabola on its side, which is not a function because it fails the vertical line test.
::解决方案 : 首先我们需要确定 f 是否是一个一对一的函数。在下图中, 您可以看到它失败了水平线测试, 所以它不是一对一。如果我们想通过反射 f 反射 y=x 来找到反向, 它将是一个侧面的抛物线, 这不是一个函数, 因为它失败了垂直线测试。

What we do in these cases is limit the domain to a part of the graph that is one-to-one. If we only consider $\begin{aligned} f \end{aligned}$ for $\begin{aligned} x \geq 0 \end{aligned}$ , then we have a one-to-one piece because half of the parabola is one-to-one. We call this a domain restriction, and it is what we have to do to find inverse functions for original functions that are not one-to-one.
::在这些情况下,我们要做的是将域限为图中的一对一的一部分。如果我们只考虑 x°0 f,那么我们就会有一个一对一的字符,因为有一半的抛物线是一对一。我们称之为域限制,这是我们为原始函数找到反函数所必须做的,而不是一对一。

After we restrict the domain, we can proceed as usual. Here, we reflect half of the parabola over the line $\begin{aligned} y = x \end{aligned}$ to get the inverse function $\begin{aligned} f^{- 1} (x) = \sqrt{x - 2} \end{aligned}$ .
::在限制域后, 我们可以照常进行。这里, 我们映射了 y=x 线上半个抛物线, 以获得 f-1( x) =x-2 的反函数。

lesson content

We could also approach this algebraically as well.
::我们还可以从代数的角度来看待这个代数。

\begin{aligned} f (x) & = x^{2} + 2 \\ y & = x^{2} + 2 \\ x & = y^{2} + 2 \\ x - 2 & = y^{2} \\ \pm \sqrt{x - 2} & = y \\ f^{- 1} (x) & = \sqrt{x - 2} & choose positive square root \\ because of domain restriction \end{aligned}

::f(x) =x2+2y=x2+2x=x2+2x=y2+2x-2=y2_x-2=y2_x-2=yf-1(x) =x-2choose正正平方根,因为域限制

When we check the inverses, we have
::当我们检查逆反,我们有

\begin{aligned} f \circ f^{- 1} & = \sqrt{(x^{2} + 2) - 2} & f^{- 1} \circ f = {\sqrt{x - 2}}^{2} + 2 \\ = \sqrt{x^{2}} & and & = x - 2 + 2 \\ = x & = x \end{aligned}

::f- 1 = (x2+2) - 2f- 1 @ @ @ f=x- 22+2=x2and=x-2+2=x=x

How to Find an Inverse Function With a TI-83/84
::如何用 TI-83/84 查找反函数

1. Enter the original function under Y= .
::1. 在Y=下输入原始函数。

2. Press 2nd and then PRGM to get the DRAW menu.
::2. 按第二版,然后按PRGM键,以获得DRAW菜单。

3. Choose DrawInv in the menu. (You may need to scroll down.)
::3. 在菜单中选择 DrawInv。 (可能需要向下滚动。)

4. Now that we have the command, we need to choose the function. Press VARS and use the right arrow to choose Y-VARS .
::4. 既然我们有了命令,我们需要选择函数,按VARS键,用正确的箭头选择Y-VARS。

5. Select Function and then choose the function number where you entered the function.
::5. 选择函数,然后选择输入函数的函数编号。

6. Now you should have a command and a function. Press ENTER and the graph will appear in the window.
::6. 现在,你应该有一个命令和一个函数。按 ENTER 键和图将显示在窗口中。

Summary
::摘要

The domain of $\begin{aligned} f \end{aligned}$ is the range of $\begin{aligned} f^{- 1} \end{aligned}$ and the range of $\begin{aligned} f \end{aligned}$ is the domain of $\begin{aligned} f^{- 1} . \end{aligned}$
::f 的域是 f-1 的域, f 的域是 f-1 的域。

Functions and their inverses are symmetric about the line $\begin{aligned} y = x \end{aligned}$ .
::函数及其反函数与 y=x 线对称。

To find an inverse function algebraically, determine that the function is one-to-one, switch the variables for the input and the output (usually $\begin{aligned} x \end{aligned}$ for the input and $\begin{aligned} y \end{aligned}$ for the output), and solve for the output variable.
::要找到反向函数代数,确定函数为一对一,切换输入和输出的变量(输入和输出通常为x,输出为y),并解析输出变量。

To check inverse functions, compose the function and its inverse twice to see if the result is $\begin{aligned} x \end{aligned}$ —that is, $\begin{aligned} (f \circ f^{- 1}) (x) = x \end{aligned}$ and $\begin{aligned} (f^{- 1} \circ f) (x) = x \end{aligned}$ .
::要检查反函数,请将函数及其反函数组成两次以查看结果是否为 x - 即 (ff-1)(x)=x 和 (f-1f (x)=x) 。

If a function is not one-to-one, restrict its domain to a section of the graph that is one-to-one.
::如果函数不是一对一,则将其域限为一对一的图形部分。

Review
::回顾

Write or graph the inverses of the functions below. State whether or not the inverse is a function.
::写入或图形以下函数的反函数。请说明反函数是否为函数。

1. $\begin{aligned} {(2, 3), (- 4, 8), (- 5, 9), (1, 1)} \end{aligned}$

2. $\begin{aligned} {(9, - 6), (8, - 5), (7, 3), (4, 3)} \end{aligned}$

Find the inverses of the functions below algebraically. Note any restrictions to the domain of the inverse functions.
::查找代数下函数的反函数。请注意对反函数区域的任何限制。

4. $\begin{aligned} f (x) = 6 x - 9 \end{aligned}$
::4. f(x)=6x-9

5. $\begin{aligned} f (x) = \frac{1}{4 x + 3} \end{aligned}$
::5. f(x)=14x+3

6. $\begin{aligned} f (x) = \sqrt{x + 7} \end{aligned}$
::6. f(x)=x+7

7. $\begin{aligned} f (x) = x^{2} + 5 \end{aligned}$
::7. f(x)=x2+5

8. $\begin{aligned} f (x) = x^{3} - 11 \end{aligned}$
::8. f(x)=x3-11

9. $\begin{aligned} f (x) = \sqrt[5]{x + 16} \end{aligned}$
::9.f(x)=x+165

10. $\begin{aligned} f (x) = \frac{x + 7}{x}, x \neq 0 \end{aligned}$
::10. f(x) =x+7x,x=0

11. $\begin{aligned} f (x) = \frac{x}{x - 8}, x \neq 8 \end{aligned}$
::11. f(x) =xxx-8,x8

Determine whether $\begin{aligned} f \end{aligned}$ and $\begin{aligned} g \end{aligned}$ are inverses of each other by checking to see whether finding $\begin{aligned} f \circ g = x \end{aligned}$ or $\begin{aligned} g \circ f = x \end{aligned}$ .
::确定 f 和 g 是彼此的反向, 检查是否找到 fg=x 或 gf=x 。

12. $\begin{aligned} f (x) = \frac{2}{3} x - 14 \end{aligned}$ and $\begin{aligned} g (x) = \frac{3}{2} x + 21 \end{aligned}$
::12. f(x)=23x-14和g(x)=32x+21

13. $\begin{aligned} f (x) = \frac{x + 5}{8} \end{aligned}$ and $\begin{aligned} g (x) = 8 x + 5 \end{aligned}$
::13. f(x)=x+58和g(x)=8x+5

14. $\begin{aligned} f (x) = \sqrt[3]{3 x - 7} \end{aligned}$ and $\begin{aligned} g (x) = \frac{x^{3}}{3} - 7 \end{aligned}$
::14. f(x)=3x-73和 g(x)=x33-7

15. $\begin{aligned} f (x) = \frac{x}{x - 9}, x \neq 9 \end{aligned}$ and $\begin{aligned} g (x) = \frac{9 x}{x - 1} \end{aligned}$
::15.f(x)=xx-9,x9和g(x)=9xx-1

Explore More

::探索更多

1. In many countries, the temperature is measured in degrees Celsius. In the U.S., we typically use degrees Fahrenheit. For travelers, it is helpful to be able to convert from one unit of measurement to the other. The following problem will show you how to do this using an inverse function:
::1. 在许多国家,温度是用摄氏度测量的。在美国,我们通常使用华氏度。对于旅行者来说,能够从一个测量单位转换为另一个测量单位是有益的。以下问题将表明如何使用一个反向函数来做到这一点:

Step 1: The temperature at which water freezes will give us one point on a line in which $\begin{aligned} x \end{aligned}$ represents the degrees in Celsius, and $\begin{aligned} y \end{aligned}$ represents the degrees in Fahrenheit. Water freezes at 0 degrees Celsius and 32 degrees Fahrenheit, so the 1st point is (0, 32). The temperature at which water boils gives us the 2nd point (100, 212), because water boils at 100 degrees Celsius or 212 degrees Fahrenheit ¹ . Use this information to show that the equation to convert from Celsius to Fahrenheit is $\begin{aligned} y = \frac{9}{5} x + 32 \end{aligned}$ or $\begin{aligned} F = \frac{9}{5} C + 32 \end{aligned}$ .
::第一步 1: 水冻结的温度将给我们一个点, 在这条线上 x 代表摄氏度, y 代表华氏度。水冻结在 0 摄氏度和 32 华氏度, 所以第一个点是 (0, 32 ) 。水沸腾的温度给了我们第二个点( 100, 212 ) , 因为水沸腾在 100 摄氏度或 212 华氏度。使用此信息显示, 从摄氏度转换为法氏度的方程式是 y= 95x+32 或 F= 95C+32 。

Step 2: Find the inverse of the equation above by solving for $\begin{aligned} C \end{aligned}$ to derive a formula that will allow us to convert from Fahrenheit to Celsius.
::第2步:通过解决C得出一个公式,让我们从法赫里内特转换成摄氏度,找出上述方程的反面。

Step 3: Determine that your inverse is correct by showing that the composition of the two functions simplifies to either $\begin{aligned} F \end{aligned}$ or $\begin{aligned} C \end{aligned}$ (depending on which one you put into the other).
::第3步:通过显示两个函数的构成简化为F或C(取决于您将哪一个函数简化为另一个函数),确定您的反向正确。

by CK-12 provides a similar problem to the one above.
::CK-12 提供了与上述问题类似的问题。

2. Determine whether the graphs of $\begin{aligned} y = \sqrt{x} \end{aligned}$ and its inverse intersect at the point (4,2).
::2. 确定y=x的图形及其在点(4,2)的反向交叉点(4,2)是否为y=x的图形。

3. Use inverse functions to find the radius of the base of a right circular cone that has a height h = 50 inches, and a volume of 200 cubic inches. (Recall that the formula of the volume V of a right circular cone with height h and radius r is given by $\begin{aligned} V = (1 / 3) π r^{2} h .) \end{aligned}$
::3. 使用反函数查找右圆锥形底部的半径,右圆锥体的高度 h = 50 英寸,体积为 200 立方英寸。 (回顾右圆锥体卷五与高度 h 和半径 r 的公式由 V = (1/3) r2h 给出。)

4. A planet's maximum distance from the sun (in astronomical units) is given by the formula $\begin{aligned} d = p^{\frac{2}{3}} \end{aligned}$ , where p is the period (in years) of the planet's orbit around the sun ² . What is the inverse of this function?
::4. 公式d=p23给出了行星与太阳的最大距离(天文单位),公式d=p23给出了太阳周围行星轨道的周期(年数),p是月数。

5. Show the identity function, $\begin{aligned} y = x \end{aligned}$ , is its own inverse. We call it the identity function because for composition it plays a similar role as 0 for addition, or 1 for multiplication.
::5. 显示身份函数Y=x是其本身的反向函数。我们称它为身份函数,因为就其构成而言,它的作用类似于增加 0 或乘以 1 。

6. Do all linear functions have inverse functions? Try to draw an exception.
::6. 线性函数是否都具有反函数?尝试引出一个例外。

7. An exchange rate for the U.S. dollar to a bitcoin was one U.S. dollar to 0.00082 bitcoins ³ . Write a function that models the exchange of dollars to bitcoins and find the inverse function. What does the inverse function represent? According to this model, how much is 1 bitcoin worth?
::7. 美元兑比特币的汇率是1美元兑0.0082比特币3。写一个函数,模拟美元对比特币的兑换,发现反函数。反函数代表什么?根据这个模型,1比特币的价值是多少?

Answers for Review and Explore More Problems
::回顾和探讨更多问题的答复

Please see the Appendix.
::请参看附录。

PLIX
::PLIX

Try these interactives that reinforce the concepts explored in this section:
::尝试这些强化本节所探讨概念的交互作用 :

Resources
::资源

Please see the Resources tab for additional materials.
::更多信息请访问资源标签。

References
::参考参考资料

1. "Fahrenheit," last edited June 1, 2017,
::1. 2017年6月1日经编辑

2. "Kepler's Laws of Planetary Motion," last edited May 31, 2017,
::2. 2017年5月31日编辑的《凯普勒行星运动法则》,

Section outline

General

反反函数

What Is an Inverse Function? ::什么是反向函数?

Inverse Functions ::反反函数

How to Find Inverse Functions ::如何查找反反函数

Example 1 ::例1

Example 2 ::例2

Example 3 ::例3

Example 4 ::例4

How to Find an Inverse Function From a Graph ::如何从图表中查找反向函数

Example 5 ::例5

How to Find an Inverse Function Algebraically ::如何查找反反函数代数

Example 6 ::例6

$ 400 : y - 1 = 1 50 ( 400 ) − 3 2 = 8 − 3 2 = 13 2 = 6 1 2 hours $ 100 : y - 1 = 1 50 ( 100 ) − 3 2 = 2 − 3 2 = 1 2 hour ::400:y-1=150(400-32=8-32=132=612小时100:y-1=150(100)-32=2-32=12小时

Example 8 ::例8

How to Find an Inverse Function With a TI-83/84 ::如何用 TI-83/84 查找反函数

Summary ::摘要

Review ::回顾

Explore More ::探索更多

Answers for Review and Explore More Problems ::回顾和探讨更多问题的答复

PLIX ::PLIX

Resources ::资源

References ::参考参考资料

What Is an Inverse Function?
::什么是反向函数?

Inverse Functions
::反反函数

How to Find Inverse Functions
::如何查找反反函数

Example 1
::例1

Example 2
::例2

Example 3
::例3

Example 4
::例4

How to Find an Inverse Function From a Graph
::如何从图表中查找反向函数

Example 5
::例5

How to Find an Inverse Function Algebraically
::如何查找反反函数代数

Example 6
::例6

Example 8
::例8

How to Find an Inverse Function With a TI-83/84
::如何用 TI-83/84 查找反函数

Summary
::摘要

Review
::回顾

Explore More

::探索更多

Answers for Review and Explore More Problems
::回顾和探讨更多问题的答复

PLIX
::PLIX

Resources
::资源

References
::参考参考资料