课程： 12.3 一般二次赤道

章节大纲

选择节常规

折叠展开
常规

全部折叠展开全部
- 选择活动新闻通告
  
  新闻通告讨论区

普通二次赤道

The path of comets can be modeled by ¹ . If the path of a comet can be modeled by the equation $\begin{aligned} 90 x^{2} + 180 y^{2} + 30 x + 60 y + 45 = 0 \end{aligned}$ , what shape does the path of the comet follow?
::1. 如果彗星的路径可以用 90x2+180y2+30x60y+45=0的方程式模拟, 彗星的路径会遵循何种形状?

In this section, we will discuss what conic sections are, and how to recognize them from equations.
::在本节中,我们将讨论什么是二次曲线,以及如何从等式中认识这些曲线。

lesson content

What Is a Conic Section?
::什么是二次曲线部分?

Conic sections are curves that can be created from the intersection of two right circular cones (also known as a double right circular cone ) and a plane.
::二次曲线系曲线,可从两个右圆锥形(又称双右圆锥形)和一平面的交汇处产生。

To form the cones, we draw a vertical axis . Then we draw a line at an angle to the axis. This line is called the generator, and the point where they intersect is called the vertex . The angle between the axis and the generator is called the vertex angle . Lastly, we rotate the generator 360 degrees around the axis to form the two cones.
::要形成锥体, 我们绘制一个垂直轴。然后在轴角上绘制一条线。这条线被称为生成器, 其交叉点被称为顶点。轴与生成器之间的角被称为顶点。最后, 我们沿着轴旋转发电机360度, 形成两个锥体。

lesson content

The surface of the cone is called the nappe . To distinguish the two nappes, we call the nappe for the top cone the upper nappe, and the nappe for the bottom cone the lower nappe .
::锥体的表面被称为环球。为了区分两个环球,我们把顶锥的环球称为上角环球,而底锥的环球称为下角环球。

Depending on how a plane intersects the nappes, we form four types of conic sections.
::取决于平面如何相互交错, 我们形成四类的二次曲线部分。

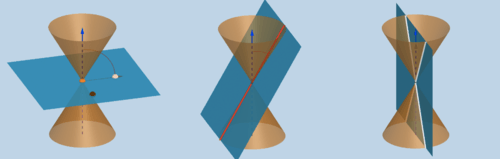
Parabola : The angle between the plane and the axis is the same as the vertex angle. We can see this in image 1 below.
::parabola: 平面与轴之间的角与顶点角相同。我们可以在下面的图像 1 中看到这一点。

Circle : The angle between the plane and the axis is a right angle. This is shown in the lower nappe of 2 below.
::圆: 平面和轴之间的角是一个右角。下角的角在下面 2 中显示。

Ellipse : The angle between the plane and the axis is greater than the vertex angle. This is shown in the upper nappe of 2 below. (Notice that a circle is a special type of ellipse.)
::椭圆 : 平面和轴之间的角大于顶点角。这在下面 2 的上角内显示。 (注意圆是一个特殊的椭圆类型。)

: The angle between the plane and the axis is less than the vertex angle. We can see this in image 3 below.
:::平面与轴之间的角小于顶点角。我们在下面的图像3中可以看到这一点。

lesson content

by MasterWuMathematics demonstrates how to find the conic sections from their intersections with two cones.
::由MasterWu数学演示如何从与两个锥形的交汇处找到锥形部分。

There are three types of degenerate conic sections—that is, shapes that satisfy the requirements for an ellipse, a parabola, and a hyperbola, but do not form those shapes.
::有三种退化的二次曲线——即满足对椭圆、抛物线和超双曲线的要求的形状,但不构成这些形状。

Point : If the plane intersects the two cones at the vertex and at an angle greater than the vertex angle, we get a point. This is a degenerate ellipse.
::点 : 如果平面在顶端交叉两个锥体, 其角大于顶端角, 我们得到一个点。这是一个退化的椭圆。

Line : If the plane intersects the two cones at the vertex and at an angle equal to the vertex angle, we get a line. This is a degenerate parabola.
::线条 : 如果平面在顶端和与顶端角相等的角度交叉两个锥体, 我们得到一条线。这是一个退化的抛物线。

Two intersecting lines : If the plane intersects the two cones at the vertex and at an angle less than the vertex angle, we get two intersecting lines. This is a degenerate hyperbola .
::两条交叉线:如果平面在顶端和低于顶端角角的两个锥体交叉,我们得到两条交叉线。这是一个退化的双曲线。

lesson content

We can also find the conic sections in two dimensions using the fact that each conic section is a locus . A locus is a set of points that satisfies a general equation, or, a fixed relationship between points. We will consider this approach in each section separately.
::我们还可以利用每个二次曲线是一诉讼地这一事实,从两个方面找到二次曲线部分。一个诉讼地是符合一般等式的一组点,或两点之间的固定关系。我们将在每一节中分别考虑这一方法。

The General Equation for Conic Sections
::二次曲线各区一般等同

We can represent all conic sections with a similar equation. We call this the general equation for conic sections.
::我们可以以相似的方程式代表所有二次曲线部分。我们称之为二次曲线部分的一般方程式。

The General Equation for Conic Sections
::二次曲线各区一般等同

\begin{aligned} A x^{2} + B x y + C y^{2} + D x + E y + F = 0, \end{aligned}

::Ax2+Bxy+Cy2+Dx+Ey+F=0;

where $\begin{aligned} A, B, C, D, E, and F \end{aligned}$ are real numbers.
::其中A,B,C,D,E,和F是真实数字。

Note: In this chapter, we will assume $\begin{aligned} B = 0 \end{aligned}$ .
::注:在本章中,我们将假定B=0。

We can determine what type of conic section we have by the relationship between $\begin{aligned} A \end{aligned}$ and $\begin{aligned} C \end{aligned}$ . (If $\begin{aligned} B \neq 0 \end{aligned}$ , then that would be part of the calculation, too.)
::我们可以根据A和C之间的关系来确定我们有哪类二次曲线部分。 (如果B0,那也将是计算的一部分。 )

How to Identify a Conic Section From the General Equation
::如何从一般等式中识别二次部分

Parabola: $\begin{aligned} A = 0 \end{aligned}$ or $\begin{aligned} C = 0 \end{aligned}$ (in general, $\begin{aligned} B^{2} - 4 A C = 0 \end{aligned}$ )
::抛物线:A=0或C=0(一般为B2-4AC=0)

Circle: $\begin{aligned} A = C \end{aligned}$ (and, in general, $\begin{aligned} B^{2} - 4 A C < 0 \end{aligned}$ )
::圆: A=C(一般为B2-4AC <0)

Ellipse: $\begin{aligned} A C > 0 \end{aligned}$ (and, in general, $\begin{aligned} A \neq C \end{aligned}$ , $\begin{aligned} B^{2} - 4 A C < 0 \end{aligned}$ )
::椭圆:AC>0(以及一般的AC、B2-4AC<0)

Hyperbola: $\begin{aligned} A C < 0 \end{aligned}$ (and, in general, $\begin{aligned} A \neq C \end{aligned}$ , $\begin{aligned} B^{2} - 4 A C > 0 \end{aligned}$ )
::Hyperbola:AC<0(以及一般AC,B2-4AC>0)

by CK-12 discusses how to identify the conic form from the equation.
::CK-12 讨论如何从方程式中识别二次形。

We can also write the equation of a conic section in what is called standard form by completing the square for the $\begin{aligned} x \end{aligned}$ -terms and the $\begin{aligned} y \end{aligned}$ -terms separately. The table below shows what the equations will look like depending on whether the axis is horizontal or vertical.
::我们还可以分别填写 x 条件和 Y 条件的正方形,在标准格式中写出二次曲线部分的方程式。下表显示这些方程式的长相,取决于轴是水平的还是垂直的。

Standard Form of Conic Sections with Center $\begin{aligned} (h, k) \end{aligned}$
::与中(h,k)

	Horizontal Axis	Vertical Axis
Circle	$\begin{aligned} (x - h)^{2} + (y - k)^{2} = r^{2} \end{aligned}$
Parabola	$\begin{aligned} (y - k)^{2} = 4 p (x - h) \end{aligned}$	$\begin{aligned} (x - h)^{2} = 4 p (y - k) \end{aligned}$
Ellipse	$\begin{aligned} \frac{(x - h)^{2}}{a^{2}} + \frac{(y - k)^{2}}{b^{2}} = 1 \end{aligned}$	$\begin{aligned} \frac{(x - h)^{2}}{b^{2}} + \frac{(y - k)^{2}}{a^{2}} = 1 \end{aligned}$
Hyperbola	$\begin{aligned} \frac{(x - h)^{2}}{a^{2}} - \frac{(y - k)^{2}}{b^{2}} = 1 \end{aligned}$	$\begin{aligned} \frac{(y - k)^{2}}{a^{2}} + \frac{(x - h)^{2}}{b^{2}} = 1 \end{aligned}$

Example 1
::例1

The path of comets can be modeled by conic sections ¹ . If the path of a comet can be modeled by the equation $\begin{aligned} 90 x^{2} + 180 y^{2} + 30 x + 60 y + 45 = 0 \end{aligned}$ , what shape does the path of the comet follow?
::彗星的路径可以通过二次曲线区块进行模型化。如果彗星的路径可以用 90x2+180y2+30x+60x+60y+45=0 的方程式进行模型化, 那么彗星的路径会遵循何种形状 ?

Solution: The path is neither a parabola nor a circle, since $\begin{aligned} A \end{aligned}$ and $\begin{aligned} C \end{aligned}$ are not equal to 0 and not equal to each other. The product of $\begin{aligned} A \end{aligned}$ and $\begin{aligned} C \end{aligned}$ is 16,200. Since it is positive, the path of the comet is an ellipse.
::解决办法:路径既不是抛物线,也不是圆圈,因为A和C不等于0,也不等于对方。A和C的产物是16,200。由于是正数,彗星的路径是椭圆。

Example 2
::例2

Determine what type of conic section $\begin{aligned} x^{2} + y^{2} - 6 x + 10 y - 6 = 0 \end{aligned}$ is, and rewrite the equation in standard form.
::确定什么类型的二次曲线区域 x2+y2 - 6x+10y - 6=0, 并以标准格式重写方程式。

Solution: W e can see that this is a circle because $\begin{aligned} A \end{aligned}$ and $\begin{aligned} C \end{aligned}$ are both equal to 1 in general form . To write the equation in standard form, s tart by rewriting the equation with the $\begin{aligned} x \end{aligned}$ -terms and $\begin{aligned} y \end{aligned}$ -terms next to each other, and moving the constant to the other side of the equation.
::解答: 我们可以看到这是一个圆, 因为 A和 C 在一般形式上都等于 1 。要以标准形式写出方程式, 首先将方程式重写为 X 条件和 y 条件, 然后将常数移动到方程式的另一面。

\begin{aligned} x^{2} + y^{2} - 6 x + 10 y - 6 = 0 \\ (x^{2} - 6 x) + (y^{2} + 10 y) = 6 \end{aligned}

::x2+y2 - 6x+10y-6=0(x2 - 6x)+(y2+10y)=6

Now, complete the square for both the $\begin{aligned} x \end{aligned}$ - and $\begin{aligned} y \end{aligned}$ -terms. Recall that we need to identify $\begin{aligned} b \end{aligned}$ for the $\begin{aligned} x \end{aligned}$ 's—that is, -6—and the $\begin{aligned} y \end{aligned}$ 's—that is, 10. To complete the square, we need to add $\begin{aligned} {(\frac{b}{2})}^{2} \end{aligned}$ to both sides of the equation (To review completing the square, please see the section on Solving Quadratic Equations by Completing the Square. )
::现在, 完成 x 和 y 术语的方块。回顾我们需要为 x 确定 b , 即 - 6 - 和 y - 即 10 。要完成方块的方块 , 我们需要在方块的双方添加 (b2) 2 (要审查完成方块 , 请参看通过完成方块解析二次方块的一节。)

\begin{aligned} (x^{2} - 6 x + 9) + (y^{2} + 10 y + 25) & = 6 + 9 + 25 \\ (x - 3)^{2} + (y + 5)^{2} & = 40 \end{aligned}

x2-6x+9)+(y2+10y+25)=6+9+25(x-3)2+(y+5)2=40

Now the equation of the circle is in standard form.
::现在圆的方程式是标准形式。

Example 3
::例3

Determine what type of conic section $\begin{aligned} 20 x^{2} - 20 y^{2} - 80 x + 240 y + 320 = 0 \end{aligned}$ is, and rewrite the equation in standard form.
::确定20x2 - 20y2 - 80x+240y+320=0的二次曲线部分的类型, 并以标准格式重写方程式。

Solution: Here, $\begin{aligned} A = 20 \end{aligned}$ and $\begin{aligned} C = - 20 \end{aligned}$ . Since their product is negative, this conic is a hyperbola.
::解答: 这里, A=20 和 C= 20。由于它们的产品为负值, 此二次曲线是一个双曲线。

As we did in the previous example, rewrite the equation, grouping the $\begin{aligned} x \end{aligned}$ -terms together and $\begin{aligned} y \end{aligned}$ -terms together, and moving the constant over to the other side. Then, factor out the GCF from each set of terms, so we can complete the square inside the parentheses.
::正如我们在前一个例子中所做的那样,重写方程,将x-条件和y-条件组合在一起,并将常数移到另一边。然后,从每套条件中将绿色气候基金计算出来,这样我们就可以完成括号内的正方形。

\begin{aligned} 20 x^{2} - 20 y^{2} - 80 x + 240 y + 320 & = 0 \\ 20 x^{2} - 80 x - 20 y^{2} + 240 y & = - 320 \\ 20 (x^{2} - 4 x) - 20 (y^{2} - 12 y) & = - 320 \end{aligned}

::20x2 - 20y2 - 20y2 - 80x+240y+320=020x2 - 80x - 20y2+240y=-32020(x2 - 4x)-20(y2 - 12y)=-320

Now complete the square for the $\begin{aligned} x \end{aligned}$ - and $\begin{aligned} y \end{aligned}$ -terms. When determining what constant will "complete the square" for each grouping, do not forget to multiply the constant by the number outside the parentheses before adding it to the other side. The standard form for a hyperbola has one side of the equation equal to 1, so we divide by -960 to get the right-hand side equal to 1.
::现在完成 x 和 y 条件的方块。当确定每个组群的常数将“ 完成方块 ” 时, 请不要忘记将常数乘以括号外的数, 然后再将其加到另一边。双倍方块的标准格式在方程式中有一面等于 1, 因此我们除以 - 960 , 以获得右方等于 1 的常数。

\begin{aligned} 20 (x^{2} - 4 x) - 20 (y^{2} - 12 y) & = - 320 \\ 20 (x^{2} - 4 x + 4) - 20 (y^{2} - 12 y + 36) & = - 320 + 80 - 720 \\ \frac{20 (x - 2)^{2}}{- 960} - \frac{20 (y - 6)^{2}}{- 960} & = \frac{- 960}{- 960} \\ - \frac{(x - 2)^{2}}{48} + \frac{(y - 6)^{2}}{48} & = 1 \\ \frac{(y - 6)^{2}}{48} - \frac{(x - 2)^{2}}{48} & = 1 \end{aligned}

::20x2-4x)-20(y2-12y)=-32020(x2-4x+4)-20(y2-12y+36)=-320+80-72020(x-2-2)2-960-20(y-6)2-960=-960-960-(x-2)2-248+(y-6)248=1(y-6)248-(x-2)248=(x-2)248=1

This is the equation of the hyperbola in standard form.
::这是标准形式的双倍波拉的方程式。

by Daniel Kopsas shows how to find the equation of a parabola in standard form.
::Daniel Kopsas展示了如何在标准格式中找到抛物线方程式。

Example 4
::例4

Identify the conic section for $\begin{aligned} 9 x^{2} + 16 y^{2} + 18 x - 135 = 0 \end{aligned}$ and rewrite each equation in standard form.
::标明 9x2+16y2+18x-135=0 的二次曲线区域,并以标准格式重写每个方程式。

Solution: Since $\begin{aligned} A \end{aligned}$ and $\begin{aligned} C \end{aligned}$ are not equal and their product is 144, this conic section is an ellipse. We need only to complete the square for the $\begin{aligned} x \end{aligned}$ -values below.
::解决方案:A和C不相等,其产品为144,所以这个二次曲线部分是一个椭圆。我们只需要完成以下 x 值的方块。

\begin{aligned} 9 x^{2} + 16 y^{2} + 18 x - 135 & = 0 \\ 9 x^{2} + 18 x + 16 y^{2} & = 135 \\ 9 (x^{2} + 2 x + 1) + 16 y^{2} & = 135 + 9 \\ 9 (x + 1)^{2} + 16 y^{2} & = 144 \\ \frac{(x + 1)^{2}}{16} + \frac{y^{2}}{9} & = 1 \end{aligned}

::9x2+166y2+18x-135=09x2+18x+166y2=1359(x2+2x+1)+16y2=135+99(x+1)2+16y2=144(x+1)216+y29=1

Example 5
::例5

Identify the conic section for $\begin{aligned} y^{2} - 3 x - 8 y + 10 = 0 \end{aligned}$ and rewrite the equation in standard form.
::识别 y2 - 3x-8y+10=0 的二次曲线区域,并以标准格式重写方程式。

Solution: There is no $\begin{aligned} x^{2} \end{aligned}$ - term , so this equation represents a parabola. We complete the square for the $\begin{aligned} y \end{aligned}$ -terms below.
::解决方案: 没有 x2- term, 因此此方程式代表一个抛物线。我们为下面的 y terms 完成方形。

\begin{aligned} y^{2} - 3 x - 8 y + 10 & = 0 \\ y^{2} - 8 y - 3 x & = - 10 \\ y^{2} - 8 y + 16 & = 3 x - 10 + 16 \\ (y - 4)^{2} & = 3 x + 6 \\ (y - 4)^{2} & = 3 (x + 2) \end{aligned}

::y2 - 3x - 8y+10=0y2 - 8y - 3x_ 3x_ 10y2 - 8y+16=3x - 10+16(y - 4)2=3x+6(y - 4)2=3(x+2)

by MATHRoberg demonstrates how to complete the square to get an equation in standard form.
::由MATHRoberg演示如何完成广场以获得标准方程式的方程式。

Example 6
::例6

Use the discriminant to determine the type of conic, and then change the equation into standard form: $\begin{aligned} x^{2} + y^{2} - 6 x + 14 y - 86 = 0 \end{aligned}$ .
::使用对角线来确定二次曲线的类型, 然后将方程式修改为标准形式 : x2+y2 - 6x+14y - 86=0 。

Solution: $\begin{aligned} A = 1, C = 1 \end{aligned}$ This is a circle.
::解答: A=1, C=1 这是圆形。

\begin{aligned} (x^{2} - 6 x + 9) + (y^{2} + 14 y + 49) & = 86 + 49 + 9 \\ (x - 3)^{2} + (y + 7)^{2} & = 144 \end{aligned}

x2-6x+9)+(y2+14y+49)=86+49+9(x-3)2+(y+7)2=144

Example 7
::例7

Use the discriminant to determine the type of conic, and then change the equation into standard form: $\begin{aligned} - 4 x^{2} + 3 y^{2} - 8 x + 24 y + 32 = 0 \end{aligned}$ .
::使用对角线来确定二次曲线的类型, 然后将方程式更改为标准形式 : - 4x2+3y2 - 8x+24y+32=0 。

Solution: $\begin{aligned} (- 4) (3) = - 12 \end{aligned}$ , this is a hyperbola. Changing it to standard form, we have:
::解答 4) (3)= 12, 这是超双波拉。更改为标准格式, 我们有 :

\begin{aligned} (- 4 x^{2} - 8 x) + (3 y^{2} + 24 y) & = - 32 \\ - 4 (x^{2} + 2 x + 1) + 3 (y^{2} + 8 y + 16) & = - 32 + 48 - 4 \\ - 4 (x + 1)^{2} + 3 (y + 4)^{2} & = 12 \\ \frac{- (x + 1)^{2}}{3} + \frac{(y + 4)^{2}}{4} & = 1 \end{aligned}

4x2-8x)+(3y2+24y)=-32(x2+2x+1)+32-4(x2+2x+1)+3(y2+8y+16)=-32(y2+48-4(x+1)2+3(y+4)2+3(y+4)2=12-(x+1)23+(y+4)24=1

Usually, we write the negative term 2nd, so the equation is $\begin{aligned} \frac{(y + 4)^{2}}{4} - \frac{(x + 1)^{2}}{3} = 1 \end{aligned}$ .
::通常,我们写负2个字,所以方程式是(y+4)24-(x+1)23=1。

Summary
::摘要

The conic sections are formed from the intersection of the surface of a double right-circular cone and a plane.
::这些二次曲线系从双右圆锥形和平面表面的交叉点形成。

There are four conic sections—parabola, circle, ellipse, and hyperbola —and three degenerate forms—point, line, and two intersecting lines.
::有四个二次曲线段——帕拉波拉、圆圈、椭圆和双曲线——以及三个退化的形态点、线和两个交叉线。

The general form of the equation of a conic section is $\begin{aligned} A x^{2} + B x y + C y^{2} + D x + E y + F = 0, \end{aligned}$ where $\begin{aligned} A, B, C, D, E, \end{aligned}$ and $\begin{aligned} F \end{aligned}$ are real numbers.
::二次曲线段方程式的一般形式是 Ax2+Bxy+Cy2+Dx+Ey+F=0,其中A、B、C、D、E和F为实际数字。

We can recognize what type of conic section the equation represents by comparing $\begin{aligned} A \end{aligned}$ and $\begin{aligned} C \end{aligned}$ . (In this chapter, we assume $\begin{aligned} B = 0 \end{aligned}$ .)
::我们可以通过比较A和C来确认方程代表的二次曲线部分的种类(在本章中,我们假定B=0)。

To find an equation of a conic section in standard form, we complete the square.
::为了在标准格式中找到二次曲线的方程式,我们完成方形。

Review
::回顾

Use the discriminant to determine the type of conic each equation represents.
::使用对比度来确定每个方程代表的二次曲线类型。

1. $\begin{aligned} 2 x^{2} + 2 y^{2} + 16 x - 8 y + 25 = 0 \end{aligned}$
::1. 2x2+2y2+16x-8y+25=0

2. $\begin{aligned} x^{2} - y^{2} - 2 x + 5 y - 12 = 0 \end{aligned}$
::2. x2 - y2 - 2x+5y - 12=0

3. $\begin{aligned} 6 x^{2} + y^{2} - 12 x + 7 y + 35 = 0 \end{aligned}$
::3. 6x2+y2-12x+7y+35=0

4. $\begin{aligned} 3 x^{2} - 15 x + 9 y - 18 = 0 \end{aligned}$
::4. 3x2-15x+9y-18=0

5. $\begin{aligned} 10 y^{2} + 6 x - 40 y + 253 = 0 \end{aligned}$
::5. 10y2+6x-40y+253=0

6. $\begin{aligned} 4 x^{2} + 4 y^{2} + 32 x + 48 y + 465 = 0 \end{aligned}$
::6. 4x2+4y2+32x+48y+465=0

Match the equation with the correct graph.
::方程式与正确的图形匹配。

lesson content

7. $\begin{aligned} x^{2} + 10 x + 4 y + 41 = 0 \end{aligned}$
::7. x2+10x+4y+41=0

8. $\begin{aligned} 4 y^{2} + x + 56 y + 188 = 0 \end{aligned}$
::8. 4y2+x+56y+188=0

9. $\begin{aligned} x^{2} + y^{2} + 10 x - 14 y + 65 = 0 \end{aligned}$
::9. x2+y2+10x-14y+65=0

10. $\begin{aligned} 25 x^{2} + y^{2} - 200 x - 10 y + 400 = 0 \end{aligned}$
::10. 25x2+y2-200x-10y+400=0

Use the discriminant to determine the type of conic. Then change the equation into standard form .
::然后将方程式改变为标准形式。

11. $\begin{aligned} x^{2} - 12 x + 6 y + 66 = 0 \end{aligned}$
::11. x2 - 12x+6y+66=0

12. $\begin{aligned} x^{2} + y^{2} + 2 x + 2 y - 2 = 0 \end{aligned}$
::12. x2+y2+2x+2y-2=0

13. $\begin{aligned} x^{2} - y^{2} - 10 x - 10 y - 10 = 0 \end{aligned}$
::13. x2-y2-10x-10y-10=0

14. $\begin{aligned} y^{2} - 10 x + 8 y + 46 = 0 \end{aligned}$
::14. y2 - 10x+8y+46=0

15. $\begin{aligned} 3 x^{2} + 3 y^{2} - 6 x + 9 y - 14 = 0 \end{aligned}$
::15. 3x2+3y2-6x+9y-14=0

16. $\begin{aligned} 6 x^{2} + 12 x - y + 15 = 0 \end{aligned}$
::16. 6x2+12x-y+15=0

17. $\begin{aligned} x^{2} + 2 y^{2} + 4 x + 2 y - 27 = 0 \end{aligned}$
::17. x2+2y2+4x+2y-27=0

18. $\begin{aligned} x^{2} - y^{2} + 3 x - 2 y - 43 = 0 \end{aligned}$
::18. x2-y2+3x-2y-43=0

19. $\begin{aligned} y^{2} - 8 x - 6 y + 49 = 0 \end{aligned}$
::19. y2-8x-6y+49=0

20. $\begin{aligned} - 64 x^{2} + 225 y^{2} - 256 x - 3150 y - 3631 = 0 \end{aligned}$
::20.64x2+225y2-256x-3150y-3631=0

Answers for Review Problems
::回顾问题的答复

Please see the Appendix.
::请参看附录。

References
::参考参考资料

1. "HubbleSite-Reference Desk FAQs,"
::1. "二重物名参考服务台 "FAQs"

章节大纲

常规

普通二次赤道

What Is a Conic Section? ::什么是二次曲线部分?

The General Equation for Conic Sections ::二次曲线各区一般等同

The General Equation for Conic Sections ::二次曲线各区一般等同

How to Identify a Conic Section From the General Equation ::如何从一般等式中识别二次部分

Example 1 ::例1

Example 2 ::例2

Example 3 ::例3

Example 4 ::例4

Example 5 ::例5

Example 6 ::例6

Example 7 ::例7

Summary ::摘要

Review ::回顾

Answers for Review Problems ::回顾问题的答复

References ::参考参考资料

What Is a Conic Section?
::什么是二次曲线部分?

The General Equation for Conic Sections
::二次曲线各区一般等同

The General Equation for Conic Sections
::二次曲线各区一般等同

How to Identify a Conic Section From the General Equation
::如何从一般等式中识别二次部分

Example 1
::例1

Example 2
::例2

Example 3
::例3

Example 4
::例4

Example 5
::例5

Example 6
::例6

Example 7
::例7

Summary
::摘要

Review
::回顾

Answers for Review Problems
::回顾问题的答复

References
::参考参考资料