Course: 1.12 坐标几何 | The Way To Learn

The Way To Learn

Section outline

Select section General

Collapse Expand
General

Collapse all Expand all
- Select activity 新闻通告
  
  新闻通告 Forum
Select section 坐标几何

Collapse Expand
坐标几何
Introduction
::导言

Much of algebraic representation occurs within the coordinate (or Cartesian) plane. This lesson will review how to represent points, lines, and parallel and perpendicular lines graphically.
::许多代数表示式出现在坐标(或笛卡尔)平面内,该课程将用图形方式审查如何代表点、线条、平行线和垂直线。

The Coordinate Plane
::协调计划

The coordinate plane can be thought of as two number lines that meet at right angles. The horizontal line is called the $\begin{aligned} x \end{aligned}$ -axis and the vertical line is called the $\begin{aligned} y \end{aligned}$ -axis. Together the lines are called the axes , and the point at which they cross is called the origin . The axes split the coordinate plane into four quadrants , which are numbered sequentially (I, II, III, IV) moving counterclockwise from the upper right.
::坐标平面可被视为在右角度相交的两条数字线。水平线称为 X 轴, 垂直线称为 Y 轴。横线加起来称为轴, 其交叉点则称为原点。轴将坐标平面分割成四个四方位, 从右上方按顺序编号( 一、二、三、四) , 从右上方逆时针移动。

Identify Coordinates of Points
::确定各点的坐标

When given a point on a coordinate plane, you can easily determine its coordinates . The coordinates of a point are two numbers , and written together they are called an ordered pair . The numbers describe how far along the $\begin{aligned} x \end{aligned}$ -axis and $\begin{aligned} y \end{aligned}$ -axis the point is. The ordered pair is written in " data-term="Parentheses" role="term" tabindex="0"> parentheses , with the $\begin{aligned} x \end{aligned}$ -coordinate (also called the abscissa ) 1st and the $\begin{aligned} y \end{aligned}$ -coordinate ( also known as the ordinate ) 2nd.
::当在坐标平面上给定一个点时,您可以很容易地确定其坐标。一个点的坐标是两个数字,它们一起写成,被称为一个有顺序的对。数字说明在x轴和y轴之间的距离。定的对以括号写,有x坐标(也称为 abscissa) 1 和 y坐标(也称为坐标) 2 。

$\begin{aligned} \begin{aligned} (1, 7) & An ordered pair with an x -value of 1 and a y -value of 7 \\ (0, 5) & An ordered pair with an x -value of 0 and a y -value of 5 \\ (- 2.5, 4) & An ordered pair with an x -value of -2.5 and a y -value of 4 \\ (- 107.2, - 0.005) & An ordered pair with an x -value of -107.2 and a y -value of - 0.005 \end{aligned} \end{aligned}$
:1,7) 定购对,X值为1,Y值为7(0,0,5) 定购对,X值为0,Y值为5(2.5,4) 定购对,X值为-2.5,Y值为4(107.2,-0.005) 定购对,x值为-107.2,Y值为-0.005)

Identifying coordinates is just like reading points on a number line, except that the points do not actually lie on the number line!
::识别坐标与数字行的读点相同,但数字线上的点实际上并不在数字线上!

Plot Points in a Coordinate Plane
::坐标平面中的绘图点

Plotting points is simple, once you understand how to read coordinates and the scale on a graph. As a note on scale, in the next two examples pay close attention to the labels on the axes.
::绘图点很简单, 一旦您了解如何在图表中读取坐标和比例尺。作为比例说明, 在接下来的两个示例中, 密切关注轴上的标签。

Watch this video for help with the examples below:
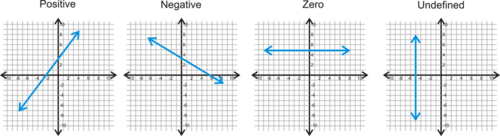
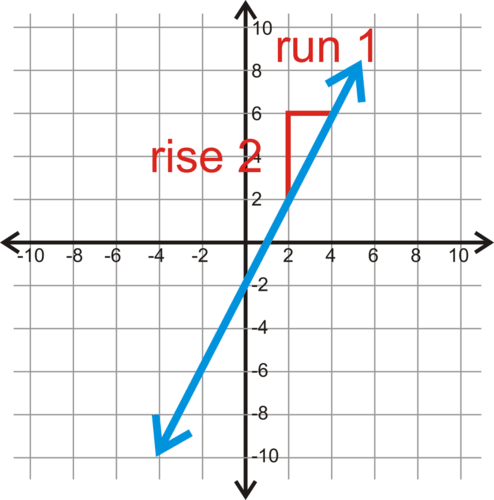
::观看这段影片,

Slope
::斜斜度

The following video provides an overview on the concept of the of a line. It defines slope, gives the formula , and works through examples:
::以下视频概述了一条线的概念。它界定斜坡,给出公式,并通过实例发挥作用:

Slope is the change in vertical direction over the change in horizontal direction. It is defined as the $\begin{aligned} \frac{rise}{run} \end{aligned}$ .
::斜坡是垂直方向相对于水平方向变化的变化。它被定义为上升。

Slope of Line between Two Points
::两点间线的曲线

The slope of the line passing through two points $\begin{aligned} (x_{1}, y_{1}) \end{aligned}$ and $\begin{aligned} (x_{2}, y_{2}) \end{aligned}$ is $\begin{aligned} m = \frac{(y_{2} - y_{1})}{(x_{2} - x_{1})} \end{aligned}$ .

Different Types of Slope :
::不同的斜坡类型 :

Watch this video for help with the examples below:
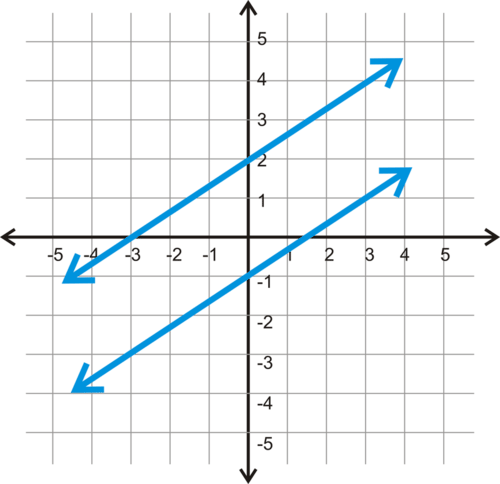
::观看这段影片,

Parallel Lines in the Coordinate Plane
::坐标平面的平行线

Parallel lines are two lines that never intersect. In the coordinate plane, that would look like this:
::平行线是两条从不交叉的线条。在坐标平面上,这看起来像:

If we take a closer look at these two lines, we see that the slopes are both $\begin{aligned} \frac{2}{3} \end{aligned}$ .
::如果我们仔细看一看这两条线,我们可以看到,斜坡是23。

This can be generalized to any pair of parallel lines. Parallel lines always have the same slope and different $\begin{aligned} y - \end{aligned}$ intercepts .
::平行线总是有相同的斜坡和不同的y-inter概念。

What if you were given two parallel lines in the coordinate plane? What could you say about their slopes?
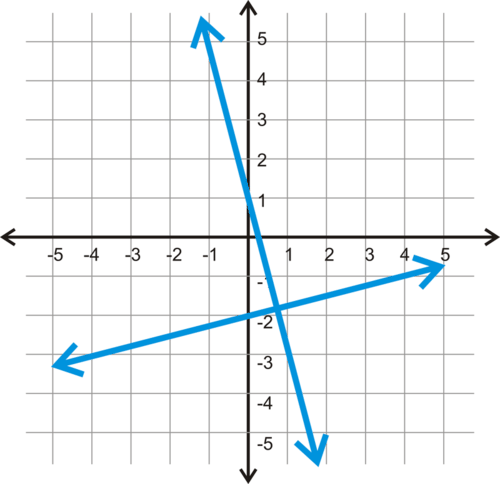
::如果在座标飞机上给你两条平行线呢?

Perpendicular Lines in the Coordinate Plane
::坐标平面上的直直线

Perpendicular lines are two lines that intersect at a $\begin{aligned} 90^{\circ} \end{aligned}$ or right angle. In the coordinate plane, that would look like this:
::垂直线是两条线,在90°C或右角交叉。在坐标平面上,这看起来像:

If we take a closer look at these two lines, we see the slope of one is -4 and the other is $\begin{aligned} \frac{1}{4} \end{aligned}$ .
::如果我们仔细看一看这两条线,我们看到一的斜坡是 -4,另一的斜坡是14。

This can be generalized to any pair of perpendicular lines in the coordinate plane. The slopes of perpendicular lines are negative reciprocals of each other.
::这可以推广到坐标平面上任何一条垂直线,垂直线的斜坡是相互负对等的。

This video explores the relationship between the slopes of perpendicular lines:
::这段影片探索垂直线斜坡之间的关系:

Examples
::实例

Example 1
::例1

Find the coordinates of the point labeled $\begin{aligned} P \end{aligned}$ in the diagram above.
::在上面的图表中找到标有 P 点的坐标。

Solution:
::解决方案 :

Imagine you are standing at the origin (the point where the $\begin{aligned} x \end{aligned}$ -axis meets the $\begin{aligned} y \end{aligned}$ -axis). In order to move to a position where $\begin{aligned} P \end{aligned}$ is directly above you, you would move 3 units to the right. (We say this is in the positive $\begin{aligned} x \end{aligned}$ direction.)
::想象一下您站在原点( X 轴与 Y 轴相交的点) 。为了移动到 P 直接在你上方的位置, 您会移动到右边的 3 个单位。 (我们说这是正 x 方向。 )

The $\begin{aligned} x \end{aligned}$ -coordinate of $\begin{aligned} P \end{aligned}$ is +3.
::P的x坐标为+3。

Now, if you were standing at the 3 marker on the $\begin{aligned} x \end{aligned}$ -axis, point $\begin{aligned} P \end{aligned}$ would be 7 units above you. (Above the axis means it is in the positive $\begin{aligned} y \end{aligned}$ direction.)
::现在,如果你站在X轴上方的3个标记处,P点在你上面7个单位。 (轴是正向y方向。 )

The $\begin{aligned} y \end{aligned}$ -coordinate of $\begin{aligned} P \end{aligned}$ is +7.
::P的 Y 坐标是+ 7 。

The coordinates of point $\begin{aligned} P \end{aligned}$ are (3, 7).
::P点的坐标是(3,7)

Example 2
::例2

Find the coordinates of the points labeled $\begin{aligned} Q \end{aligned}$ and $\begin{aligned} R \end{aligned}$ in the diagram above .
::在上述图表中查找标有Q和R的点的坐标。

Solution:
::解决方案 :

In order to get to $\begin{aligned} Q \end{aligned}$ , we move 3 units to the right, in the positive $\begin{aligned} x \end{aligned}$ direction, then 2 units down, in the negative $\begin{aligned} y \end{aligned}$ direction. The $\begin{aligned} x \end{aligned}$ -coordinate of $\begin{aligned} Q \end{aligned}$ is +3, and the $\begin{aligned} y \end{aligned}$ -coordinate of $\begin{aligned} Q \end{aligned}$ is −2.
::为了到达Q,我们将3个单位向右移动,向正x方向移动,然后向下移动2个单位,向负y方向移动。Q的x坐标是+3,而Q的Y坐标是-2。

The coordinates of $\begin{aligned} R \end{aligned}$ are found in a similar way. The $\begin{aligned} x \end{aligned}$ -coordinate is +5 (meaning 5 units in the positive $\begin{aligned} x \end{aligned}$ direction), and the $\begin{aligned} y \end{aligned}$ -coordinate is again −2.
::R 的坐标也以类似的方式找到。 x 坐标是+ 5 (表示正向 x 方向 5 个单位),Y 坐标是 -2 。

The coordinates of $\begin{aligned} Q \end{aligned}$ are (3, −2). The coordinates of $\begin{aligned} R \end{aligned}$ are (5, −2).
::Q座标为(3,-2),R座标为(5,-2)。

Example 3
::例3

Triangle $\begin{aligned} A B C \end{aligned}$ is shown in the diagram below. Find the coordinates of the vertices $\begin{aligned} A, B \end{aligned}$ , and $\begin{aligned} C \end{aligned}$ .
::三角 ABC 显示在下图中。请查找 A、B 和 C 顶点的坐标。

Solution:
::解决方案 :

Point $\begin{aligned} A \end{aligned}$ : $\begin{aligned} A (- 2, 5) \end{aligned}$
::A点:A(-2,5)

$\begin{aligned} x -coordinate = - 2 \end{aligned}$
::x坐标坐标=-2

$\begin{aligned} y -coordinate = + 5 \end{aligned}$
::y- 坐标% 5

Point $\begin{aligned} B \end{aligned}$ : $\begin{aligned} B (3, - 3) \end{aligned}$
::B点:B(3,3,3)

$\begin{aligned} x -coordinate = + 3 \end{aligned}$
::x 坐标% 3

$\begin{aligned} y -coordinate = - 3 \end{aligned}$
::Y 坐标=-3

Point $\begin{aligned} C \end{aligned}$ : $\begin{aligned} C (- 4, - 1) \end{aligned}$
::C点:C(4-4-1)

$\begin{aligned} x -coordinate = - 4 \end{aligned}$
::x坐标坐标=-4

$\begin{aligned} y -coordinate = - 1 \end{aligned}$
::Y- 坐标=-1

Example 4
::例4

Plot the following points on the coordinate plane:
::在坐标平面上绘制下列点:

$\begin{aligned} A (2, 7) B (- 4, 6) D (- 3, - 3) E (0, 2) F (7, - 5) \end{aligned}$
::A(2,7)B(4,6)D(3,3)E(0,2)F(7,5)

Solutions:
::解决办法:

Point $\begin{aligned} A (2, 7) \end{aligned}$ is 2 units right, 7 units up. It is in Quadrant I.
::A点( 2, 7) 是 2 个单位右侧, 向上 7 个单位。在 Quadrant I 中。

Point $\begin{aligned} B (- 4, 6) \end{aligned}$ is 4 units left, 6 units up. It is in Quadrant II.
::B点( 4, 6) 是剩下4个单元, 向上 6个单元, 在 Quadrant II 中。

Point $\begin{aligned} D (- 3, - 3) \end{aligned}$ is 3 units left, 3 units down. It is in Quadrant III.
::D( 3 - 3) 点是左3个单位, 向下3个单位, 在 Quadrant III 中。

Point $\begin{aligned} E (0, 2) \end{aligned}$ is 2 units up from the origin. It is right on the $\begin{aligned} y \end{aligned}$ -axis, between Quadrants I and II.
::点E( 0. 2) 是从源起向上移动的 2 个单位。它位于 y 轴上, 介于夸德兰特 II 和 II 之间。

Point $\begin{aligned} F (7, - 5) \end{aligned}$ is 7 units right, 5 units down. It is in Quadrant IV.
::F(7,5)点是右7个单位,向下5个单位,在Quadrant IV。

Example 5
::例5

a) What is the slope of the line through (2, 2) and (4, 6)?
:a) 线的坡度是多少(2、2和4、6)?

Solution:
::解决方案 :

Use the slope formula to determine the slope. Use (2, 2) as $\begin{aligned} (x_{1}, y_{1}) \end{aligned}$ and (4, 6) as $\begin{aligned} (x_{2}, y_{2}) \end{aligned}$ .
::使用斜坡公式确定斜坡。使用 2( 2, 2) 作为 (x1, y1) , 4, 6) 作为 (x2, y2) 。

$\begin{aligned} m = \frac{y_{2} - y_{1}}{x_{2} - x_{1}} = \frac{6 - 2}{4 - 2} = \frac{4}{2} = 2 \end{aligned}$

::my2-y1x2-x1=6-24-2=42=2

Therefore , the slope of this line is 2. This slope is positive.
::因此,这条线的斜坡是2。这个斜坡是正的。

b) Find the slope between (-8, 3) and (2, -2).
:b) 在(8,3)和(2,2)之间找到斜坡。

Solution:
::解决方案 :

$\begin{aligned} m = \frac{- 2 - 3}{2 - (- 8)} = \frac{- 5}{10} = - \frac{1}{2} \end{aligned}$

::m2 - 32 - (-8) 510 - 12

This is a negative slope .
::这是一个负斜坡。

c) Find the slope between (-5, -1) and (3, -1).
:c) 在(5-1)和(3-1)之间找到斜坡。

Solution:
::解决方案 :

$\begin{aligned} m = \frac{- 1 - (- 1)}{3 - (- 5)} = \frac{0}{8} = 0 \end{aligned}$

::m1 - (- 1) 3 - (-5) = 08=0

Therefore, the slope of this line is 0, which means it is a horizontal line. Horizontal lines always pass through the $\begin{aligned} y - \end{aligned}$ axis. Notice that the $\begin{aligned} y - \end{aligned}$ coordinate for both points is -1. In fact, the $\begin{aligned} y - \end{aligned}$ coordinate for any point on this line is -1. This means the horizontal line must cross $\begin{aligned} y = - 1 \end{aligned}$ .
::因此,这条线的斜坡是 0, 意思是它是一个水平线。水平线总是通过 y - 轴线。请注意, 两个点的 y - 坐标是 - 1 。事实上, 该线上任何点的 y - 坐标是 - 1 。这意味着水平线必须横过 y * 1 。

d) Find the slope of the line through (3, 2) and (3, 6).
:d) 找到横穿线的斜坡(3,2)和(3,6)。

Solution:
::解决方案 :

$\begin{aligned} m = \frac{6 - 2}{3 - 3} = \frac{4}{0} = u n d e f i n e d \end{aligned}$

::m=6 - 23 - 3=40=未定义

Therefore, the slope of this line is undefined , which means it is a vertical line. Vertical lines always pass through the $\begin{aligned} x - \end{aligned}$ axis. Notice that the $\begin{aligned} x - \end{aligned}$ coordinate for both points is 3. In fact, the $\begin{aligned} x - \end{aligned}$ coordinate for any point on this line is 3. This means the vertical line must cross $\begin{aligned} x = 3 \end{aligned}$ .
::因此,这条线的斜坡是未定义的, 这意味着它是一条垂直线。垂直线总是通过 x- 轴线。注意两个点的 x- 坐标是 3 。事实上, 这条线上任何点的 x- 坐标是 3 。这意味着垂直线必须跨 x= 3 。

Example 6
::例6

a) Find the slope of the line that is perpendicular to this line: $\begin{aligned} y = - \frac{2}{3} x - 5 \end{aligned}$ .
:a) 找到与该线垂直的线的斜坡:y23x-5。

Solution:
::解决方案 :

$\begin{aligned} m = - \frac{2}{3} \end{aligned}$ , take the reciprocal and change the sign, $\begin{aligned} m_{⊥} = \frac{3}{2} \end{aligned}$ (⊥ is the notation for perpendicular) .
::má23, 拿对等的, 并更改符号, m32 (是垂直的标记) 。

b) Find the slope of the line that is perpendicular to this line: $\begin{aligned} y = x + 2 \end{aligned}$ .
:b) 查找与该线垂直的线的斜坡:y=x+2。

Solution:
::解决方案 :

Because there is no number in front of $\begin{aligned} x \end{aligned}$ , the slope is 1. The reciprocal of 1 is 1, so the only thing to do is make it negative, $\begin{aligned} m_{⊥} = - 1 \end{aligned}$ .
::因为x前面没有数字, 斜坡是 1 。 1 的对等值是 1, 所以唯一要做的就是让它负, m1 。

Example 7
::例7

Find the equation of the line that is perpendicular to $\begin{aligned} y = - \frac{1}{3} x + 4 \end{aligned}$ and passes through (9, -5).
::查找与 y13x+4 垂直的直线的方程,然后通过 (9,5) 。

Solution:
::解决方案 :

First, the slope is the opposite reciprocal of $\begin{aligned} - \frac{1}{3} \end{aligned}$ . So, $\begin{aligned} m = 3 \end{aligned}$ .
::首先,斜坡是-13的对等。所以,m=3。

The equation of a line can be written using slope-intercept form , $\begin{aligned} y = m x + b \end{aligned}$ .
::线条的方程式可以用 y=mx+b 的斜体界面写出。

Plug in 9 for $\begin{aligned} x \end{aligned}$ and -5 for $\begin{aligned} y \end{aligned}$ to solve for the new $\begin{aligned} y - \end{aligned}$ intercept $\begin{aligned} (b) \end{aligned}$ :
::x 和 - 5 y 的插件在 9 中, 用于 y - interfict (b) 的 y - interview (b) 解答 :

$\begin{aligned} - 5 & = 3 (9) + b \\ - 5 & = 27 + b \\ - 32 & = b \end{aligned}$

::- 5=3(9)+b-5=27+b-32=b

Therefore, the equation of the perpendicular line is $\begin{aligned} y = 3 x - 32 \end{aligned}$ .
::因此,垂直直线的方程式是y=3x-32。

Note that you can use the same process, but keep the slope identical if solving for the equation of the line that is parallel.
::请注意,您可以使用相同的进程,但如果解决平行线的方程式,则保持斜度相同。

Example 8
::例8

Graph $\begin{aligned} 3 x - 4 y = 8 \end{aligned}$ and $\begin{aligned} 4 x + 3 y = 15 \end{aligned}$ . Determine if they are perpendicular.
::图3 - 4y=8和4x+3y=15。确定它们是垂直的。

Solution:
::解决方案 :

First we have to change each equation into slope-intercept form. In other words, we need to solve each equation for $\begin{aligned} y \end{aligned}$ :
::首先,我们必须将每个方程式改变为斜坡界面形式。换句话说, 我们需要为 y 解析每个方程式 :

$\begin{aligned} 3 x - 4 y & = 8 & 4 x + 3 y = 15 \\ - 4 y & = - 3 x + 8 & 3 y = - 4 x + 15 \\ y & = \frac{3}{4} x - 2 & y = - \frac{4}{3} x + 5 \end{aligned}$

::3x-4y=84x+3y=15-4y3x+83y4x+15y=34x-2y43x+5

Now that the lines are in slope-intercept form (also called $\begin{aligned} y - \end{aligned}$ intercept form), we can tell they are perpendicular because their slopes are opposite reciprocals.
::现在线以斜坡界面的形式(也称为 y - interphysict form)出现, 我们可以看出来它们是垂直的, 因为它们的斜坡是相反的对等的。

Example 9
::例9

Find the slope of the interval between the two given points:
::查找两个给定点间距的斜坡 :

a) (3, -4) and (3, 7)
:a) (3,4)和(3,7)

Solution:
::解决方案 :

These two points create a vertical line, so the slope is undefined.
::这两个点形成一条垂直线,所以斜坡是未定义的。

b) (6, 1) and (4, 2)
:b) (6,1)和(4,2)

Solution:
::解决方案 :

The slope is $\begin{aligned} \frac{(2 - 1)}{(4 - 6)} = - \frac{1}{2} \end{aligned}$ .
::斜坡为(2-1)(4-6)12。

c) (5, 7) and (11, 7)
:c) (5,7)和(11,7)

Solution:
::解决方案 :

These two points create a horizontal line, so the slope is zero.
::这两个点形成水平线,所以斜坡为零。

Review
::回顾

Identify the coordinates of each point, $\begin{aligned} A - F \end{aligned}$ , on the graph below.

::在下图中标明每个点的坐标A-F。

Draw a line on the above graph connecting point $\begin{aligned} B \end{aligned}$ with the origin. Where does that line intersect the line connecting points $\begin{aligned} C \end{aligned}$ and $\begin{aligned} D \end{aligned}$ ?
::绘制上图中连接点B和来源的线条。该线条在哪里交叉连接点C和D的线条?

Identify which quadrant each point lies in:
::确定每个点的象限值 :

(4, 2)

(-3, 5.5)

(4, -4)

(-3, -5)

Find the slope between the two given points:
::查找两个给定点之间的斜坡 :

(-9, 5) and (-6, 2)
:9,5)和(6,2)

(-6, 0) and (-1, -10)
:-6,0)和(-1,-10)

(1, -2) and (3, 6)
:1,2)和(3,6)

(-4, 5) and (-4, -3)
:-4、5和4)和(-4、3)

(4, 1) and (7, 1)
:第4、第1、第4、第1和第7、第1段)

(13, 12) and (-23, 14)
:13、12)和(23、14)

(-4, 2) and (-16, 12)
:4-4,2)和(16,12)

Determine if each pair of lines are parallel, perpendicular, or neither. Then graph each pair on the same set of axes:
::确定每一条线是否平行, 垂直, 或两者都不是。然后在同一组轴上绘制每对图 :

$\begin{aligned} y = 4 x - 2 \end{aligned}$ and $\begin{aligned} y = 4 x + 5 \end{aligned}$
::y=4x-2和y=4x+5 y=4x-2和y=4x+5

$\begin{aligned} y = - x + 5 \end{aligned}$ and $\begin{aligned} y = x + 1 \end{aligned}$
::yx+5和y=x+1 yx+5和y=x+1

$\begin{aligned} 5 x + 2 y = - 4 \end{aligned}$ and $\begin{aligned} 5 x + 2 y = 8 \end{aligned}$
::5x+2y4和5x+2y=8

$\begin{aligned} y = - 2 x + 3 \end{aligned}$ and $\begin{aligned} y = \frac{1}{2} x + 3 \end{aligned}$
::y2x+3和y=12x+3

$\begin{aligned} y = - 3 x + 1 \end{aligned}$ and $\begin{aligned} y = 3 x - 1 \end{aligned}$
::y3x+1和y=3x-1

Determine the equation of the line that is parallel to the given line, through the given point:
::通过给定点确定与给定线平行的线条的方程 :

$\begin{aligned} y = - 5 x + 1; (- 2, 3) \end{aligned}$
::y5x+1;(-2,3)

$\begin{aligned} y = \frac{2}{3} x - 2; (9, 1) \end{aligned}$
::y=23x-2; (9,1)

$\begin{aligned} x - 4 y = 12; (- 16, - 2) \end{aligned}$
::x-4y=12; (- 16-2)

Determine the equation of the line that is perpendicular to the given line, through the given point:
::通过给定点确定与给定线垂直的线条的方程:

$\begin{aligned} y = x - 1; (- 6, 2) \end{aligned}$
::y=x-1; (- 6, 2)

$\begin{aligned} y = 3 x + 4; (9, - 7) \end{aligned}$
::y=3x+4; (9,-7)

$\begin{aligned} 5 x - 2 y = 6; (5, 5) \end{aligned}$
::5x-2yy=6; (5,5)

$\begin{aligned} y = 4; (- 1, 3) \end{aligned}$
::y=4; (-1) (-1)

Review (Answers)
::回顾(答复)

Please see the Appendix.
::请参看附录。

版权所有 © 2024 由瓜瓜科技thewaytolearn.cn设计。保留所有权利。