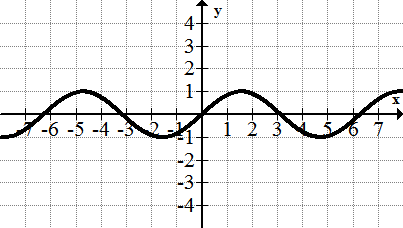2.2 域和范围

章节大纲

• 选择节常规

  折叠 展开

  常规

  全部折叠 展开全部

  • 选择活动新闻通告

    

    新闻通告 讨论区
• 选择节域和范围

  折叠 展开

  域和范围

  播放段落

  Introduction
  ::导言

  播放段落

  Mathematical functions represent a rule of correspondence and are used to produce information. For example, the height of a rounded bridge over a brook is expressed by  $\begin{array}{r}h(x)=\sqrt{12x-x^2},\end{array}$  where $\begin{array}{r}x\end{array}$  is the horizontal distance traveled from one shore to the other. Because the brook is 12 feet wide, this function is defined with the boundary   $\begin{array}{r}0\le x\le 12\end{array}$ . The domain (which we will define in this lesson ) of the function is this set of values for $\begin{array}{r}x\end{array}$ . Similarly, the bridge is 6 feet high so the values for the height are limited. The range (which we will also define in this lesson) of the function is $\begin{array}{r}0\le h(x)\le 6\end{array}$ .  
  ::数学函数代表通信规则, 用于生成信息 。 例如, 圆形桥的高度以 h( x) = 12x- x2 表示, 其中 x 是从一个海岸到另一个海岸的水平距离 。 由于 brook 是 12 英尺宽, 此函数以 0. x= 12 的边界来定义 。 此函数的域( 我们将在此课中定义) 是 x 的这组值 。 同样, 桥的高度是 6 英尺高, 因此高度的值是有限的 。 此函数的范围( 我们将在此课中定义) 是 0°h ( x) 6 。

  播放段落

  The following interactive PLIX example also illustrates t hese concepts with the s cope of sunrise to sunset:  .
  ::以下互动的PLIX实例也说明了日出到日落的范围:

  播放段落

  Domain
  ::域域域域

  播放段落

  The domain of a function is the set of all $\begin{array}{r}x\end{array}$ -values for which a function is defined. In the above exploration of the path of the sun, the domain is the set of time values past dawn , and range from 0 to 12 hours.  For the function $\begin{array}{r}y=3x\end{array}$ , the domain is the set of all real numbers, often written as $\begin{array}{r}\mathbb{R}\end{array}$ . The domain of the function $\begin{array}{r}y=\sqrt{x}\end{array}$ is the set of all real numbers  greater than or equal to 0, because the square root of a negative number is not defined in the real number system. 
  ::函数的域是定义函数的所有 x 值的集合。 在上述对太阳路径的探索中, 域是过去黎明的时间值的集合, 范围为 0 到 12 小时。 对于函数 y= 3x, 域是所有真实数字的集合, 通常写成为 R 。 函数 y=x 的域是所有实际数字大于或等于 0 的集合, 因为负数的平根在实际数字系统中没有定义 。

  播放段落

  The variable $\begin{array}{r}x\end{array}$  is often referred to as the independent variable, while the variable $\begin{array}{r}y\end{array}$  is referred to as the dependent variable, because the $\begin{array}{r}y\end{array}$ -values of a function depend on the corresponding  $\begin{array}{r}x\end{array}$ -values. 
  ::变量 x 通常称为独立变量,而变量 y 则称为依赖变量,因为函数的 Y 值取决于相应的 x 值。

  播放段落

  Range
  ::范围范围范围

  播放段落

  The range of a function is defined as the set of all $\begin{array}{r}y\end{array}$ -values for which a function is defined. Just as with the domain, the range can be described. Consider for example the function $\begin{array}{r}y=x^2\end{array}$ . The domain of this function is all real numbers  $\begin{array}{r}\mathbb{R}\end{array}$ , but what about the range?
  ::函数的范围被定义为定义函数的所有 Y 值的一组。与域一样,可以描述范围。例如,函数 y=x2 。此函数的域是所有真实数字 R,但范围呢?

  播放段落

  The range of this function is the set of all real numbers greater than or equal to 0, since every  $\begin{array}{r}y\end{array}$ -value is the square of an $\begin{array}{r}x\end{array}$ -value. 
  ::此函数的范围是所有大于或等于 0 的实际数字的一组,因为每个 Y 值是 x 值的正方形。

   

  播放段落

  Interval Notation
  ::间间点

  播放段落

  are often described in interval notation. Interval notation is used to describe set s of numbers, such as when describing domain and range. Intervals are either open or closed or both. Open intervals use " data-term="Parentheses" role="term" tabindex="0"> parentheses and refer to intervals that do not include the endpoints. Closed intervals use square or box brackets [ ] and refer to intervals that do include the endpoints. Braces or curly brackets { } are used when the domain or range consists of discrete numbers and not an interval of values. 
  ::通常用间距标记来描述数组,例如在描述域和范围时,则使用中间符号来描述数组。中间符号是开放的或封闭的,或者两者兼而有之。开放间隔使用括号 , 指不包括终点的间隔。 封闭间隔使用方格或框括号[ ], 指包括终点的间隔。 当域或范围由离散数字而不是数值间隔组成时, 使用括号或卷括号{} 。

  播放段落

  If the domain or range of a function is all numbers, the notation includes negative and positive infinity  $\begin{array}{r}(-\mathrm{\infty },\mathrm{\infty })\end{array}$ . If the domain is all positive numbers plus  0, the domain would be written as  $\begin{array}{r}\left[0,\mathrm{\infty }\right)\end{array}$ .  If the range  of a function is e very number between 5 and 6 but not including 5 or 6, the notation would be (5 , 6).
  ::如果函数的域或范围是所有数字,则标记包括负和正的无限性(,)。如果域是正数加0,则域将写成[0,]。如果函数的范围为5至6之间的每个数,但不包括5或6,则标记为(5,6)。

  播放段落

  In addition ,  $\begin{array}{r}\in \end{array}$  is a symbol that means "is an element of," and  $\begin{array}{r}\cup \end{array}$  is a symbol that means " union ." This latter symbol is used to connect two groups and is associated with the logical term OR. 
  ::后一符号用于连接两个组, 并且与 OR 逻辑术语相关。

  播放段落

  Examples
  ::实例

  播放段落

  Example 1
  ::例1

  播放段落

  Explain the domain and range of the square root function  $\begin{array}{r}y=\sqrt{x}\end{array}$ . 
  ::解释正方根函数 y=x 的域和范围 。

  播放段落

  Solution:
  ::解决方案 :

  播放段落

  Domain:  $\begin{array}{r}x\ge 0\end{array}$
  ::域名: x% 0

  播放段落

  Range:   $\begin{array}{r}y\ge 0\end{array}$
  ::范围: y=0

  播放段落

  The square root of a negative number is not a real number, so the domain is restricted. The domain and range can be observed with the graph of a function , because the curve is only defined where   $\begin{array}{r}x\end{array}$  and $\begin{array}{r}y\end{array}$  are nonnegative. 
  ::负数的平方根不是一个实际数字, 因此域是受限制的。 域和范围可以用函数的图形来观察, 因为曲线只在 x 和 y 无负值的地方定义 。

  

  播放段落

  Example 2
  ::例2

  播放段落

  Explain the domain and range of the  reciprocal function  $\begin{array}{r}y=\frac{1}{x}.\end{array}$
  ::解释对等函数 y=1x 的域和范围 。

  播放段落

  Solution:
  ::解决方案 :

  播放段落

  Domain:  $\begin{array}{r}x\ne 0\end{array}$
  ::域名: x0

  播放段落

  Range:  $\begin{array}{r}y\ne 0\end{array}$
  ::范围: y0

  播放段落

  The reciprocal function is restricted because division by 0 is not defined. This restriction can be observed in the graph of the function by the fact that   $\begin{array}{r}y\end{array}$  approaches both  $\begin{array}{r}-\mathrm{\infty }\end{array}$  and $\begin{array}{r}\mathrm{\infty }\end{array}$ ,  as   $\begin{array}{r}x\end{array}$  approaches 0 from both the left and the right. Also,  $\begin{array}{r}y\end{array}$   approaches 0 as $\begin{array}{r}x\end{array}$  approaches  $\begin{array}{r}-\mathrm{\infty }\end{array}$  and  $\begin{array}{r}\mathrm{\infty }.\end{array}$
  ::互惠函数受到限制, 原因是未定义除以 0 。 在函数图中可以观察到这一限制,因为 y 既接近 也接近 ; y 接近 0 y 接近 0 x

   

  播放段落

  Example 3
  ::例3

  播放段落

  Identify the domain and range for the following function:
  ::确定下列函数的域和范围:

  

  播放段落

  Solution:
  ::解决方案 :

  播放段落

  Domain:  $\begin{array}{r}x\in [-3,2]\end{array}$
  ::域名: x[- 3, 2]

  播放段落

  Range:  $\begin{array}{r}y\in [-2,3]\end{array}$
  ::范围:y[-2,3]

  播放段落

  Example 4
  ::例4

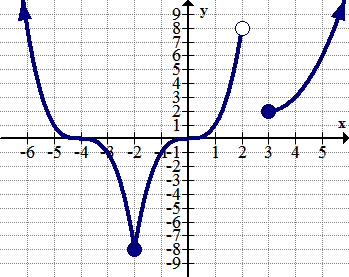
  播放段落

  Identify the domain and range of the following function: 
  ::确定下列函数的域和范围:

  

  
  

  播放段落

  Solution:
  ::解决方案 :

  播放段落

  Domain:  $\begin{array}{r}x\in [-3,-1)\cup [0,3)\end{array}$
  ::域 : x[- 3, - 1] [, 3]

  播放段落

  Range:  $\begin{array}{r}y\in [-2,\mathrm{\infty })\end{array}$
  ::范围: y[- 2, ]

  播放段落

  Note that the function seems to approach the vertical line $\begin{array}{r}x=-1\end{array}$  without actually reaching it. Also note the hole at the point (3, 1). This symbolizes that the domain excludes the  $\begin{array}{r}x\end{array}$ -value of 3. 
  ::注意该函数似乎接近垂直线 x\\\\1, 但没有实际达到它。 也注意点( 3, 1) 上的洞口, 这象征着域排除了 X 值 3 的 X 值 。

  播放段落

  Example 5
  ::例5

  播放段落

  Identify the domain and range of the following function written in a table:
  ::确定表格中写入的下列函数的域和范围:

  播放段落

  $$\begin{array}{r}\begin{array}{|cc|}\hline x& y\\ 0& 5\\ 1& 6\\ 2& 7\\ \frac{1}{2}& 6\\ \pi & \frac{\pi }{2}\\ \hline\end{array}\end{array}$$

  
  ::xy051627126+2

  播放段落

  Solution:
  ::解决方案 :

  播放段落

  The equation of the function may be hidden, but from the table you can determine the domain and range directly from the  $\begin{array}{r}x\end{array}$ - and  $\begin{array}{r}y\end{array}$ -values. It may be tempting to guess that other values could potentially work in the table, especially if the pattern is obvious. But this question doesn't ask what the function might or could be. It asks what is the stated domain and range. 
  ::函数的方程式可能是隐藏的, 但从表格中您可以确定域名, 并直接从 x 和 y 值中进行。 这可能诱人猜想其他值在表格中可能有效, 特别是如果图案是显而易见的。 但这个问题并不问函数可能或可能是什么。 它询问指定的域名和范围是什么 。

  播放段落

  Domain:  $\begin{array}{r}x\in \{0,1,2,\frac{1}{2},\pi \}\end{array}$
  ::域名: x0,1,2,12,

  播放段落

  Range:  $\begin{array}{r}y\in \{5,6,7,\frac{\pi }{2}\}\end{array}$
  ::范围:y 5,6,7,2}

  播放段落

  Note that the 2 sixes that appear in the table do not need to be written twice in the range. 
  ::请注意,表中列出的2个六分之2不必在幅度内写两次。

  播放段落

  Example 6
  ::例6

  播放段落

  Identify the domain of the following transformed functions:
  ::确定下列已转变功能的域名:

  播放段落

  a.  $\begin{array}{r}y=10\sqrt{2-x}-3\end{array}$
  ::a.y=102-x-3

  播放段落

  Solution:
  ::解决方案 :

  播放段落

  The expression  under the square root must be greater than or equal to 0:
  ::平方根下的表达式必须大于或等于 0 :

  播放段落

  $$\begin{array}{rl}2-x& \ge 0\\ -x& \ge -2\\ x& \le 2\end{array}$$

  
  ::2 -x=0 -x==2x=2

  播放段落

  Domain:  $\begin{array}{r}x\in (-\mathrm{\infty },2]\end{array}$
  ::域名: x(),2;

   

  播放段落

  b.  $\begin{array}{r}y=\frac{3x}{x^2+7x+12}\end{array}$
  ::b. y=3x22+7x+12

  播放段落

  Solution:
  ::解决方案 :

  播放段落

  The denominator cannot be equal to 0. First, find what values of  $\begin{array}{r}x\end{array}$ would make it equal to 0 and then you can exclude those values:
  ::分母不能等于 0。 首先, 找到 x 的什么值使其等于 0, 然后您就可以排除这些值 :

  播放段落

  $$\begin{array}{rl}{x}^2+7x+12& =0\\ (x+4)(x+3)& =0\\ x& =-4,-3\end{array}$$

  
  ::x2+7x+12=0(x+4)(x+3)=0x4-3

  播放段落

  Thus, the domain is all real numbers except -4 and -3.
  ::因此,除-4和-3外,域名都是真实数字。

  播放段落

  Domain:  $\begin{array}{r}x\in (-\mathrm{\infty },-4)\cup (-4,-3)\cup (-3,\mathrm{\infty })\end{array}$
  ::域 : x ,

   

  播放段落

  c.  $\begin{array}{r}y=-4\log (3x-9)+11\end{array}$
  ::c. y4log(3x--9)+11

  播放段落

  Solution:
  ::解决方案 :

  播放段落

  The expression in the logarithm must be strictly greater than 0: 
  ::对数中的表达式必须严格大于 0 :

  播放段落

  $$\begin{array}{rl}3x-9& >0\\ 3x& >9\\ x& >3\end{array}$$

  
  ::3x-9>03x>9x>3

  播放段落

  Domain:  $\begin{array}{r}x\in (3,\mathrm{\infty })\end{array}$
  ::域 : x( 3, )

  播放段落

  Example 7
  ::例7

  播放段落

  What is the domain and range of the sine wave?
  ::什么是正弦波的域和范围?

  播放段落

  Solution:
  ::解决方案 :

   

  播放段落

  Domain:  $\begin{array}{r}x\in (-\mathrm{\infty },\mathrm{\infty })\end{array}$
  ::域 : x(,)

  播放段落

  Range:  $\begin{array}{r}y\in [-1,1]\end{array}$
  ::范围:y[- 1,1]

  播放段落

  Summary
  ::摘要

  播放段落
  • Domain is the set of inputs for a function.  
    ::域是函数的一组输入。
  播放段落
  • Range is the set of outputs for a function. 
    ::范围是函数的一组输出。
  播放段落
  • Interval notation is used to describe groups of numbers, such as when describing domain and range. Intervals are either open or closed or both. 
    ::在描述数字组时,如在描述域和范围时,使用中间符号来表示数字组。中间符号要么是开放的,要么是封闭的,或者两者兼而有之。
  播放段落
  • Open intervals use parentheses and refer to intervals that do not include the endpoints.  
    ::开放间隔使用括号 , 并指不包括终点的间隔 。
  播放段落
  • Closed intervals use square or box brackets [ ] and refer to intervals that do include the endpoints. 
    ::封闭间隔使用方括号或框括号[ ],并指包含终点的间隔。
  播放段落
  • Braces or curly brackets  { } are used when the domain or range consists of discrete numbers and not an interval of values. 
    ::当域或范围由离散数字而不是一个数值间隔组成时,则使用括号或括号 {{}。
  播放段落
  • $\begin{array}{r}\in \end{array}$  is a symbol that means “ is an element of ." 
    ::代表「是元素的一部分」。
  播放段落
  • $\begin{array}{r}\cup \end{array}$  is a symbol that means union and is used to connect two groups. It is associated with the logical term OR. 
    ::是一个象征,意指工会,用来连接两个群体。它与逻辑术语OR有关。

  播放段落

  Review  
  ::回顾

  播放段落

  Find the domain and range of each graph:
  ::查找每个图形的域和范围 :

  1. 

  

  
  

  2.

   

  3.
  

  4.

  

  5.

  

  6.

  

  7.

  

   

  播放段落

  Given the table, find the domain and range:
  ::从表格中找到域名和范围:

  8.

  播放段落

  $$\begin{array}{r}\begin{array}{|cc|}\hline x& y\\ \text{-}2& 7\\ 3& 7\\ 2& 1\\ \frac{3}{4}& 5\\ \frac{\pi }{2}& \pi \\ \hline\end{array}\end{array}$$

  
  ::Xy-2737-21345___________________________________________________________________________________________________________________________________________________________________________________________

  播放段落

  Find the domain and range for the following functions:
  ::查找下列函数的域和范围:

  播放段落

  9.   $\begin{array}{r}y=-{\left(6x+1\right)}^2+4\end{array}$
  ::9. y( 6x+1) 2+4

  播放段落

  10.  $\begin{array}{r}y=\log (8x-4)\end{array}$
  ::y=log( 8x- 4)

  播放段落

  11.  $\begin{array}{r}y=\frac{5}{x^3-1}\end{array}$
  ::11. y=5x3-1

  播放段落

  12.  $\begin{array}{r}y=-3\sqrt{x+4}-1\end{array}$
  ::12. y3x+4-1

  播放段落

  13.  $\begin{array}{r}y=\frac{7}{x+6}-1\end{array}$
  ::13. y=7x+6-1

  播放段落

  14.  $\begin{array}{r}y=5\log (x^2-1)+4\end{array}$
  ::14. y=5log(x2-1)+4

  播放段落

  15.  $\begin{array}{r}y=\sqrt{4x^2-9}+6\end{array}$
  ::15.y=4x2-9+6

  播放段落

  16.  Bob had a summer job that paid $10 per hour, and he worked 20–25 hours every week. His weekly salary can be modeled by the equation $\begin{array}{r}S=10h\end{array}$ , where $\begin{array}{r}S\end{array}$  is his weekly salary and $\begin{array}{r}h\end{array}$  is the number of hours he worked per week. What is the independent variable for this problem? Describe the domain and range.
  ::16. Bob的暑期工作每小时10美元,每周工作20至25小时,每周工资以S=10h等式为模型,S=10h是每周工资,h是每周工作时数,这个问题的独立变量是什么?描述领域和范围。

  播放段落

  17. Tina’s car travels about 30 miles on one gallon of gas. She has between 10 and 12 gallons of gas in the tank. Find the domain and range of the function to calculate how far she can drive.
  ::17. 蒂娜的汽车在一加仑的气体上行驶约30英里,坦克内有10至12加仑的气体,找到功能的域域和范围以计算她能开多远。

  播放段落

  18. Joe and his three friends plan to go bowling and to bowl one or two games each. Each game costs $2.75. Find the domain and range of the function, calculating the cost of the trip.
  ::18. Joe和他的三个朋友计划去打保龄球,每人打一两场比赛,每场比赛费用为2.75美元,找出功能的域域和范围,计算旅行费用。

  播放段落

  Review (Answers)
  ::回顾(答复)

  播放段落

  Please see the Appendix.
  ::请参看附录。