Course: 2.6 功能图图的截断

Section outline

Select section General

Collapse Expand
General

Collapse all Expand all
- Select activity 新闻通告
  
  新闻通告 Forum
Select section 函数图截取

Collapse Expand
函数图截取
Introduction
::导言

The revenue collected by an apartment manager is given by $\begin{aligned} R (x) = (580 + 20 x) (50 - x), \end{aligned}$ where $\begin{aligned} x \end{aligned}$ is the number of $20 rent increases:
::公寓经理收取的收入由R(x)=(580+20x)(50-x)提供,其中x是增加的20美元租金:

In another section we used this example to discuss . Now, notice the points $\begin{aligned} (0, 29000) \end{aligned}$ and $\begin{aligned} (50, 0) \end{aligned}$ on the graph. These points convey special information. The first represents the revenue from rent of $29,000 per month before increasing the rent. The second point says that after fifty $20 increases (or an increase of $1000), all tenants will move and the rent revenue will be $0 per month. These special points are called intercepts .
::我们在另一节中用这个例子来讨论。现在,请注意图表上的点数(0,29000美元)和(50,0美元),这些点表示特殊信息。第一个点表示在增加租金之前每月租金收入29,000美元。第二个点表示在增加50美元(或增加1,000美元)之后,所有租户都将搬家,租金收入为每月0美元。这些特殊点被称为拦截。

Intercepts
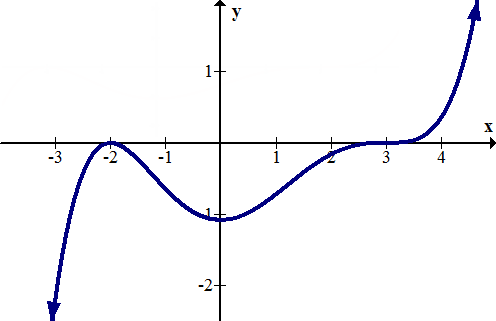
::拦截

An intercept in mathematics is the point where a function crosses the $\begin{aligned} x \end{aligned}$ - or $\begin{aligned} y \end{aligned}$ - axis. For example, identify the intercepts for the following graph:
::数学截取是函数通过 x 或 y 轴的点。例如,为下图标明截取次数:

The $\begin{aligned} x \end{aligned}$ -intercepts are $\begin{aligned} (- 2, 0) \end{aligned}$ and $\begin{aligned} (3, 0) \end{aligned}$ . The $\begin{aligned} y \end{aligned}$ -intercept is approximately $\begin{aligned} (0, - 1.1) \end{aligned}$ .
::x 拦截是 (-2,0) 和 (3,0) 。 y 拦截大约是 (0,-1.1)。

Zeros and roots are synonyms for the $\begin{aligned} x \end{aligned}$ -values where a function crosses or touches the $\begin{aligned} x \end{aligned}$ -axis. In order for a relation to pass the vertical line test and thus be a function, it must have only one $\begin{aligned} y \end{aligned}$ -intercept. However, it may have multiple $\begin{aligned} x \end{aligned}$ -intercepts.
::零和根是函数交叉或触摸 x 轴的 x 值的同义词。要通过垂直线测试从而成为函数,它必须只有一个 y 界面。但是, 它可能有多个 x 界面。

$\begin{aligned} x \end{aligned}$ -intercept
::x 拦截

The $\begin{aligned} x \end{aligned}$ -intercept is the point where the function crosses or touches the $\begin{aligned} x \end{aligned}$ -axis. The $\begin{aligned} x \end{aligned}$ -values of these points are also called roots and zeros of a function. They are found algebraically by setting $\begin{aligned} y = 0 \end{aligned}$ and solving for $\begin{aligned} x \end{aligned}$ .
::x 界面是函数交叉或接触 x 轴的点。这些点的X 值也称为函数的根和零。它们通过设置 y=0 和为 x 解析而找到代数。

$\begin{aligned} y \end{aligned}$ -intercept
::y 界面

The $\begin{aligned} y \end{aligned}$ -intercept is the point where the function crosses or touches the $\begin{aligned} y \end{aligned}$ -axis. This point is found by setting $\begin{aligned} x \end{aligned}$ to zero and solving for $\begin{aligned} y \end{aligned}$ .
::y 界面是函数交叉或接触 y 轴的点。此点通过将 x 设置为零和为 y 解析找到。

Play, Learn, Interact, and Explore Intercepts:
::玩耍、学习、互动和探索拦截:

Examples
::实例

Example 1
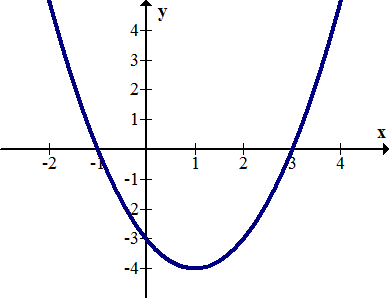
::例1

What are the zeros and $\begin{aligned} y \end{aligned}$ -intercept for the parabola $\begin{aligned} y = x^{2} - 2 x - 3 \end{aligned}$ ?
::参数 y=x2-2x-3 的零和 Y 界面是什么 ?

Solution:
::解决方案 :

Method 1: Solution using a graph:
::方法1:使用图表的解决方案:

The zeros are at $\begin{aligned} x = - 1, 3 \end{aligned}$ . The $\begin{aligned} y \end{aligned}$ -intercept is at (0, -3).
::零位值为 x1,3。 Y 拦截值为 0, - 3 。

Method 2: Solution using algebra:
::方法2:用代数解析:

When $\begin{aligned} y = 0 \end{aligned}$ , substitute 0 for $\begin{aligned} y \end{aligned}$ to find zeros.
::当 Y=0 时, 以 0 代替 y 找到零。

$\begin{aligned} 0 = x^{2} - 2 x - 3 = (x - 3) (x + 1) \end{aligned}$
::0=x2-2-2x-3=(x-3)(x+1)

$\begin{aligned} y = 0, x = 3, - 1 \end{aligned}$
::y=0,x=3,-1

The zeros are -1 and 3 and can be found at the $\begin{aligned} x \end{aligned}$ -intercepts (-1, 0) and (3, 0).
::零为-1和3,可在X-截取器(-1,0)和(3,0)中找到。

When $\begin{aligned} x = 0 \end{aligned}$ , substitute 0 for $\begin{aligned} x \end{aligned}$ to find the $\begin{aligned} y \end{aligned}$ -intercept.
::当 x=0 时, 以 0 代替 x 查找 Y 接口。

$\begin{aligned} y = (0)^{2} - 2 (0) - 3 = - 3 \end{aligned}$
::y=(0)2-2-2(0)-33

$\begin{aligned} x = 0, y = - 3 \end{aligned}$
::x=0,y3

The $\begin{aligned} y \end{aligned}$ -intercept is at (0, -3).
::y 界面为 0, - 3 。

Example 2
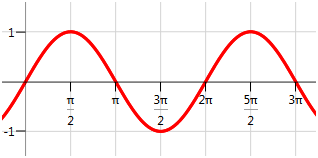
::例2

Identify the zeros and $\begin{aligned} y \end{aligned}$ -intercepts for the sine function:
::识别正弦函数的零和 Y 界面 :

Solution:
::解决方案 :

The $\begin{aligned} y \end{aligned}$ -intercept is (0, 0). There are four zeros visible on this portion of the graph. The sine graph is periodic and repeats in both directions. In order to capture every $\begin{aligned} x \end{aligned}$ -intercept, a pattern for the zeros should be identified.
::y 界面是 (0, 0) 。图形的这一部分有 4 个零可见。正弦图是周期性的, 双向重复。为了捕捉每个 x 界面, 需要为零确定一个模式。

The visible zeros are $\begin{aligned} 0, π, 2 π, \end{aligned}$ and $\begin{aligned} 3 π \end{aligned}$ . The pattern is that there is an $\begin{aligned} x \end{aligned}$ -intercept every multiple of $\begin{aligned} π \end{aligned}$ , including negative multiples. The matching zero values can be described in this way:
::可见零是 0, , 2, 和 3。模式是 X 拦截的倍数, 包括负倍数。匹配的零值可以这样描述 :

The zeros are $\begin{aligned} n π \end{aligned}$ , where $\begin{aligned} n \end{aligned}$ is an integer $\begin{aligned} {0, \pm 1, \pm 2, \dots} \end{aligned}$ .
::零是 n, n是整数 {0, 1, 2,...} 。

Example 3
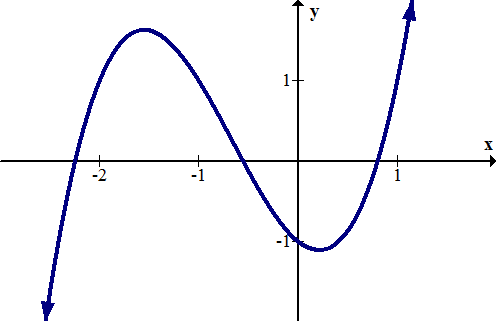
::例3

Identify the intercepts and zeros of the function $\begin{aligned} f (x) = \frac{1}{100} (x - 3)^{3} (x + 2)^{2} \end{aligned}$ .
::识别函数 f( x) = 1100( x-3) 33( x+2) 的拦截数和零。

Solution:
::解决方案 :

To find the value of $\begin{aligned} y \end{aligned}$ for the $\begin{aligned} y \end{aligned}$ -intercept, substitute 0 for $\begin{aligned} x \end{aligned}$ :
::要找到 Y 的 Y 值, 以 x 0 代替 x :

$\begin{aligned} y = \frac{1}{100} (0 - 3)^{3} (0 + 2)^{2} = \frac{1}{100} (- 27) (4) = - \frac{108}{100} = - 1.08 \end{aligned}$
::y=1100(0-3)3(0+2)2=1100(-27)(4)1081001.08

To find the $\begin{aligned} x \end{aligned}$ -intercepts, substitute 0 for $\begin{aligned} y \end{aligned}$ :
::要找到 X 界面, 替换 0 替换 y :

$\begin{aligned} 0 = \frac{1}{100} (x - 3)^{3} (x + 2)^{2} \end{aligned}$
::0=1100(x-3-3)3(x+2)2

By the zero product property , which states that if the product of a set of factors equals zero then one or more of the factors must equal zero, $\begin{aligned} x - 3 = 0 \end{aligned}$ or $\begin{aligned} x + 2 = 0 \end{aligned}$ .
::根据零产品属性,该属性规定,如果一组因数的产值等于零,则一个或多个因数必须等于零,x-3=0或x+2=0。

$\begin{aligned} x = 3, - 2 \end{aligned}$
::x=3,-2,x=3,-2

Thus, the $\begin{aligned} y \end{aligned}$ -intercept is (0, -1.08), and the zeros are 3 and -2, which can be found at the $\begin{aligned} x \end{aligned}$ -intercepts: (3, 0) and (-2, 0).
::因此, Y 界面是 (0, -1.08) , 零是 3 和 -2, 可在 x 界面中找到 : (3, 0) 和 (2, 0) 。

Example 4
::例4

Determine the $\begin{aligned} x \end{aligned}$ -intercepts and $\begin{aligned} y \end{aligned}$ -intercept of the following function, using algebra: $\begin{aligned} f (x) = (x + 3)^{2} (x - 2) \end{aligned}$ .
::使用代数( f( x) = (x+3) 2(x-2) 确定下列函数的 x 界面和 Y 界面: f( x) = (x+3) 2(x-2) 。

Solution:
::解决方案 :

To find the $\begin{aligned} y \end{aligned}$ -intercept, substitute 0 for $\begin{aligned} x \end{aligned}$ :
::要找到 Y 接口, x 的替代值 0 :

$\begin{aligned} y = (0 + 3)^{2} (0 - 2) = 3^{2} \cdot (- 2) = 9 \cdot (- 2) = - 18 \end{aligned}$

::y= (0+3) 2(0-2) = 32(-2) = 9(-2) 18

The $\begin{aligned} y \end{aligned}$ -intercept is (0, -18).
::Y 拦截是 (0, -18) 。

To find the $\begin{aligned} x \end{aligned}$ -intercepts, substitute 0 for $\begin{aligned} y \end{aligned}$ :
::要找到 X 界面, 替换 0 替换 y :

$\begin{aligned} 0 = (x + 3)^{2} (x - 2) \end{aligned}$

::0=(xx+3)2(x-2)

By the zero product property, $\begin{aligned} x + 3 = 0 \end{aligned}$ or $\begin{aligned} x - 2 = 0 \end{aligned}$ .
::按零产品属性, x+3=0 或 x-2=0 。

$\begin{aligned} x = - 3, 2 \end{aligned}$

::x3,2

The $\begin{aligned} x \end{aligned}$ -intercepts are (-3, 0) and (2, 0).
::x 界面是 (3, 0) 和 (2, 0) 。

Example 5
::例5

Determine the roots and $\begin{aligned} y \end{aligned}$ -intercept of the following function, using algebra or a graph:
::使用代数或图表确定以下函数的根和 Y interview:

$\begin{aligned} f (x) = x^{4} + 3 x^{3} - 7 x^{2} - 15 x + 18 \end{aligned}$
:x) =x4+3x3- 7x2- 15x+18

Solution:
::解决方案 :

To find the $\begin{aligned} y \end{aligned}$ -intercept, substitute 0 for $\begin{aligned} x \end{aligned}$ :
::要找到 Y 接口, x 的替代值 0 :

$\begin{aligned} y = 0^{4} + 3 \cdot 0^{3} - 7 \cdot 0^{2} - 15 \cdot 0 + 18 = 18 \end{aligned}$
::y=04+303-702-15°0+18=18

The $\begin{aligned} y \end{aligned}$ -intercept is (0, 18).
::Y 界面是 (0, 18) 。

By graphing $\begin{aligned} f (x) = x^{4} + 3 x^{3} - 7 x^{2} - 15 x + 18, \end{aligned}$ the $\begin{aligned} x \end{aligned}$ -intercepts are (2, 0), (1, 0) and (-3, 0), so the roots are 2, 1, and -3.
::通过图形 f(x) =x4+3x3- 7x2- 15x+18, x- 截取为(2, 0) (1, 0) 和 (3, 3, 0) , 所以根是 2, 1 和 - 3 。

Example 6
::例6

Determine the intercepts of the following function graphically:
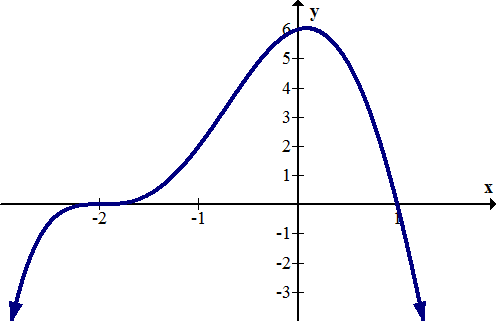
::以图形方式确定以下函数的拦截量:

Solution:,
::解决方案:

The $\begin{aligned} y \end{aligned}$ -intercept is approximately (0, -1). The $\begin{aligned} x \end{aligned}$ -intercepts are approximately (-2.3, 0), (-0.6, 0) and (0.8, 0). When finding values graphically, answers are always approximate. Exact answers need to be found analytically.
::y 界面大约为 0, - 1 。 x 界面大约为 (- 2.3, 0, 0, 0) 和 (-0.6, 0) 和 (0. 8, 0) 。以图形方式查找数值时, 答案总是大致的。精确答案需要用分析方式找到。

Summary
::摘要

Zeros and roots are synonyms for the $\begin{aligned} x \end{aligned}$ -values where a function crosses the $\begin{aligned} x \end{aligned}$ -axis.
::零和根是函数交叉 x 轴的 x 值的同义词。

An $\begin{aligned} x \end{aligned}$ -intercept i s the point where the graph of a function crosses or touches the $\begin{aligned} x \end{aligned}$ -axis.
::x 界面是函数图形交叉或触碰 x 轴的点。

A $\begin{aligned} y \end{aligned}$ -intercept is the point where the graph of a function crosses or touches the $\begin{aligned} y \end{aligned}$ -axis.
::y 界面是函数图形交叉或触碰 y 轴的点。

Note that in order for a function to pass the vertical line test and thus be a function, it should only have one $\begin{aligned} y \end{aligned}$ -intercept. However, it may have multiple $\begin{aligned} x \end{aligned}$ -intercepts.
::请注意,为了让函数通过垂直线测试并因此成为函数,它只应有一个 Y 接口。但是,它可能有多个 x 接口。

Review
::回顾

1. Determine the zeros and $\begin{aligned} y \end{aligned}$ -intercept of the following function algebraically:
::1. 确定下列函数代数的0和Y中间值:

$\begin{aligned} f (x) = (x + 1)^{3} (x - 4) \end{aligned}$
:xx) = (x+1) 3(x- 4)

2. Determine the roots and $\begin{aligned} y \end{aligned}$ -intercept of the following function using algebra or a graph:
::2. 使用代数或图表确定下列函数的根和 Y 界面:

$\begin{aligned} g (x) = x^{4} - 2 x^{3} - 7 x^{2} + 20 x - 12 \end{aligned}$
::g(x) =x4- 2x3- 7x2+20x- 12

3. Determine the intercepts of the following function graphically:
::3. 以图形方式确定以下函数的拦截量:

Find the intercepts for each of the following functions:
::查找以下每个函数的拦截功能:

4. $\begin{aligned} y = x^{2} \end{aligned}$
::4. y=x2

5. $\begin{aligned} y = x^{3} \end{aligned}$
::5. y=x3

6. $\begin{aligned} y = \log x \end{aligned}$
::6.y=logx

7. $\begin{aligned} y = \frac{1}{x} \end{aligned}$
::7.y=1x

8. $\begin{aligned} y = 2^{x} \end{aligned}$
::8. y=2x

9. $\begin{aligned} y = \sqrt{x} \end{aligned}$
::9.y=x 9y=x

10. Are there any functions without a $\begin{aligned} y \end{aligned}$ -intercept? Explain.
::10. 是否有任何功能没有y-intermissions?解释。

11. Are there any functions without an $\begin{aligned} x \end{aligned}$ -intercept? Explain.
::11. 是否有任何功能没有 X 拦截?解释。

12. Explain why it makes sense that an $\begin{aligned} x \end{aligned}$ -intercept of a function is also called a “zero” of the function.
::12. 解释为什么一个函数的X拦截也称为函数的 " 零 " 是有道理的。

Determine the intercepts of the following functions using algebra or a graph:
::使用代数或图表确定以下函数的截取次数:

13. $\begin{aligned} h (x) = x^{3} - 6 x^{2} + 3 x + 10 \end{aligned}$
::13. h(x) =x3 - 6x2+3x+10

14. $\begin{aligned} j (x) = x^{2} - 6 x - 7 \end{aligned}$
::14. j(x)=x2-6x-7

15. $\begin{aligned} k (x) = 4 x^{4} - 20 x^{3} - 3 x^{2} + 14 x + 5 \end{aligned}$
::15. kk(x)=4x4-20x3-3-3x2+14x+5

Review (Answers )
::回顾(答复)

Please see the Appendix.
::请参看附录。

Section outline

General

函数图截取

Introduction ::导言

Intercepts ::拦截

x -intercept ::x 拦截

y -intercept ::y 界面

Examples ::实例

Example 2 ::例2

Example 3 ::例3

Example 4 ::例4

Example 5 ::例5

Example 6 ::例6

Summary ::摘要

Review ::回顾

Review (Answers ) ::回顾(答复)

Introduction
::导言

Intercepts
::拦截

$\begin{aligned} x \end{aligned}$ -intercept
::x 拦截

$\begin{aligned} y \end{aligned}$ -intercept
::y 界面

Examples
::实例

Example 2
::例2

Example 3
::例3

Example 4
::例4

Example 5
::例5

Example 6
::例6

Summary
::摘要

Review
::回顾

Review (Answers )
::回顾(答复)