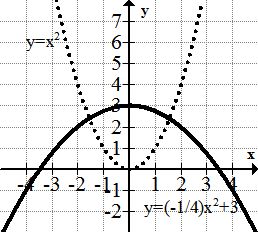Course: 2.8 图形转换 | The Way To Learn

Section outline

Select section General

Collapse Expand
General

Collapse all Expand all
- Select activity 新闻通告
  
  新闻通告 Forum

图形转换

Introduction
::导言

The basic families of functions provide a good starting point to analyze functions, and g reater depth can be added to their study by adapting the functions to specific situations. In this section, we'll explore methods of adapting functions, which help us to understand scenarios like this:
::功能的基本构成为分析功能提供了一个良好的起点,通过根据具体情况调整功能,可以在其研究中增加更大的深度。在本节中,我们将探索调整功能的方法,这有助于我们理解这样的情况:

C onsider the average annual cost of a new refrigerator. Suppose the cost of the refrigerator is spread out over its lifespan . If the price of the refrigerator is $900 and the operating cost is $175 per year, the average annual cost is reduced each year that we keep the refrigerator.
::如果冰箱的价格是900美元,而运作成本是每年175美元,则冰箱的年平均成本每年会减少。

lesson content

This function assumes that repair expenses are included in the operating cost.
::这项职能假定修理费用包括在业务费用中。

Average Annual Cost of a New Refrigerator
$\begin{aligned} t \end{aligned}$ (years)	Cost: $\begin{aligned} C (t) = \frac{900}{t} + 175 \end{aligned}$ ($)
1	1,075
5	355
15	235
20	220

The graph of the cost resembles one branch of the reciprocal graph. Notice that as the years $\begin{aligned} t \end{aligned}$ increase, the cost approaches a horizontal line rather than the axis, as it did in the parent graph . I n the 25th year, the average annual cost of the purchase price is so small that our operating cost comprises most of the expense.
::成本图与对等图表的一个分支相似。请注意,随着岁月的增加,成本接近水平线而不是轴线,就像在母图中所做的那样。在第25年,购买价格的平均年成本太小,以至于我们的业务成本占了大部分支出。

The techniques we will explore to adapt the parent functions to a wider variety of functions are:
::我们将探索如何使母功能适应更广泛的各种功能,即:

Shifting ( vertically and horizontally)
::移动(纵向和横向)

Stretching (vertically and horizontally)
::伸展( 垂直和水平伸展)

Reflecting (across the $\begin{aligned} x \end{aligned}$ - or $\begin{aligned} y \end{aligned}$ -axis )
::反射 (横过 X 或 Y 轴)

Vertical and Horizontal Shifting
::垂直和水平移动

Suppose that $\begin{aligned} c, d > 0 \end{aligned}$ . If the graph of $\begin{aligned} f (x) \end{aligned}$ is known, to graph:
::假设 c,d>0.。如果已知 f(x) 的图形,请用图表表示:

$\begin{aligned} y = f (x) + d \end{aligned}$ , shift the graph of $\begin{aligned} f (x) \end{aligned}$ up $\begin{aligned} d \end{aligned}$ units.
::y=f(x)+d, 移动 f(x) 上方 d 单位的图形。

$\begin{aligned} y = f (x) - d \end{aligned}$ , shift the graph of $\begin{aligned} f (x) \end{aligned}$ down $\begin{aligned} d \end{aligned}$ units.
::y=f(x)-d,将 f(x) 下方 d 单位的图形移动。

$\begin{aligned} y = f (x + c) \end{aligned}$ , shift the graph of $\begin{aligned} f (x) \end{aligned}$ left $\begin{aligned} c \end{aligned}$ units.
::y=f( x+c), 移动 f( x) 左 C 单位的图形。

$\begin{aligned} y = f (x - c) \end{aligned}$ , shift the graph of $\begin{aligned} f (x) \end{aligned}$ right $\begin{aligned} c \end{aligned}$ units.
::y=f(x-c), 移动 f(x) 右边 c 单位的图形。

This process is demonstrated in the following video:
::以下视频展示了这一进程:

Vertical and Horizontal S tretching and Shrinking
::垂直和水平伸展和缩小

If the graph of $\begin{aligned} f (x) \end{aligned}$ is known, to graph:
::如果 f( x) 的图形已知, 则用图形表示 :

$\begin{aligned} y = a f (x) \end{aligned}$ :
1. If $\begin{aligned} a > 1 \end{aligned}$ , stretch the graph vertically by a factor of $\begin{aligned} a \end{aligned}$ .
  ::如果 a>1, 则以 a 的因数垂直延伸图形。
2. If $\begin{aligned} 0 < a < 1 \end{aligned}$ , s hrink the graph vertically by a factor of $\begin{aligned} a \end{aligned}$ .
  ::如果 0<a<1, 则将图形垂直缩小为 a 的因数。
::y=af(x) : 如果 a>1, 则将图形垂直延伸为 a 系数。如果 0 < a < 1, 则将图形垂直缩小为 a 系数。

$\begin{aligned} y = f (b x) \end{aligned}$
1. If $\begin{aligned} b > 1 \end{aligned}$ , shrink the graph horizontally by a factor of $\begin{aligned} b \end{aligned}$ .
  ::如果 b>1, 则水平将图形缩小为 b 系数。
2. If $\begin{aligned} 0 < b < 1 \end{aligned}$ , stretch the graph horizontally by a factor of $\begin{aligned} \frac{1}{b} \end{aligned}$ .
  ::如果 0<b<1, 则将图形水平拉伸1b系数。
::y=f(bx) 如果 b>1, 则水平将图形缩小为 b 系数。如果 0 <b < 1, 水平将图形拉伸为 1b 系数。

Note that all horizontal transformations are found inside the function $\begin{aligned} f (b x) \end{aligned}$ or $\begin{aligned} f (x \pm c), \end{aligned}$ and all vertical transformations are outside the function $\begin{aligned} a f (x) \pm d \end{aligned}$ .
::请注意,所有水平变换都在函数 f(bx) 或 f(x) {c) 中找到,所有垂直变换均在函数 af(x) {d) 之外。

This process is demonstrated in the following video:
::以下视频展示了这一进程:

Reflecting across the $\begin{aligned} x \end{aligned}$ - or $\begin{aligned} y \end{aligned}$ -axis
::反射 X 或 Y 轴

If the graph of $\begin{aligned} f (x) \end{aligned}$ is known, to graph:
::如果 f( x) 的图形已知, 则用图形表示 :

$\begin{aligned} y = - f (x) \end{aligned}$ , reflect the graph across the $\begin{aligned} x \end{aligned}$ -axis.
::yf(x), 显示横跨 x 轴的图形。

$\begin{aligned} y = f (- x) \end{aligned}$ , reflect the graph across the $\begin{aligned} y \end{aligned}$ -axis.
::y=f( - x),在 Y 轴上方显示图形。

Order of Transformations
::变换顺序

The order of each transformation is important. When a function involves more than one transformation, complete the transformations according to the . Often, as in the case of $\begin{aligned} y = a f (b (x - h)) + d, \end{aligned}$ this results in:
::每次变换的顺序很重要。当函数涉及不止一次变换时, 请根据 . 完成变换。通常, 如y=af( b( x- h)) +d , 这导致 :

Horizontal shift
::水平转换

Vertical and horizontal stretching or shrinking
::垂直和水平伸展或缩小

Reflecting over an axis
::反射在轴上

Vertical shift
::垂直移动

Practice these transformations using the following interactive activities:
::利用下列交互式活动进行这些转变:

Vertical and Horizontal Shift Activity:
::垂直和水平倾移活动 :

Stretching and Shrinking Activity:
::伸展和缩小活动 :

Examples
::实例

Example 1
::例1

Graph $\begin{aligned} y = 1 + \sqrt{x - 2} \end{aligned}$ .
::图y=1+x-2。

Solution:
::解决方案 :

The basic graph is $\begin{aligned} y = \sqrt{x} \end{aligned}$ . To create the requested graph, this graph is first shifted to the right 2 units and up 1 unit:
::基本图形是 y=x。要创建所要求的图形,此图首先移到右侧的 2 个单位, 上移 1 个单位 :

Example 2
::例2

Graph $\begin{aligned} y = 3 \sqrt{\frac{1}{2} x} \end{aligned}$ .
::图y=312x。

Solution:
::解决方案 :

The basic graph is $\begin{aligned} y = \sqrt{x} \end{aligned}$ . To create the requested graph, this graph is stretched vertically by a factor of 3 and horizontally by a factor of 2:
::基本图形是 y=x。要创建所要求的图形,此图将垂直伸展3 倍,水平伸展2 倍。

Example 3
::例3

Graph $\begin{aligned} y = - 1 - \sqrt{- x} \end{aligned}$ .
::图表 y1x。

Solution
::解决方案

The basic graph is $\begin{aligned} y = \sqrt{x} \end{aligned}$ . For this example, the order that each transformation is applied is important. Starting with the innermost level, reflect the graph across the $\begin{aligned} y - \end{aligned}$ axis, then reflect across the $\begin{aligned} x - \end{aligned}$ axis, then shift down 1 unit:
::基本图形是 y=x。对于这个示例, 每次转换应用的顺序是重要的。从最深层开始, 将图形反射到 y - 轴, 然后反射到 x - 轴, 然后向下移动 1 个单位 :

Example 4
::例4

Describe the transformation and graph: $\begin{aligned} f (x) = {(3 x - 6)}^{2} \end{aligned}$
::描述变换和图形: f( x) =( 3x- 6) 2

Solution:
::解决方案 :

The basic graph is $\begin{aligned} y = x^{2} \end{aligned}$ . First, separate the horizontal shrink from the horizontal shift by factoring $\begin{aligned} f (x) = {(3 (x - 2))}^{2} \end{aligned}$ . The transformations are (in order) shift horizontally right 2 units, and shrink horizontally by a factor of $\begin{aligned} \frac{1}{3} \end{aligned}$ :
::基本图是 y=x2. 首先,通过乘数 f(x) = (3(x)-2) 2 将水平缩进与水平变化分开。变换为( 按顺序) 水平向右移动 2 单位, 水平向缩进13 倍 :

lesson content

Example 5
::例5

Describe the following transformation and graph: $\begin{aligned} y = - \frac{1}{4} x^{2} + 3 \end{aligned}$
::描述以下变换和图示: y14x2+3

Solution:
::解决方案 :

The basic graph is $\begin{aligned} y = x^{2} \end{aligned}$ . Using the quadratic function, the graph shrinks vertically by $\begin{aligned} \frac{1}{4} \end{aligned}$ , then it is reflected across the $\begin{aligned} x \end{aligned}$ -axis and shifted up by 3 units:
::基本图形是 y=x2. 使用二次函数,图形垂直缩缩14,然后在 X 轴上方反射,向上移动3个单位:

lesson content

Example 6
::例6

Recall the question from the Introduction. The function $\begin{aligned} C (t) = \frac{900}{t} + 175 \end{aligned}$ is related to the basic family of the reciprocal function $\begin{aligned} y = \frac{1}{x} . \end{aligned}$ It is adapted to model the annual cost of the refrigerator with a vertical stretch of 900 units (the cost of the refrigerator), and then shifted vertically by 175 units (the annual operating cost). Since the basic function approached the x-axis as x increased, the cost function approaches the horizontal line, y = 175 as t increases. In other words, the graph shows that as the refrigerator's age increases, the annual cost of purchasing the refrigerator decreases.
::回顾导言中的问题。函数C(t)=900t+175与对等函数y=1x的基本家庭有关。它经过调整,以模拟冰箱的年成本,垂直延伸900个单位(冰箱的成本),然后垂直移动175个单位(年度运行成本)。由于基本功能随着x增加而接近x轴,成本功能随着增加而接近水平线,y=175。换句话说,图表显示,随着冰箱年龄的增加,购买冰箱的年度成本下降。

Example 7
::例7

a) Describe the following transformation in words: $\begin{aligned} g (x) \end{aligned}$ is transformed to $\begin{aligned} 2 g (- x) \end{aligned}$ : $\begin{aligned} g (x) \to 2 g (- x) \end{aligned}$ .
:a) 用文字描述以下转换: g(x) 改为 2g(x) : g(x) =2g(x) =2g(x) =2g(x)。

Solution:
::解决方案 :

Vertical stretch of $\begin{aligned} g (x) \end{aligned}$ by a factor of 2 and a reflection across the $\begin{aligned} y \end{aligned}$ -axis.
::垂直伸展 g( x) 乘以 2, 反射横跨 Y 轴。

b) Write the expression for the transformation that would change $\begin{aligned} h (x) \end{aligned}$ in the following ways:
:b) 以下列方式写出改变h(x)的变换表达式:

Vertical compression (shrink) by a factor of 3
::垂直压缩(缩小) 3 乘以 3

Vertical shift down 4 units
::垂直向下移动 4 个单位

Horizontal shift right 5 units
::水平向右转移 5 个单位

Solution:
::解决方案 :

$\begin{aligned} \frac{1}{3} h (x - 5) - 4 \end{aligned}$
::13h(x-5-5)-4

c) Write the equation for the transformation that would change $\begin{aligned} f (x) \end{aligned}$ in the following ways:
:c) 写出转换方程式,以下列方式改变f(x):

Horizontal stretch by a factor of 4 and a horizontal shift 3 units to the right
::水平伸展以乘以 4 和水平向右移动 3 单位

Vertical reflection across the $\begin{aligned} x \end{aligned}$ axis and a shift down 2 units
::垂直反射横过 x 轴,向下移动 2 个单位

Solution :
::解决方案 :

$\begin{aligned} - f (\frac{1}{4} (x - 3)) - 2 \end{aligned}$ or $\begin{aligned} - f (\frac{1}{4} x - \frac{3}{4}) - 2 \end{aligned}$
::-f(14(x-3))-2或-f(14x-34)-2

Review
::回顾

Describe the following transformations in words:
::以文字描述下列变换:

1. $\begin{aligned} g (x) \to - g (- x) \end{aligned}$
::1. g(x)__________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

2. $\begin{aligned} f (x) \to - f (x + 3) \end{aligned}$
::2. f(x)f(x+3)

3. $\begin{aligned} h (x) \to h (x + 1) - 2 \end{aligned}$
::3.h(x+1)-2

4. $\begin{aligned} j (x) \to j (- x + 3) \end{aligned}$
::4. j(xx)j(-x+3)

5. $\begin{aligned} k (x) \to - k (2 x) \end{aligned}$
::5. k(x)\\\ k( 2x)

6. $\begin{aligned} f (x) \to 4 f (\frac{1}{2} x + 1) \end{aligned}$
::6. f(x)4f(12x+1)

7. $\begin{aligned} g (x) \to - 3 g (x - 2) - 2 \end{aligned}$
::7. g(x)_________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

8. $\begin{aligned} h (x) \to 5 h (x + 1) \end{aligned}$
::8. h(x)5h(x+1)

9. Write the equation for the transformation that would change $\begin{aligned} h (x) \end{aligned}$ in the following ways:
::9. 以下列方式写出改变h(x)的转换方程式:

Vertical stretch by a factor of 2
::垂直伸展乘以 2

Vertical shift up 3 units
::垂直向上移动 3 个单位

Horizontal shift right 2 units
::水平向右移动 2 个单位

10. Write the equation for the transformation that would change $\begin{aligned} f (x) \end{aligned}$ in the following ways:
::10. 以下列方式写出改变f(x)的变异方程:

Vertical reflection across the $\begin{aligned} x \end{aligned}$ axis
::x轴垂直反射

Vertical shift down 1 unit
::垂直向下移动 1 个单位

Horizontal shift left 2 units
::水平向左移 2 个单位

11. Write the equation for the transformation that would change $\begin{aligned} g (x) \end{aligned}$ in the following ways:
::11. 以下列方式写出改变 g(x) 的变异方程:

Vertical compression by a factor of 4
::垂直压缩 4 乘以 4

Reflection across the $\begin{aligned} y \end{aligned}$ axis
::反射在 y 轴的反射

12. Write the equation for the transformation that would change $\begin{aligned} j (x) \end{aligned}$ in the following ways:
::12. 以下列方式写出改变j(x)的转换方程式:

Horizontal compression by a factor of 3
::水平压缩乘以 3

Vertical shift up 3 units
::垂直向上移动 3 个单位

Horizontal shift right 2 units
::水平向右移动 2 个单位

13. Write the equation for the transformation that would change $\begin{aligned} k (x) \end{aligned}$ in the following ways:
::13. 以下列方式写出改变 k(x) 的转换方程式:

Horizontal stretch by a factor of 4
::水平拉伸 4 乘以 4

Vertical shift up 3 units
::垂直向上移动 3 个单位

Horizontal shift left 1 unit
::水平向左倾向左1单位

14. Write the equation for the transformation that would change $\begin{aligned} h (x) \end{aligned}$ in the following ways:
::14. 以下列方式写出改变h(x)的转换方程式:

Vertical compression by a factor of 2
::垂直压缩乘以 2

Horizontal shift right 3 units
::水平向右移动 3 个单位

Reflection across the $\begin{aligned} y \end{aligned}$ axis
::反射在 y 轴的反射

15. Write the equation for the transformation that would change $\begin{aligned} f (x) \end{aligned}$ in the following ways:
::15. 以下列方式写出改变f(x)的变异方程:

Vertical stretch by a factor of 5
::垂直伸展 5 乘以 5

Reflection across the $\begin{aligned} x \end{aligned}$ axis
::X轴反射

Review (Answers)
::回顾(答复)

Please see the Appendix.
::请参看附录。

Section outline

General

图形转换

Introduction ::导言

Vertical and Horizontal Shifting ::垂直和水平移动

Vertical and Horizontal S tretching and Shrinking ::垂直和水平伸展和缩小

Reflecting across the x - or y -axis ::反射 X 或 Y 轴

Order of Transformations ::变换顺序

Examples ::实例

Example 1 ::例1

Example 2 ::例2

Example 3 ::例3

Example 4 ::例4

Example 5 ::例5

Review ::回顾

Review (Answers) ::回顾(答复)

Introduction
::导言

Vertical and Horizontal Shifting
::垂直和水平移动

Vertical and Horizontal S tretching and Shrinking
::垂直和水平伸展和缩小

Reflecting across the $\begin{aligned} x \end{aligned}$ - or $\begin{aligned} y \end{aligned}$ -axis
::反射 X 或 Y 轴

Order of Transformations
::变换顺序

Examples
::实例

Example 1
::例1

Example 2
::例2

Example 3
::例3

Example 4
::例4

Example 5
::例5

Review
::回顾

Review (Answers)
::回顾(答复)