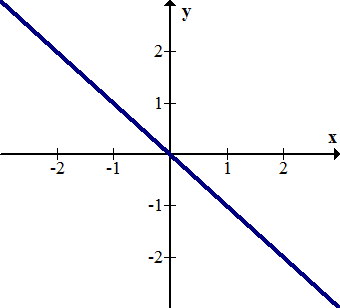Course: 2.12 职能组合和组成

Section outline

Select section General

Collapse Expand
General

Collapse all Expand all
- Select activity 新闻通告
  
  新闻通告 Forum
Select section 职能组合和组成

Collapse Expand
职能组合和组成
Introduction
::导言

A small art framing company hired a management consultant to analyze its revenue and expenses. The consultant delivered these mathematical functions:
::一家小型艺术设计公司雇用了一名管理顾问,分析其收入和支出。

Revenue: $\begin{aligned} R (x) = 300 x - \frac{x^{2}}{200}, \end{aligned}$ where $\begin{aligned} x \end{aligned}$ is number of units sold
::收入:R(x)=300x-x2200,其中x是出售的单位数

Cost: $\begin{aligned} C (x) = 500 + 175 x + .7 x^{2} - .00005 x^{3}, \end{aligned}$ where $\begin{aligned} x \end{aligned}$ is number of units produced
::成本:C(x)=500+175x+7x2-0.0005x3,其中x是生产的单位数

Net Revenue: $\begin{aligned} N (r) = 0.91 r, \end{aligned}$ where $\begin{aligned} r \end{aligned}$ is the amount of total revenue in dollars
::净收入:N(r)=0.91r,r为以美元计的总收入总额。

However, two problems surfaced. The consultant also needed:
::然而,出现了两个问题:顾问还需要:

A profit function (revenue versus cost)
::利润函数(收入与成本)

Net revenue based on the number of items sold
::按出售物品数量计算的净收入净额

In order to determine each of these items, the functions can be combined using function combinations. A function combination means simply combining two functions using the arithmetic operators $\begin{aligned} +, -, \cdot, and \div, \end{aligned}$ as long as the denominator function is not equal to 0.
::为了确定这些项中的每一项, 函数可以使用函数组合方式组合。函数组合意味着只要分母函数不等于 0, 则使用算术运算符+, -, , 和 + 和 + 组合两个函数。

Thus, profit can be created as an arithmetic combination of the revenue and cost functions:
::因此,利润可以作为收入和成本功能的算术组合产生:

$\begin{aligned} P (x) & = R (x) - C (x) \\ P (x) & = 300 x - \frac{x^{2}}{200} - (500 + 175 x + .7 x^{2} - .00005 x^{3}) \\ P (x) & = 125 x - .075 x^{2} + .00005 x^{3} - 500 \end{aligned}$

::P(x)=R(x)-C(x)-C(x)=300x-x2200-(500+175x+7x2-0.0005x3)P(x)=125x-.075x2+.00005x3-500

The 2nd combination of functions is more sophisticated. Now, to calculate net revenue (revenue after taxes) the company had to take two steps:
::第二套功能组合更为复杂。现在,为了计算净收入(税后收入),公司不得不采取两步:

Calculate revenue, based on the number sold.
::计算收入,根据售出数计算。

Take that value as input for the net revenue function, and calculate the final value.
::将此值作为净收入函数的输入值,然后计算最终值。

Net revenue based on the number sold can be created as a composition of net revenue and revenue as follows:
::以出售数量为基础的净收入可按净收入和净收入组成如下:

$\begin{aligned} (N \circ R) (x) & = N (R (x)) \\ = N (300 x - \frac{x^{2}}{200}) \\ = 0.91 (300 x - \frac{x^{2}}{200}) \\ = 273 x - .00455 x^{2} \end{aligned}$

:NR(x)=N(R(x))=N(300x-x2200)=0.91(300x-x2200)=273x-00455x2)

Now the two required functions are ready to use. These two functions were created from the original functions using either combinations or composition of functions.
::现在,需要的两项职能可以随时使用。这两项职能是利用职能的组合或构成从原有职能中产生的。

Play, Lean, and Explore Combining Functions:
::玩耍、倾斜和探索组合函数:

Function Composition
::职能构成构成

A composite function is a combination of two functions. Function composition can be thought of visually as a mapping from the domain to the range of the two functions. Function composition can also be thought of algebraically using function composition notation. The following video describes both ways of thinking about function composition:
::复合功能是两种功能的组合。可将功能构成视为从域到两个功能范围的直观映射。也可以将函数构成视为使用函数构成符号的代数。以下视频描述了两种功能构成的两种思维方式:

Function Composition Visually
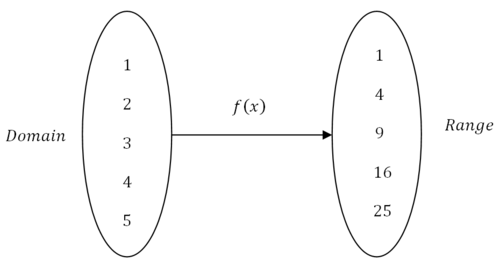
::职能构成

A common way to describe functions is a mapping from the domain to the range:
::描述函数的一种常见方式是绘制从域到范围的地图:

With function composition, the range of the 1st function becomes the domain of the 2nd function:
::随着函数的构成,第一个函数的范围成为第二个函数的域 :

Function Composition Notation
::函数构成说明

Function composition can also be thought of algebraically using function composition notation:
::职能构成也可以用职能构成的符号表示代数:

Function Composition Notation
::函数构成说明

$\begin{aligned} (g \circ f) (x) = g (f (x)) \end{aligned}$

On both sides of the equation , the $\begin{aligned} f \end{aligned}$ function is linked to the $\begin{aligned} x \end{aligned}$ , and thus operates on the $\begin{aligned} x \end{aligned}$ -values 1st. Then the result is inputted into the $\begin{aligned} g \end{aligned}$ function. Notice that you always work right to left in solving a function composition.
::在方程的两侧, f 函数与 x 相链接, 从而在 x 值 1 上运行。然后将结果输入 g 函数。注意您总是在解决函数构成时右向左工作。

Each of the following functions has a function composition within the function. For instance, in $\begin{aligned} j (x) \end{aligned}$ , the outer function could be $\begin{aligned} \sqrt{x} \end{aligned}$ and the inner function could be $\begin{aligned} x + 1 \end{aligned}$ :
::下列每项职能在职能内都有职能构成。例如,在j(x)中,外函数可以是x,内函数可以是x+1;

$\begin{aligned} f (x) = x^{2} - 1 \end{aligned}$

:xx)=x2-1

$\begin{aligned} h (x) = \frac{x - 1}{x + 5} \end{aligned}$

::h(x) =x - 1x+5

$\begin{aligned} g (x) = 3 e^{x} - x \end{aligned}$

::g( x) = 3ex- x

$\begin{aligned} j (x) = \sqrt{x + 1} \end{aligned}$

::j(x)=x+1

Examples
::实例

Example 1
::例1

Using the functions defined above, what is the function composition $\begin{aligned} g (h (x)) \end{aligned}$ ?
::使用上文定义的函数,函数构成g(h(x))是什么?

Solution:
::解决方案 :

Substitute $\begin{aligned} h (x) \end{aligned}$ into the $\begin{aligned} g \end{aligned}$ function for $\begin{aligned} x \end{aligned}$ :
::x 的 g 函数中替换 h( x) :

$\begin{aligned} \begin{aligned} g (h (x)) & = g (\frac{x - 1}{x + 5}) \\ = 3 e^{(\frac{x - 1}{x + 5})} - (\frac{x - 1}{x + 5}) \end{aligned} \end{aligned}$
::g(h(xx)=g(x-1x+5)=3e(x-1x+5)-(x-1x+5)

Example 2
::例2

Using the functions defined above, what is the function composition $\begin{aligned} f (j (h (g (x)))) \end{aligned}$ ?
::使用上文定义的函数,函数构成f(j(g(x)))是什么?

Solution:
::解决方案 :

There are many function compositions in this example. In these cases, begin composing the innermost functions 1st, and then continue to compose the functions working inside out. In this problem, 1st s ubstitute $\begin{aligned} g (x) \end{aligned}$ into the $\begin{aligned} h \end{aligned}$ function for $\begin{aligned} x \end{aligned}$ :
::在此示例中包含许多函数构成。在这种情况下, 开始组成最核心函数 1st, 然后继续组成正在运行的函数。在此问题上, 第一次将 g( x) 替换为 h 函数 x :

$\begin{aligned} h (g (x)) = \frac{3 e^{x} - x - 1}{3 e^{x} - x + 5} \end{aligned}$
::h( g(x)) = 3ex - x - 13ex - x+5

Next, consider $\begin{aligned} f (j (x)) \end{aligned}$ by substituting $\begin{aligned} j (x) \end{aligned}$ into $\begin{aligned} f (x) \end{aligned}$ :
::下一步,考虑f(j(x)),将j(x)改为f(x):

$\begin{aligned} f (j (x)) = {(\sqrt{x + 1})}^{2} - 1 = (x + 1) - 1 = x \end{aligned}$
::f( j( x) = (x+1) = (x+1) 2 - 1= (x+1) - 1=x

Notice how this composition simplifies to the variable . Thus, $\begin{aligned} f (j (h (g (x)))) = h (g (x)) \end{aligned}$ .
::注意该组成是如何简化到变量的。因此, f( j( h) (g(x))) =h( g(x) ) 。

Example 3
::例3

Show $\begin{aligned} f (h (x)) \neq h (f (x)) \end{aligned}$
::显示 f( h(x)) @ h(f(x))

Solution:
::解决方案 :

$\begin{aligned} f (h (x)) = f (\frac{x - 1}{x + 5}) = {(\frac{x - 1}{x + 5})}^{2} - 1 \end{aligned}$
::f(h(x)) = f(x-1x+5) = (x-1x+5) = (x-1x+5) 2-1

$\begin{aligned} h (f (x)) = h (x^{2} - 1) = \frac{(x^{2} - 1) - 1}{(x^{2} - 1) + 5} = \frac{x^{2} - 2}{x^{2} + 4} \end{aligned}$
::h(f(xx))=h(x2-1)=(x2-1)=(x2-1)-1-1(x2-1)-1(x2-1)+5=x2-2x2+4

To truly show they are not equal, it is best to find a specific counter example of a number where they differ. Sometimes algebraic expressions may look different, but are actually the same. You should notice that $\begin{aligned} f (h (x)) \end{aligned}$ is undefined when $\begin{aligned} x = - 5 \end{aligned}$ , because then there would be 0 in the denominator. $\begin{aligned} h (f (x)), \end{aligned}$ on the other hand, is defined at $\begin{aligned} x = - 5 \end{aligned}$ . Since the two function compositions differ, you can conclude: $\begin{aligned} f (h (x)) \neq h (f (x)) \end{aligned}$ .
::要真正显示它们不相等, 最好找到一个不同的数字的具体对应示例。有时代数表达式看起来可能不同, 但实际上是一样的。您应该注意, f( h( x)) 在 x% 5 时没有定义, 因为那样的话分母中就会有 0 。 h( f( x)) 在 x% 时, 定义在 x% 5 。由于两种函数的构成不同, 您可以得出 : f( h( x))\\\\\\ h( f( x) ) 。

For the next three example problems use the following functions:
::对于下三个例子,问题使用以下功能:

$\begin{aligned} f (x) = | x | \end{aligned}$
:fx)

$g(x)=e^x$

$h(x) = -x$

Example 4
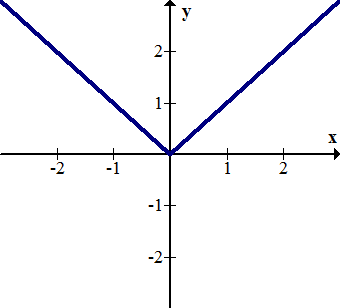
::例4

Compose $\begin{aligned} g (f (x)) \end{aligned}$ and graph the result. Describe the transformation.
::g(f(x)) 和图形结果。描述转换。

Solution:
::解决方案 :

$\begin{aligned} g (f (x)) = g (| x |) = e^{| x |} \end{aligned}$
::g( f( x)) = g( \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ x \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ g( f( x) ) \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \

The positive portion of the exponential graph has been reflected over the $\begin{aligned} y \end{aligned}$ -axis, and the negative portion of the exponential graph has been removed .
::指数图的正值部分已反映在 Y 轴上,指数图的负值部分已被删除。

Example 5
::例5

Compose $\begin{aligned} h (g (x)) \end{aligned}$ and graph the result. Describe the transformation.
::撰写 h( g( x) ) 并绘制结果图。描述转换。

Solution:
::解决方案 :

$\begin{aligned} h (g (x)) = h (e^{x}) = - e^{x} \end{aligned}$
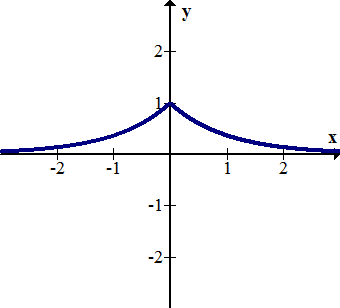
::h( g( x) ) =h( ex) \\ ex

The exponential graph has been reflected over the $\begin{aligned} x \end{aligned}$ -axis.
::指数图已经反射到 X 轴上。

Example 6
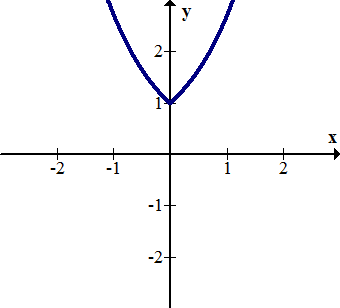
::例6

Compose $\begin{aligned} g (h (f (x))) \end{aligned}$ and graph the result. Describe the transformation.
::g(h(f(x))) 和图形结果。描述转换。

Solution :
::解决方案 :

$\begin{aligned} g (h (f (x))) = g (h (| x |)) = g (- | x |) = e^{- | x |} \end{aligned}$
::g( f( x) ) = g( h ) = g = g = e x = e x =

The negative portion of the exponential graph has been mirrored over the $\begin{aligned} y \end{aligned}$ -axis, and the positive portion of the exponential graph has been truncated.
::指数图的负部分反射到y轴上,指数图的正部分被缩短。

Summary
::摘要

New functions can be made from existing functions through arithmetic combinations or composition. The new functions can combine the effects of the original functions in one step.
::可以通过计算组合或组成,从现有功能中产生新的功能。新功能可将原有功能的效应合并为一个步骤。

Function composition is when there are two or more functions, and the range of the 1st function becomes the domain of the 2nd function.
::职能构成是指存在两个或两个以上职能,而第1个职能的范围成为第2个职能的领域。

Review
::回顾

For questions 1-9, use the following three functions: $\begin{aligned} f (x) = | x |, h (x) = - x, g (x) = (x - 2)^{2} - 3 \end{aligned}$ .
::对于问题1-9,使用以下三个函数:f(x)xx,h(x)x,g(x)=(x-2)2-3。

1. Determine $\begin{aligned} g (x) - h (x) . \end{aligned}$
::1. 确定 g(x)-h(x) 。

2. Graph $\begin{aligned} f (x), h (x) \end{aligned}$ and $\begin{aligned} g (x) \end{aligned}$ .
::2. 图f(x)、h(x)和g(x)。

3. Find $\begin{aligned} f (g (x)) \end{aligned}$ algebraically.
::3. 查找f(g(x))代数。

4. Graph $\begin{aligned} f (g (x)) \end{aligned}$ and describe the transformation.
::4. 图f(g(x))并说明变换情况。

5. Find $\begin{aligned} g (f (x)) \end{aligned}$ algebraically.
::5. 查找 g(f(x)) 代数。

6. Graph $\begin{aligned} g (f (x)) \end{aligned}$ and describe the transformation.
::6. 图g(f(x))和说明变换情况。

7. Find $\begin{aligned} h (g (x)) \end{aligned}$ algebraically.
::7. 查找h(g(x))代数。

8. Graph $\begin{aligned} h (g (x)) \end{aligned}$ and describe the transformation.
::8. 图h(g(x))并说明变换情况。

9. Find $\begin{aligned} g (h (x)) \end{aligned}$ algebraically.
::9. 查找 g(h(x))代数。

10. Graph $\begin{aligned} g (h (x)) \end{aligned}$ and describe the transformation.
::10. 图g(h(x))和说明变换情况。

For 10-16, use the following three functions: $\begin{aligned} j (x) = x^{2}, k (x) = | x |, m (x) = \sqrt{x} \end{aligned}$ .
::对于 10-16, 使用以下三个函数 : j( x) =x2, k( x) x , m( x) =x。

11. Determine $\begin{aligned} j (x) + m (x) . \end{aligned}$
::11. 确定j(x)+m(x)

12. Graph $\begin{aligned} j (x), k (x) \end{aligned}$ and $\begin{aligned} m (x) \end{aligned}$ .
::12. 图j(x)、k(x)和m(x).

13. Find $\begin{aligned} j (k (x)) \end{aligned}$ algebraically.
::13. 查找j(k(x))代数。

14. Graph $\begin{aligned} j (k (x)) \end{aligned}$ and describe the transformation.
::14. 图j(k(x)),说明变换情况。

15. Find $\begin{aligned} k (m (x)) \end{aligned}$ algebraically.
::15. 查找 k(m(xx)) 代数。

16. Graph $\begin{aligned} k (m (x)) \end{aligned}$ and describe the transformation.
::16. 图k(m(x)),说明变换情况。

17. Find $\begin{aligned} m (k (x)) \end{aligned}$ algebraically.
::17. 查找 m(k(x)) 代数。

18. Graph $\begin{aligned} m (k (x)) \end{aligned}$ and describe the transformation.
::18. 图m(k(x))并说明变换情况。

19. A toy manufacturer has a new product to sell. The number of units to be sold, n , is a function of the price, p, such that $\begin{aligned} n (p) = 30 - 25 p \end{aligned}$ . The revenue, r, earned from the sales is a function of the number of units sold, n, such that %20%3D%201000%20-%20%5Cfrac%7B1%7D%7B4%7Dn%5E2." style="box-sizing: border-box;"> $\begin{aligned} r (n) = 1000 - \frac{1}{4} n^{2} . \end{aligned}$ Find the function for revenue in terms of price, p .
::19. 玩具制造商要销售的新产品。要出售的单位数目,n,取决于价格,p,例如n(p)=30-25p。销售所得的收入,r,取决于售出的单位数目,n,r=1000-1400-1400n2.从价格上确定收入的函数,p。

Review (Answers )
::回顾(答复)

Please see the Appendix.
::请参看附录。

Section outline

General

职能组合和组成

Introduction ::导言

Function Composition ::职能构成构成

Function Composition Visually ::职能构成

Function Composition Notation ::函数构成说明

Function Composition Notation ::函数构成说明

Examples ::实例

Example 1 ::例1

Example 2 ::例2

Example 3 ::例3

For the next three example problems use the following functions: ::对于下三个例子,问题使用以下功能:

Example 4 ::例4

Example 5 ::例5

Solution: ::解决方案 :

Example 6 ::例6

Summary ::摘要

Review ::回顾

Review (Answers ) ::回顾(答复)

Introduction
::导言

Function Composition
::职能构成构成

Function Composition Visually
::职能构成

Function Composition Notation
::函数构成说明

Function Composition Notation
::函数构成说明

Examples
::实例

Example 1
::例1

Example 2
::例2

Example 3
::例3

For the next three example problems use the following functions:
::对于下三个例子,问题使用以下功能:

Example 4
::例4

Example 5
::例5

Solution:
::解决方案 :

Example 6
::例6

Summary
::摘要

Review
::回顾

Review (Answers )
::回顾(答复)