课程： 3.9 对合理职能的分析

章节大纲

选择节常规

折叠展开
常规

全部折叠展开全部
- 选择活动新闻通告
  
  新闻通告讨论区
选择节合理函数分析

折叠展开
合理函数分析
Introduction
::导言

The word asymptote is derived from the Greek word asymptotos, which translates to "not falling together. "
::单点字来自希腊语的单点字, 翻译为“ 不是一起坠落 ” 。

It was coined around the 3rd century B.C. by Greek mathematician Apollonius of Perga (above) in his work on conic sections, when he discovered lines that approached but did not intersect the curves he was studying.
::希腊数学家Perga(以上)的阿波罗尼乌斯于公元前三世纪左右在他的关于二次曲线的作品中发明了这一模型,当时他发现了接近但未交叉他正在研究的曲线的线条。

Removable Discontinuity
::无法移动的连续状态

Rational functions are defined as $\begin{aligned} r (x) = \frac{p (x)}{q (x)}, \end{aligned}$ where $\begin{aligned} p (x) \end{aligned}$ and $\begin{aligned} q (x) \end{aligned}$ are .
::有理函数定义为 r( x) = p( x)q( x) , p( x) 和 q( x) 是。

The end behavior of a rational function can often be identified by the horizontal or . That is, as the values of $\begin{aligned} x \end{aligned}$ get very large or very small, the graph of the rational function will approach the horizontal or oblique asymptote. Some rational functions have discontinuities, either instead of or along with any vertical asymptote . T hese are often characterized as removable discontinuities or holes.
::理性函数的结束行为通常可以通过水平或。也就是说, 当 x 的值变得非常大或非常小时, 理性函数的图将接近水平或斜线无症状。有些理性函数不连续, 而不是垂直无症状, 或者与任何垂直无症状相伴。这些功能通常被描述为可移动的不连续或孔。

Removable Discontinuity (or hole)
::可移动的禁用 (或孔)

A point where a function is discontinuous or undefined .

To determine the location of a hole on the graph of a rational function:
::要确定合理函数图形上的洞的位置 :

Step 1: Determine all of the factors of the polynomials in the numerator and the denominator of the given rational function.
::第1步:确定分子中多数值的所有因素和给定理性函数的分母。

Step 2: Determine any sets of common factors in the numerator and denominator. At this particular $\begin{aligned} x \end{aligned}$ -value, the common factors would create the undefined fraction $\begin{aligned} \frac{0}{0} \end{aligned}$ . Instead, these common factors should be canceled.
::第2步:确定分子和分母中的任何一组共同系数。在这一特定的X值上,这些共同系数将产生未定义的分数00。相反,这些共同系数应取消。

Step 3: Set each canceled factor equal to zero and solve for $\begin{aligned} x \end{aligned}$ . The result is the point(s) where the function is undefined, creating one or more points of discontinuity .
::第3步:设定每个取消系数等于零,并解决 x。结果就是函数未定义的点,从而产生一个或多个不连续点。



A rational function may have a vertical , a horizontal, and/or an oblique asymptote. A vertical asymptote is found by setting the denominator of a rational function in reduced form equal to zero and solving for $\begin{aligned} x \end{aligned}$ . A horizontal asymptote is found by creating a fraction with the leading terms of the numerator and denominator, and comparing the degrees. If the degree of the numerator is smaller than the degree of the denominator, then the horizontal asymptote equals $\begin{aligned} y = 0 \end{aligned}$ . If the degree of the numerator and denominator are the same, then the horizontal asymptote equals the ratio of the leading coefficients. If the degree of the numerator is larger than the degree of the denominator, then there is no horizontal asymptote. If the degree of the numerator is 1 greater than the degree of the denominator, rewrite the function by using long division to reveal the oblique asymptote.
::理性函数可能具有垂直、水平和/ 或斜度等同状态。通过为 x 设定减为零和溶解的理性函数分母, 发现垂直的静态。通过创建带有分子和分母主要条件的分母, 并比较度, 发现水平的静态。如果分子的程度小于分母的程度, 则水平的静态等于 y=0。如果分子和分母的程度相同, 则水平的静态等于主要系数的比率。如果分子的分母比分母的分母大, 那么没有水平的静态。如果分子的分母比分母的分母大, 则没有水平的静态。如果分子的分母比分母的分母大1, 则使用长的分法来重写函数。



Examples
::实例

Example 1
::例1

Consider the following rational function: $\begin{aligned} \frac{x^{2} + 2 x - 35}{x + 7} \end{aligned}$ . Find all restrictions on the domain and any vertical asymptotes.
::考虑以下合理函数 : x2+2x-35x+7 。查找对域和任何垂直单位数的所有限制。

Solution:
::解决方案 :

Step 1: Factor the numerator and reduce:
::第1步:乘以点数并减少:

$\begin{aligned} f (x) & = \frac{(x - 5) (x + 7)}{x + 7} \\ f (x) & = \frac{(x - 5) (x + 7)}{x + 7} . \end{aligned}$

:x) = (x- 5)(x+7) x+7f(x) = (x- 5)(x+7) x+7。

Step 2: There is no vertical asymptote for this function, but rather a hole in the graph at $\begin{aligned} x = - 7 \end{aligned}$ , so the domain is the set of all real numbers except $\begin{aligned} x = - 7 \end{aligned}$ .
::第2步:此函数没有垂直空点,而是在 x7 的图形中有一个洞,因此域是除 x7 外所有实际数字的集合。

Example 2
::例2

Find the restrictions on the domain and any asymptotes for the function:
::查找对域的限制和函数的元素:

$\begin{aligned} h (x) = \frac{3 x}{x^{2} - 25} \end{aligned}$

::h(x)=3x22-2-2-25

Solution:
::解决方案 :

Step 1: Set the denominator equal to 0:
::第1步:设定分母等于 0:

$\begin{aligned} x^{2} - 25 & = 0 \\ x^{2} & = 25 \\ x & = \pm 5 \end{aligned}$

::x2 - 25=0x2=25x% 5

Step 2: T he domain of $\begin{aligned} h (x) \end{aligned}$ is the set all real numbers $\begin{aligned} x \end{aligned}$ with the restriction $\begin{aligned} x \neq \pm 5 \end{aligned}$ . Since these values don't make the numerator equal to zero, $\begin{aligned} h (x) \end{aligned}$ has two vertical asymptotes, one at $\begin{aligned} x = 5 \end{aligned}$ and one at $\begin{aligned} x = - 5 \end{aligned}$ .
::第2步:h(x)的域是设定所有真实数字 x 的设置,并有限制 x @ @ @% 5 。由于这些值不能使分子为零, h(x) 有2个垂直小数, 1个在 x=5 , 1个在 x% 5 。

Step 3: Since the degree of the numerator is smaller than the degree of the denominator, the horizontal asymptote is at $\begin{aligned} y = 0 \end{aligned}$ .
::第3步:由于分子的分量小于分母的分母的分量,水平分数为y=0。

Example 3
::例3

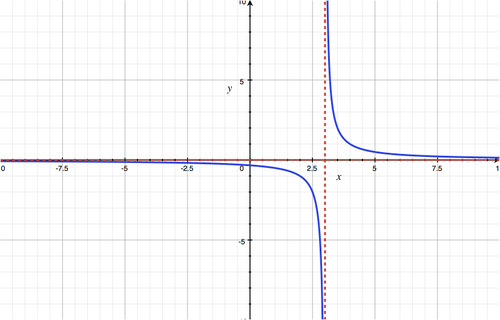
Graph $\begin{aligned} f (x) = \frac{1}{x - 3} \end{aligned}$ on the window [-10,10] by [-10,10], using online graphing software or a calculator.
::图f(x)=1x-3 在窗口[-10,10] [-10,10] 之前使用在线图形化软件或计算器在窗口[-10,10]上。

Solution:
::解决方案 :

When graphing a rational function by entering the function in the $\begin{aligned} Y = \end{aligned}$ screen, remember that you need to use " data-term="Parentheses" role="term" tabindex="0"> parentheses to group the numerator and denominator of the rational function.
::当通过输入 Y= 屏幕中的函数来绘制一个理性函数时,请记住,您需要使用括号来组合理性函数的分子和分母。

Vertical asymptotes are sometimes graphed as vertical lines.
::垂直的微粒有时被用垂直线划为垂直线。

Graphs of rational functions can be difficult to interpret if the window settings are not chosen carefully.
::如果不仔细选择窗口设置, 则很难解释合理函数的图形。

$\begin{aligned} y = \frac{1}{x - 3} \end{aligned}$ showing vertical line at $\begin{aligned} x = 3 \end{aligned}$ .
::y=1x-3 在 x=3 显示垂直线条。

Note that $\begin{aligned} f (x) \end{aligned}$ is undefined and has a vertical asymptote at $\begin{aligned} x = 3 \end{aligned}$ , but some graphing calculators draw the graph with a vertical line at $\begin{aligned} x = 3 \end{aligned}$ . One way to “fix” this problem is to press MODE and select the option “Dot” rather than “Connected.”
::请注意 f( x) 未定义, 且在 x=3 上有一个垂直空位, 但有些图形计算器在 x= 3 上用垂直线绘制图形。 “ 固定 ” 的方法之一是按 MODE 键, 选择“ 点 ” 选项而不是“ 连接 ” 。

Example 4
::例4

What are the asymptotes of the function below?
::下面函数的微数是多少 ?

$\begin{aligned} k (x) = \frac{x^{2}}{x^{2} + 5} \end{aligned}$

:xx) =x2x2+5

Solution:
::解决方案 :

Set the denominator equal to zero:
::设定分母为零 :

$\begin{aligned} x^{2} + 5 & = 0 \\ x^{2} & = - 5 \end{aligned}$

::x2+5=0x2=%5

There are no real solutions, so there are no vertical asymptotes. There is a horizontal asymptote at $\begin{aligned} x = 1 \end{aligned}$ .
::没有真实的解决方案, 所以没有垂直的静态。 x=1 上有一个水平的静态。

Example 5
::例5

Find the vertical asymptotes of
::查找垂直的单位数

$\begin{aligned} g (x) = \frac{x^{3}}{x^{2} + 1} . \end{aligned}$

::g(x) =x3x2+1。

Solution:
::解决方案 :

Set the denominator equal to zero:
::设定分母为零 :

$\begin{aligned} x^{2} + 1 & = 0 \\ x^{2} & = - 1 \\ x & = \pm \sqrt{- 1} . \end{aligned}$
There are no real solutions, so there are no vertical asymptotes and no restrictions on the domain of this function.
::x2+1=0x21x1. 不存在真正的解决方案, 因此没有垂直的单位数, 也没有限制此函数的域。

Example 6
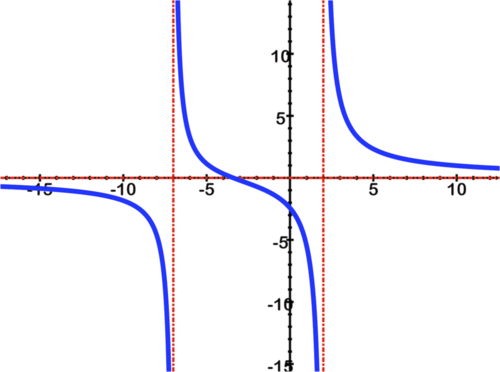
::例6

Graph the function and find any asymptotes using technology: $\begin{aligned} f (x) = \frac{6}{x - 2} + \frac{4}{x + 7} \end{aligned}$
::图形函数和查找任何使用技术的 asymptotes: f( x)=6x- 2+4x+7

Solution:
::解决方案 :

Using online graphing software or a graphing calculator, type the given equation . The graph should look like:
::使用在线图形化软件或图形化计算器,键入给定方程式。该图形应看起来像 :

There are asymptotes at $\begin{aligned} x = 2 \end{aligned}$ and $\begin{aligned} x = - 7 \end{aligned}$ and $\begin{aligned} y = 0 \end{aligned}$ .
::在 x=2 和 x=7 和 y=0 处有小数点。

Example 7
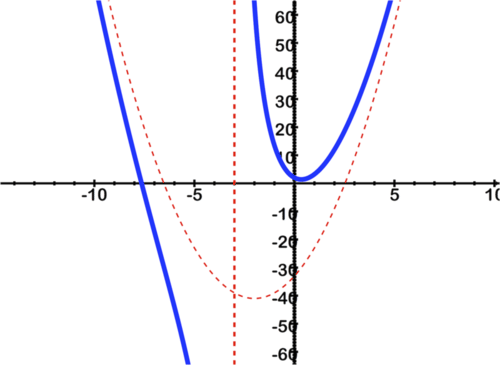
::例7

Using technology, find all intercepts , asymptotes, and removable discontinuities, and graph: $\begin{aligned} \frac{2 x^{3} + 14 x^{2} - 9 x + 6}{x + 3} . \end{aligned}$
::使用技术,找到所有拦截、无症状和可移动的不连续状态,图表:2x3+14x2-9x+6x+3。

Solution:
::解决方案 :

The graph should look like the one below. The intercepts are at (approximately) $\begin{aligned} (- 7.64, 0) \end{aligned}$ and (exactly) $\begin{aligned} (0, 2) \end{aligned}$ . There is a vertical asymptote at $\begin{aligned} x = - 3 \end{aligned}$ . There are no , but if you divided the numerator by the denominator , a curved asymptote can be found : $\begin{aligned} y = 2 x^{2} + 8 x - 33 \end{aligned}$ .
::图形应该像下面的图形。截取器在( 约) (- 7. 64, 0) 和( 确切) ( 0, 2) 处。 x\\\ 3 处有一个垂直的空位。没有。但是, 如果您用分母将分子除以分子, 则可以找到一个曲线的空位 : y= 2x2+8x- 33 。

Example 8
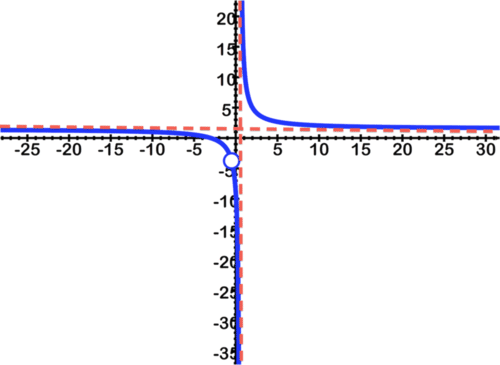
::例8

Find any removable discontinuities and graph $\begin{aligned} \frac{6 x^{2} + 21 x + 9}{4 x^{2} - 1} \end{aligned}$ .
::查找任何可移动的不连续状态和图 6x2+21x+94x2-1。

Solution:
::解决方案 :

Step 1: The function simplifies to
$\begin{aligned} \frac{3 (2 x^{2} + 7 x + 3)}{4 (x^{2} - \frac{1}{4})} \to \frac{3 (2 x + 1) (x + 3)}{4 (x - \frac{1}{2}) (x + \frac{1}{2})} . \end{aligned}$

::第1步:该功能简化为3(2x2+7x+3)4(x2-14)3(2x+1)(x+3)4(x-12)(x+12)。

Note that the factors $\begin{aligned} 2 x + 1 \end{aligned}$ and $\begin{aligned} x + \frac{1}{2} \end{aligned}$ indicate the same common factor . Alternatively, you could have factored this to make this more evident:
::注意因数 2x+1 和 x+12 表示相同的共同因数。或者,您可以将这一因数乘以使这一点更加明显:

$\begin{aligned} \frac{3 (2 x^{2} + 7 x + 3)}{4 x^{2} - 1} \to \frac{3 (2 x + 1) (x + 3)}{(2 x - 1) (2 x + 1)} . \end{aligned}$

::3(2x2+7x+3)、4x2-13(2x+1)(x+3)(2x-1)(2x+1)。

Since the factor cancels, there is a hole at $\begin{aligned} x = - \frac{1}{2} \end{aligned}$ . The other factor in the denominator, which does not cancel, means that there is a vertical asymptote at $\begin{aligned} x = \frac{1}{2} \end{aligned}$ .
::自因子取消后, x\\\\12 处有一个洞。分母中另一个不取消的因子意味着 x=12 处有一个垂直的空位。

Step 2: There is a horizontal asymptote at $\begin{aligned} y = \frac{3}{2} \end{aligned}$ since the degree of the numerator and denominator are equal.
::第2步:y=32有一个水平同位数,因为分子和分母的程度相等。

Step 3: The intercepts are $\begin{aligned} (- 3, 0) \end{aligned}$ and $\begin{aligned} (0, - 9) \end{aligned}$ , which you can find by setting the numerator (after cancelling the matching factor) to 0 and by plugging in 0 and evaluating the function.
::第3步:拦截是(-3,0)和(0,-9),您可以通过将分子(在取消匹配系数后)设置为0和插入0并评价函数来找到。

Step 4: The graph should look like:
::第4步:图表应看起来像:

Summary
::摘要

Rational functions have two types of discontinuities:

Infinite—at vertical asymptotes
::无限- 垂直无状

Removable—factors that cancel
::可移除 - 取消取消的驱动因素

::理性功能有两种不连续性类型:无限-在垂直无音量-可移动性-取消的因素。

When using technology, asymptotes can be obscured. Algebraic techniques help to identify the asymptotes.
::当使用技术时,可以隐蔽微粒。代数技术有助于识别微粒。

Review
::回顾

For problems 1-5, factor the numerator and denominator, then set the denominator equal to zero and solve to find restrictions on the domain:
::对于问题1至5,乘以分子和分母,然后将分母设为零,然后解决以找出对域的限制:

$\begin{aligned} y = \frac{x^{2} + 3 x - 10}{x - 2} \end{aligned}$
::y=x2+3x-10x-2

$\begin{aligned} f (x) = \frac{x^{2} + 2 x - 24}{x - 4} \end{aligned}$
:xx) =x2+2x-24x-4

$\begin{aligned} f (x) = \frac{x^{2} - 12 x + 32}{x - 4} \end{aligned}$
:xx) =x2 - 12x+32x- 4

$\begin{aligned} y = \frac{x^{2} + \frac{21}{20}}{x + \frac{4}{5}} \end{aligned}$
::y=x2+2120x+45

$\begin{aligned} y = \frac{x^{2} + 13 x + 42}{x + 7} \end{aligned}$
::y=x2+13x+42x+7

For each problem below, input the function into your graphing software or calculator carefully and accurately. Record any asymptotes or holes and record x and y intercepts. Finally, either copy and print or sketch the image of the graphed function.
::对于下面的每一个问题, 请仔细准确地将函数输入您的图形化软件或计算器。记录任何小孔或孔, 记录 x 和 y 拦截。最后, 复制和打印或绘制图形化函数的图像。

$\begin{aligned} y = \frac{x^{3} + 5 x^{2} + 3 x + 7}{x - 1} \end{aligned}$
::y=x3+5x2+3x+7x-1

$\begin{aligned} y = \frac{9 x^{2} + 6}{x} \end{aligned}$
::y= 9x2+6x y= 9x2+6x

$\begin{aligned} f (x) = \frac{x - 7}{2 x^{2} - 11 x - 21} \end{aligned}$
:xx) =x-72x2-11x-21

$\begin{aligned} f (x) = \frac{5 x^{3} - 9 x^{2} - 7 x + 1}{x^{2} - 4} \end{aligned}$
:x)=5x3-9x2-7x+1x2-4)

$\begin{aligned} y = \frac{x^{2} + x - 30}{x + 6} \end{aligned}$
::y=x2+x-30x+6 y=x2+x-30x+6

$\begin{aligned} y = \frac{4 x^{3} + 2 x^{2} + 7}{(x + 2)^{2}} \end{aligned}$
::y=4x3+2x2+7(x+2)2

$\begin{aligned} f (x) = \frac{x^{3} - 2 x^{2} - 3 x}{x^{2} - 5 x + 6} \end{aligned}$
:x) =x3-2x2-3x2-3x2-5x6

$\begin{aligned} f (x) = \frac{- 6 x^{3} + 8 x^{2} + 7}{x^{2}} \end{aligned}$
:x) 6x3+8x2+7x2

$\begin{aligned} y = \frac{- 5 x^{2} - 2 x - 5}{x^{2} + 2} \end{aligned}$
::y5x2 - 2x - 5x2+2

$\begin{aligned} y = \frac{x - 1}{x^{3} - 2} \end{aligned}$
::y=x - 1x3 - 2

Answers for Review
::供审查的答复

Please see the Appendix.
::请参看附录。

Resources
::资源

章节大纲

常规

合理函数分析

Introduction ::导言

Removable Discontinuity ::无法移动的连续状态

Removable Discontinuity (or hole) ::可移动的 禁用 (或孔)

To determine the location of a hole on the graph of a rational function: ::要确定合理函数图形上的洞的位置 :

Examples ::实例

Example 7 ::例7

Example 8 ::例8

Summary ::摘要

Review ::回顾

Answers for Review ::供审查的答复

Resources ::资源

Introduction
::导言

Removable Discontinuity
::无法移动的连续状态

Removable Discontinuity (or hole)
::可移动的禁用 (或孔)

To determine the location of a hole on the graph of a rational function:
::要确定合理函数图形上的洞的位置 :

Examples
::实例

Example 7
::例7

Example 8
::例8

Summary
::摘要

Review
::回顾

Answers for Review
::供审查的答复

Resources
::资源