3.10 多元和理性不平等

Section outline

• Select section General

  Collapse Expand

  General

  Collapse all Expand all

  • Select activity 新闻通告

    

    新闻通告 Forum
• Select section 多元和理性不平等

  Collapse Expand

  多元和理性不平等

  播放段落

  Introduction
  ::导言

  

  播放段落

  A  manufacturer needs to determine how to cut squares from a rectangular piece of cardboard, which is 8 inches by 10 inches, to create an open box. The volume function is  

  $$\begin{align*}V(x)=x(10-2x)(8-2x)=4x^3-36x^2+80x,\end{align*}$$
  ::制造商需要确定如何将方形从纸板的长方形块(8英寸乘10英寸)中切除出来,以创建一个打开的框。音量函数为 V( x) =x( 10- 2x)( 8- 2x) =4x3- 36x2+80x,

  播放段落

  where $\begin{align*}x\end{align*}$  is the length of the side of the square.  
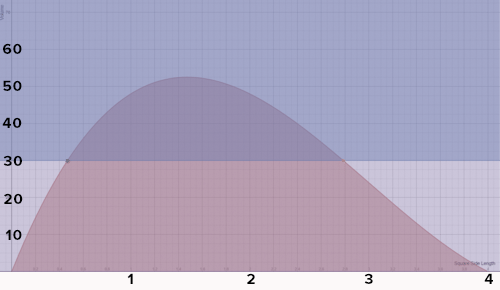
  ::x 是方形侧的长度。

  播放段落

  In another section, we discussed the problem of the volume of this box. Now the manufacturer is purchasing equipment to cut the squares from the cardboard. The mathematical task is to determine a range of values for the side of the square so that the volume is 30 cubic  inches or greater. The graph below shows the volume of the box as a function of its height,  and helps to visualize the question:
  ::在另一部分,我们讨论了这个框的体积问题。 现在制造商正在购买设备, 以便从纸板上切开方形。 数学的任务是确定方形侧的值范围, 使方形的体积达到或大于30立方英寸。 下图显示框的体积与其高度的函数, 有助于直观问题 :

  

  播放段落

  Although the graph helps to visualize the problem, algebraic methods help to identify solutions when they are not easily seen. The techniques to answer the question are below.
  ::虽然图有助于将问题直观化,但代数法有助于在不易看到时找出解决办法。 回答问题的方法如下。

  播放段落

  Quadratic Inequalities
  ::赤道不平等

  播放段落

  are inequalities that have one of the following forms:
  ::具有以下一种形式的不平等:

  播放段落

  $$\begin{align*}ax^{2}+bx+c>0\end{align*}$$
  ::ax2+bx+c>0

  播放段落

  or
  ::或

  播放段落

  $$\begin{align*}ax^{2}+bx+c<0.\end{align*}$$
  ::ax2+bx+c <0。

  播放段落

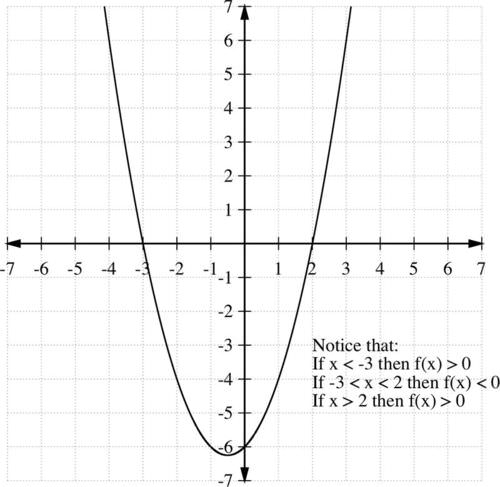
  These inequalities can be solved by extending the techniques to solve  quadratic equations. For example, consider the graph of the equation  $\begin{align*}y = x^2 + x - 6\end{align*}$ . 
  ::这些不平等可以通过扩大解决二次方程的技术来解决。例如,考虑y=x2+x-6的方程图。

  

  播放段落

  Notice that the curve intersects the $\begin{align*}x-\end{align*}$ axis at -3 and 2, since:
  ::注意曲线在 -3 和 2 处交叉 x - 轴, 原因是 :

  播放段落

  $$\begin{align*}x^{2}+x-6 = 0 \quad \\ (x+3)(x-2) = 0 \ \ \\ x + 3 = 0 \ \text{or} \ x-2 = 0\\ x = -3 \ \text{or} \ x = 2 \quad\end{align*}$$
  ::x2+x -6=0( x+3)( x- 2)=0 x3=0 3=0 或 x- 2=0x%3 或 x=2

  播放段落

  From graph, we notice the following:
  ::从图表中,我们注意到以下各点:

  播放段落
  • If $\begin{align*}x < -3\end{align*}$ then $\begin{align*}f(x)>0.\end{align*}$
    ::如果 x3 然后 f( x) > 0 。
  播放段落
  • If $\begin{align*}-3 < x <2\end{align*}$ , then $\begin{align*}f(x)<0.\end{align*}$
    ::如果 - 3 <x < 2, 那么f(x) < 0 。
  播放段落
  • If $\begin{align*}x > 2\end{align*}$ , then $\begin{align*}f(x)>0.\end{align*}$
    ::如果 x> 2, 那么 f( x) > 0 。

  播放段落

  Therefore , $\begin{align*}x^{2}+x-6>0\end{align*}$ whenever $\begin{align*}x<-3\end{align*}$ or $\begin{align*}x>2\end{align*}$ , and $\begin{align*}x^{2}+x-6<0\end{align*}$ when $\begin{align*}-3 < x < 2\end{align*}$ .
  ::因此,在 x2+x-6>0 和 x2+6 <0 和 3 <x < 2 时,均值为 x2+x-6>0。

  播放段落

  Solve Polynomial Inequalities
  ::解决多元不平等

  播放段落

  Solving polynomial inequalities is very similar to solving quadratic inequalities. The basic steps are the same:
  ::解决多元不平等与解决二次不平等非常相似。

  播放段落
  1. Set up the inequality in the form $\begin{align*}p(x)>0\end{align*}$ (or $\begin{align*}p(x)<0, p(x)\le0,p(x)\ge0\end{align*}$ ).
     ::设置 p( x) > 0 (或 p( x) < 0, p( x) =0, p( x) =0) 形式的不平等。
  播放段落
  2. Find the solutions to the equation $\begin{align*}p(x)=0\end{align*}$ .
     ::查找公式p(x)=0的解决方案。
  播放段落
  3. Divide the number line into intervals based on the solutions to $\begin{align*}p(x)=0\end{align*}$ .
     ::根据 p( x) =0 的解决方案将数字行除以间隔。
  播放段落
  4. Use test points to find solution sets to the equation.
     ::使用测试点来寻找方程式的解决方案集 。

  播放段落

  Solve Rational Inequalities
  ::解决理性不平等

  播放段落

  The method outlined above also works for solving inequalities involving rational functions . Recall that for rational functions, you can find the roots (or zeros) by setting the numerator equal to zero.
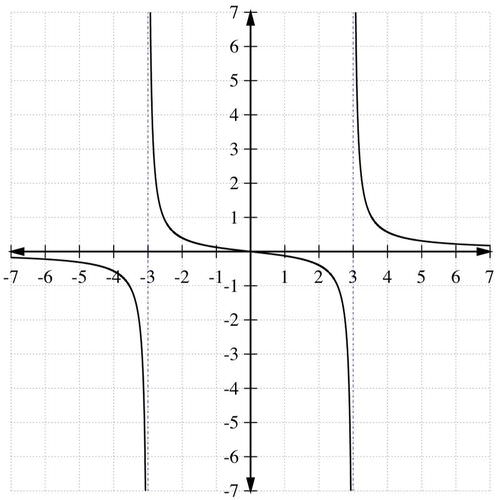
  ::上述方法还有助于解决涉及理性功能的不平等问题。回顾对于理性功能,您可以通过将分子数设为零来找到根(或零)。

  播放段落

  However, one step is added to the process of solving rational inequalities, because a rational function can also change signs at its vertical asymptotes or at a hole  in the graph. For instance, look at the graph of the function $\begin{align*}r(x)=\frac{x}{x^{2}-9}\end{align*}$ below:
  ::然而,在解决合理不平等的过程中又增加了一个步骤,因为理性功能也可以改变其垂直微粒或图中一个洞的标志。例如,看看下面的函数 r(x)=xx2-9的图示:

  

  播放段落

  To help  solve the inequality $\begin{align*}\frac{x}{x^{2}-9}>0\end{align*}$ , use the following p oints: $\begin{align*}x=0, x=3,\end{align*}$ and $\begin{align*}x=-3\end{align*}$ . $\begin{align*}x=0\end{align*}$ is the solution of setting the numerator equal to 0, which gives the only root of the function.    $\begin{align*}x=\pm3\end{align*}$ are the vertical asymptotes, since the se values are not in the domain of the  function .
  ::为帮助解决不平等问题xx2-9>0, 使用以下点: x=0, x=3, 和 x3. x=0 是将分子设置为 0 的解决方案, 这给出了函数的唯一根。 x3 是垂直的单数, 因为这些值不在函数的域内 。

  播放段落

  Using the graph or test points, we can build the table:
  ::使用图表或测试点,我们可以构建表格:

  Interval	Test Point	Positive/Negative?	Part of Solution set?
  $\begin{align*}(-\infty,-3)\end{align*}$	-4	-	no
  (-3, 0)	-2	+	yes
  (0, 3)	2	-	no
  $\begin{align*}(3,+\infty)\end{align*}$	4	+	yes

  播放段落

  Thus, the solutions to $\begin{align*}\frac{x}{x^{2}-9}>0\end{align*}$ are $\begin{align*}(-3,0)\cup(3,+\infty)\end{align*}$ .
  ::因此,xx2-9>0的解决方案是(-3,0)(3, )。

  播放段落

  Examples
  ::实例

  播放段落

  Example 1
  ::例1

  播放段落

  What is the solution set of the inequality $\begin{align*}2x^{2}+7x-4<0\end{align*}$ ?
  ::不平等2x2+7x-4<0的解决方案是什么?

  播放段落

  Solution:
  ::解决方案 :

  播放段落

  Step 1 : One option is to  graph the function $\begin{align*}f(x)=2x^{2}+7x-4\end{align*}$ and look for the the values of $\begin{align*}x\end{align*}$ such that the inequality $\begin{align*}f(x)<0\end{align*}$ is true.
  ::第1步:一个选项是绘制函数f(x)=2x2+7x-4的图形,并寻找 x 的值,使不平等 f(x) <0 真实。

  

  播放段落

  Step 2: From graph, $\begin{align*}2x^{2}+7x-4<0\end{align*}$ only if
  ::步骤 2: 从图图中, 仅在下列条件下 2x2+7x-4<0 2x2+7x-4<0

  播放段落

  $$\begin{align*}-4 < x < \frac{1}{2}.\end{align*}$$
  ::- 4 <x < 12.

  播放段落

  Step 3: So the solution set is $\begin{align*}x\in\left ( -4,\frac{1}{2} \right )\end{align*}$ or, in set builder notation, $\begin{align*}\left \{x|-4 < x < \frac{1}{2} \right \}\end{align*}$ .
  ::第3步:因此,解决方案集是 x(- 4, 4, 12),或者,在设定构建符符号中, {x4 < x < 12} 。

  播放段落

  Although the method of graphing to find the solution set of an inequality is easy to follow, an algebraic method also can be used. The algebraic method involves finding the $\begin{align*}x-\end{align*}$ intercepts of the graph and then dividing the $\begin{align*}x-\end{align*}$ axis into intervals separated by the $\begin{align*}x-\end{align*}$ intercepts. The example below illustrates this method.
  ::虽然找到不平等的一套解决办法的图表方法很容易遵循,但也可以使用代数法。代数法涉及查找图形的x-截面,然后将x-轴分割成由x-截面隔开的间隔。下面的例子说明了这一方法。

  播放段落

  Example 2
  ::例2

  播放段落

  Find the solution set of the quadratic inequality $\begin{align*}x^{2}+2x-8>0\end{align*}$ .
  ::寻找二次不平等 x2+2x-8>0 的解决方案集 。

  播放段落

  Solution:
  ::解决方案 :

  播放段落

  Step 1:  S olve
  ::步骤1:解决

  播放段落

  $$\begin{align*}x^{2}+2x-8 & = 0\\ (x+4)(x-2) & = 0.\end{align*}$$
  ::x2+2x-8=0(x+4)(x-2)=0。

  播放段落

  The two solutions to this quadratic equation are $\begin{align*}x=-4\end{align*}$ and $\begin{align*}x=2\end{align*}$ . Thus, the zeros of the function $\begin{align*}f(x)=x^{2}+2x-8\end{align*}$ are -4 and 2.
  ::此二次方程式的两个解决方案是 x4 和 x=2 。 因此,函数 f( x) = x2+2x-8 的零是 - 4 和 2 。

  播放段落

  Step 3: These points divide the $\begin{align*}x-\end{align*}$ axis into three intervals: $\begin{align*}(-\infty,-4), (-4,2),\end{align*}$ and $\begin{align*}(2,\infty)\end{align*}$ . Choose a test point from each interval and substitute it into $\begin{align*}f(x)\end{align*}$   to determine its sign  (negative or positive). This procedure can be simplified by making the table shown below.
  ::步骤3:这些点将x-轴分为三个间隔,-4,(-4),(-2,2)和(2,)。从每个间隔选择一个试验点,将其改为f(x),以确定其符号(负或正)。

  Interval	Test Point	$\begin{align*}x^{2}+2x-8\end{align*}$ Positive/Negative?	Part of Solution set?
  $\begin{align*}(-\infty,-4)\end{align*}$	-5	+	yes
  (-4, 2)	1	-	no
  $\begin{align*}(2,+\infty)\end{align*}$	3	+	yes

  播放段落

  From the table, it is clear that  $\begin{align*}x^{2}+2x-8>0\end{align*}$ if and only if $\begin{align*}x<-4\end{align*}$  or  $\begin{align*}x>2\end{align*}$ . The solution set can also be written as
  ::从表格中可以清楚地看出,如果且只有在 x4 或 x>2 的情况下, x2+2x-8_8>0 x2+2x-8>0。

  $$\begin{align*}(-\infty,-4)\cup(2,+\infty).\end{align*}$$

  播放段落

  Example 3
  ::例3

  

  播放段落

  A pool  has a length 10 meters more than twice the width. Find the possible widths such that the area of the surface of the  pool  cannot exceed 100 square meters.
  ::游泳池的长度为10米,宽度是宽度的两倍以上。 找出可能的宽度, 以便游泳池表面的面积不能超过100平方米。

  播放段落

  Solution:
  ::解决方案 :

  播放段落

  Step 1:  Let $\begin{align*}W\end{align*}$ be the width of the pool  and $\begin{align*}L\end{align*}$ its length. Thus,
  ::第一步:让W成为池的宽度和L的长度。因此,

  播放段落

  $$\begin{align*}L = 10+2W.\end{align*}$$
  ::L=10+2W。

  播放段落

  Step 2: The surface area of a pool  is
  ::第2步:池的表面积为

  播放段落

  $$\begin{align*}A & = LW\\ & = (10+2W)(W)\\ & = 10W +2W^2.\end{align*}$$
  ::A=LW=(10+2W)(W)=10W+2W2。

  播放段落

  Step 3: The area cannot exceed $\begin{align*}100 \ m^{2}\end{align*}$ . So
  ::第3步:面积不得超过100平方米。

  播放段落

  $$\begin{align*}10W+2W^{2} \leq 100.\end{align*}$$
  ::10W+2W21100。

  播放段落

  Step 4: Solve for 0:
  ::步骤4:解决0:

  播放段落

  $$\begin{align*}2W^{2}+10W-100 \leq 0.\end{align*}$$
  ::2W2+10W-10000。

  播放段落

  Step 3: Divide both sides by 2:
  ::第3步:将双方除以2:

  播放段落

  $$\begin{align*}W^{2}+5W-50 \leq 0.\end{align*}$$
  ::W2+5W-5000。

  播放段落

  Step 4: Determine the roots for $\begin{align*}W^{2}+5W-50=0\end{align*}$ ,
  ::步骤4:确定W2+5W-50=0的根根根;

  播放段落

  $$\begin{align*}W^{2}+5W-50=(W+10)(W-5).\end{align*}$$
  ::W2+5W-50=(W+10)(W-5)。

  播放段落

  Step 5: The partition points are 5 and -10, which form three intervals. Since the width must be positive, ignore -10. So there are only two intervals to consider, (0, 5] and [ 5, ∞ ) . 
  ::第5步:分区点为5和 - 10, 间隔为3个。 由于宽度必须是正的, 忽略 - 10 。 所以只有两个间隔需要考虑, (0, 5) 和 [5, *] 。

  播放段落

  The maximal allowable area is  $\begin{align*}100 \ m^{2}\end{align*}$  .  By testing points, you can find that the width must be $\begin{align*}0 < W \leq 5\end{align*}$ .
  ::最大允许区域为 100 平方米。通过测试点,您可以发现宽度必须是 0<W}5 。

  播放段落

  Example 4
  ::例4

  播放段落

  Solve $\begin{align*}x^{3}-3x^{2}+2x\ge0.\end{align*}$
  ::解决 x3 - 3x2+2x%0 。

  播放段落

  Solution:
  ::解决方案 :

  播放段落

  S tep 1:

  $$\begin{align*}x^{3}-3x^{2}+2x & = 0\\ x(x^2-3x+2) & = 0\\ x(x-2)(x-1) & = 0\end{align*}$$
  ::1:x3-3x2+2x=0x(x2-3x+2)=0x(x-2)(x-1)=0

  播放段落

  Step 2: The zeros are at $\begin{align*}x=0, \ x=1,\end{align*}$ and $\begin{align*}x=2\end{align*}$ .
  ::第2步:零为 x=0, x=1, 和 x=2。

  播放段落

  Step 3:
  ::第3步:

  Interval	Test Point	Positive/Negative?	Part of Solution set?
  $\begin{align*}(-\infty, 0)\end{align*}$	-5	-	no
  (0, 1)	$\begin{align*}\frac{1}{2}\end{align*}$	+	yes
  (1, 2)	$\begin{align*}\frac{3}{2}\end{align*}$	-	no
  $\begin{align*}(2,+\infty)\end{align*}$	3	+	yes

  播放段落

  Notice that this inequality is greater than or equal to zero, so we include the zeros in the solution set. Therefore, the solutions are $\begin{align*}[0,1]\cup[2,\infty)\end{align*}$ .
  ::请注意,这种不平等大于或等于零,因此,我们把零点包括在设定的解决方案中。因此,解决方案是[01][2,]。

  播放段落

  Example 5
  ::例5

  播放段落

  Solve $\begin{align*}6x^{4}+5x^{2}<25\end{align*}$ .
  ::解决 6x4+5x2<25。

  播放段落

  Solution:
  ::解决方案 :

  播放段落

  Step 1:  Rewrite  the inequality to $\begin{align*}6x^{4}+5x^{2}-25<0\end{align*}$ .
  ::步骤1:将不平等重写为 6x4+5x2-25<0。

  播放段落

  Step 2: Solve the equation $\begin{align*}6x^{4}+5x^{2}-25=0\end{align*}$ .
  ::步骤2:解决6x4+5x2-25=0等式。

  播放段落

  $$\begin{align*}6x^{4}+5x^{2}-25 & = 0\\ (3x^2-5)(2x^2+5) & = 0\end{align*}$$
  ::6x4+5x2-25=0(3x2-5)(2x2+5)=0

  播放段落

  Step 3: The 1st factor yields the solutions $\begin{align*}x=\pm\sqrt{\frac{5}{3}},\end{align*}$ and there are no real solutions for the 2nd factor.
  ::第3步:第1因数产生解决方案 x53,第2因数没有真正的解决方案。

  Interval	Test Point	Positive/Negative?	Part of Solution set?
  $\begin{align*}\left ( -\infty,-\sqrt{\frac{5}{3}} \right )\end{align*}$	-3	+	no
  $\begin{align*}\left ( -\sqrt{\frac{5}{3}},\sqrt{\frac{5}{3}} \right )\end{align*}$	0	-	yes
  $\begin{align*}\left ( \sqrt{\frac{5}{3}},+\infty \right )\end{align*}$	3	+	no

  播放段落

  Finally, the solution set is $\begin{align*}\left ( -\sqrt{\frac{5}{3}},\sqrt{\frac{5}{3}} \right )\end{align*}$ .
  ::最后,一套解决办法是(第53章,第53章)。

   

  播放段落

  Example 6
  ::例6

  播放段落

  Find the solution set of the inequality
  ::寻找不平等的一套解决办法

  播放段落

  $$\begin{align*}\frac{4x-12}{3x-2}<0.\end{align*}$$
  ::4-123x-2<0。

  播放段落

  Solution:
  ::解决方案 :

  播放段落

  Step 1: From the numerator, we solve $\begin{align*}4x-12=0\end{align*}$ or $\begin{align*}x=3\end{align*}$ . In the denominator, solve $\begin{align*}3x-2=0,\end{align*}$ and we find the critical point $\begin{align*}x=\frac{2}{3}\end{align*}$ .
  ::第1步:从分子中,我们破解 4x-12=0 或 x=3。 在分母中,解3x-2=0,我们找到关键点 x=23。

  播放段落

  Step 2: Mak e the table:
  ::第2步:使表格:

  Interval	Test Point	Positive/Negative?	Part of Solution set?
  $\begin{align*}\left ( -\infty,\frac{2}{3} \right )\end{align*}$	0	+	no
  $\begin{align*}\left ( \frac{2}{3},3 \right )\end{align*}$	1	-	yes
  $\begin{align*}(3,+\infty)\end{align*}$	5	+	no

  播放段落

  Step 3: Therefore, the solution set includes the numbers in the interval $\begin{align*}\left ( \frac{2}{3},3 \right )\end{align*}$ . Or in set-builder notation, the solution is $\begin{align*}\left \{ x|\frac{2}{3} < x < 3 \right \}\end{align*}$ .
  ::第3步:因此,所设定的解决方案包括间隔(23,3)中的数字,或者在固定建筑工符号中,解决方案是{x23 <x<3}。

  播放段落

  Example 7
  ::例7

  播放段落

  Solve the inequality $\begin{align*}\frac{3x+2}{x^{2}}>3.\end{align*}$
  ::解决3x+2x2>3的不平等。

  播放段落

  Solution:
  ::解决方案 :

  播放段落

  Step 1: R ewrite the inequality to get zero on one side:
  ::第一步:重写不平等,一面为零:

  播放段落

  $$\begin{align*}\frac{3x+2}{x^{2}} & > 3\\ \frac{3x+2}{x^{2}} - 3 & > 0\\ \frac{-3x^2+3x+2}{x^{2}} & > 0\\ \frac{3x^2-3x-2}{x^{2}} & < 0\end{align*}$$
  ::3x+2x2>33x+2x2_3>0-3x2+3x2+2x2>03x2_3x-2x2<0

  播放段落

  Notice in the last step, both sides were multiplied by -1, so the direction of the inequality changed.
  ::最后一步的警告是,双方乘以-1,因此不平等的方向改变了。

  播放段落

  Step 2: The numerator cannot be factored, so use the quadratic formula to solve $\begin{align*}3x^{2}-3x-2=0\end{align*}$ .
  ::第2步:无法计算分子,所以使用二次公式解析 3x2-3x-2=0。

  播放段落

  $$\begin{align*}x & = \frac{ 3 \pm \sqrt{9-4(3)(-2)}}{6}\\ x & = \frac{3 \pm \sqrt{33}}{6}\end{align*}$$
  ::x=3=9-4(3)(-2-2)6x=3336

  播放段落

  Step 3: So the two zeros of the rational function are $\begin{align*}x=\frac{3+\sqrt{33}}{6}\approx 1.457\end{align*}$ and $\begin{align*}x=\frac{3-\sqrt{33}}{6}\approx-0.457\end{align*}$ . Be careful to remember the point at  $\begin{align*}x=0\end{align*}$  due to the $\begin{align*}x^{2}\end{align*}$  factor in the denominator of the rational expression . Using these values, construct the table:
  ::步骤 3 : 所以理性函数的两个零是 x= 33361.361.457 和 x= 333333. 0. 457. 注意记住x=0的点, 原因是合理表达式分母中的 x2 系数。 使用这些值构建表格 :

  Interval	Test Point	Is  $\begin{align*}\frac{3x^2-3x-2}{x^2}\end{align*}$   Positive/Negative?	Part of Solution set?
  $\begin{align*}\left ( -\infty,\frac{3-\sqrt{33}}{6} \right )\end{align*}$	-1	+	no
  $\begin{align*}\left ( \frac{3-\sqrt{33}}{6},0 \right )\end{align*}$	$\begin{align*}-\frac{1}{4}\end{align*}$	-	yes
  $\begin{align*}\left ( 0,\frac{3+\sqrt{33}}{6} \right )\end{align*}$	1	-	yes
  $\begin{align*}\left ( \frac{3+\sqrt{33}}{6},+\infty \right )\end{align*}$	2	+	no

  播放段落

  The final solution set is $\begin{align*}\left ( \frac{3-\sqrt{33}}{6},0 \right )\cup\left ( 0,\frac{3+\sqrt{33}}{6} \right ).\end{align*}$
  ::最后的解决方案是 (3336,0) (0.3336)。

  播放段落

  Notice that  at $\begin{align*}x=0\end{align*}$ ,  the rational function is undefined , so 0 cannot satisfy the inequality.
  ::注意在 x=0 时, 理性函数未定义, 所以 0 无法满足不平等 。

  播放段落

  Example 8
  ::例8

  播放段落

  The McNeil Surf Company makes wetsuits. For a given number of wetsuits $\begin{align*}x\end{align*}$ , McNeil's profit, in dollars, is given by the function $\begin{align*}P(x)=-0.01x^{2}+25x-3000\end{align*}$ .
  ::McNeil Surf公司制造湿衣服。对于一定数量的湿衣服 x,McNeil的利润(美元)由函数P(x)0.01x2+25x-3000提供。

  播放段落

  a) If the manager of McNeil wants the profit to stay above $9,000, what is the minimum and maximum number of wetsuits the company can manufacture to maintain that level of profit?
  :a) 如果McNeil的经理希望利润保持在9 000美元以上,那么公司为保持这一利润水平而制造的湿衣的最低和最高数量是多少?

  播放段落

  Solution:
  ::解决方案 :

   

  播放段落

  Set up the inequality:
  ::建立不平等:

  播放段落

  $$\begin{align*}-0.01x^{2}+25x-3000 & > 9000\\ -0.01x^2 + 25x -12000 & > 0.\end{align*}$$
  ::- 0.01x2+25x-3000>900-0.01x2+25-12000>0。

  播放段落

  With a calculator, graph the function $\begin{align*}Y_{1}=-0.01x^{2}+25x-12000\end{align*}$ . Set the   WINDOW:
  ::用计算器绘制函数 Y1\\ 0.01x2+25x- 2000。 设置 WINDOW :

  播放段落

  $\begin{align*}Xmin = -1000, Xmax = 4000, Xscl = 500, Ymin=-5000, Ymax=5000, Yscl=1000 \ xres=1\end{align*}$
  ::Xmin1000,Xmax=400,Xscl=500,Ymin500,Ymax=500,Yscl=1000 xres=1

  播放段落

  Use the CALC menu (2ND TRACE) , and select the option ZEROS , to find  $\begin{align*}x=647.920\end{align*}$ and $\begin{align*}x=1852.080\end{align*}$ . By inspecting the graph, the solution set to the inequality $\begin{align*}-0.01x^{2}+25x-12000>0\end{align*}$ is $\begin{align*}x\in[648,1852]\end{align*}$ .
  ::使用 CALC 菜单 (2ND TRACE) , 并选择选项 ZEROS, 以找到 x= 647. 920 和 x= 1852. 080。 通过查看图表, 设定的不平等- 0.01x2+25x- 12000>0 的解决方案是 x {[648, 1852] 。

   

  播放段落

  b) What is the maximum profit McNeil can make?
  :b) McNeil所能赚取的最大利润是什么?

  播放段落

  Solution:
  ::解决方案 :

  播放段落

  Keeping the same graph open, use CALC MAXIMUM to solve for the maximum profit. The maximum is at (1250, 3625), indicating that the maximum profit is $12,625 when 1,250 wetsuits are produced.
  ::保持相同的图表打开, 使用 CALC MAXIMUM 解决最大利润问题。 最大利润为 ( 1250, 3625 ) , 表示当生产 1 250 件湿衣时, 最大利润为 12 625 美元 。

  播放段落

  Example 9
  ::例9

  播放段落

  Return to the open box problem. Use the graph provided  to determine a range of values for the side of the square, so that the volume is 30 cubic inches or greater.
  ::返回到打开框问题。 使用提供的图表来确定方形侧的值范围, 以便音量为 30 立方英寸或以上 。

  播放段落

  Solution:
  ::解决方案 :

  播放段落

  W hen the dimensions of the square cut from the corners (the height of the open box) are $\begin{align*}0.5\end{align*}$  in by  $\begin{align*}0.5\end{align*}$  in, the volume is greater than 30 cubic inches. Estimating from the graph, cutting out squares with sides between about  0.5 and 2.8 would create a box with volume 30 cubic inches or greater.
  ::当从角角切开的方形尺寸(开口箱的高度)为0.5乘0.5时,体积大于30立方英寸。 从图中估算,用0.5至2.8之间的边角切开方形,将产生一个体积为30立方英寸或以上的框。

  播放段落

  Summary
  ::摘要

  播放段落

  The method for solving polynomial and rational inequalities is the same:
  ::解决多重和合理不平等的方法是一样的:

  播放段落
  • Rewrite the inequality so that the sign of the polynomial can be tested—that is, 0 is isolated .
    ::重写不平等, 以便测试多面性标志, 也就是说, 0是孤立的 。
  播放段落
  • Find the zeros and points to divide the domain into intervals.
    ::查找零点和点,将域分成间隔。
  播放段落
  • Use test points in each interval to see which intervals satisfy the inequality.
    ::使用每个间隔的测试点来查看哪个间隔满足不平等。
  播放段落
  • Build the solution set from the table of intervals and test points.
    ::构建从间隔和测试点表格中设定的解决方案。

  播放段落

  Review
  ::回顾

  播放段落

  Find the solution set of the inequality without using a calculator: 
  ::找到不平等的解决方案集而不使用计算法:

  播放段落
  1. $\begin{align*}x^{2}+2x-3\le0\end{align*}$
     ::x2+2x-30
  播放段落
  2. $\begin{align*}3x^{2}-7x+2>0\end{align*}$
     ::3x2-7x+2>0
  播放段落
  3. $\begin{align*}-6x^{2}-13x+5\ge0\end{align*}$
     ::- 6x2-13x+50
  播放段落
  4. $\begin{align*}\frac{5x-1}{x-2}>0\end{align*}$
     ::5-1x-2>0
  播放段落
  5. $\begin{align*}\frac{1-x}{x}<1\end{align*}$
     ::1 - xx < 1
  播放段落
  6. $\begin{align*}4x^3 - 4x^2 - 3x > 0\end{align*}$
     ::4x3 - 4x2 - 3x>0
  播放段落
  7. $\begin{align*}\frac{x^4}{4} - x^2 <0\end{align*}$
     ::x44-x2 <0
  播放段落
  8. $\begin{align*}4x^3 - 8x^2 - x + 2 \geq 0 \end{align*}$
     ::4x3-8x2-x+2x0
  播放段落
  9. $\begin{align*}\frac{n^3 - 2n^2 - n + 2}{n^3 + 3n^2 + 4n + 12} < 0 \end{align*}$
     ::n3-2n2-n+2n3+3n2+4n+12 <0
  播放段落
  10. $\begin{align*}\frac{n^3 + 3n^2 - 4n - 12}{n^3 - 5n^2 + 4n - 20} \leq 0 \end{align*}$
      ::n3+3n2 - 4n - 12n3 - 5n2+4n - 200
  播放段落
  11. $\begin{align*}\frac{2n^3 + 5n^2 - 18n - 45}{3n^3 - n^2 +27n - 9} \geq 0 \end{align*}$
      ::2n3+5n2-18n-453n3-n2+27n-90
  播放段落
  12. $\begin{align*}\frac{12n^3 + 16n^2 - 3n - 4}{8n^3 +12n^2 + 10n +15} >0 \end{align*}$ 播放段落

      Use a calculator to solve the inequalities below. Round your answer to three places after the decimal.
      ::使用计算器来解决下面的不平等问题。 将您的答复四舍五入到小数点后的三个位子 。

      
      ::12n3+16n2 - 3n - 48n3+12n2+10n+15>0 使用计算器解决以下的不平等问题。您在小数点后将回答四舍五入到三位。
  播放段落
  13. $\begin{align*}-9.8t^{2}+357.6t \geq 0\end{align*}$
      ::-9.8吨2+357.6吨0
  播放段落
  14. $\begin{align*}x^{3}-5x+7 \leq -4x^{2}+18\end{align*}$
      ::x3 - 5x+7\\\\\\\\\\\\\\2+18
  播放段落
  15. $\begin{align*}\frac{x^{2}-2x}{x-5} > x^{2}-25\end{align*}$
      ::x2-2xx-5>x2-2-25
  播放段落
  16. Simplify and graph  $\begin{align*}f(x) > \frac{9x^{2}-4}{3x+2}.\end{align*}$
      ::简化和图形 f( x) > 9x2 - 43x+2 。
  播放段落
  17. The total resistance of two electronics components wired in parallel is given by $\begin{align*}\frac{R_{1}R_{2}}{R_{1}+R_{2}},\end{align*}$ where $\begin{align*}R_{1}\end{align*}$ and $\begin{align*}R_{2}\end{align*}$ are the individual resistances (in ohms) of the two components.
      播放段落
      1. If the resistance of $\begin{align*}R_{1}\end{align*}$ is 20 ohms, what is the maximum resistance of $\begin{align*}R_{2}\end{align*}$ if the total resistance must be less than 15 ohms?
         ::如果R1的抵抗力是20 ohms,那么如果总抵抗力必须低于15 ohms,那么R2的最大抵抗力是什么?
      播放段落
      2. What is the maximum theoretical resistance of this circuit? How do you know?
         ::这个电路最大的理论阻力是什么?
      
      ::R1R2R1+R2给出了平行连接的两个电子部件的总抗药性。 R1和R2是这两个部件的个人抗药性(以ohms为单位)。如果R1的抗药性是20 ohms,如果总抗药性必须小于15 ohms,R2的最大抗药性是什么?这个电路的最大理论抗药性是什么? 你怎么知道?
  播放段落
  18. A rectangular lot of land has a length that is 7 meters more than twice its width. If the area of the lot is greater than 60 square meters, what are the possible values of the widths of the lot?
      ::长方形土地的长度为7米,是其宽度的两倍以上。如果其面积大于60平方米,那么其宽度的可能值是多少?

  播放段落

  Review (Answers)
  ::回顾(答复)

  播放段落

  Please see the Appendix.
  ::请参看附录。

  播放段落

  Applications, Technological Tools
  ::应用、技术工具

  播放段落

  Solving quadratic, polynomial, and rational inequalities is much easier with a calculator. Two specific functions that a TI-83/84 calculator provides to help solve rational inequalities are:
  ::用计算器解决二次、多重和合理不平等比较容易。 TI-83/84计算器为帮助解决合理不平等提供的两个具体功能是:

  播放段落
  1. Using the calculator to graph a function and using the CALC menu to identify its roots.
     ::使用计算器绘制函数图,并使用 CALC 菜单来辨别其根部 。
  播放段落
  2. Using the table function to substitute test values into the function.
     ::使用表格函数将测试值替换到函数中。