6.3 右三角三角三角三角三角测量
章节大纲
-
Introduction
::导言Laner Property Management Company is very proactive concerning exterior maintenance. The company is also very careful to follow established workplace safety guidelines. When a worker prepared to wash all the windows on a three-story apartment building, the manager consulted workplace guidelines and learned that, for safety, the ladder needed to be long enough so that:
::Laner财产管理公司在外部维护方面非常积极主动,该公司还非常谨慎地遵守既定的工作场所安全准则。 当工人准备洗洗三层公寓楼的所有窗户时,经理咨询了工作场所准则,并了解到,为了安全起见,梯子必须足够长,以便:-
The ladder extends 3 feet above the highest point.
::梯子宽3英尺,高于最高点。 -
The bottom of the ladder forms a
angle with the ground.
::梯子底部形成一个75.5角度 与地面。

The manager knows that the tallest building on the property is 38 feet high. What is the length of the ladder required to do this job safely ?
::经理知道地产上最高的建筑是38英尺高。 安全地完成这项工作所需的梯子长度是多少?Trigonometry—in part, the study of triangles, will be needed to answer this question. Using trigonometry, if we know some angles and side lengths of a triangle , we can determine all other dimensions of the triangle.
::这个问题需要三角测量法来解答。 使用三角测量法,如果我们知道三角法的一些角度和侧长,我们可以确定三角法的所有其他维度。Introduction to Right Triangle Trigonometry
::右三角三角三角三角三角测量入门The six trigonometric functions are sine, cosine, tangent, cotangent , secant, and cosecant , where the functions' inputs are angles. For a right triangle, these functions can be determined as ratios of sides of the triangle. Opp stands for the leg opposite of the angle , hyp stands for hypotenuse, and adj stands for the leg adjacent to the angle .
::6个三角函数是正弦、正弦、正弦、正切、正切、正切、缓冲和正弦,函数输入为角度。对于右三角形,这些函数可以被确定为三角形两侧的比重。Opp代表角对面的腿,Hyp代表低压,adj代表角对面的腿。T he sine of an angle, , is defined as the leg opposite divided by the hypotenuse. The cosine of an angle, , is defined as the leg adjacent divided by the hypotenuse. The tangent of an angle, , is defined as the leg opposite divided by the leg adjacent . The cosecant of an angle, , is defined as the hypotenuse divided by the leg opposite . The secant of an angle, , is defined as the hypotenuse divided by the leg adjacent. The cotangent of an angle, , is defined as the leg adjacent divided by the leg opposite .
::角的正弦( sin) 被定义为由下限分开的正弦。 角的余弦( cos ) 被定义为由下限分开的紧腿。 角的正弦( tan ) 被下限分开的腿。 角的正弦( tan ) 被下限的正弦( train) 定义为由下限分开的腿。 角的正弦( csc ) 被下限的正弦( sec ) 被下限为由下限相邻的腿分开的下角( sec ) 。 角的正弦( cot) 被下限为相邻的腿 。 角的紧弦( cot) 被下限为由相反的腿分开的紧部 。Trigonometric Functions
::三角三角函数Basic Trigonometric Identities
::基本三角特征Notice that the sine function and cosecant function are reciprocals of each other.
::注意正弦功用和共生功能是相互对等的。Likewise, cosine and secant functions and tangent and cotangent functions are reciprocals of each other.
::顺差和分离功能以及正切和余切功能是彼此的对等功能。
::
::@tanoppadj=1cotcotcotadjopp=1tanExamples
::实例Example 1
::例1Solve for side .
::解决B侧。Solution:
::解决方案 :Since the hypotenuse is given, and is the leg opposite to the given angle , the sine function is the most appropriate to use in this problem.
::由于给定了低耗,b 是与给定角度2+7相反的腿,正弦函数是这一问题中最适当的使用。
:27) =b14b=14sin( 27) 10.9 英寸
Example 2
::例2Solve for angle .
::解决A角度的问题。Solution:
::解决方案 :This problem can be solved using sine, cosine, or tangent relationships because the opposite, adjacent, and hypotenuse lengths are all given.
::这个问题可以使用正弦、正弦或正弦关系来解决,因为相反的、相邻的和低压的长度都给出了。The argument of a sine function is always an angle. The inverse function of a sine function is arcsin or -1 function. The argument of the inverse function of a sine function is always a ratio of sides of the triangle. Inverse trigonometric functions are used to find an angle that corresponds to a trigonometric ratio.
::正弦函数的参数始终是一个角度。正弦函数的反函数是 arcsin 或 -1 函数。正弦函数的反函数的反函数参数总是三角形两边之比。反三角函数用来寻找一个与三角比相对应的角。
::弧度=513A = 513A = sin - 1(513) 0.39 弧度= 22.6Example 3
::例3Given a right triangle with , and , find the length of the hypotenuse.
::根据右三角形的 a=12, mB=20和 mC=90, 找到下限长度 。Solution:
::解决方案 :
::12ccc=12cos 20\\\12.77英寸Example 4
::例4To return to the problem in the Introduction, the bottom of the ladder forms a angle with the ground, and the manager knows that the tallest building on the property is 38 feet high. What is the length of the ladder required to safely do this job?
::回到引言中的问题,梯子底部形成一个75.5的地角,经理知道地产上最高的建筑是38英尺高。 安全地完成这项工作所需的梯子长度是多少?Solution:
::解决方案 :Step 1: Create a diagram from the given information.
::第1步:根据给定的信息创建图表。Step 2: Solve for .
::步骤2:解决L。
::75.538LL=38sin75.539.25英尺Recall that the ladder extends 3 feet above the highest point, so add 3 to the value of .
::回顾梯子宽度超过最高点3英尺,因此L值增加3英尺。
::39.25+3=42.25英尺Example 5
::例5Given where is a right angle, , and . What is ?
::鉴于 ABC , B 是 右角 , mC = 18 , c= 12 。 什么是 ?Solution:
::解决方案 :Step 1: Create a diagram from the given information.
::第1步:根据给定的信息创建图表。Step 2: Solve for a.
::步骤2:解决一个。
::{\fn黑体\fs22\bord1\shad0\3aHBE\4aH00\fscx67\fscy66\2cHFFFFFF\3cH808080}为什么? {\fn黑体\fs22\bord1\shad0\3aHBE\4aH00\fscx67\fscy66\2cHFFFFFF\3cH808080}... {\fn黑体\fs22\bord1\shad0\3aHBE\4aH00\fscx67\fscy66\2cHFFFFFF\3cH808080}...Example 6
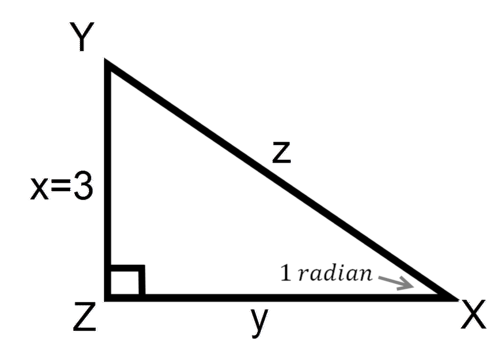
::例6Given where is a right angle, , and , what is ?
::鉴于 XYZ, Z 是右角, mX=1 弧度, x=3, 什么是 Z?Solution:
::解决方案 :Step 1: Create a diagram from the given information.
::第1步:根据给定的信息创建图表。Step 2: Solve for z.
::步骤2:解决z。
::==3zz=3sin=13.6 =3sin=3sin=1}=3.6 =3sin=3sin=3sin=1}=3.6Summary
::摘要-
The Basic Trigonometric Ratios:
-
::一九九九一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一二一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一 -
:: -
:: -
::cotadjopp 连接 -
:: -
::csc
::基本三角比率:sinopophyp cosadjhyp tanoppadj cotadjopp sechypadj cschypopp -
Review
::回顾For 1-15, information about the sides and/or angles of right triangle is given. Completely solve the triangle (find all missing sides and angles) to one decimal place. Use your knowledge of trigonometric functions, the Pythagorean Theorem, and special right triangles.
::对于 1-15 , 给出关于右三角 ABC 的边和(或) 角度的信息。 完全解析三角形( 找到所有缺失的边和角度) 到小数点后一位位 。 使用您对三角函数、 Pytagoren Theorem 和 特殊右三角形的知识 。Problem Number
::问题编号
::A A A
::BB ,B
::a a/
::b b b
::c , c , c , c1.
90°
29.745°
7
2.
90°
37°
18
3.
90°
15°
32
4.
33.06°
90°
11
5.
90°
12°
19
6.
54°
90°
10
7.
90°
10°
2
8.
4°
90°
0.3
9.
radians
::2 弧度1 radian
::1 弧度15
10.
0.93 radian
::0.93 弧度radians
::2 弧度12
11.
0.70 radian
::0.70 弧度radians
::2 弧度14
12.
radian
::4 弧度radian
::4 弧度5
13.
radians
::2 弧度26
13
14.
radians
::2 弧度1 radian
::1 弧度19
15.
radians
::2 弧度10
Review (Answers)
::回顾(答复)Please see the Appendix.
::请参看附录。 -
The ladder extends 3 feet above the highest point.