8.3 毕达哥里安三角特征

Section outline

• Select section General

  Collapse Expand

  General

  Collapse all Expand all

  • Select activity 新闻通告

    

    新闻通告 Forum
• Select section 毕达哥里安三角体特征

  Collapse Expand

  毕达哥里安三角体特征

  播放段落

  Introduction
  ::导言

  播放段落

  A data scie ntist works for an online retailer. The scientist is exploring patterns in data collected on purchasing patterns from the internet, and building mathematical functions that predict customer  spending patterns.
  ::一位数据科学家为在线零售商工作。 该科学家正在探索从互联网上收集的采购模式数据的模式,并建设预测客户支出模式的数学功能。

  

  播放段落

  To explore new graphs, the scientist graphed the function  $\begin{array}{r}y={\sin }^{2}x+{\cos }^{2}x,\end{array}$  and the graph turned out to be a straight line. Confused, the scientist wants to know why such a complicated function has such a simple graph.
  ::为了探索新的图表,科学家绘制了y=sin2x+cos2x的函数图,而图表则是一条直线。迷惑,科学家想知道为什么如此复杂的函数有这样一个简单的图表。

  播放段落

  Pythagorean Trigonometric Identities
  ::毕达哥里安三角体特征

  播放段落

  Pythagorean Trigonometric  Identities leverage the power of the to simplify trigonometric expressions.  C onsider the  $\begin{array}{r}x\end{array}$  and  $\begin{array}{r}y\end{array}$   coordinates of a point on the unit circle .  
  ::Pytagoren Trigonology 特征利用三角表达式的力量简化三角表达式。 考虑单位圆上点的 x 和 Y 坐标 。

  

  播放段落

  Since  $\begin{array}{r}\left(x,y\right)=\left(\cos \theta ,\sin \theta \right),\end{array}$  and the radius of the unit circle is 1, the Pythagorean Theorem immediately yields the identity :
  ::由于 (x,y) = (cos,sin) ,单位圆的半径为 1 , Pytagoren 理论立即生成身份 :

  播放段落

  $$\begin{array}{rl}& x^2+y^2=1\\ & {\cos }^2\theta +{\sin }^2\theta =1\\ & {\sin }^2\theta +{\cos }^2\theta =1\end{array}$$

  
  ::x2+y2=1cos2 @%sin2}%1sin2}%cos2=1

  

  播放段落

  To establish the other two Pythagorean Trigonometric Identities, start with:
  ::建立另外两个比达哥里安三角特征,首先是:

  播放段落

  $$\begin{array}{rl}{\sin }^{2}x+{\cos }^{2}x& =1\\ \frac{{\sin }^{2}x}{{\sin }^{2}x}+\frac{{\cos }^{2}x}{{\sin }^{2}x}& =\frac{1}{{\sin }^{2}x}\\ 1+{\cot }^{2}x& ={\csc }^{2}x\end{array}$$

  The proof for the other Pythagorean Trigonometric Identity , dealing with tangent and secant, will be shown in Example 3.
  ::以正切度和偏移度处理其他 Pythagoren Trigonologic 身份的证明将在例3中显示。

  播放段落

     Pythagorean Trigonometric Identities
  ::毕达哥里安三角体特征

  播放段落

  $$\begin{array}{r}{\sin }^{2}x+{\cos }^{2}x=1\\ 1+{\cot }^{2}x={\csc }^{2}x\\ {\tan }^{2}x+1={\sec }^{2}x\end{array}$$

  
  ::sin2\\ xx+cos2\\ x=11+cot2\\\\ xx=csc2\\\\ xtan2\\\\\ x+1=sec2\\\ xxx

   

   

  播放段落

  Examples
  ::实例

  播放段落

  Example 1
  ::例1

  播放段落

  Simplify the following expression: $\begin{array}{r}\frac{\sin x\cdot (\csc x-\sin x)}{1-\sin x}.\end{array}$
  ::简化以下表达式: sinx(cscx-sinx)1-sinx。

  播放段落

  Solution:
  ::解决方案 :

  播放段落

  $$\begin{array}{rl}\frac{\sin x\cdot (\csc x-\sin x)}{1-\sin x}& =\frac{\sin x\cdot \csc x-{\sin }^{2}x}{1-\sin x}\\ & =\frac{\sin x\cdot \frac{1}{\sin x}-{\sin }^{2}x}{1-\sin x}\\ & =\frac{1-{\sin }^{2}x}{1-\sin x}\\ & =\frac{(1-\sin x)(1+\sin x)}{1-\sin x}\\ & =1+\sin x\end{array}$$

  
  :cscx-sinx) 1 -sinx=sinxxxxxxxxin2xx1-sinxxx=sinxxx_sin2x1-sin2x1xx=1-sin2x1-sinxx=1-sin2x1-sinxxx1+sinx1+sinx)1-sin*x=1+sinxx=1+sinxxxxxx

  播放段落

  Note that factoring the Pythagorean Trigonometric Identity is powerful. This is a very common technique used to simplify.
  ::请注意,保理比达哥里安三角形特征具有很强的威力。 这是用来简化的非常常见的技术。

  播放段落

  Example 2
  ::例2

  播放段落

  Prove the following trigonometric identity: $\begin{array}{r}({\sec }^{2}x+{\csc }^{2}x)-({\tan }^{2}x+{\cot }^{2}x)=2\end{array}$ .
  ::证明下列三角测量特性sec2x+csc2x)-(tan2x+cot2x)=2。

  播放段落

  Solution:
  ::解决方案 :

  播放段落

  Group the terms and apply a different form of the 2nd two Pythagorean Trigonometric Identities:  $\begin{array}{r}1+{\cot }^{2}x={\csc }^{2}x\end{array}$ and $\begin{array}{r}{\tan }^{2}x+1={\sec }^{2}x\end{array}$ .
  ::组合术语并应用不同形式的第二位两位毕达哥里安三角特征:1+cot2x=csc2x和tan2x+1=sec2x。

  播放段落

  $$\begin{array}{rl}({\sec }^{2}x+{\csc }^{2}x)-({\tan }^{2}x+{\cot }^{2}x)& =2\\ ({\sec }^{2}x-{\tan }^{2}x)+({\csc }^{2}x-{\cot }^{2}x)& =2\\ 1+1& =2\end{array}$$

  
  :sec2x+csc2x)-(tan2x+cot2x)=2(se2x-tan2x)+(csc2x-cot2x)=21+1=2

  播放段落

  Example 3
  ::例3

  播放段落

  Explain the fact that cofunctions are not always connected directly through a Pythagorean identity. For example,   $\begin{array}{r}{\tan }^{2}x+{\cot }^{2}x\ne 1.\end{array}$
  ::解释共同功能并不总是通过 Pythagorean 身份直接连接的事实。 例如, tan2_\ x+cot2\\\\ x% 1 。

  播放段落

  Solution:
  ::解决方案 :

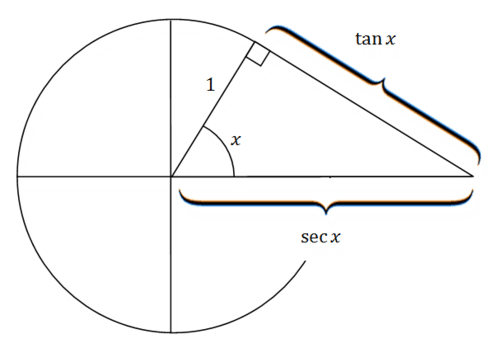
  播放段落

  Step 1: Visually, the right triangle connecting tangent and secant can also be observed in the unit circle. T angent is named "tangent" because it refers to the distance of the line tangent from the point on the unit circle to the  $\begin{array}{r}x\end{array}$ axis:    $\begin{array}{r}\tan x=\frac{opp}{adj}\end{array}$ .
  ::步骤 1: 从视觉上看, 连接正切和偏移的右三角也可以在单位圆中观测到。 Tangent 被命名为“ 切线 ” , 因为它指线切线从单位圆点到 x 轴的距离 : tanx=oppadj 。

  播放段落

  Step 2: Since the adjacent side is equal to 1 (the radius of the circle), $\begin{array}{r}\tan x\end{array}$  simply equals the opposite side. Similar logic can explain the placement of $\begin{array}{r}\sec x\end{array}$ . So,   $\begin{array}{r}{\tan }^{2}x+1={\sec }^{2}x.\end{array}$
  
  ::第2步:由于相邻侧等于 1 (圆的半径), tanx 仅等于相反的一面。 类似的逻辑可以解释 cex 的位置 。 所以, tan2x+1=sec2x 。

   

  

  播放段落

  While the above connects tangent and secant through a right triangle,  tangent and cotangent don't make up two legs of the same right triangle and thus don't add up to one for all values of x when they are squared.
  ::虽然上方通过右三角形连接正切和松散, 但正切和正切不构成同一右三角形的两条腿, 因而在平方时不等于 X 所有值的一。

  播放段落

  Example 4
  ::例4

  播放段落

  Return to the problem from the Introduction, where a data scientist works for an online retailer. The scientist graphed the function $\begin{array}{r}y={\sin }^{2}x+{\cos }^{2}x\end{array}$  and the graph was a straight line. Confused, the scientist wants to know how such a complicated function has such a simple graph.
  ::回到引言中的问题, 数据科学家为在线零售商工作。 科学家绘制了 y=sin2x+cos2x 函数图, 图表是一条直线。 迷惑了, 科学家想知道这样一个复杂的函数是如何有这样一个简单的图形的 。

  播放段落

  Solution:
  ::解决方案 :

  播放段落

  The scientist must have forgotten the Pythagorean Trigonometric Identities! By him graphing $\begin{array}{r}y={\sin }^{2}x+{\cos }^{2}x\end{array}$ , he actually graphed $\begin{array}{r}y=1\end{array}$  because $\begin{array}{r}{\sin }^{2}x+{\cos }^{2}x=1\end{array}$ . The simple graph the scientist saw was a horizontal line.
  ::科学家一定忘记了 Pythagorean Trigonology 特征! 通过他绘制 y= sin2x+cos2x, 他实际上绘制了 y=1, 因为 sin2x+cos2x=1 。 科学家看到的简单图是一个水平线 。

  播放段落

  Example 5
  ::例5

  播放段落

  Simplify the following expression:
  ::简化以下表达式:

  播放段落

  $$\begin{array}{r}({\sec }^{2}x)(1-{\sin }^{2}x)-\left(\frac{\sin x}{\csc x}+\frac{\cos x}{\sec x}\right).\end{array}$$

  
  :sec2x)(1-sin2x)-(sinxcscx+cosxsecx)。

  播放段落

  Solution :
  ::解决方案 :

  播放段落

  $$\begin{array}{r}\begin{array}{rl}& ({\sec }^{2}x)(1-{\sin }^{2}x)-\left(\frac{\sin x}{\csc x}+\frac{\cos x}{\sec x}\right)\\ & =({\sec }^{2}x)(1-{\sin }^{2}x)-\left(\frac{\sin x}{\frac{1}{\sin x}}+\frac{\cos x}{\frac{1}{\cos x}}\right)\\ & =\frac{1}{{\cos }^{2}x}\cdot {\cos }^{2}x-({\sin }^{2}x+{\cos }^{2}x)\\ & =1-1\\ & =0\end{array}\end{array}$$

  
  :sec2x) = (sinc2xxxxxxxxxx) = (sin2xxxxxxxxxx) = (sin2xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx) =1xxxxxxxxxxxxx- (sin2xxxxxxxxxxxxxxxxxxxxxx) =1-1xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx1=0

  播放段落

  Example 6
  ::例6

  播放段落

  Simplify the following expression:
  ::简化以下表达式:

  播放段落

  $$\begin{array}{r}(\cos t-\sin t{)}^2+(\cos t+\sin t{)}^2.\end{array}$$

  
  :cost-sint)2+(cost+sint)2。

  播放段落

  Solution :
  ::解决方案 :

  播放段落

  $$\begin{array}{rl}& (\cos t-\sin t{)}^2+(\cos t+\sin t{)}^2\\ & ={\cos }^{2}t-2\cos t\cdot \sin t+{\sin }^{2}t+{\cos }^{2}t+2\cos t\cdot \sin t+{\sin }^{2}t\\ & =1-2\cos t\cdot \sin t+1+2\cos t\cdot \sin t\\ & =2\end{array}$$

  
  :cosát-sint)2+(cosát+sint)2=cos2t-2costsint+sin2t+cos2}t+cos2t+2cosin}t+sin2}t=1-2cost}t+1+2cos%sin}t=2

  播放段落

  Summary
  ::摘要

  播放段落
  • The Pythagorean Identities allow for the use of the Pythagorean Theorem to simplify trigonometric expressions. They are:
    播放段落
    •   $\begin{array}{r}{\sin }^{2}x+{\cos }^{2}x=1\end{array}$  
      ::sin2\\ x x+cos2\\\\ x=1
    播放段落
    •   $\begin{array}{r}1+{\cot }^{2}x={\csc }^{2}x\end{array}$  
      ::1+cot2x=csc2x
    播放段落
    •   $\begin{array}{r}{\tan }^{2}x+1={\sec }^{2}x\end{array}$  
      ::tan2+1=sec2}*xx==sec2}*x
    
    ::Pythagorean 特征允许使用 Pythagorean 理论来简化三角表达式 。 它们是: sin2\\ x+cos2x= 1 1+cot2x=csc2x tan2xx+1=sec2x

  播放段落

  Review
  ::回顾

  播放段落

  Prove each of the following:
  ::证明以下各点:

  播放段落

  1.  $\begin{array}{r}(1-{\cos }^{2}x)(1+{\cot }^{2}x)=1\end{array}$
  ::1. (1 - cos2x)(1+cot2x)=1

  播放段落

  2. $\begin{array}{r}\cos x(1-{\sin }^{2}x)={\cos }^{3}x\end{array}$
  ::2. COsx(1- 辛2x) =cos3x

  播放段落

  3.  $\begin{array}{r}{\sin }^{2}x=(1-\cos x)(1+\cos x)\end{array}$
  ::3 sin2 x = (1 - cosx (1+cosx))

  播放段落

  4.  $\begin{array}{r}\sin x=\frac{{\sin }^{2}x+{\cos }^{2}x}{\csc x}\end{array}$
  ::4. sin *x=sin2*x+cos2*xcsc*x

  播放段落

  5.  $\begin{array}{r}{\sin }^{4}x-{\cos }^{4}x={\sin }^{2}x-{\cos }^{2}x\end{array}$
  ::5 sin4x-cos4x=sin2x-cos2xxx

  播放段落

  6.  $\begin{array}{r}{\sin }^{2}x{\cos }^{3}x=({\sin }^{2}x-{\sin }^{4}x)(\cos x)\end{array}$
  ::6.2xcos3x=( 辛2x- 辛4x) (cosx)

  播放段落

  Simplify:
  ::简化 :

  播放段落

  7.  $\begin{array}{r}{\tan }^{3}x{\csc }^{3}x\end{array}$
  ::7.3xcsc3x

  播放段落

  8.  $\begin{array}{r}\frac{{\csc }^{2}x-1}{{\sec }^{2}x}\end{array}$
  ::8. csc2x-1sec2x

  播放段落

  9.  $\begin{array}{r}\frac{1-{\sin }^{2}x}{1+\sin x}\end{array}$
  ::9. 1 - 辛2x1+辛%x

  播放段落

  10.  $\begin{array}{r}\sqrt{1-{\cos }^{2}x}\end{array}$
  ::10. 1 - COs2 x

  播放段落

  11.  $\begin{array}{r}\frac{{\sin }^{2}x-{\sin }^{4}x}{{\cos }^{2}x}\end{array}$
  ::11.2x-sin4xxcos2xxxxxxxxxxxxxxxx

  播放段落

  12.  $\begin{array}{r}(1+{\tan }^{2}x)({\sec }^{2}x)\end{array}$
  ::12. (1+tan2x)(sec2x)

  播放段落

  13.  $\begin{array}{r}\frac{{\sin }^{2}x+{\tan }^{2}x+{\cos }^{2}x}{\sec x}\end{array}$
  ::13.2x+tan2x+cos2xxsecxxxxxxxxxxxxxx

  播放段落

  14.  $\begin{array}{r}\frac{1+{\tan }^{2}x}{{\csc }^{2}x}\end{array}$
  ::14. 1+tan2xcsc2x

  播放段落

  15.  $\begin{array}{r}\frac{1-{\sin }^{2}x}{\cos x}\end{array}$
  ::15. 1 - 辛2xcosxx

  播放段落

  Review (Answers)
  ::回顾(答复)

  播放段落

  Please see the Appendix.
  ::请参看附录。