Course: 11.6 超双螺旋体 | The Way To Learn

Section outline

Select section General

Collapse Expand
General

Collapse all Expand all
- Select activity 新闻通告
  
  新闻通告 Forum
Select section 超双

Collapse Expand
超双
Introduction
::导言

Hyperbolas can be oriented so they open side to side or up and down. How can we determine the direction of the opening of a hyperbola by the equation? Hyperbolas are relations that have asymptotes. When graphing rational functions, you often produce a hyperbola. In this concept, hyperbolas will not be oriented in the same way as with rational functions, but the basic shape of a hyperbola will still be there.
::Hyperbolas可以调整方向,让它们向上向上或向下开开来。我们如何用方程式来决定打开双倍波拉的方向? Hopbolas 是具有无等同元素的关系。在绘制理性函数图时,你常常产生双倍波拉。在这个概念中,双倍波拉不会以与理性函数相同的方式向上,但双倍波拉的基本形状仍然存在。

The Hyperbola
::双波

Recall that a hyperbola is generated when a plane intersects both nappes of the cone. As a result, a hyperbola has two foci . For every point on the hyperbola, the difference of the distances to each foci is constant.
::提醒注意当一平面交叉锥锥体的两个腺时会产生双波拉。因此, 双波拉有两个角。对于双波拉的每一点, 与每个角的距离是恒定的。

Standard Equation of a Hyperbola
::超重波体的标准方程式

The graphing form of a hyperbola that opens side to side is
::向侧打开的双倍波拉的图形形式是

$\begin{aligned} \frac{(x - h)^{2}}{a^{2}} - \frac{(y - k)^{2}}{b^{2}} = 1, \end{aligned}$

:x-h)2a2-(y-k)2b2=1,

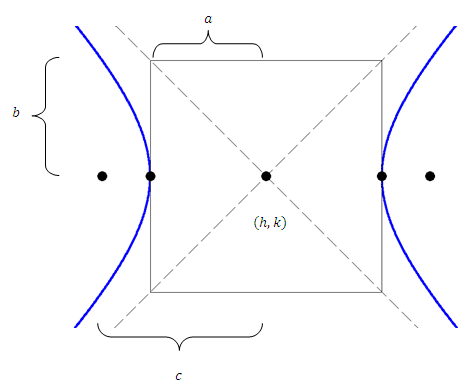
where $\begin{aligned} (h, k) \end{aligned}$ is the center of the hyperbola, $\begin{aligned} a \end{aligned}$ is the semi-major axis , and $\begin{aligned} b \end{aligned}$ is the semi-minor axis .
::其中 (h, k) 是超波拉的中心, a 是半主轴, b 是半最小轴。

A hyperbola that opens up and down is
::上上下上下打开的双波波拉

$\begin{aligned} \frac{(y - k)^{2}}{a^{2}} - \frac{(x - h)^{2}}{b^{2}} = 1, \end{aligned}$
where $\begin{aligned} (h, k) \end{aligned}$ is the center of the hyperbola, $\begin{aligned} a \end{aligned}$ is the semi-major axis, and $\begin{aligned} b \end{aligned}$ i s the semi-minor axis .
:y)(k)2a2-(x-h)2b2=1,其中(h,k)是超波拉的中心,a是半主轴,b是半最小轴。

Notice that for hyperbolas, $\begin{aligned} a \end{aligned}$ goes with the positive term and $\begin{aligned} b \end{aligned}$ goes with the negative term. It does not matter which constant is larger.
::请注意,对于超光子, 使用正值术语和 b 使用负值术语。哪个恒定值更大并不重要。

When graphing, the constants $\begin{aligned} a \end{aligned}$ and $\begin{aligned} b \end{aligned}$ enable you to draw a rectangle around the center. The transverse axis travels from vertex to vertex and has length $\begin{aligned} 2 a \end{aligned}$ . The conjugate axis travels perpendicular to the transverse axis through the center and has length $\begin{aligned} 2 b \end{aligned}$ . The foci lie beyond the vertices so the eccentricity, which is measured as $\begin{aligned} e = \frac{c}{a} \end{aligned}$ , is larger than 1 for all hyperbolas. Hyperbolas also have two directrix lines that are $\begin{aligned} \frac{a^{2}}{c} \end{aligned}$ away from the center (not shown on the image).
::当图形绘制时,常数 a 和 b 使您能够在中心周围绘制矩形。横轴从顶部向顶部移动, 长度为 2a 。共振轴通过中心垂直到横轴, 长度为 2b 。顶部位于顶部之外, 因此以 e=ca 测量的偏心度大于 1 , 对所有双波las 来说, 超双波las 的偏心度大于 1 。 Hyperbolas 也有两条直径直线, 离中心有 A2c 距离( 未显示在图像上 ) 。

The focal radius is given by $\begin{aligned} c \end{aligned}$ where $\begin{aligned} a^{2} + b^{2} = c^{2} \end{aligned}$ .
::焦半径由 a2+b2=c2 的 c 给出。

The following video defines a hyperbola and explains how to graph a hyperbola given in standard form:
::以下视频定义了超重波拉,并解释了如何用标准格式绘制超重波拉图:

The following video explains how to graph a hyperbola in general form:
::以下影片解释如何用一般形式绘制双倍波拉图:

Play, Learn, and Explore Hyperbolas:
::玩耍、学习和探索超双人游戏:

Examples
::实例

Example 1
::例1

Put the following hyperbola into graphing form and sketch it:
::将以下双倍波拉放入图形形状和草图:

$\begin{aligned} 9 x^{2} - 4 y^{2} + 36 x - 8 y - 4 = 0. \end{aligned}$

::9x2-4y2+36x-8y-4=0。

Solution:
::解决方案 :

$\begin{aligned} 9 (x^{2} + 4 x) - 4 (y^{2} + 2 y) & = 4 \\ 9 (x^{2} + 4 x + 4) - 4 (y^{2} + 2 y + 1) & = 4 + 36 - 4 \\ 9 (x + 2)^{2} - 4 (y + 1)^{2} & = 36 \\ \frac{(x + 2)^{2}}{4} - \frac{(y + 1)^{2}}{9} & = 1 \end{aligned}$

::9(x2+4x)-4(y2+2y)=49(x2+4x+4)-4(y2+2y+1)=4+36-49(x+2)-2-4(y+1)-2-4(y+1)=36(x+2)=36(x+2)24-(y+1)29=1

Example 2
::例2

Find the equation of the hyperbola with foci at (-3, 5) and (9, 5) and asymptotes with slopes of $\begin{aligned} \pm \frac{4}{3} \end{aligned}$ .
::查找超重波拉方位( 3, 5) 和( 9, 5) 的方位方位, 以及斜度为 +43 的单位方位方位。

Solution:
::解决方案 :

The center is between the foci at (3, 5). The focal radius is $\begin{aligned} c = 6 \end{aligned}$ . The slope of the asymptotes is always the rise over run inside the box. In this case, since the hyperbola is horizontal and $\begin{aligned} a \end{aligned}$ is in the $\begin{aligned} x \end{aligned}$ direction, the slope is $\begin{aligned} \frac{b}{a} \end{aligned}$ . This makes a system of equations.
::中心位于( 3, 5 ) 的角之间, 焦半径为 c=6 。小微粒的斜度总是在框内运行的上升。在这种情况下, 由于双倍波拉是水平的, a 是向 x 方向的, 斜度是 ba 。这就形成了一个方程系统。

$\begin{aligned} \frac{b}{a} & = \pm \frac{4}{3} \\ a^{2} + b^{2} & = 6^{2} \end{aligned}$

::巴瓦43a2+b2=62

When you solve, you get $\begin{aligned} a = 3.6 and b = 4.8 \end{aligned}$ .
::解决后,将获得a=3.6和b=4.8。

$\begin{aligned} \frac{(x - 3)^{2}}{\frac{324}{25}} - \frac{(y - 5)^{2}}{\frac{576}{25}} = 1 \end{aligned}$

:x-3)232425-(y-5)257625=1

Example 3
::例3

Find the equation of the conic that has a focus point at (1, 2), a directrix at $\begin{aligned} x = 5 \end{aligned}$ , and an eccentricity equal to $\begin{aligned} \frac{3}{2} \end{aligned}$ . Use the property that the distance from a point on the hyperbola to the focus is equal to the eccentricity times the distance from that same point to the directrix:
$\begin{aligned} \bar{P F} = e \bar{P D} . \end{aligned}$
Solution:
::找到在(1, 2) 有焦点点的二次曲线的方程式、 x=5 的直线和等于 32. 的偏心度。使用以下属性: 从超博拉点到焦点点的距离等于从同一点到直线点的偏心度乘数: PF = ePD 。解决方案 :

This relationship bridges the gap between , which have eccentricity less than 1, and hyperbolas, which have eccentricity greater than 1. When eccentricity is equal to 1, the shape is a parabola .
::这种关系弥合了偏心度小于1的偏心度与偏心度大于1的超陈代谢值之间的差距。当偏心度等于1时,形状即为抛物线。

$\begin{aligned} \sqrt{(x - 1)^{2} + (y - 2)^{2}} = \frac{3}{2} \sqrt{(x - 5)^{2}} \end{aligned}$

:x-1)2+(y-2)2=32(x-5)2

Square both sides and rearrange terms so that it becomes a hyperbola in graphing form.
::方形两侧和重新排列的词义,以图示形式使它变成双波形。

$\begin{aligned} x^{2} - 2 x + 1 + (y - 2)^{2} & = \frac{9}{4} (x^{2} - 10 x + 25) \\ x^{2} - 2 x + 1 - \frac{9}{4} x^{2} + \frac{90}{4} x - \frac{225}{4} + (y - 2)^{2} & = 0 \\ 4 x^{2} - 8 x + 4 - 9 x^{2} + 90 x - 225 + 4 (y - 2)^{2} & = 0 \\ - 5 x^{2} + 82 x - 221 + 4 (y - 2)^{2} & = 0 \\ - 5 (x^{2} + \frac{82}{5} x + \frac{1681}{25}) + 4 (y - 2)^{2} & = 221 - \frac{1681}{5} \\ - 5 {(x + \frac{41}{5})}^{2} + 4 (y - 2)^{2} & = - \frac{576}{5} \\ \frac{25 {(x + \frac{41}{5})}^{2}}{576} - \frac{5 (y - 2)^{2}}{144} & = 1 \end{aligned}$

::x2 - 2x+1+1+(y-2-2)2=94(x2-10x+25)2=94(x2-10x+25)2x2x-2-2-2x-2-2x-2-942-942-904x-2254+(y-2)2=042x-8x+8x+4-9x2-9x2-90x2+90x2-9x2-9x2+9x2-90x2-90x2+9x2-2-90x2x2=0-5x2+822x-2211+4(y2-2)2=0-5(x2+825xx-1825x+168252525)+4-155(x+415)2-57652525(x+4-156-5(y-244=1)

Example 4
::例4

Recall the problem from the Introduction: How can we determine the direction of the opening of a hyperbola by the equation?
::回顾导言中的问题:我们如何用方程式确定超重波拉打开的方向?

Solution:
::解决方案 :

Consider the hyperbola $\begin{aligned} x^{2} - y^{2} = 1 \end{aligned}$ . This hyperbola opens side to side because $\begin{aligned} x \end{aligned}$ can never be equal to zero. This example demonstrates that when the coefficient of the $\begin{aligned} y \end{aligned}$ value is negative, the hyperbola opens up side to side.
::考虑超bola x2- y2= 1 。此超bola 打开侧面, 因为 x 永远不能等于 0。此示例显示, 当 y 值的系数为负时, 超bola 打开侧面。

Example 5
::例5

Identify the shape, center, foci, vertices, equations of asymptotes, and equations of directrices of the following conic:
::识别以下二次曲线的形状、中位、角、角、脊椎、小微粒方程式和直线方程式:

$\begin{aligned} 9 x^{2} - 16 y^{2} - 18 x + 96 y + 9 = 0. \end{aligned}$

::9x2 - 16y2 - 18x+96y+9=0。

Solution:
::解决方案 :

$\begin{aligned} 9 x^{2} - 16 y^{2} - 18 x + 96 y + 9 = 0 \end{aligned}$

::9x2-16y2-18x+96y+9=0

$\begin{aligned} 9 (x^{2} - 2 x) - 16 (y^{2} - 6 y) & = - 9 \\ 9 (x^{2} - 2 x + 1) - 16 (y^{2} - 6 y + 9) & = - 9 + 9 - 144 \\ 9 (x - 1)^{2} - 16 (y - 3)^{2} & = - 144 \\ - \frac{(x - 1)^{2}}{16} + \frac{(y - 3)^{2}}{9} & = 1 \end{aligned}$

::9(x2-2x)-16(y2-6y) 99(x2-2x+1)-16(y2-6y+9) 9+9-1449(x-1) 2-16(y-3) 2-144-(x-1) 216+(y-3)29=1

Shape: Hyperbola that opens vertically
::形状:垂直打开的超博拉

Center: (1, 3)
::中心1,3)

$\begin{aligned} a = 3 \end{aligned}$
::a=3 =3

$\begin{aligned} b = 4 \end{aligned}$
::b=4 =4

$\begin{aligned} c = 5 \end{aligned}$
::c=5 个

$\begin{aligned} e = \frac{c}{a} = \frac{5}{3} \end{aligned}$
::e=ca=53

$\begin{aligned} d = \frac{a^{2}}{c} = \frac{9}{5} \end{aligned}$
::d=a2c=95 =95

Foci: (1, 8), (1, -2)
::实任1,8),(1,2)

Vertices: (1, 6), (1, 0)
::顶点1,6),(1,0)

Equations of asymptotes: $\begin{aligned} (x - 1) = \pm \frac{3}{4} (y - 3) \end{aligned}$
::微粒量的等同度x-1) 34(y-3)

Note that it is easiest to write the equations of the asymptotes in point-slope form using the center and the slope.
::请注意,使用中间和斜坡以点窗体形式以点窗体写出小数方程是最容易的。

Equations of directrices: $\begin{aligned} y = 3 \pm \frac{9}{5} \end{aligned}$
::电流平方:y=395

Example 6
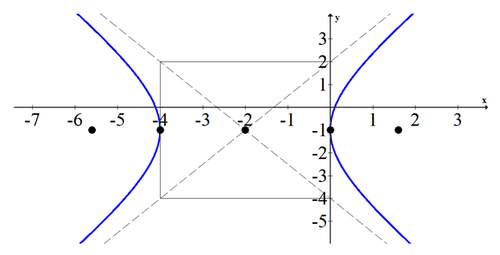
::例6

Given the graph below, estimate the equation of the conic.
::根据下图,估计二次曲线的方程。

Solution:
::解决方案 :

Since exact points are not marked, you will need to estimate the slope of asymptotes to get an approximation for $\begin{aligned} a \end{aligned}$ and $\begin{aligned} b \end{aligned}$ . The slope seems to be about $\begin{aligned} \pm \frac{2}{3} \end{aligned}$ . The center seems to be at (-1, -2). The transverse axis is 6, which means $\begin{aligned} a = 3 \end{aligned}$ .
::由于未标出精确点, 您需要估计小行星的斜度, 才能得出 a 和 b 的近似值。斜度似乎是 + 23 。中心似乎在 (-1 - 2) , 横轴是 6 , 这意味着 a= 3 。

$\begin{aligned} \frac{(x + 1)^{2}}{9} - \frac{(y + 2)^{2}}{4} = 1 \end{aligned}$
:x+1)29-(y+2)24=1

Example 7
::例7

Find the equation of the hyperbola that has foci at (13, 5) and (-17, 5), with asymptote slopes of $\begin{aligned} \pm \frac{3}{4} . \end{aligned}$
::查找具有福子值(13,5)和(17,5)的超重波拉的方程,以微量斜度为 +34。

Solution:
::解决方案 :

The center of the conic must be at (-2, 5). The focal radius is $\begin{aligned} c = 15 \end{aligned}$ . The slopes of the asymptotes are $\begin{aligned} \pm \frac{3}{4} = \frac{b}{a} \end{aligned}$ .
::二次曲线的中心必须位于 (-2, 5) 。焦半径为 c=15。小行星的斜度为 34 =ba 。

$\begin{aligned} a^{2} + b^{2} = c^{2} \end{aligned}$
::a2+b2=c2 = c2 =

Since 3, 4, 5 is a well-known Pythagorean triple, it should be clear to you that $\begin{aligned} a = 12, b = 9. \end{aligned}$
::3,4,4,5是众所周知的毕达哥林三联赛, 你应该清楚,a=12,b=9。

$\begin{aligned} \frac{(x + 2)^{2}}{12^{2}} - \frac{(y - 5)^{2}}{9^{2}} = 1 \end{aligned}$ .
:x+2)2122-2(y-5)292=1。

Summary
::摘要

A hyperbola is the collection of points that share a constant difference between the distances between two focus points.
::双倍波拉是收集在两个焦点点之间的距离之间始终存在差异的点数。

Eccentricity is the ratio between the length of the focal radius and the length of the semi-transverse axis. For hyperbolas, the eccentricity is greater than 1.
::偏心度是焦半径长度与半反向轴长度之比。对于超光子,偏心度大于1。

The graphing form of a hyperbola that opens side to side is
::向侧打开的双倍波拉的图形形式是

$\begin{aligned} \frac{(x - h)^{2}}{a^{2}} - \frac{(y - k)^{2}}{b^{2}} = 1 \end{aligned}$ .
:x-h)2a2-(y-k)2b2=1。

::向侧打开的双倍波拉的图形形式是 (x-h) 2a2 - (y-k) 2b2=1 。

The graphing form of a hyperbola that opens up and down is
::向上和向下打开的超双波拉的图示形式是

$\begin{aligned} \frac{(y - k)^{2}}{a^{2}} - \frac{(x - h)^{2}}{b^{2}} = 1 \end{aligned}$ .
:y-k)2a2-(x-h)2b2=1。

::向上和向下打开的双倍波拉的图形形式是 (y-k) 2a2 - (x-h) 2b2=1。

Review
::回顾

Use the following equation for 1-5: $\begin{aligned} x^{2} + 2 x - 4 y^{2} - 24 y - 51 = 0. \end{aligned}$
::1-5使用以下方程式: x2+2x-4y2-24y-51=0。

1. Put the hyperbola into graphing form. Explain how you know it is a hyperbola.
::1. 将双波拉放入图形形式,解释你如何知道它是双波拉。

2. Identify whether the hyperbola opens side to side or up and down.
::2. 确定超重波拉是向侧还是向上或向下打开。

3. Find the location of the vertices.
::3. 找到顶点的位置。

4. Find the equations of the asymptotes.
::4. 寻找小行星的方程。

5. Sketch the hyperbola.
::5. 伸展双倍波拉。

Use the following equation for 6-10: $\begin{aligned} - 9 x^{2} - 36 x + 16 y^{2} - 32 y - 164 = 0. \end{aligned}$
::6-10时使用以下方程式:-9x2-36x+16y2-32y-164=0。

6. Put the hyperbola into graphing form. Explain how you know it is a hyperbola.
::6. 将双波拉放入图形形式,解释你如何知道它是双波拉。

7. Identify whether the hyperbola opens side to side or up and down.
::7. 确定超重波拉是向侧还是向上或向下打开。

8. Find the location of the vertices.
::8. 寻找顶峰的位置。

9. Find the equations of the asymptotes.
::9. 寻找小行星的方程。

10. Sketch the hyperbola.
::10. 涂抹双倍波拉。

Use the following equation for 11-15: $\begin{aligned} x^{2} - 6 x - 9 y^{2} - 54 y - 81 = 0. \end{aligned}$
::11-15 使用以下方程式: x2-6x-9y2-54y-81=0。

11. Put the hyperbola into graphing form. Explain how you know it is a hyperbola.
::11. 将双波拉放入图形形式,解释你如何知道它是双波拉。

12. Identify whether the hyperbola opens side to side or up and down.
::12. 确定超重波拉是向上向上向下打开侧侧还是向上向上向下打开。

13. Find the location of the vertices.
::13. 寻找顶峰的位置。

14. Find the equations of the asymptotes.
::14. 寻找小行星的方程。

15. Sketch the hyperbola.
::15. 涂抹双倍波拉。

Review (Answers)
::回顾(答复)

Please see the Appendix.
::请参看附录。

Section outline

General

超双

Introduction ::导言

The Hyperbola ::双波

Standard Equation of a Hyperbola ::超重波体的标准方程式

Examples ::实例

Summary ::摘要

Review ::回顾

Review (Answers) ::回顾(答复)

Introduction
::导言

The Hyperbola
::双波

Standard Equation of a Hyperbola
::超重波体的标准方程式

Examples
::实例

Summary
::摘要

Review
::回顾

Review (Answers)
::回顾(答复)