12.2 极地坐标系统

Section outline

• Select section General

  Collapse Expand

  General

  Collapse all Expand all

  • Select activity 新闻通告

    

    新闻通告 Forum
• Select section 极地坐标系统

  Collapse Expand

  极地坐标系统

  播放段落

  Introduction
  ::导言

  

  播放段落

  When traveling a long distance from one place to another , walking, biking, or driving takes considerably more time than flying. One obvious reason is the faster speed of air travel, as well as the extra traffic on the roadways. Another reason is that the coordinate system that most roads are based upon limit s the movement to north, south, east, and west. For instance, when w alking or driving, you may go east two blocks, turn left, go north six blocks, and then have to wait for a train to pass. Then you may turn right, go east three more blocks, turn left, go north four more blocks, and then finally park. However, when flying you may fly 30 ^o  east of north for a little less than 11 $\begin{align*}\frac{1}{4}\end{align*}$  blocks, and then you land. Your flight is based upon the polar coordinate system. 
  ::当长途旅行从一个地方到另一个地方,步行、骑自行车或驾驶比飞行花费的时间要长得多时,一个明显的原因是空中旅行速度更快,以及公路上的额外交通。另一个原因是,大多数道路的坐标系统基于限制向北、南、东和西移动。例如,行走或驾驶时,你可以往东走两个街区,左转,向北走六个街区,然后必须等待火车过路。然后,你可以向右转,往东走三个街区,向左转,往北走四个街区,然后是停车。然而,当飞行时,你可以向北飞30o,到不到1114个街区,然后降落。你的飞行以极地坐标系统为基础。

  播放段落

  Polar Coordinate System
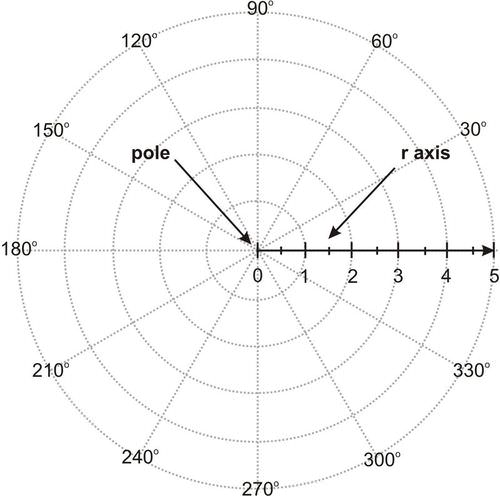
  ::极地坐标系统

  播放段落

  The polar coordinate system is an alternative to the Cartesian (rectangular) coordinate system. Where the Cartesian system identifies position east and north of a fixed reference point (the origin), the polar coordinate system measures location using direction and distance from a fixed reference point (the pole).
  ::极地坐标系统是笛卡尔(矩形)坐标系统的一种替代办法。当笛卡尔系统确定固定参考点(原点)的东面和北面位置时,极地坐标系统使用固定参考点(原点)的方向和距离测量位置。

  播放段落

  Points in the polar coordinate system are given in the form $\begin{align*}\left(r, \theta \right)\end{align*}$ .  The polar axis, or  $\begin{align*}r\end{align*}$ -axis,  is referring to the polar radius $\begin{align*}r\end{align*}$ . To plot a specific point, first find the point that is  $\begin{align*}r\end{align*}$ units from the origin on the polar axis . Then, rotate counterclockwise by the given angle, commonly represented as $\begin{align*}\theta\end{align*}$ . Be certain  to use the correct units for the angle measure (either radians or degrees).  Angles are identified by traveling counterclockwise around the circular graph from the 0° line, or polar axis (where the positive - axis would be), to a specified angle. Note that you can choose to travel $\begin{align*}\theta^\circ\end{align*}$  counterclockwise, or you can reach the same location by traveling $\begin{align*}(360-\theta)^\circ\end{align*}$ in the clockwise direction. For example, traveling 230° counterclockwise is the same as traveling 130° clockwise. 
  ::极地坐标系统中的点以窗体表示(r, ) 。 极轴或 r- 轴是指极半径 r 。 要绘制一个特定的点, 请先从极轴的原点找到 r 单位。 然后, 以给定角度逆时旋转, 通常代表 } 。 确定要使用正确的单位来测量角( 弧度或度) 。 角是通过逆时针绕圆形图从 0 o 线或极轴( 正轴在正轴处) 绕圆形向指定角度移动来识别的。 注意您可以选择逆时针运行 { } , 或者您可以在时针方向旅行 ( 360 } ) 。 例如, 逆时针旅行 230 等于 130 时针 。

  

  播放段落

  When using , the angle is usually stated using either degree measure or . On the Cartesian coordinate system, you can define a radian as the angle created by the $\begin{align*}x\end{align*}$ -axis and another radius of a circle centered at the origin where the arclength on the edge of the circle equals the radius. Similarly, a  radian is the angle formed between the  polar axis and the terminal side lying on the line passing through the point and the pole. 
  ::当使用时,角度通常使用度量或 。在笛卡尔坐标系统中,您可以将弧度定义为由X轴和圆角另一半径所创建的角,圆角以圆边边缘的弧长等于半径的原点为中心。同样,弧度是极轴和横穿点和极线的终点端之间形成角。

  播放段落

      Graphing Using Technology  
  ::利用技术图图绘制图图

  播放段落

  Polar equations can be graphed using online graphing software (e.g. Desmos or GeoGebra) or a graphing calculator.
  ::可使用在线图形化软件(例如,Desmos或GeoGebra)或图形化计算器绘制极地方程式图。

  播放段落

  With the graphing calculator, go to MODE . There, select RADIAN for the angle measure, and POL (for polar) on the FUNC (function) line. When Y = is pressed, note that the equation has changed from y = to r = . There, input the polar equation. After pressing graph, if you can’t see the full graph, adjust x - and y - max/min, etc. in WINDOW.
  ::使用图形计算器, 转到 MODE 。 在那里, 选择 RADIAN 用于角度量, 并在 FUNC (函数) 线上选择 POL( 极值) 。 当 Y = 被按下时, 注意方程式已经从 y = 改为 r = 。 在那里, 输入极性方程 。 在按下图后, 如果您在 WINDOW 中看不到完整图形, 请调整 x 和 y 最大/ min 等 。

  播放段落

  In Desmos, choose SETTINGS  (the icon that looks like a wrench). In the graph paper section, you can change the grid and axes. Click the green circular icons to choose between Cartesian and polar grids, and show or hide axes labels. You can also select whether you would like the graph to show radians or degrees at the bottom of this menu.
  ::在 Desmos 中,选择 Settings (看起来像扳手的图标)。在图形纸部分,您可以更改网格和轴。单击绿色圆形图标,在笛卡尔和极地网格中选择,并显示或隐藏轴标签。您也可以选择您是否想要图形显示此菜单底部的弧度或度。

   

  播放段落

  The video below distinguishes between the rectangular coordinate system and the polar coordinate system. It also demonstrates how to plot points using the polar coordinate system.
  ::以下视频区分矩形坐标系统和极地坐标系统,并演示如何使用极地坐标系统绘制点。

   

   

   

   

   

  播放段落

  Multiple equivalent representations of ( $\begin{align*}r,\theta\end{align*}$ )
  :r,_________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

  播放段落

  Angles can be represented in more than one way. For example, angles 35° and  395º are coterminal . In the polar plane, a point can be represented by more than one pair of polar coordinates.
  ::角度可以不止一种方式表示。 例如, 角度 35 ° 和 395 o 是共白度。 在极平面上, 点可以由多个极坐标对面表示 。

  播放段落

  When  $\begin{align*}(r,\theta )\end{align*}$   and   $\begin{align*}(r',\theta' )\end{align*}$ are polar coordinates where $\begin{align*}r\neq 0\end{align*}$  and   $\begin{align*}r'\neq 0,\end{align*}$  then  $\begin{align*}(r,\theta )\end{align*}$ and $\begin{align*}(r',\theta' )\end{align*}$ determine the same point P, if and only if one of the following is true:
  ::当 (r, ) 和 (r, ) 是极地坐标, 其中r0 和 r0, 然后(r, ) 和 (r, ) 确定同一点 P 时, 如果且只有在以下之一属实时:

  播放段落
  • $\begin{align*}r'=r\end{align*}$  and  $\begin{align*}\theta'=\theta +2\pi k\end{align*}$  for some integer  $\begin{align*}k.\end{align*}$
    ::rr 和 2k 表示某些整数 k。
  播放段落
  • $\begin{align*}r'=-r\end{align*}$  and  $\begin{align*}\theta'=\theta +(2k+1)\pi \end{align*}$  for some integer  $\begin{align*}k.\end{align*}$
    ::rr 和 ( 2k+1) + 用于某些整数 k 。

  播放段落

  The following illustrates that a 45° angle is equivalent to a -315° angle, as well as equivalent to a 405° angle on the polar coordinate plane: 
  ::以下说明一个45度角相当于一个-315度角,以及极地坐标平面上一个405度角:

  

  播放段落

  The following video  provides an example of the different ways to identify a point with polar coordinates using radians:
  ::以下影片举例说明了用弧度用极地坐标确定点的不同方式:

   

   

   

   

    

  播放段落

  Explore, Play, and Learn with Polar Coordinates:  .
  ::用极地坐标探索、玩耍和学习: .

  播放段落

  Examples
  ::实例

  播放段落

  Example 1
  ::例1

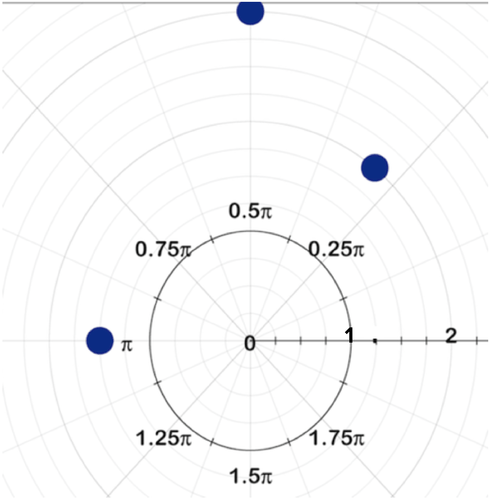
  播放段落

  Plot the points on a polar coordinate graph:
  ::在极坐标图上绘制点 :

  播放段落

  Point A $\begin{align*}\left (2,\frac{\pi}{3}\right )\end{align*}$
  ::A点(2,%3)

  播放段落

  Point B $\begin{align*}(4, 135^{o})\end{align*}$
  ::B点(4 135o)

  播放段落

  Point C $\begin{align*}\left (-2,\frac{\pi}{6}\right )\end{align*}$
  ::C点(-2,6)

  播放段落

  Solution:
  ::解决方案 :

  播放段落

  Below is the pole, polar axis, and the points A, B, and C.
  ::下面是极、极轴和A、B和C点。

  

  播放段落

  Example 2
  ::例2

  播放段落

  Determine the coordinates of the following points using radians:
  ::使用弧度确定下列点的坐标:

  

  播放段落

  Solution:
  ::解决方案 :

  1.   $\begin{align*}(4, \frac{\pi}{6})\end{align*}$
  2.   $\begin{align*}(2.5, \pi)\end{align*}$
  3.   $\begin{align*}\left(1,\frac{4\pi}{3}\right )\end{align*}$
  4.   $\begin{align*}\left(3,\frac{5\pi}{6}\right )\end{align*}$
  5.   $\begin{align*}(2, \frac{2\pi}{3})\end{align*}$

  播放段落

  Example 3
  ::例3

  播放段落

  Plot the points on a polar graph:
  ::在极图上绘制点数 :

  a) $\begin{align*}\left(2, \frac{\pi}{3}\right)\end{align*}$

  b) $\begin{align*}(3, 90^o)\end{align*}$

  c) $\begin{align*}(1.5, \pi)\end{align*}$

  播放段落

  Solution:
  ::解决方案 :

  播放段落

  The points are plotted on the graph below:
  ::这些点绘制在下图中:

  

  播放段落

  Example 4
  ::例4

  播放段落

  Recall the situation in the Introduction: Your flight is traveling 30° east of north for a little less than 11 $\begin{align*}\frac{1}{4}\end{align*}$  blocks prior to landing. What is the polar coordinate point that best represents this situation? Graph this point. 
  ::回顾导言中的情况:您的航班在着陆前在北纬30度以东行驶,飞行区块小于1114个。最能代表这种情况的极地坐标点是什么? 请绘制此点图。

  播放段落

  Solution:
  ::解决方案 :

  播放段落

  The polar radius for the flight is 11.25 blocks. 
  ::飞行的极半径为11.25个区块。

  播放段落

  The polar axis corresponds to the east direction, and angles are identified by traveling counter-clockwise around the circular graph from the polar axis. The flight is traveling 30° east of north, which means the flight is 30° clockwise from north. To get the corresponding angle traveling counterclockwise from east (or the polar axis), subtract the 30° from 90°, because north is 90° from the polar axis. 

  $$\begin{align*}\theta = 90^\circ-30^\circ =60^\circ\end{align*}$$
  ::极轴与东向对齐, 角度通过从极轴绕圆形图反时针运行来识别。 飞行在北向以东 30 °, 这意味着从北飞行为时时钟30 °。 要从东( 或极轴) 获得相应的逆时针运行角度, 从90 °减去 30 °, 因为北距离极轴90 ° 。 @ 90\\ 30\ 60\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\ 30\\\\\\\\\\\\\\\\\\\ 30\\\\\\\\\\\\\ 30\\\\\\\\\\\\\ \\\\\\ \ \ \ \ \ \ \\\\ \ \ \ \ \\\\\\\ \ \ \ \ \ \ \ \\\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\ \ \ \ \\ \ \ \ \\\\\\\\\\\\\ \ \ \ \ \\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\

  播放段落

  Thus, the polar coordinate is  $\begin{align*}(11.25, 60^\circ)\end{align*}$ . 
  ::因此,极地坐标是(11.25,60)。

  

  播放段落

  Example 5
  ::例5

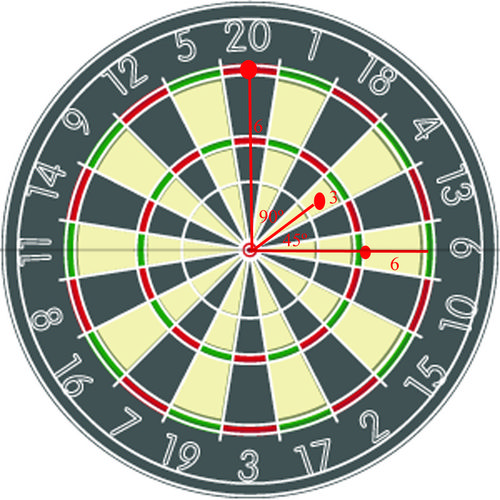
  播放段落

  While playing a game of darts with your friend, you decide to see if you can plot the coordinates of where your darts land. The dartboard looks like this:
  ::在与朋友玩飞镖游戏时,你决定看能不能绘制飞镖降落位置的坐标。

  

  播放段落

  Solution:
  ::解决方案 :

  播放段落

  Since you have the positions of the darts on the board with both the distance from the origin and the angle they make with the horizontal, you can describe them using polar coordinates:  $\begin{align*}\left(4, 0^\circ\right), \left( 3,45^\circ \right), \text{ and } \left(6, 90^\circ \right)\end{align*}$ .  
  ::由于您在板上的位置与飞镖的起源距离和与水平角的距离相同,您可以用极坐标(4,0)、(3,45)和(6,90)来描述它们。

  播放段落

  Summary
  ::摘要

  播放段落
  • The polar coordinate system is a circular system used to visualize and plot angles.
    ::极地坐标系统是一个循环系统,用于可视化和绘图角度。
  播放段落
  • Coordinates in the polar system come in the form  $\begin{align*}(r, \theta),\end{align*}$  where  $\begin{align*}r\end{align*}$  is the polar radius and  $\begin{align*}\theta \end{align*}$  represents the number of degrees or radians from the polar axis.
    ::极地系统中的坐标以(r,)形式出现,其中r为极半径,代表极地轴的度或弧度数。

  播放段落

  Review
  ::回顾

  播放段落
  1. Why can a point on the plane not be labeled using a unique ordered pair $\begin{align*}(r, \theta)\end{align*}$ ?
     ::为何不能使用独家订货对(r,__________________________________________________________________________________________________________________%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
  播放段落
  2. Explain how to graph $\begin{align*}(r, \theta)\end{align*}$ if $\begin{align*}r < 0\end{align*}$ and/or $\begin{align*}\theta > 360\end{align*}$ ^° .
     ::解释如果 r < 0 和/或 360°, 如何绘制图(r, ) 。

  播放段落

  Graph each point on the polar plane:
  ::极平面上的每个点图 :

  播放段落
  3. A $\begin{align*}(6, 145^\circ)\end{align*}$
     ::A (6,145)
  播放段落
  4. B $\begin{align*}\left(-2, \frac{13\pi}{6} \right)\end{align*}$
     :B-2,136)
  播放段落
  5. C $\begin{align*}\left(\frac{7}{4}, -210^\circ\right)\end{align*}$
     ::C(74,-210)
  播放段落
  6. D $\begin{align*}\left(5, \frac{\pi}{2}\right)\end{align*}$
     ::D(52美元)
  播放段落
  7. E $\begin{align*}\left(3.5, \frac{-\pi}{8}\right)\end{align*}$
     ::E(3.5,8)

  播放段落

  Name two other pairs of polar coordinates for each point:
  ::每点指定另外两对极坐标:

  8. $\begin{align*}(1.5, 170^\circ)\end{align*}$
  9. $\begin{align*}\left(-5, -\frac{\pi}{3}\right)\end{align*}$
  10. $\begin{align*}(3, 305^\circ)\end{align*}$
  11. $\begin{align*}\left(4, -\frac{5\pi}{6}\right)\end{align*}$  

  播放段落
  12. Suppose you are traveling north in a boat. A heavy wind moves the boat 15° west of north while traveling 500 m. What is the polar coordinate point that best represents this situation?
      ::假设你正乘船向北航行。大风在北纬15度以西行驶,在500米处行驶。 最能代表这种情况的极地坐标点是什么?
  播放段落
  13. Graph the polar coordinate point from 12 above. 
      ::从上面12处绘制极地坐标点图。
  播放段落
  14. The planets move in a circular motion around the sun. The planet Mercury travels around the sun in an elliptical orbit given by  $$\begin{align*}r=\frac{34,\!420,\!000}{1-0.206\cos\theta},\end{align*}$$ where $\begin{align*}r\end{align*}$  is measured in miles, and the sun is at the pole. Determine the polar radius for the following $\begin{align*}\theta\end{align*}$  values:
      1. $\begin{align*}30^\circ\end{align*}$  
      2. $\begin{align*}-60^\circ\end{align*}$  
      3. $\begin{align*}135^\circ\end{align*}$    
      
      ::行星在太阳周围环绕着圆形运动。 行星“ 水星” 环绕太阳运行, 以 r=34, 420, 420, 1- 0. 206 cos, r 以英里计, 太阳在极上。 确定以下值的极半径 : 30 - 60 - 135
  播放段落
  15. Determine the polar coordinate points for parts a-c from number 14.
      ::确定14号A-c部分的极地坐标点。
  播放段落
  16. Graph the polar coordinate points from 14 above. 
      ::从上面14处绘制极地坐标点图。

  播放段落

  Review   (Answers)
  ::回顾(答复)

  播放段落

  Please see the Appendix.
  ::请参看附录。