9.1 开普勒法律

Section outline

• Select section General

  Collapse Expand

  General

  Collapse all Expand all

  • Select activity 新闻通告

    

    新闻通告 Forum
• Select section 开普勒法律

  Collapse Expand

  开普勒法律

  播放段落

  Much of our real scientific understanding about the solar system began when the Renaissance astronomer  (1473 - 1543) promoted the novel idea that the Earth was not the center of the universe. Instead, the Earth and other planets orbited the Sun, and other stars appeared as fixed points on the celestial sphere.
  
  ::我们对于太阳系的真正科学理解大多始于文艺复兴天文学家(1473 - 1543 ) ( 1473 - 1543 ) ( 1473 - 1543 ) ( 1473 - 1543 ) ( 1473 - 1543 ) ( 1473 - 1543 ) ( 1473 - 1543 ) ) ( “ 地球不是宇宙的中心 ” ) 的新理念。 相反,地球和其他行星绕着太阳运行,其他恒星作为天球的定点出现。

  

  播放段落

  Copernican heliocentrism: the known planets (Mercury, Venus, Earth, Mars, Jupiter and Saturn) orbit the Sun with the fixed stars placed on the celestial sphere. How many planets did Copernicus know about in our solar system? What was the name of the Earth in his diagram?
  ::哥白尼在太阳系中知道多少行星?在他的图表中,地球的名称是什么?

  播放段落

  While many intellectuals in the mid 1500s quietly agreed with the Copernican view, Danish astronomer (1546 - 1601) was a formidable opponent.  Tycho was known for his scrupulous measurements of the positions of planets in our solar system, and he had an agenda: he expected to prove that the Ptolomaic m was correct: the Sun orbited the Earth in a circular path and the other planets executed complicated epicyclic motions as they danced around the Earth. To his immense frustration, Tycho's belief was never supported by the data, and upon his death his assistant and eventual successor,  (1571 - 1630), used Tycho's data to prove that Copernicus was correct: the planets all orbited the Sun.
  
  ::虽然许多知识分子在1500年代中期静静地同意Copernican的观点,但丹麦天文学家(1546 - 1601)是一个强大的对手。Tycho以对太阳系行星位置的精确测量而著称,他有一个议程:他期望证明Ptolomaic mm是正确的:太阳环绕地球环绕着地球,而其他行星则在绕地球跳舞时执行复杂的周期性运动。由于Tycho巨大的挫折感,他的信念从未得到数据的支持,在他去世时,他的助手和最终继承人(1571 - 1630)利用Tycho的数据来证明Copenicus是正确的:所有行星都绕着太阳运行。

  播放段落

    The TYCHO catalog
  
  ::TYCHO TYCHO 目录目录

  The European Space Agency compiled the precise positions and motions of 2.5 Million stars and named the in honor of Tycho Brahe.
  

  播放段落

  Kepler was a religious man who believed in the intrinsic beauty and mathematical perfection of a universe created by God.  Since circular orbits represented a mathematical ideal, Kepler initially assumed that planetary orbits in the solar system would be exactly circular. To his credit, he was able to reconsider this belief when the data better supported an elliptical orbit, for the orbit of Mars was better described by a ellipse than by a circle. Using Tycho Brahe's data, Kepler established three important laws for understanding the motion of planets in our solar system.
  ::开普勒是一个相信上帝所创造的宇宙内在美和数学完美的宗教人士。由于环绕轨道代表着一个数学理想,开普勒最初假设太阳系中的行星轨道完全是环绕的。 值得称赞的是,当数据更好地支持椭圆轨道时,他能够重新考虑这一信念,因为火星轨道比圆圈更能用椭圆来描述。 开普勒利用Tycho Brahe的数据建立了三项重要的法律来理解太阳系中的行星运动。

  播放段落

  Kepler's Laws
  ::开普勒法律

  播放段落
  1. Planets move in ellipses with the Sun at the focus of the ellipse.  
     ::行星以椭圆形式移动,太阳在椭圆的焦点处。
  播放段落
  2. Planets sweep out equal areas in equal time intervals.
     ::行星在同等时间间隔内将平等区域扫出。
  播放段落
  3. The square of the orbital period is proportional to the cube of the semi-major axis.
     ::轨道周期的方形与半主轴的立方体成正比。

  播放段落

  Kepler's First Law
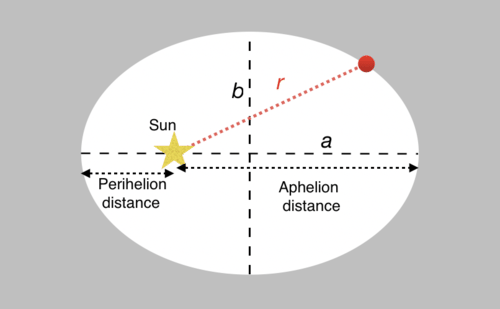
  ::开普勒第一法

  播放段落

  Kepler's first law simply says that planetary orbits are elliptical and that the Sun is at the focus of the ellipse. In the mathematical description of an ellipse, the distance from the center of the ellipse to the widest part of the ellipse is the semi-major axis , $\begin{align*}a\end{align*}$ , and the distance from the center to the narrowest side of the ellipse defines the semi-minor axis , $\begin{align*}b\end{align*}$ . So at its widest point, the ellipse has a diameter of $\begin{align*}2a\end{align*}$ and the narrowest dimension is  $\begin{align*}2b.\end{align*}$   A circle is a special type of ellipse with a radius such that  $\begin{align*}a=b\end{align*}$ .
  ::开普勒的第一部法律只是简单地说行星轨道是椭圆轨道,太阳是椭圆的焦点。在对椭圆的数学描述中,从椭圆中心到椭圆最宽部分的距离是半主轴(a)和从中到椭圆最窄侧的距离(b)。在最宽的点上,椭圆的直径为2a,最窄的尺寸为2b。圆是一个特殊的椭圆类型,其半径为a=b。

  播放段落

  In the Figure below, the semi-major and semi-minor axes of a diagram representing an elliptical orbit are labeled. The Sun is at the focus of the ellipse and the distance between the Sun and the planet (the red dashed line) will change throughout the orbit. There are two special points in the orbit along the semi-major axes: perihelion is the point in the elliptical orbit where the planet makes its closest approach to the Sun, and aphelion is the point in the orbit where the planet is farthest away.
  ::在下图中,代表椭圆轨道的图的半主轴和半小轴标有标签。太阳处于椭圆的焦点,太阳与行星之间的距离(红色破折线)将在整个轨道上发生变化。在半主轴的轨道上有两个特殊点:近视线是地球接近太阳的椭圆轨道上的一个点,远距地球的轨道上有一个点。

  

  播放段落

  Elliptical Orbit: The star is at the focus of the ellipse. The semi-major axis and the semi-minor axis are labeled ``a'' and ``b'' respectively and perihelion and aphelion distances are shown. In an elliptical orbit, the distance between the star and planet changes. At what point is the planet closest to the star? At what point is the planet farthest away from the star?
  ::椭圆轨道 : 恒星位于椭圆的焦点。 半主轴和半minor轴分别标为“ a' ” 和“ b' ” , 并显示近距离和远距离。 在椭圆轨道上, 恒星与行星之间的距离会发生变化 。 行星与恒星的距离在哪个点上? 行星距离恒星最远的地方是哪个点?

   

  播放段落

  The distance between a star and planet, $\begin{align*}r\end{align*}$ ,  is given by the following expression, where  $\begin{align*}a\end{align*}$   is the semi-major axis,  $\begin{align*}e\end{align*}$  is the orbital eccentricity, and $\begin{align*}\theta \end{align*}$   is the angle starting as zero at perihelion and sweeping around the orbit:
  ::恒星与行星之间的距离, r, 由以下表达式表示, 其中一个半主轴是轨道偏心轴, e 是轨道偏心轴, 是以零开始的近地点角, 并环绕轨道 :

  播放段落

                                             $\begin{align*}r=\frac{a\left(1-{e}^{2}\right)}{1+e\cos{\theta}}\end{align*}$              [Eqn 1]
  ::r=a(1-e2)1+ecos__[第1款]

  播放段落

  By definition, the planet will be at perihelion when  $\begin{align*}\theta=0\end{align*}$ and the planet will be at aphelion when $\begin{align*}\theta=\pi \end{align*}$ and those distances can be calculated from the equation above:
  ::根据定义,地球将处于边缘,当 +%0 时,地球将处于边缘,当 +% 时,地球将处于胎儿,这些距离可以从以上方程式中计算出来:

  播放段落

                                                $\begin{align*}{r}_{perihelion}=a\left(1-e\right)\end{align*}$      [Eqn 2]
  ::[Eqn 2] [Eqn 2]

  播放段落

                                           $\begin{align*}{r}_{aphelion}=a\left(1+e\right)\end{align*}$           [Eqn 3]
  ::e) [Eqn 3]

  播放段落

  The distance between the center of the ellipse and the focus of the ellipse is $\begin{align*}ae\end{align*}$ .
  ::椭圆的中心与椭圆的焦点之间的距离是Ae。

  播放段落

  Kepler's Second Law
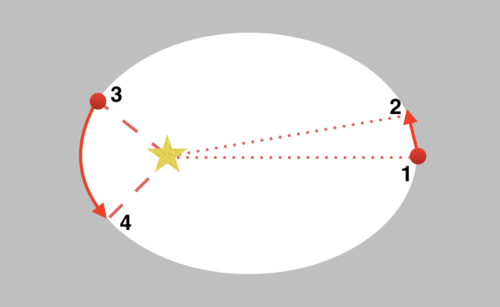
  ::开普勒的第二法

  播放段落

  Kepler's Second Law says that a planet will sweep out equal areas in an orbit in equal time intervals (  below).  Note that the planet does NOT sweep out equal angles in equal time intervals unless the orbit is a circle. In the Figure below, the triangular area defined by the star and points 1 and 2 has an area equal to the area defined by the star and points 3 and 4.
  ::Kepler的《第二法律》指出,一个行星将在一个轨道上以相同时间间隔(以下)清除平等区域。请注意,除非轨道是一个圆圈,否则这个行星不会在相同时间间隔内清除平等角度。在下图中,恒星定义的三角区域以及第1点和第2点的三角区域与恒星定义的区域和第3点和第4点的面积相等。

  播放段落

  Kepler's second law has important implications.  Clearly the distance between points 1 and 2 is shorter than the distance between points 3 and 4 in the Figure below.  Since the time interval is the same for these different distances, the planet is traveling at different velocities.
  ::开普勒的第二定律具有重要影响。 显然,一点和二点之间的距离比下图中三点和四点之间的距离要短。 由于这些不同距离的时间间隔相同,这个星球正在以不同速度运行。

  

  播放段落

  Kepler's Second Law: The planet sweeps out equal areas in equal time intervals. The time that it takes the planet to travel from point 1 to point 2 is equal to the time to orbit from point 3 to point 4, even though those distances are not equal. Is the planet traveling fastest at apastron or periastron?
  ::开普勒的第二定律 : 行星在相等时间间隔内扫出相等的区域。 它从1点到2点的飞行时间相当于从3点到4点的轨道时间, 尽管这些距离并不相等 。 行星在开普勒的开普勒的第二定律中行走最快的行星是在开普斯顿或远地点行走的吗 ?

  播放段落

  The velocity of a planet relative to the host star is derived by equating the gravitational force to the orbital acceleration. This velocity, $\begin{align*}v\end{align*}$ , is given by the vis-viva equation 4:
  ::行星相对于宿主恒星的速度通过将引力与轨道加速度等同而得出。

  播放段落

                              $\begin{align*}v=\sqrt{GM\left(\frac{2}{r}-\frac{1}{a}\right)}\end{align*}$                   [Eqn 4]
  ::vGM(2r-1a) [Eqn 4]

  播放段落

  where G is the gravitational constant:  $\begin{align*}G=6.67408\times {10}^{-11}{m}^{3}{kg}^{-1}{s}^{-2}\end{align*}$ ,
  ::其中G是引力常数:G=6.67408×10-11m3kg-1-s-2;

  播放段落

  $\begin{align*}r\end{align*}$ is the distance between the star and the planet,
  ::r 是恒星与行星之间的距离,

  播放段落

  and $\begin{align*}a\end{align*}$ is the semi-major axis of the elliptical orbit.
  ::a 是椭圆轨道的半主轴。

  播放段落

  The velocity of the planet in its orbit can easily be calculated at perihelion (or aphelion) by substituting the expression for r _perihelion (or r _aphelion ) into the vis-viva equation. In the case of a circular orbit, $\begin{align*}r=a\end{align*}$ , and the velocity of a planet in a gravitationally bound orbit is constant and simplifies to:
  ::地球在其轨道上的速度可以很容易地在近地点(或远地点)计算,办法是用正幸存者方程中表示的雷贝里翁(或正幸存者方程)来代替。

  播放段落

                                                   $\begin{align*}v=\sqrt{\frac{GM}{R}}\end{align*}$            [Eqn 5]
  ::五、GMR [Eqn 5]

  播放段落

  where $\begin{align*}R\end{align*}$ is the radius of the circular orbit.
  ::R是圆形轨道的半径。

  播放段落

   Kepler's Third Law
  ::开普勒第三法律

  播放段落

  About a decade after Kepler had formulated his first two rules for the motion of planets in the solar system, he published a third law based on his empirical data, which says that the square of the orbital period is proportional to the cube of the semi-major axis:
  ::Kepler为太阳系行星运动制定了头两条规则之后大约十年,他根据经验数据发布了第三种法律,其中规定轨道周期的平方与半主轴的立方成正比:

  播放段落

                                                      $\begin{align*}{P}^{2}\propto{a}^{3}\end{align*}$                [Eqn 6]
  ::P2a3 [Eqn 6]

  播放段落

  where  $\begin{align*}a\end{align*}$   is  the semi-major axis of the elliptical orbit and $\begin{align*}P\end{align*}$  is the orbital period.
  ::a 为椭圆轨道的半主轴,P为轨道周期。

  播放段落

  This means that a planet that is closer to the Sun has a shorter orbital period than a planet that orbits farther away. Mercury completes one orbit in 88 days, Venus orbits in 225 days, and the Earth takes 365 days to travel around the Sun.
  
  ::这意味着接近太阳的行星的轨道周期短于轨道运行距离更远的行星。 汞在88天内完成一个轨道,金星轨道在225天内完成,地球绕太阳飞行需要365天。

  播放段落

  Kepler's third law can be used to find the orbital period or semi-major axis for planets in our solar system by dividing each side of equation 5.1.6 with values for the Earth.
  ::开普勒的第三项法律可以用来找出太阳系行星的轨道周期或半主轴,将方程5.1.6的两侧除以地球的数值。

  播放段落

                                   $\begin{align*}{\left(\frac{{P}_{Jup}}{{P}_{Earth}}\right)}^{2}={\left({\frac{{a}_{Jup}}{{a}_{Earth}}}\right)}^{3}\end{align*}$         [Eqn 7]
  
  :PJupPEarth)2=(aJupaEarth)3 [Eqn 7]

  播放段落

  The Earth has a 1 year orbital period and a semi-major axis defined as 1 (1 AU). Using those same dimensional units (years and AU) we can calculate the orbital period of Jupiter, which has a semi-major axis of 5.2 AU:
  ::地球的轨道周期为1年,半主轴为1(1个非盟),使用相同的维单位(年份和非盟),我们可以计算木星的轨道周期,木星的半主轴为5.2个非盟:

  播放段落

                                   $\begin{align*}{\left(\frac{{P}_{Jup}}{1\,year}\right)}^{2}={\left({\frac{{a}_{Jup}}{1\,AU}}\right)}^{3}\end{align*}$          [Eqn 8]
  :1岁)2=(ajup1AU)3 [项目8]

  播放段落

  $\begin{align*}{P}_{Jup}=11.86\,years\end{align*}$  
  
  ::PJup=11.86岁