9.2 双体问题

Section outline

• Select section General

  Collapse Expand

  General

  Collapse all Expand all

  • Select activity 新闻通告

    

    新闻通告 Forum
• Select section 双体问题

  Collapse Expand

  双体问题

  播放段落

  The meaning behind Kepler's third law
  ::开普勒第三法律的含义

  播放段落

  Kepler used Tycho's measurements of the planet positions over time to empirically derive the mathematical relationship captured in Kepler's third law. However, Kepler did not have a physical explanation for why the planets orbited the Sun. This is a good example of how science works. We make observations, try to fit the observations with a mathematical model, and then look for an elegant generalization that is both descriptive and predictive. If the mathematical generalization holds up under intense scrutiny, it is elevated to have the status of a theory.
  ::Kepler用Tycho对地球位置的测量方法,用时间来从经验上得出Kepler第三定律所捕捉的数学关系。 但是, Kepler并没有从物理上解释行星绕太阳运行的原因。 这是科学如何运作的一个很好的例子。 我们进行观察, 尝试用数学模型来匹配观测结果, 然后寻找一种既描述性又具有预测性的优雅的概括化。 如果数学的概括化在严密的检查下持续, 它被提升到具有理论的地位 。

  播放段落

  About sixty years after Kepler published his third law for how the motion of planets in our solar system behaved, Isaac Newton (1643 - 1727) helped us to understand the "why." Newton developed a mathematical description of gravity as a force between two particles that is proportional to the product of the particle masses ( $\begin{array}{r}{M}_1\end{array}$ and $\begin{array}{r}{M}_2\end{array}$ ) and inversely proportional to the square of the distance, $\begin{array}{r}d\end{array}$ , between them:
  ::开普勒发表了关于太阳系中行星运动的第三部法律(Isaac Newton (1643 - 1727)) 约60年后, 牛顿(1643 - 1727)帮助我们理解“为什么 ” 。 牛顿开发了一个“引力”数学描述,称重力是两个粒子之间的一种力量,与粒子质量(M1和M2)的产物成正比,与它们之间的距离平方成反比:

  播放段落

                                                              $\begin{array}{r}{F}_g=\frac{G{M}_1{M}_2}{d^2}\end{array}$        [Eqn 1]
  ::Fg=GM1M2d2 [Eqn 1]

  播放段落

          where the constant of proportionality is $\begin{array}{r}G=6.67408\times {10}^{-11}{m}^3{kg}^{-1}{s}^{-2}\end{array}$ .
  ::相称性不变值为G=6.67408×10-11m3kg-1-s-2。

  播放段落

  Newton's laws for forces
  ::牛顿的军队法

  播放段落
  1. Unless acted on by an unopposed force, bodies at rest stay at rest, and bodies in motion stay in motion.
     ::除非由一支无对立力量采取行动,否则休息机构应休息,活动机构应保持活动状态。
  播放段落
  2. The vector sum of forces is equal to mass times the vector acceleration: $\begin{array}{r}\sum \stackrel{\to }{F}=m\stackrel{\to }{a}\end{array}$  
     ::矢量的矢量总和等于矢量加速度的质量乘以:Fma
  播放段落
  3. For every action, there is an equal and opposite reaction.
     ::对于每一项行动,都有平等和相反的反应。

   

  播放段落

  From first principles, Newton was able to show that the orbits of planets around the Sun could be described by a gravitational force. Starting with Newton's second law, $\begin{array}{r}F=ma\end{array}$ , and using the definition of , $\begin{array}{r}a=\frac{v^2}{a_{rel}}\end{array}$ where  $\begin{array}{r}{a}_{rel}\end{array}$ is the orbital radius, or the distance between the star and planet, 
  ::从最初的原则来看,牛顿能够显示,太阳周围行星的轨道可以用引力来描述。从牛顿的第二定律F=ma开始,并使用a=v2arel的定义,a=v2arel,在这种定义中,srel是轨道半径,或恒星与行星之间的距离,

  播放段落

                                    $\begin{array}{r}{F}_G=\frac{G{M}_{\odot }{m}_{planet}}{{a_{rel}}^2}=m_{planet}\frac{v^2}{a_{rel}}\end{array}$       [Eqn 2]
  ::FG=GMmplanetarel2=mplanetev2arel [英吋2]

  播放段落

                                                       $\begin{array}{r}\frac{G{M}_{\odot }}{a_{rel}}=v^2\end{array}$                   [Eqn 3]
  ::GMarel=v2 [项目3]

  播放段落

          where $\begin{array}{r}{M}_{\odot }\end{array}$ is the mass of the Sun ( $\begin{array}{r}1.989\times {10}^{30}kg\end{array}$ ) and $\begin{array}{r}v\end{array}$ is the velocity of the planet.
  ::M是太阳的质量(1.989×1030千克),V是行星的速度。

  播放段落

  The orbital period, $\begin{array}{r}P\end{array}$ , of the planet is the distance that the planet travels around the circular orbit divided by velocity (check and you'll see that distance / velocity has units of time, appropriate for an orbital period):
  ::行星的轨道周期,P,是行星环绕圆形轨道运行的距离,以速度除以速度(检查和你会看到距离/速度有时间单位,适合轨道周期):

  播放段落

                                            $\begin{array}{r}P=\frac{2\pi a_{rel}}{v}=\frac{2\pi a_{rel}}{\sqrt{\frac{G{M}_{\odot }}{a_{rel}}}}\end{array}$            [Eqn 4]
  ::P=2arelv=2arelgMarel[第4款]

  播放段落

                                                  $\begin{array}{r}{P}^2=\left(\frac{4{\pi }^2}{G}\right)\frac{{a_{rel}}^3}{M_{\odot }}\end{array}$            [Eqn 5]
  ::P2 = (42G) arel3M [Eqn 5]

  播放段落

  This is Newton's version of Kepler's third law: the square of the orbital period is proportional to the cube of the semi-major axis. With Newton's version of this law, we are no longer limited to describing the motion of planets in the solar system.  We can change the mass of the star to find a new constant of proportionality between orbital period, $\begin{array}{r}P\end{array}$ , and the semi-major axis, $\begin{array}{r}{a}_{rel}\end{array}$  in the equations above, in other exoplanet systems.
  ::这是牛顿版本的开普勒第三法律: 轨道周期的方块与半主轴的立方体成比例。 根据牛顿版本的这一法律, 我们不再局限于描述太阳系中的行星运动。 我们可以改变恒星的质量, 以在轨道周期( P) 和半主轴( 半主轴) 之间找到一个新的相称性常数, 在以上等式中, 在其他外板系统中, 以 P 为单位 。

  播放段落

  As with Kepler's third law in the previous section, we can define convenient units to make this calculation easier.  By definition, the orbit of the Earth is 1 year, and the average distance between the Sun and the Earth (the semi-major axis of the Earth's orbit) is 1 Astronomical Unit (1 AU = 149,597,870,700 km = 92,955,000 miles).  So, if we adopt those same units (period in units of years , semi-major axis in units of AU , and stellar masses in units of of solar masses ), we can make some quick calculations for other planetary systems.  After dividing both sides of equation 4.2.5 by the values for our solar system, the constants will cancel out, leaving an easy and useful equation (the required dimensions are in square brackets):
  
  ::根据定义,地球轨道为1年,太阳与地球(地球轨道的半主轴)的平均距离为1天文单位(1AU=149,597,870,700公里=92,955,000英里)。因此,如果我们采用同样的单位(年数单位、非盟单位的半主轴和太阳质量单位的星团),我们可以为其他行星系统做一些快速的计算。在将方程式4.2.5两侧除以太阳系的值之后,常数将取消,留下一个简单和有用的方程(所需方位置于方括号内):

  播放段落

                                                $\begin{array}{r}{P}^2\left[yr\right]=\frac{{a_{rel}}^3\left[AU\right]}{M\left[M_{\odot }\right]}\end{array}$             [Eqn 6]
  ::P2[yr]=arel3[AU]M[M][Eqn 6]

  播放段落

    EXAMPLE
  ::特例

  播放段落

  A star that is 0.5 times the mass of the Sun has a planet in a 730.5 day orbit.  What is the semi-major axis of the orbit?
  ::太阳质量0.5倍的恒星在730.5天轨道上有一个行星。轨道的半主轴是什么?

  播放段落

  First, change the period from days into years: 730.5 d = 2 yr.
  ::首先,将期限从几天改为几年:730.5天=2年。

  播放段落

  Then, $\begin{array}{r}{a}_{rel}={\left(0.5\times 2^2\right)}^{1/3}=1.26\end{array}$ Astronomical Units (AU).
  ::然后,是(0.5x22)1/3=1.26天文单位(AU)。

  播放段落

  Frame of reference
  ::参考框架

  播放段落

  So far, we've assumed a simplification: we have been working in the frame of reference of the Sun.  There is nothing wrong with this, we just have to understand that in this reference frame, the Sun is not moving - the planets orbit the Sun and the elliptical orbit has semi-major axes for the planets that are relative to the Sun. However, Newton's third law tells us that while the Sun exerts a gravitational force on a planet, that planet also exerts a gravitational force on the Sun. The planets cause the Sun to wobble in an orbit about a common center of mass. 
  ::到目前为止,我们已经假设了一个简化: 我们一直在太阳的参照框架里工作。 这一点没有错, 我们只需要理解, 在这个参照框架里,太阳并没有移动, 行星环绕太阳和椭圆轨道的行星有相对太阳的行星的半主轴。 但是, 牛顿的第三个法律告诉我们, 当太阳在行星上施加引力时, 行星也在太阳上施加引力。 行星使太阳在一个共同的物体中心轨道上起伏。

  播放段落

  Let's begin with the classic 2-body problem: a star is orbited by a single planet. Later, we'll discuss what happens when there are  $\begin{array}{r}N\end{array}$  bodies orbiting the star. In the 2-body problem, we change our reference frame from the star to the center of mass. The (COM) is a point along a line that connects two objects (for the discussion here, the two objects are a star and planet) such that:
  ::让我们从典型的 2 体问题开始: 恒星由单个行星环绕轨道运行。 稍后, 我们将讨论当有 N 体物体环绕恒星运行时会发生什么。 在 2 体问题中, 我们把参照框从恒星更改为质量中心。 (COM) 是一条连接两个天体( 这里的讨论, 两个天体是恒星和行星)的线条上的点 , 因此 :

  播放段落

                                                 $\begin{array}{r}{M}_{\ast }{r}_{\ast }=m_{planet}{r}_{planet}\end{array}$            [Eqn 7]
  ::M*rmplaneterplanenet[第7项]

  播放段落

  The star is located a distance $\begin{array}{r}{r}_{\ast }\end{array}$ away and orbits the COM. The planet also orbits the COM, but at a larger distance (since it is universally true that $\begin{array}{r}{M}_{\ast }>m_{planet}\end{array}$ then it is also always true that $\begin{array}{r}{r}_{planet}>R_{\ast }\end{array}$ ).  In the COM frame, it is the center of mass that is stationary. The below depicts the motion of the star and planet relative to the COM. Notice that at any point in the orbit a line can be drawn from the star through the COM to the planet.
  ::恒星位于远处,绕着恒星运行。 行星也绕着恒星运行, 但距离更远( 因为一般情况下, Mmplanet 和 rplanet>R* 都是正确的。 在 COM 框中, 质量中心是静止的。 下面描述恒星和行星相对于 COM 的动态。 请注意, 在轨道的任何点上, 一条线可以从恒星通过 COM 到行星。

   

   

  播放段落

  For some of the detection techniques (the Doppler method and astrometry) that we discuss in the next chapter, we measure the orbital motion of the star and infer the presence of an unseen planet. Therefore, the equations for those techniques are developed in the COM frame - it is the motion of the star that betrays the existence of an orbiting planet.  For other techniques (direct imaging and transits) the motion of the star does not provide any useful information, and we can simplify our analysis by working in the frame of reference of the star and studying the motion of the planet relative to the "stationary" star.
  ::对于我们在下一章讨论的一些探测技术(多普勒方法和天体测量),我们测量了恒星的轨道运动,并推断了一个看不见的行星的存在。因此,这些技术的方程式是在COM框架中开发的,就是恒星的动作暴露了轨道行星的存在。对于其他技术(直接成像和中转)来说,恒星的运动没有提供任何有用的信息,我们可以通过在恒星参照框架内工作,研究行星相对于“静止”恒星的运动来简化我们的分析。

  播放段落

  You intuitively switch back and forth between reference frames in real life. Like Tycho, we picture the Sun rising and setting, when in fact the Earth is spinning on its axis once every 24 hours. For most things that we do, a geocentric reference frame works just fine. But if we want to understand when Jupiter will be seen in the night sky, we need to switch to the Copernican heliocentric reference frame. All reference frames (if treated correctly) are equally valid; some reference frames are just easier for solving certain problems.
  ::你直觉地在现实生活中的参照框架之间互换。像Tycho一样,我们想象太阳的升起和落成,事实上地球每24小时在其轴上旋转一次。对于我们所做的大多数事情来说,一个以地球为中心的参照框架效果很好。但如果我们想了解木星何时会在夜空中出现,我们需要切换到Copernican 太阳中心参照框架。所有参照框架(如果正确处理的话)都同样有效;有些参照框架只是比较容易解决某些问题。

  播放段落

  Orbital orientations are 3-dimensional
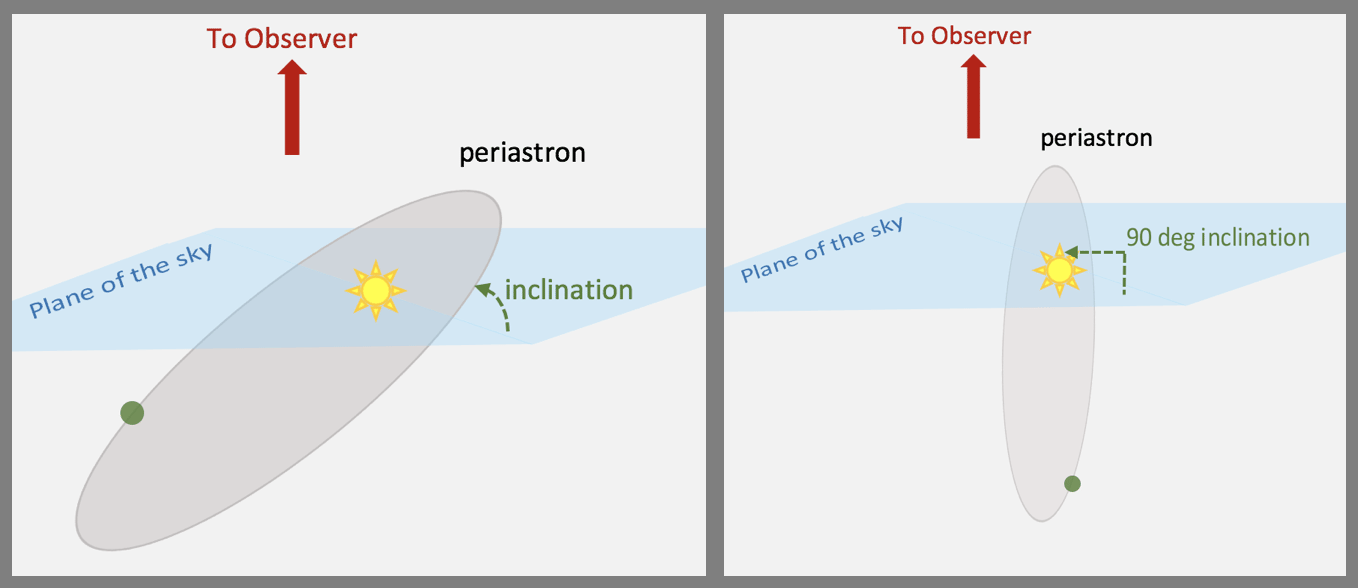
  ::轨道方向为三维

  播放段落

  The fundamental plane of an orbit can be sketched on a piece of paper; to a reasonable approximation, it is flat (like the Figures showing elliptical orbits in the previous section) and can be thought of as having a 2-dimensional shape. However, the situation is more complex because orbits are randomly oriented in the 3-d volume of space, as shown in the  below.  From our view, the randomly oriented orbit is then projected back onto the plane of the sky with a 2-d shape that is different from the true fundamental plane orbit. 
  ::轨道的基本平面可以在一张纸上绘制;对于合理的近似值来说,它是平的(如前一节中显示椭圆轨道的数字),可以被视为具有二维形状。然而,情况更加复杂,因为轨道在3D空间体积中随机定向,如下文所示。从我们的角度看,随机定向轨道然后被投射回天空平面,其2D形状不同于真正的基本平面轨道。

  播放段落

  Imagine a circular orbit as a hula hoop.  If orientation of this hula-hoop orbit is face-on to your line of site, then you see the full 2-d circular orbit projected as a circle onto the plane of the sky. If the orientation is edge-on, then you would see the orbit projected as a line.  And if the orbit is inclined by some arbitrary angle (say 45 degrees) then the 2-d circular orbit would be projected as an ellipse. The time stamp on each observation allows astronomers to distinguish projection effects from the true orbital eccentricity. 
  ::想象一个圆形轨道作为 hula 环形轨道。 如果这个 hula-hoop 轨道的定向是直线对准您所在的站点, 那么您就会看到整个 2 - 2 环形轨道是投向天空平面的圆形。 如果方向是边缘, 那么您就会看到一个圆形轨道是直线。 如果轨道被某些任意角度( 45 度) 倾斜, 那么2 - 2 环形轨道就会被投射为椭圆。 每次观测的时间戳都允许天文学家区分投影效果和真正的轨道偏心。

  

  播放段落

  Three dimensional orbits are randomly oriented in space, and we view their projection onto the plane of the sky. How will the sky-projected orbit in the frame on the left compare to the sky-projected orbit in the frame on the right?
  ::三维轨道在空间中随机定向,我们看到它们投射到天空的平面上。 左边框的天空预测轨道与右边框的天空预测轨道相比如何?

   

  播放段落

  The N-body problem
  ::N - 身体问题

  播放段落

  When there are more than two objects (i.e., more than just the star and one planet) in a system, the   gravitational interactions of additional   bodies   of "N" objects can perturb the simple Keplerian orbit of a planet. In the    below, there are three objects (N = 3), a star and two planets.   The inner planet will have a shorter orbital period than the outer planet (Kepler's third law). As the inner planet races around its orbital track, it will feel an additional accelerating force (both forward and outward) every time it approaches the outer planet (the outer planet will also feel a small backward and inward force from the inner planet). This situation is reversed after the inner planet passes the outer planet; now the gravity from the outer planet pulls back on the inner planet.   The smaller planet also tugs back on the more massive planet, but with a smaller perturbing effect.
  ::当一个系统中有两个以上的天体(即不止是恒星和一个行星)时,“N”天体中更多物体的引力相互作用会干扰一个行星简单的开普勒轨道。在下面,有三个天体(N=3),一颗恒星和两个行星。内行星的轨道周期将比外行星短(Kepler的第三个定律)。当内行星绕其轨道运行时,每接近外行星,它就会感受到一种额外的加速力(前向和外向) (外向) (外行星也会感受到内行星的后向和内向力量 ) 。 在内行星穿过外行星后,这种情况会逆转;现在外行星的引力会拉回内行星。较小的行星也会在更庞大的行星上拉回,但产生更小的扰动效应。

   

  

   

  播放段落

  When the two planets depicted above make a close approach, they exert a gravitational tug on each other. If one of the orbits is at all non-circular, these episodic gravitational interactions can result in changes in the orbital eccentricity of one or both planets. Why will the planet-planet interactions cancel out for circular orbits, but not for elliptical orbits?
  ::当上面描述的两个行星接近时,它们彼此进行引力拖引。如果其中的一个轨道完全不环绕,这些偶发引力相互作用可能导致一个或两个行星的轨道偏心变化。 为什么行星-行星平面的相互作用会取消环绕轨道,而对于椭圆轨道则不会取消?

  播放段落

  At the level of measurement precision available to Tycho and Kepler, the planets in our solar system seemed to orbit like clockwork. However, even Newton worried that chaotic gravitational interactions between planets might require divine intervention to   .
  ::在Tycho和Kepler掌握的测量精确度水平上,太阳系中的行星似乎像时钟一样运行。 然而,甚至牛顿也担心行星之间混乱的重力相互作用可能需要神的干预。

  播放段落

  Perturbation theory was developed by Lagrange and Laplace to study long range gravitational forces between planets in our solar system. However, the most effective way to understand non-Keplerian interactions in a multi-planet system is to carry out a computer simulation using an N-body code. These simulations treat planets as massive particles with a particular position and velocity, and the Newtonian forces between all objects in the system are integrated to yield a net force at each time step that conserves energy and angular momentum.
  ::Lagrange和Laplace开发了扰动理论,以研究太阳系行星之间的远距离引力。然而,了解多平台系统中非克隆相互作用的最有效方法是使用N-body代码进行计算机模拟。这些模拟将行星作为具有特定位置和速度的大规模粒子对待,而系统中所有物体之间的牛顿力被整合,以在每一个步骤产生净力,节约能源和角动向。

  播放段落

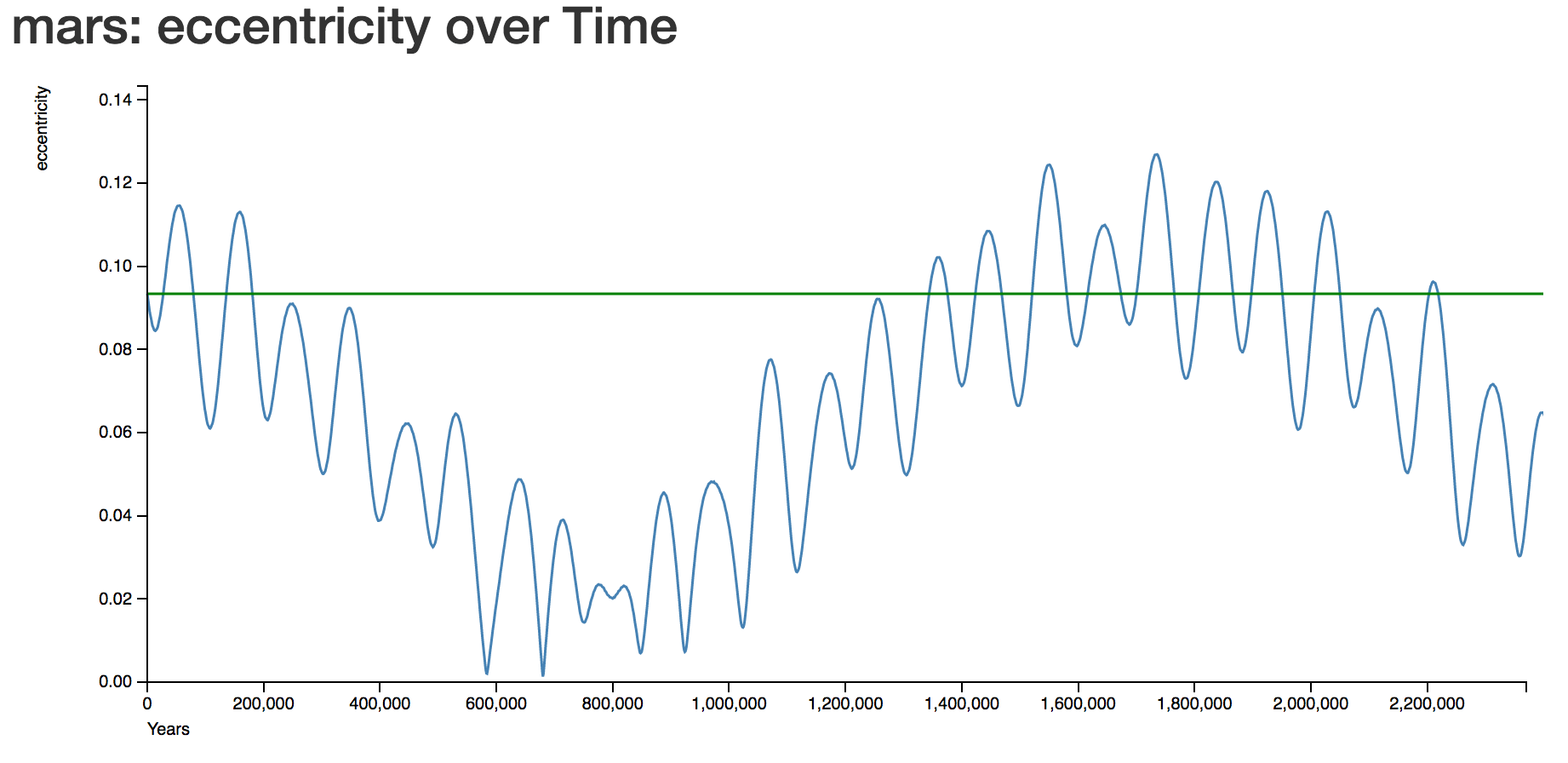
  The non-Keplerian gravitational interactions that take place in our solar system are so small that our planets are considered to be   dynamically stable   for billions of years. The planets stay confined in a small neighborhood around their orbital tracks. However there are changes in eccentricity that occur because of planet-planet interactions.  The   below shows the eccentricity of Mars over a 2 Million year N-body integration of the solar system. 
  ::在太阳系中发生的非克隆引力相互作用如此之小,以至于我们的行星在数十亿年的时间里被认为具有动态稳定。行星被困在轨道周围的小附近。然而,由于行星和行星的相互作用,偏心性发生了变化。下文显示了火星在200万年时间里对太阳系的北体整合的偏心性。

   

  

   

  播放段落

  N-body integration using John Chambers "Mercury" code shows the changes in eccentricity that occur for Mars because of gravitational interactions from other planets in the solar system. By how much does the eccentricity of Mars typically change over 100,000 year time scales? Over 2Myr timescales?
  ::使用约翰·钱伯斯(John Chambers)“Mercury”代码进行N-body集成显示了火星因太阳系其他行星的引力相互作用而发生的偏心变化。火星的偏心变化通常在100,000年的时间尺度上有多大? 超过2Myr的时间尺度?

  播放段落

  If gravitational perturbations between planets are too large, the eccentricity of a planet will increase and the planet may collide with other planets or migrate to a different orbit. In some cases, the planets  could   fall into the star, or be completely ejected from the planetary system.
  ::如果行星之间的引力扰动过大,行星的偏心度就会增加,行星可能与其他行星相撞或迁移到不同的轨道上。 在某些情况下,行星会掉入恒星,或被完全从行星系统中抛出。