Course: 10.3 多普勒技术 | The Way To Learn

The Way To Learn

Section outline

Select section General

Collapse Expand
General

Collapse all Expand all
- Select activity 新闻通告
  
  新闻通告 Forum
Select section 多普勒技术

Collapse Expand
多普勒技术
Indirect detection
::间接检测

The Doppler technique (also called the radial velocity technique) was the first method to successfully detect exoplanets orbiting sun-like stars. This technique measures the velocity of stars over time. The "radial" part of "radial velocity" comes from the fact that only the component of the velocity along our line of sight ("radial") can be measured using the Doppler effect.
::多普勒技术(也称为射线速度技术)是成功探测太阳般恒星轨道外行星的第一个成功方法。该技术测量恒星随时间变化的速度。 “ 射线速度”中的“ 射线”部分来自这样一个事实,即只有我们视线上速度的组成部分( “ 射线” ) 才能使用多普勒效应测量。

All stars are traveling in orbits around the center of our Milky Way galaxy. For example, the Sun takes about 220 Myr to complete one loop around the galaxy. As the Sun travels around the galaxy, some stars appear to be moving toward us while others are moving away.
::所有恒星都在银河系中心周围的轨道上运行。例如,太阳需要大约220米尔来完成星系环绕的一个环环。随着太阳绕星系环绕星系运行,有些恒星似乎正在向我们移动,而另一些恒星则在向着我们移动。

After subtracting the constant galactic velocity for a given star, a residual small periodic wobble in the velocity of a star can reveal that the star is being tugged around a common center of mass by another body, as shown in the below. These residual velocities can be modeled to determine whether the orbiting object is a planet. With the Doppler technique, the planet is never observed (making this an "indirect" detection method). Instead, the time-varying velocity of the host star is modeled to infer the presence of an unseen planet.
::减去恒星的恒星的恒星常数银河速度后,恒星速度中一个微小的周期性波纹,可以揭示恒星正被另一个物体在普通质量中心周围拖拉,如下文所示。这些残余速度可以建模来确定轨道物体是否是一个行星。多普勒技术使行星从未被观测过(使这个“间接”探测方法成为一种“间接”探测方法 ) 。相反,主星的时间变化速度被建模,以推断是否存在一个看不见的行星。

The star and planet orbit a common center of mass. We do not see the planet, but we can measure the radial velocity of the star. Once the stellar velocities for a complete orbit have been mapped out, we can model the data to discover the planet. Why does the Doppler technique only measure the component of the velocity that is projected along our line of site?
::恒星和行星环绕一个共同质量中心。我们看不到行星, 但我们可以测量恒星的辐射速度。一旦绘制出一个完整轨道的恒星速度, 我们就可以模拟数据来发现行星。为什么多普勒技术只测量了我们发射的速度的部件?

To recap: all stars have some nearly constant radial velocity; stars that exhibit a residual periodicity in their radial velocities have a gravitationally bound companion.

::要回顾一下:所有恒星都有一些几乎固定的辐射速度;在辐射速度中呈现剩余周期的恒星有一个引力紧凑的伴星。

How do you measure the velocity of a star?
::你如何测量恒星的速度?

The Doppler technique makes use of the fact that light is a wave and as the source of light (the star) is moving toward us or away from us, the frequency of the light emitted by the star is blue-shifted or red-shifted (by the " "). Doppler shifts are measured from the spectrum of a star, where the stellar flux (the photons of light from the star that are captured by the detector) is sorted into component wavelengths.
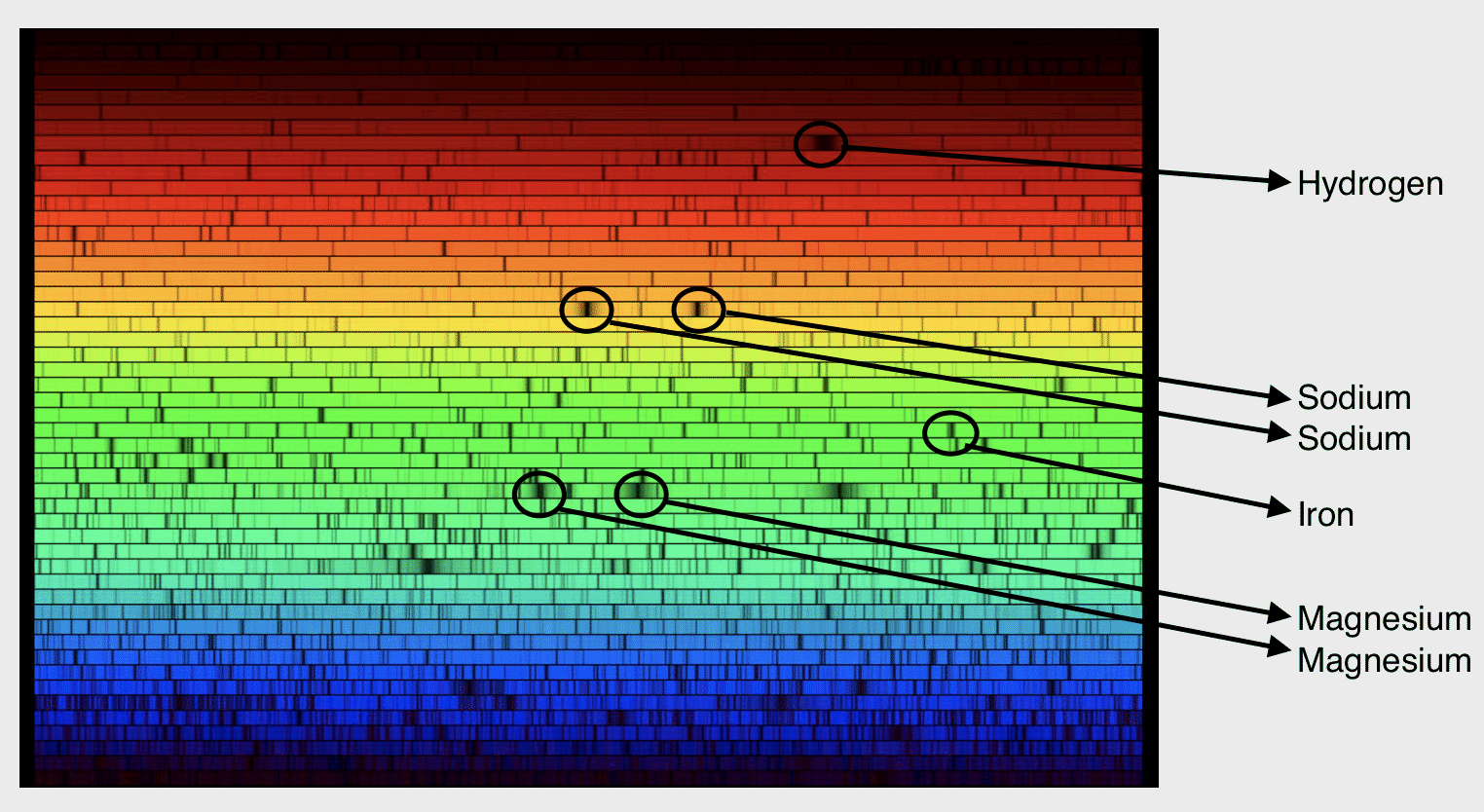
::多普勒技术利用以下事实:光是波,随着光源(恒星)向我们移动或远离我们,恒星发射的光的频率是蓝色的或红色的(由“ ” ) 。多普勒转换是从恒星的频谱中测量的,星际通量(由探测器捕捉的恒星发出的光的光片)被分解成成成成成件波长。

The below shows an ``echelle'' spectrum where the rainbow spectrum of light has been cleverly chopped and stacked by the optics of the instrument (a spectrograph). The spectrum spans the entire visible wavelength range from 400 - 700 nm and each row of the spectrum spans roughly 10 nm. In this spectrum, there are thousands of dark spectral absorption lines corresponding to wavelengths where specific atomic transitions occur (e.g., hydrogen, sodium, iron, and magnesium absorption lines are identified below) and absorb emerging light in the atmosphere of the star.
::以下显示“echelle”的光谱,其中彩虹光谱由仪器的光谱(光谱仪)巧妙地切割和堆叠起来。光谱横跨整个可见波长400-700纳米,每行光谱大约10纳米。在这一光谱中,有数千条与波长相对应的暗光谱吸收线,这些波长是特定原子转换(例如氢、钠、铁和镁吸收线在下面标明)发生的,并吸收恒星大气中出现的光。

An echelle spectrum of the Sun taken with the Fourier Transform Spectrograph at the National Solar Observatory, Kitt Peak, AZ. Each row is about 10 nanometers wide and the orders of the spectrum are stacked from 400 to 700 nm. The dark vertical lines in each row are produced by atomic absorption from different chemical elements. Where are these atoms physically located?
::国家太阳能天文台、Kitt Peak、AZ的Fourier变形光谱仪拍摄了太阳的电极光谱。每行宽约10纳米,频谱的顺序在400至700纳米之间堆叠。每行的暗垂直线是通过不同化学元素的原子吸收产生的。这些原子在哪里?

After the echelle spectrum is recorded with a low noise digital camera, the image is transformed into a more manageable format by extracting each row or order into a series of arrays (an example of this array near the two sodium lines in the echelle image above is shown in the above). Each pixel in the array (sometimes called a 1-d spectrum) contains the stellar flux and the calibrated wavelength of the light.
::在用低噪声数字相机记录电子电子频谱后,图像通过将每一行或顺序提取成一系列阵列(上面显示的是以上电子频谱图象中两条钠线附近的这种阵列的例子)而转化为更易于管理的格式。阵列中的每个像素(有时称为1-d频谱)包含恒星通量和光的校准波长。

The absorption features in a stellar spectrum reveal the composition of the star, but they can also be used to measure the radial velocity of the star. The velocity of the star, $\begin{align*}v\end{align*}$ , can be calculated from the non-relativistic Doppler equation by measuring the wavelength shift for each of the absorption lines:
::恒星谱中的吸收特性揭示了恒星的构成,但它们也可以用来测量恒星的辐射速度。恒星的速度, v 可以通过测量每个吸收线的波长变化,从非相对的多普勒方程中计算出:

                                                $\begin{align*}\frac{\Delta \lambda}{\lambda}=\frac{v}{c}\end{align*}$              [Eqn 1]
::vc [Eqn 1]

where $\begin{align*}\Delta \lambda\end{align*}$ is the average shift measured for thousands of absorption lines,
::其中是数千条吸收线的平均变化量,

$\begin{align*}\lambda\end{align*}$ is the known rest wavelength of each absorption line,
::是已知的每条吸收线的休息波长

$\begin{align*}c\end{align*}$ is the speed of light (299,792,458 m/s).
::c 是光速(299,792,458米/秒)。

A segment of the 1-d extracted spectrum around the deep pair of sodium absorption lines is shown in the image below. A decrease in flux (i.e., an absorption line) occurs wherever there is an atomic transition that absorbs light from the star. In the below, each shift of the spectrum simulates a different velocity shift. By measuring the periodic shift of the wavelengths for these lines ( $\begin{align*}\Delta \lambda\end{align*}$ ) relative to the rest wavelength ( $\begin{align*}\lambda\end{align*}$ , indicated by the red vertical lines for sodium), the velocity of the star over time can be calculated.
::下面的图像显示的是1d提取频谱中围绕深钠吸收线的一段。当原子转换吸收来自恒星的光时,通量(即吸收线)就会下降。在下面,光谱的每一次变化模拟不同的速度变化。通过测量这些线的波长()相对于其余波长()的周期性变化,以钠的红色垂直线为标志,可以计算恒星随时间推移的速度。

The Doppler shift is measured from each spectrum of the star and the time series radial velocities are calculated. Spectra with periodic Doppler shifts can be fit with a Keplerian model that describes the orbital period, planet mass and the shape and orientation of the orbit. How is the velocity of the star determined from the shifting of the atomic absorption lines?
::多普勒变化是从恒星的每个频谱中测量的,并且计算出时间序列的辐射速度。周期性多普勒变化的斯佩克特拉可以与描述轨道周期、行星质量以及轨道形状和方向的开普勒模型相匹配。如何从原子吸收线的移动中确定恒星的速度?

The animation above is an extreme exaggeration (for the purpose of illustration) of the reflex Doppler shift that would occur from orbiting exoplanets. The spectral absorption lines in the animation above are between 5 - 20 pixels in width. A spectral line shift of just one pixel on a detector corresponds to a radial velocity change of about 1000 m/s. The amplitude of Doppler shifts caused by exoplanets would be invisible to the eye on the scale shown above.
::以上动画是(为说明目的)从轨道外行星轨道上发生的反动多普勒移动的极端夸张(为说明目的)。以上动画中的光谱吸收线宽度在5-20像素之间。在探测器上仅一个像素的光谱线移动与大约1000米/秒的辐射速度变化相对应。上文显示的外行星外行星造成的多普勒移动的振幅对眼睛来说是看不见的。

Our ability to detect smaller planets is limited by the precision with which we can measure the shifts of spectral lines. Jupiter induces a radial velocity in the sun of about 12 m/s with a periodicity of about 12 years. To detect Jupiter, we would need to measure a 12-year back-and-forth shift in the spectral lines of 0.01 pixel. This requires that we control the stability of our instrument to much better than this precision and maintain the control over at least 12 years. Impressively, this is the state of the art: astronomers can measure wavelength shifts to the level of 0.001 pixel (1 m/s) with decades-long stability. However, detecting the stellar reflex velocity from a planet like the Earth is a much greater challenge. The Earth induces a velocity of about 10 cm/s in the Sun. This corresponds to a one-year back-and-forth shift of 0.0001 pixel. New are now being developed to try to find other examples of that might harbor life.

::我们探测小行星的能力受到我们测量光谱线变化的精确度的限制。木星在太阳中诱发的辐射速度约为12米/ 秒左右, 周期约为12年。要探测木星, 我们需要测量光谱线0.01像素的连续和连续12年的移动速度。这要求我们控制仪器的稳定性比这个精确度要好得多, 并保持至少12年的控制力。令人印象深刻的是, 这是艺术的状态: 天文学家可以测量波长变化到 0.001 像素(1 m/ s) 的水平, 并且有数十年的稳定性。然而, 探测像地球这样的行星的恒星反应速度是一个更大的挑战。地球在太阳中产生大约10厘米/ 的速度。这相当于 1 年的背移动 0. 001 像素。正在开发新来尝试寻找其他可能保存生命的例子。

Detecting planets from velocities
::从速度探测行星

To detect a planet with the Doppler technique, many spectra must be obtained that span the complete orbital period of the star-planet system. Of course, astronomers don't know the orbital period in advance, so in practice, they take as many spectra as possible and then use mathematical and statistical methods to search for repeating changes in the radial velocity.
::为了探测多普勒技术的行星,必须获得覆盖恒星平面系统整个轨道周期的许多光谱。当然,天文学家并不事先知道轨道周期,因此实际上,他们尽可能多地使用光谱,然后使用数学和统计方法来寻找射线速度的重复变化。

The below depicts the orbit of a star as a dashed circular path that is viewed edge-on by an observer to the right. The velocity of the star is constant in this figure, however the projected radial velocity along our line of sight is changing. At point A, the star moves toward the observer and the spectrum of the star is blue-shifted (the measured wavelengths are shorter). At point E, the star moves away from the observer and the spectrum of the star is red-shifted (the measured wavelengths are shifted to longer, redder wavelengths). At point C, there is no radial velocity - all of the motion is tangential to our line of sight. At points B and D, only the projected radial component of the velocity (velocity times the sine of the orbital inclination) can be measured in the stellar spectrum.
::以下将恒星的轨道描述为由右侧观察者观察的虚圆形路径。恒星的速度在这个数字中是恒星的不变的, 然而我们视线沿线的预测辐射速度正在变化。在A点, 恒星向观察者移动, 恒星的频谱是蓝色的( 测量的波长较短 ) 。在E点, 恒星从观察者移动, 恒星的频谱是红色的( 测量的波长被移到更长的、红波长 ) 。在C点, 没有辐射速度 - 所有运动都与我们视线相近。在B点和D点, 只有预测的速度的辐射部件( 轨道倾角的正弦速度乘以速度) 才能在星光谱中测量。

The Doppler technique is only sensitive to velocity along our line of site (radial velocity). As the star orbits the center of mass, the projected component of the radial velocity is calculated by measuring the change in the wavelength of absorption lines in the stellar spectrum. What is the radial velocity that we measure when the star is traveling tangential to our line of site (point C)?
::多普勒技术只对沿我们地点线的速度(辐射速度)敏感。当恒星绕着质量中心运行时,射线速度的预测组件是通过测量恒星频谱吸收线波长的变化来计算的。当恒星漂移到我们地点线(C点)时,我们测量的射线速度是什么?

The orbit of the planet cannot be seen; instead we model the time series radial velocity measurements of the star to infer several attributes of the orbit:
::无法看到地球轨道;相反,我们模拟恒星的时序辐射速度测量,以推断轨道的若干属性:

the velocity amplitude, $\begin{align*}K\end{align*}$
::速度振幅, K

the orbital period, $\begin{align*}P\end{align*}$
::轨道周期,P

orbital eccentricity, $\begin{align*}e\end{align*}$
::轨道偏心,e

rotation of the orbit, $\begin{align*}\omega\end{align*}$
::轨道旋转,_______________________________________________________________________________________________________________________________________

time of periastron passage, $\begin{align*}{T}_{p}\end{align*}$
::直径直径时, Tp

These parameters can then be used to calculate the semi-major axis and the mass of the planet times the orbital inclination using Newtonian physics.
::然后,这些参数可用来计算半主轴和行星质量乘以牛顿物理学的轨道倾角。

   $\begin{align*}K=\frac{8.95\left[{\rm cm/s}\right]}{\sqrt{1-{e}^{2}}}\frac{{m}_{pl}\sin i}{{m}_{\oplus}}{\left(\frac{{M}_{*}+{m}_{pl}}{{M}_{\odot}}\right)}^{-2/3}{\left(\frac{P}{year}\right)}^{-1/3}\end{align*}$       [Eqn 2]
::K=8.95[cm/s]1-e2mplsin im(MmplM)-2/3(P年)-1/3[Eqn 2]

- where $\begin{align*}K\end{align*}$ is the velocity semi-amplitude in cm/s,
::- K是以厘米/秒为单位的高速半光度,

- $\begin{align*}{m}_{pl}\sin i\end{align*}$ is the mass of the planet in units of Earth masses times the sine of the orbital inclination,
::- mplsini是地球质量单位中的地球质量乘以轨道倾角的正弦,

- $\begin{align*}{m}_{\oplus}\end{align*}$ is the mass of the Earth - so the ratio $\begin{align*}\frac{{m}_{pl}}{{m}_{\oplus}}\end{align*}$ is dimensionless,
::- m 是地球的质量 - 所以比例mplm是无维的,

- $\begin{align*}{M}_{*}\end{align*}$ is the mass of the star - the mass of the planet can be considered negligible and dropped,
::- M* 是恒星的质量 - 地球的质量可以被认为是可忽略不计和下降,

- $\begin{align*}{M}_{\odot}\end{align*}$ is the mass of the sun, so the ratio $\begin{align*}\frac{{M}_{*}}{{M}_{\odot}}\end{align*}$ is dimensionless,
::- M是太阳的质量, 所以比例MM是无维的,

- $\begin{align*}P\end{align*}$ is the orbital period in years (so this ratio is also dimensionless).
::- P是各年的轨道周期(因此这个比率也是无维的)。

Conceptual questions

::概念问题

What is the value of $\begin{align*}K\end{align*}$ if $\begin{align*}{m}_{pl}\sin{i}=1\,{m}_{\oplus}\end{align*}$ , $\begin{align*}{M}_{*}=1{M}_{\odot}\end{align*}$ , $\begin{align*}e=0\end{align*}$ and $\begin{align*}P=1\,year\end{align*}$ ?
::如果 mplsini=1m, M1M, e=0 和 P=1 year, K 值是多少 ?

Qualitatively, how does the value of $\begin{align*}K\end{align*}$ change if the orbital eccentricity is greater than zero?
::从质量上讲,如果轨道偏心大于零,K值如何改变?

Qualitatively, how does the value of change if the orbital period is less than one year?
::在质量上,如果轨道周期不到一年,变化的价值如何?

Why $\begin{align*}{m}_{pl}\sin{i}\end{align*}$ ?
::为什么 mplsini?

Equation 2 relates the radial velocity amplitude of the star to $\begin{align*}{m}_{pl}\sin i\end{align*}$ , rather than to the actual mass of the planet. What does that mean? The Doppler technique measures the projected 1-dimensional velocities of stars. When an orbit is viewed edge-on ( $\begin{align*}\sin{i}={90}^{\circ}\end{align*}$ ) we see the full amplitude of this sinusoidally varying projection. If an orbit is face-on ( $\begin{align*}\sin{i}={0}^{\circ}\end{align*}$ ), there is no radial component to the stellar velocity; the orbit is undetectable with this technique. For orbits that are inclined in between these values, the velocity semi-amplitude, $\begin{align*}K\end{align*}$ , decreases with the sine of the inclination. We cannot distinguish whether $\begin{align*}K\end{align*}$ is smaller because the orbiting mass or the inclination is smaller; we only model the product $\begin{align*}{m}_{pl}\sin{i}\end{align*}$ . The true mass is given by:
::方程式 2 将恒星的弧速度振幅与 mlsini 相连接, 而不是与行星的实际质量。这意味着什么 ? 多普勒技术测量了恒星的预测一维速度。当一个轨道在边缘( sini=90) 时, 我们可以看到这个正弦不同投影的全振幅。如果一个轨道在面( sini=0) 上, 星体速度没有辐射元件; 轨道与这个技术是无法探测的。对于这些数值之间倾角的轨道, 速度半光度, K, 以正弦的角递减。我们无法区分 K 是否较小, 因为轨道质量或倾角较小; 我们只能模拟产品 mplsini 。真正的质量由以下提供:

   $\begin{align*}{m}_{pl}=\frac{{m}_{pl}\sin{i}}{\sin{i}}\end{align*}$ .       [Eqn 3]
::mpl=mplsinisini。 [项目3]

While we cannot solve for inclination, equation 3 shows that because $\begin{align*}\sin{i}\end{align*}$ ranges between 0 and 1, $\begin{align*}{m}_{pl}\sin{i}\end{align*}$ is a lower limit to the true mass of the planet.
::虽然我们无法解决倾角问题,但方程3表明,由于sini的范围介于0至1之间,mplsini是地球真正质量的下限。

Statistical probability for $\begin{align*}\sin{i}\end{align*}$

::统计概率

For randomly oriented inclinations, the probability of drawing a particular $\begin{align*}\sin{i}\end{align*}$ is not uniform. Instead, the probability of observing an orbit with an inclination $\begin{align*}\Delta i\end{align*}$ between $\begin{align*}{i}_{1}\end{align*}$ and $\begin{align*}{i}_{2}\end{align*}$ scales as the difference between the cosine of those angles:

::对于随机方向的倾角,绘制特定的 sini 的概率并不统一。相反, 以 i1 和 i2 比例尺之间的倾角 i 观察轨道的概率, 作为这些角的余弦的差数 :

                                         $\begin{align*}\mathcal{P}=\left| \cos{{i}_{1}}-\cos{{i}_{2}}\right|\end{align*}$          [Eqn 4]
::[第4条]

So, there is an 86% probability that the inclination of a random orbit is between $\begin{align*}{90}^{\circ}\end{align*}$ and $\begin{align*}{30}^{\circ}\end{align*}$ . For these typical orbits, the true mass of the planet would be within a factor of two of the measured $\begin{align*}{m}_{pl}\sin{i}\end{align*}$ . Conversely, there is only a 14% probability that an orbital inclination is between $\begin{align*}{30}^{\circ}\end{align*}$ and $\begin{align*}{0}^{\circ}\end{align*}$ (yielding a true mass more than twice $\begin{align*}{m}_{pl}\sin{i}\end{align*}$ ).
::随机轨道的倾角在 90 至 30 之间的概率为 86%。对于这些典型的轨道来说, 地球的真正质量将介于测量的 mplsini 的二倍之内。相反, 轨道倾角在 30 至 0 之间的概率只有 14%( 实际质量超过 0. 2 mplsini ) 。

Real-world examples
::现实世界实例

In 1995, Michel Mayor and Didier Queloz discovered the first exoplanet around a main sequence star using the Doppler technique. The planet that they discovered has a mass similar to Jupiter's and orbits the star 51 Pegasi once every 4.23 days. The data from their 1995 discovery paper are shown in the below. Because the signal repeats, the velocities can be folded so that the orbital periods repeat. This "phase-folded" data is a helpful way to display relatively short periodic signals and clearly demonstrates that the signal is repeating in a predictable way.
::1995年,Michel Mayor和Didier Queloz利用多普勒技术在主要序列恒星周围发现了第一个外行星。他们发现的行星质量类似于木星,每4.23天运行51号恒星Pegasi,1995年发现纸上的数据显示在下面。由于信号重复,速度可以折叠,以便轨道周期重复。这种“相叠式”数据是一种有用的方法,可以显示较短的周期信号,并清楚地显示信号正在以可预测的方式重复。

In the data from the Mayor & Queloz 1995 paper, you can see that from September to November in 1994, the radial velocities for 51 Pegasi were changing. This perplexed Didier Queloz, who was a graduate student working with Professor Mayor. To better understand the velocity variations, he began taking more data. Mayor and Queloz developed a mathematical model (shown as the solid line) that fits the velocity changes of the star and also describes Keplerian orbital motion. It is quite an empowering feeling to develop a model like this and to then watch the future velocities of the star follow your predictions.
::在市长 & Queloz 1995 论文的数据中,你可以看到,1994年9月至11月,51个Pegasi的辐射速度在变化。这个与市长教授合作的研究生Didier Queloz为难的Didier Queloz开始掌握更多的数据。市长和Queloz开发了一个符合恒星速度变化的数学模型(称为固态线 ) , 并描述了Keplerian轨道运动。开发这样一个模型,然后观察未来的恒星速度跟随你的预测,是一种相当增强能力的感觉。

Radial velocity of the star 51 Peg over four epochs after removing the constant velocity of the star. he radial velocity data in the images above were taken at different times between 1994 and 1995, but are plotted against an angle; what does that mean?
::恒星51Peg在去除恒星恒星恒定速度后,在四度上的辐射速度。上面图像中的辐射速度数据是在1994年至1995年的不同时间拍摄的,但是在一个角度上绘制的; 这意味着什么?

Queloz and Mayor could not quite believe what they were seeing. A Jupiter-mass planet in a 4-day orbit was very different from any of the planets in our solar system. In their paper, they discuss the alternative interpretations such as stellar pulsations and effectively rule them out. They conclude that the most likely interpretation is an orbiting planetary mass companion.
::基洛兹和市长无法完全相信他们所看到的。四天轨道上的木星行星与太阳系中的任何行星都有很大不同。在他们的论文中,他们讨论了恒星脉冲等替代解释,并有效地排除了这些解释。他们的结论是,最有可能的解释是环绕行星质量伴星。

Because they derive $\begin{align*}{m}_{planet}\sin{i}\end{align*}$ , they note that the true mass may be larger than one Jupiter mass. Some skeptics believed that Mayor and Queloz had simply detected a stellar binary system that was oriented nearly face-on. However, an inclination of less than $\begin{align*}{1}^{\circ}\end{align*}$ is required to pump $\begin{align*}{m}_{pl}\sin{i}\end{align*}$ up to the stellar mass regime of 70 Jupiter masses. According to equation 4, there is only 1 chance in 10,000 that they would have observed such a low inclination orbit.
::因为他们获得 mplanetsini, 他们注意到真正的质量可能大于一个木星质量。一些怀疑论者认为市长和奎罗兹只是发现了一个近乎表面的恒星二进制系统。但是, 将 mplsini 泵到70个木星质量的恒星系统时, 需要的倾斜度小于 1 。根据方程式 4, 一万分之一的概率是他们能够观察到这样一个低倾角轨道。

The next few exoplanets
::接下来的少数外行星

Mayor and Queloz's discovery of an exoplanet in such a short orbital period was a game-changer. A team of astronomers at San Francisco State University, Marcy and Butler, were also trying to find exoplanets using the Doppler technique. They had a backlog of data because they were collecting about 50 spectra per night, but it took 24 hours to analyze a single spectrum on the slower computers of the day. Spurred on by the discovery of 51 Peg b, Sun Microsystems made a donation to the SFSU team and they quickly crunched through their observations, discovering Jupiter-like planets around 70 Virginis and 47 Ursa Majoris in their sample of 120 stars. The second of these, 47 UMa b, was very much like 51 Peg b - a Jupiter-mass planet in an orbit of just a few days.
::位于旧金山州立大学、玛西和巴特勒(Marcy and Butler)的一组天文学家也在试图利用多普勒技术寻找外行星。他们的数据积压,因为他们每晚收集大约50个光谱,但用24小时分析日间速度较慢的计算机的单一光谱。在发现51个比格(Peg b)之后,太阳微系统向SFSU团队捐赠了一笔捐款,他们通过观察迅速收缩,在120颗恒星的样本中发现了约70个像木星的行星和47个像木星的行星。第二颗行星,47个UMA b,非常接近51个比格(B)-木星行星在短短几天的轨道上。

However, the data for 70 Vir b (shown below) told a different story.
::然而,70 Vir b(如下表所示)的数据却有不同的情况。

Phase-folded radial velocities for the star 70 Virginis reveals a planet with a mass of 6.6 times the mass of Jupiter in a 116 day orbit. Why does the shape of the radial velocity curve look different from the sinusoidal variation seen for 51 Peg b?
::星70维尔吉尼斯星的分层辐射速度显示,在116天轨道上,行星质量是木星质量的6.6倍。为什么射线速度曲线的形状看起来不同于51 Peg b 所见的正弦变异?

Instead of the sinusoidal velocity variation seen with 51 Peg b, this planet has a more peaked velocity variation revealing an orbit with eccentricity of 0.4. The planet mass (6.6 times the mass of Jupiter) is also much larger, producing greater velocity variations in 70 Virginis. To the skeptics, the discovery of yet another massive planet was further support for the idea that nearly face-on binary star systems were being discovered rather than exoplanets. The fact that this object was in an eccentric orbit added to the doubts - planets in our solar system are in nearly circular orbits. Surely the rest of the cosmos would be like us?

::与51 Peg b 所观察到的正弦形速度变异相反,这个星球的高度速度变异更高峰,揭示轨道的偏心度为0.4。行星质量(6.6倍于木星质量)也大得多,在70个维吉尼亚州产生更大的速度变异。对于怀疑论者来说,发现另一个巨大的行星进一步支持了近表面的二元星系统被发现而不是外行星的想法。这个物体在偏心轨道上的事实增加了疑问——太阳系中的行星几乎在环绕轨道上。宇宙的其余部分肯定会像我们一样吗?

Practice with the radial velocity simulator
::使用无线电速度模拟器的做法

There are a lot of concepts to understand with the Doppler technique. First, we use the spectrum of the star to measure wavelength shifts that correspond to changes in the velocity of the star. Second, we see only the projected radial component of the stellar velocity (this leads to a sinusoidal variation in the signal). Third, we don't know the inclination of the orbit - this tilt of the orbit means that the sinusoidal signal will be largest when viewed edge-on ( $\begin{align*}{90}^{\circ}\end{align*}$ inclination) and smaller as the inclination tilts toward face-on. This means that we only measure $\begin{align*}{m}_{planet}\sin{i}\end{align*}$ with the Doppler method.

::多普勒技术有许多概念需要理解。首先, 我们使用恒星的频谱来测量波长变化, 与恒星速度的变化相对应。其次, 我们只看到恒星速度的预测半径部件( 这导致信号的正弦变异 ) 。第三, 我们不知道轨道的倾斜度 - 轨道的倾斜度意味着当看到边缘( 90 倾角) 时, 正弦信号将最大, 与面向面的倾斜一样小。这意味着我们只用多普勒方法测量 mplanetsin i 。

Let's walk through a series of exercises with the Nebraska Astronomy Applet Project (NAAP) to help develop your intuition and understanding of the Doppler method. You will need to download the Simulations package (will install in your Applications directory, open Extrasolar Planets, Exoplanet Radial Velocity Simulator) .
::让我们与内布拉斯加天文小程序项目(NAAP)进行一系列练习, 以帮助发展您的直觉和对多普勒方法的理解。您需要下载模拟软件包( 将安装在您的应用程序目录中 , 打开太阳外行星, Exoplanet 辐射速度模拟器 ) 。

Begin by opening the simulator and setting up the inputs to match the values shown in the below. Simulated radial velocities are ``phase-folded'' in the upper right hand plot. The radial velocities are obtained as a function of time, but if you repeat observations over more than one orbital period, the data can be folded so that all of the peaks and troughs of the curve line up. This is routinely done by astronomers to build evidence for repeating signals.

::从打开模拟器开始, 并设置与下面显示的值匹配的输入。模拟的辐射速度在右上方的手绘图中是“ 相相叠的 ” 。辐射速度是按时间函数获得的, 但如果您在不止一个轨道期间重复观测, 数据可以折叠, 以便曲线线上的所有峰值和槽。由天文学家例行这样做, 以建立重复信号的证据。

Initial setup: show multiple windows, Inclination 76.8 degrees, longitude 45 degrees, 1 Msun star, planet mass 1 Mjup, semi-major axis 5.2 AU, eccentricity 0, show theoretical curve, show simulated measurements, noise = 2.0 m/s, number of observations = 30. The semi-amplitude of the radial velocities should be about 12 m/s (read this off the y-axis of the RV plot).
::初始设置: 显示多个窗口、倾角76.8度、纬度45度、 1 兆星、行星质量 1 Mjup、半主轴 5.2 AU、偏心度 0、显示理论曲线、显示模拟测量、噪音= 2.0 m/s、观测次数= 30 。半准光度辐射速度应约为 12 m/s( 从 RV 绘图的 y 轴上读取)。

Simulation Exercises
::模拟演习

First, make sure that you understand what the orbit visualizations are showing in the upper left corner of the control panel. There are four different views:

side view - looking edge-on at the orbit
::左侧视图 - 向轨道边边边看

earth view - the orbit is now tilted by the 76.8 degrees that you specified.
::地球视图 - 轨道现在被您指定的76.8度倾斜。

orbit view - this is looking at the orbit face-on
::轨道视图 - 正在查看轨道的相对面

3-d view with arrows indicating viewing angles for 1 and 2 above.
::3-d 视图,以箭头显示上面1和2的视图角度。

::首先,请确保您了解控制面板左上角显示的轨道可视化。有四种不同的观点:侧视图-在轨道地球视图上边观-轨道现在被您指定的76.8度倾斜。轨道视图- 正在查看轨道对面的三维视图, 上面的箭头显示以上 1 和 2 的视图角度。

Now, rotate the inclination bar and notice two things: the tilt of the orbit changes in the earth view panel and the amplitude of the RV signal decreases as the inclination goes toward zero and increases as the inclination goes to $\begin{align*}{90}^{\circ}\end{align*}$ .
::现在,旋转倾角栏并注意两件事:地球观察面板轨道变化的倾斜和RV信号的振幅随着倾角向零和倾角向90而增加而下降。

Reset the inclination to $\begin{align*}{76.8}^{\circ}\end{align*}$ . Now increase the number of observations from 30 to 300 to see how confidence increases with more data.
::将倾角重置为76.8。现在将观测次数从30次增加到300次, 以了解更多的数据如何增加信任度。

Toggle the "theoretical curve" off and slide the "noise" bar (representing the measurement precision) from 1 m/s to 12 m/s. When the measurement uncertainty (noise) is comparable to the signal (12 m/s), it is only possible to have a convincing detection if there are many observations. As you dial down the number of observations from 300 back to 30, the underlying signal is less certain.
::切除“ 理论曲线” , 将“ 噪音” 栏( 代表测量精度) 从 1 m/ s 向 12 m/ s 滑动。当测量不确定性( 噪音) 与信号( 12 m/ s ) 相仿时, 只有当观测次数众多时, 才有可能有令人信服的检测。当您将观测次数从 300 下调到 30 时, 底线的信号就不那么确定。

Check to see how the mass of the star affects the amplitude of the RV signal (notice that the numbers on the y-axis will change). A lower mass star is easier for a planet to push around than a high mass star.
::检查一下恒星的质量如何影响 RV 信号的振幅( 注意 Y 轴上的数字将会改变 ) 。低质量恒星比高质量恒星更容易被行星推动。

The Earth has a mass that is 0.0032 times the mass of Jupiter. Change the mass in the simulator to this value. Is there any way of convincingly detecting an Earth analog (Earth-mass planet at 1 AU) around a solar mass star with the precision of the simulator? Are there any orbits where you could convincingly detect an Earth-mass planet (i.e., any mass star, any semi-major axis)?
::地球质量是木星质量的0.0032倍。将模拟器的质量改变为这个值。是否有办法能令人信服地以模拟器的精确度探测太阳质量恒星周围的地球模拟行星( 位于1AU1的地球质量行星 ) ? 是否有任何轨道可以令人信服地探测地球质量行星( 即任何质量恒星, 任何半主轴) ?

版权所有 © 2024 由瓜瓜科技thewaytolearn.cn设计。保留所有权利。