1.2 点和切合产品

Section outline

• Select section General

  Collapse Expand

  General

  Collapse all Expand all

  • Select activity 新闻通告

    

    新闻通告 Forum
• Select section 点和交点产品

  Collapse Expand

  点和交点产品

  播放段落

  Dot Product
  ::点产品

  播放段落

  The dot product of two vectors is essentially a function that takes in two vectors and outputs a scalar. There are two definitions of a dot product, an algebraic definition and a geometric definition.  
  ::两个矢量的圆点产物基本上是一种函数,在两个矢量中产生一个星标。对圆点产物有两个定义,一个代数定义和一个几何定义。

   

  播放段落

  Algebraically speaking the dot product of two vectors  $\begin{array}{r}\stackrel{\to }{v}\text{ and }\stackrel{\to }{w}\end{array}$  denoted as  $\begin{array}{r}\stackrel{\to }{v}\cdot \stackrel{\to }{w}\end{array}$  is the sum of the product of the respective entries, so if  $\begin{array}{r}\stackrel{\to }{v}=\left[\begin{array}{c}{v}_1\\ v_2\end{array}\right]\text{ and }\stackrel{\to }{w}=\left[\begin{array}{c}{w}_1\\ w_2\end{array}\right]\end{array}$  you'll get $\begin{array}{r}\stackrel{\to }{v}\cdot \stackrel{\to }{w}=v_1\cdot w_1+v_2\cdot w_2\end{array}$ .
  ::代数说两个矢量的圆点产物 v 和 w 被标记为 vw 是各个条目的产物的总和, 所以如果 v v1v2 和 w[w1w2], 你会得到vwv1w1+v2w2 。

   

  播放段落

  Generally speaking if  $\begin{array}{r}\stackrel{\to }{v}\text{ and }\stackrel{\to }{w}\end{array}$  exist in n-dimensions 
  ::一般说来,如果 v 和 w 存在于 n- dimension 中

  播放段落

  where  $\begin{array}{r}\stackrel{\to }{v}=\left[\begin{array}{c}{v}_1\\ v_2\\ \cdot \\ \cdot \\ \cdot \\ v_{n-1}\\ v_n\end{array}\right]\text{ and }\stackrel{\to }{w}=\left[\begin{array}{c}{w}_1\\ w_2\\ \cdot \\ \cdot \\ \cdot \\ w_{n-1}\\ w_n\end{array}\right]\end{array}$  the dot product of these two vectors is
  :v1v2vn-1vn) 和 w[w1w2wn-1wn] 这两个矢量的点产物是

  播放段落

   

  $$\begin{array}{r}\stackrel{\to }{v}\cdot \stackrel{\to }{w}=\underset{i=1}{\overset{n}{\sum }}{v}_i{w}_i\end{array}$$

   
  ::{\fn华文楷体\fs16\1cHE0E0E0}维维维

  播放段落

  If you think about matrix multiplication, which we'll go more in depth in later, we see  $\begin{array}{r}\stackrel{\to }{v}\cdot \stackrel{\to }{w}={\stackrel{\to }{v}}^T\stackrel{\to }{w}\end{array}$  or the product of the matrices  $\begin{array}{r}{\stackrel{\to }{v}}^T\text{ and }\stackrel{\to }{w}\end{array}$   because vectors are essentially matrices with only 1 column.
  ::如果您想一下矩阵乘法, 稍后我们会更深入地进行, 我们可以看到 vwvvTw 或矩阵 vT 和 w的产物, 因为矢量基本上是只有一列的矩阵。

  播放段落

  Now before I introduce the geometric definition let's first  compute a couple examples.
  ::在我介绍几何定义之前 先计算几个例子

  播放段落

  $\begin{array}{r}\stackrel{\to }{v}=\left[\begin{array}{c}1\\ 1\end{array}\right]\end{array}$  and  $\begin{array}{r}\stackrel{\to }{w}=\left[\begin{array}{c}2\\ 3\end{array}\right]\end{array}$
  ::v[11] 和 w[23]

  播放段落

  Now  $\begin{array}{r}\stackrel{\to }{v}\cdot \stackrel{\to }{w}=1\cdot 2+1\cdot 3=2+3=5\end{array}$ .
  ::现在 vw12+13=2+3=5。

   

  播放段落

  Let's try another example,  $\begin{array}{r}\stackrel{\to }{u}=\left[\begin{array}{c}-1\\ 3\\ -5\end{array}\right]\text{ and }\stackrel{\to }{x}=\left[\begin{array}{c}7\\ 3\\ -4\end{array}\right]\end{array}$   then    $\begin{array}{r}\stackrel{\to }{u}\cdot \stackrel{\to }{x}=-1\cdot (7)+3\cdot (3)+(-4)\cdot (-5)=-7+9+20=22\end{array}$ .
  ::让我们再举另一个例子,u[-13-5]和x[73-4],然后ux1(7)+3(3)+(-4)(-5)7+9+20=22。

  ---

   

   

  播放段落

  Now let  $\begin{array}{r}\stackrel{\to }{u}=\left[\begin{array}{c}1\\ 2\\ -3\\ 12\end{array}\right]\text{ and }\stackrel{\to }{v}=\left[\begin{array}{c}-1\\ 2\\ 7\end{array}\right]\end{array}$ .
  ::现在让u[12-312]和v[-127]。

  播放段落

  Now this may seem a bit unfamiliar as the dimension of these two vectors are different. However, a vector in 3 dimensions exists in 4 dimensions it just has a 0 in the 4th entry. Another way to see this is how a point on the x-axis is a one-dimensional object, but exists in n-dimensional space.
  ::这似乎有点陌生, 因为这两个矢量的维度不同。 但是, 3维的矢量存在于4维中, 它只在第4项中有一个0。 另一种观察方式是 X 轴上的一个点如何是一维的物体, 但存在于 n- 维空间中 。

  播放段落

  Hence our dot product can be written as
  ::因此,我们的点产品可以写成

  播放段落

   

  $$\begin{array}{r}\stackrel{\to }{u}\cdot \stackrel{\to }{v}=1(-1)+2(2)+7(-3)+0(12)=2.\end{array}$$

  
  ::uv1(-1)+2(2)+7(-3)+0(12)=2。

   

  ---

   

  播放段落

  Now that we have gone over what the dot product means algebraically let's talk about the geometric definition.
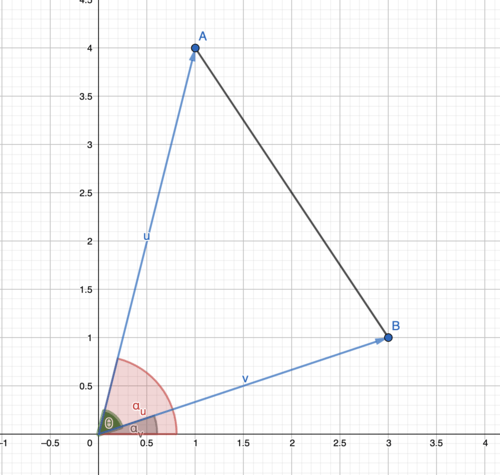
  ::现在我们已经翻过点产品的意思了 让我们来谈谈几何定义吧

  播放段落

  Given  $\begin{array}{r}\stackrel{\to }{a},\stackrel{\to }{b},\stackrel{\to }{a}\cdot \stackrel{\to }{b}=||\stackrel{\to }{a}||\cdot ||\stackrel{\to }{b}||\text{cos}(\theta )\end{array}$  where  $\begin{array}{r}\theta \end{array}$  is the angle in between the two vectors. This may seem a little far fetched, but first consider the following diagram for a proof
  ::在 a , b , a

  

  播放段落

  You have two vectors  $\begin{array}{r}\stackrel{\to }{u}\text{ and }\stackrel{\to }{v}\end{array}$  where $\begin{array}{r}{\alpha }_v\text{ and }{\alpha }_u\end{array}$  are the angles between the vectors  $\begin{array}{r}\stackrel{\to }{v}\text{ and }\stackrel{\to }{u}\end{array}$  and the x-axis, respectively. And  $\begin{array}{r}\theta \text{ as defined earlier is }{\alpha }_u-{\alpha }_v\end{array}$ .
  ::您有两个矢量 u 和 v 和 v , 其中αv 和 αu 分别是矢量 v 和 u 和 u 与 x 轴之间的角。 前面定义的 是 αu v 。

   

  播放段落

  Now  we recall that  $\begin{array}{r}\stackrel{\to }{v}=\left[\begin{array}{c}||\stackrel{\to }{v}||\text{cos}({\alpha }_v)\\ ||\stackrel{\to }{v}||\text{sin}({\alpha }_v)\end{array}\right]\end{array}$  and likewise  $\begin{array}{r}\stackrel{\to }{u}=\left[\begin{array}{c}||\stackrel{\to }{u}||\text{cos}({\alpha }_u)\\ ||\stackrel{\to }{u}||\text{sin}({\alpha }_u)\end{array}\right].\end{array}$  
  ::现在,我们记得,vvcos(αv)vvsin(αv)]和uucos(αu)usin(αu)]。

  播放段落

  Hence $\begin{array}{r}\stackrel{\to }{u}\cdot \stackrel{\to }{v}=||\stackrel{\to }{v}||\cdot ||\stackrel{\to }{u}||\text{cos}({\alpha }_v)\text{cos}({\alpha }_u)+||\stackrel{\to }{v}||\cdot ||\stackrel{\to }{u}||\text{sin}({\alpha }_v)\text{sin}({\alpha }_u)\end{array}$ .
  ::Sonuvvucos(α)cos(α)vusin(α)sin(α)sin(α)sin(α)。

  播放段落

  After factoring out the products of the magnitudes of the vectors you get the formula for the cosine of the difference of the angles  $\begin{array}{r}{\alpha }_u\text{ and }{\alpha }_v\end{array}$  which is by definition  $\begin{array}{r}\theta \end{array}$  and yields the final result  $\begin{array}{r}\stackrel{\to }{u}\cdot \stackrel{\to }{v}=||\stackrel{\to }{u}||\cdot ||\stackrel{\to }{v}||\text{cos}(\theta )\end{array}$ . Now this proves the formula in two dimensions. The proof here is a bit more geometrically intuitive, but for sake of completeness I shall prove this formula for n-dimensions.
  ::将矢量大小的产物计算出来后,您可以得到αu 和αv 角的余弦值的公式,根据定义,该公式是 ,并产生最终结果 uvuvççcos() 。 现在,这从两个维度证明了公式。 这里的证明是更几何直观的, 但为了完整起见, 我将证明这个公式为 n- dimension 。

  ---

  播放段落

  First we need a couple of lemmas to prove the main theorem. So let's show that the geometric definition  is the same as the algebraic definition by assuming the geometric definition and showing it is equal to the algebraic definition. Going either way works, but it is easier to get the first way.  
  ::首先,我们需要用几颗 Lemmas 来证明主要理论。 因此让我们来证明几何定义与代数定义相同, 假设几何定义, 并显示它等于代数定义。 无论哪种方法都行得通, 但选第一种方法比较容易。

  播放段落

  We now need to show a couple of lemmas in order to prove this.
  ::我们现在需要展示一对夫妇的麻麻 以证明这一点。

   

  播放段落

  Lemma 1:   $\begin{array}{r}\stackrel{\to }{x}\cdot \stackrel{\to }{x}=||\stackrel{\to }{x}|{|}^2\end{array}$
  ::Lemma 1: xxx2

  播放段落

  Proof:   By definition  $\begin{array}{r}\stackrel{\to }{x}\cdot \stackrel{\to }{x}=||\stackrel{\to }{x}||\cdot ||\stackrel{\to }{x}||\cdot \text{cos}(\theta )\end{array}$  and  $\begin{array}{r}\theta \end{array}$  is defined to be the angle between these two vectors and because these two vectors are the same  $\begin{array}{r}\theta =0\end{array}$  so  $\begin{array}{r}\text{cos}(\theta )=1\end{array}$  and  $\begin{array}{r}\stackrel{\to }{x}\cdot \stackrel{\to }{x}=||\stackrel{\to }{x}||\cdot ||\stackrel{\to }{x}||=||\stackrel{\to }{x}|{|}^2\end{array}$ .
  ::证明:根据定义, xxxxxxxxxcos() 和 被定义为这两个矢量之间的角,并且因为这两个矢量是相同的0 so cos()=1 和 xxxxxxxx2。

  播放段落

  Lemma 2: $\begin{array}{r}\stackrel{\to }{x}\cdot (\stackrel{\to }{y}+\stackrel{\to }{z})=\stackrel{\to }{x}\cdot \stackrel{\to }{y}+\stackrel{\to }{x}\cdot \stackrel{\to }{z}\end{array}$
  ::Lemma 2: x(yz) =xyxz

  播放段落

  Lemma 3:   $\begin{array}{r}\stackrel{\to }{x}\cdot \stackrel{\to }{y}=\stackrel{\to }{y}\cdot \stackrel{\to }{x}\end{array}$
  ::Lemma 3: xyyx

  播放段落

  Lemmas 2 and 3 are left as exercises for the reader to prove.
  ::Lemmas 2和3留作练习,供读者证明。

  ---

   

  播放段落

  Now to prove the main theorem:
  ::现在来证明主要理论:

  播放段落

  Proof: Looking at Lemma 1  $\begin{array}{r}\stackrel{\to }{x}\cdot \stackrel{\to }{x}=||\stackrel{\to }{x}|{|}^2\end{array}$  so from here deduce that  $\begin{array}{r}(\stackrel{\to }{x}+\stackrel{\to }{y})\cdot (\stackrel{\to }{x}+\stackrel{\to }{y})=||\stackrel{\to }{x}+\stackrel{\to }{y}|{|}^2.\end{array}$  Now using basic algebra  $\begin{array}{r}(\stackrel{\to }{x}+\stackrel{\to }{y})\cdot (\stackrel{\to }{x}+\stackrel{\to }{y})=\stackrel{\to }{x}\cdot (\stackrel{\to }{x}+\stackrel{\to }{y})+\stackrel{\to }{y}\cdot (\stackrel{\to }{x}+\stackrel{\to }{y})\end{array}$
  ::校对: 从这里查看 Lemma 1 xxxx2, 从这里可以推断 (xy) (xy) xy2. 现在使用基本代数 (xy) (xy) =x(xy) +y(xy)

  播放段落

  Now by lemma 2 you get  $\begin{array}{r}(\stackrel{\to }{x}+\stackrel{\to }{y})\cdot (\stackrel{\to }{x}+\stackrel{\to }{y})=\stackrel{\to }{x}\cdot \stackrel{\to }{x}+\stackrel{\to }{x}\cdot \stackrel{\to }{y}+\stackrel{\to }{y}\cdot \stackrel{\to }{x}+\stackrel{\to }{y}\cdot \stackrel{\to }{y}\end{array}$  now we can simplify this using lemmas 1 and 3 to get  $\begin{array}{r}||\stackrel{\to }{x}|{|}^2+||\stackrel{\to }{y}|{|}^2+2\stackrel{\to }{x}\cdot \stackrel{\to }{y}\end{array}$ . Now we have the equality  $\begin{array}{r}(\stackrel{\to }{x}+\stackrel{\to }{y})\cdot (\stackrel{\to }{x}+\stackrel{\to }{y})=||\stackrel{\to }{x}|{|}^2+||\stackrel{\to }{y}|{|}^2+2\stackrel{\to }{x}\cdot \stackrel{\to }{y}.\end{array}$  Then you can get the left hand side as  $\begin{array}{r}||\stackrel{\to }{x}+\stackrel{\to }{y}|{|}^2\end{array}$  and that yields the equation  $\begin{array}{r}||\stackrel{\to }{x}+\stackrel{\to }{y}|{|}^2=||\stackrel{\to }{x}|{|}^2+||\stackrel{\to }{y}|{|}^2+2\stackrel{\to }{x}\cdot \stackrel{\to }{y}\end{array}$ . 
  ::现在通过 lemma 2 , 您可以得到 (xy) (xy) =xxxxxyy x xy y 现在我们可以用 lemmas 1 和 3 简化它, 来获得 x2y2+2xy。 现在我们有平等 (xy) (xy) (xy) x2 2+2xy 。 然后您可以将左手侧作为xy2 并产生等式 。

  播放段落

  Next write these magnitudes squared as summations to get  $\begin{array}{r}||\stackrel{\to }{x}+\stackrel{\to }{y}|{|}^2=\underset{i=1}{\overset{n}{\sum }}(x_i+y_i{)}^2\end{array}$  and  $\begin{array}{r}||\stackrel{\to }{x}|{|}^2=\underset{i=1}{\overset{n}{\sum }}{x}_i^2\text{ whereas }||\stackrel{\to }{y}|{|}^2=\underset{i=1}{\overset{n}{\sum }}{y}_i^2\end{array}$  so  $\begin{array}{r}\underset{i=1}{\overset{n}{\sum }}(x_i+y_i{)}^2=\underset{i=1}{\overset{n}{\sum }}{x}_i^2+\underset{i=1}{\overset{n}{\sum }}{y}_i^2+2\stackrel{\to }{x}\cdot \stackrel{\to }{y}.\end{array}$  Now expanding out the left hand side  $\begin{array}{r}\underset{i=1}{\overset{n}{\sum }}(x_i+y_i{)}^2=\underset{i=1}{\overset{n}{\sum }}{x}_i^2+\underset{i=1}{\overset{n}{\sum }}{y}_i^2+\underset{i=1}{\overset{n}{\sum }}2x_i{y}_i=\underset{i=1}{\overset{n}{\sum }}{x}_i^2+\underset{i=1}{\overset{n}{\sum }}{y}_i^2+2\stackrel{\to }{x}\cdot \stackrel{\to }{y}.\end{array}$  Then subtracting the two summations of    $\begin{array}{r}\underset{i=1}{\overset{n}{\sum }}{x}_i^2\text{ and }\underset{i=1}{\overset{n}{\sum }}{y}_i^2\end{array}$  from both sides we see  $\begin{array}{r}\underset{i=1}{\overset{n}{\sum }}2x_i{y}_i=2\underset{i=1}{\overset{n}{\sum }}{x}_i{y}_i=2\stackrel{\to }{x}\cdot \stackrel{\to }{y}\end{array}$  thus  $\begin{array}{r}\stackrel{\to }{x}\cdot \stackrel{\to }{y}=\underset{i=1}{\overset{n}{\sum }}{x}_i{y}_i\end{array}$  proving the formula we set out to prove, so now we know that the algebraic and geometric definitions of the dot product are the same.
  ::下一步写入这些等量的正方形, 以获取 {xy2}2 i=1n( xi+yi) 2 和 {x2i=1nxi2 =1nyi2 所以i=1n( xi) 2i=1nxyi2+2x}。 现在将左手侧的 i=1n( xi+yi) 2i=1nxi2i=1nyi2 i=1nxi2i=1nxi2=1nxy2, 而 y2=1nnyi=1nnyi2 所以从两侧都减去 i=1n( si) 2i=1nnyi=2。 左手侧的宽度= 1nxyi=1nxxi=2} 。 因此, =1nxii=1nxi=1nxyi=1 证明 我们设定的公式是相同的, 因此我们知道 doat 产品的藻定义是相同的。

  ---

  播放段落

  Cross Product
  ::交叉产品

  播放段落

  Now that we've graduated from the dot product let's move on to the cross product. First I'll show you how to compute the cross product and then what it actually means geometrically.
  ::现在,我们已经从点产品毕业了, 让我们继续到交叉产品。 首先,我教你如何计算交叉产品, 然后它实际上意味着几何。

  播放段落

  Algebraically speaking, there are two ways to look at it. The cross product is a binary operation on two 3 dimensional vectors where  $\begin{array}{r}\stackrel{\to }{x}=\left[\begin{array}{c}{x}_1\\ x_2\\ x_3\end{array}\right]\text{ and }\stackrel{\to }{y}=\left[\begin{array}{c}{y}_1\\ y_2\\ y_3\end{array}\right]\end{array}$  and the cross product, denoted by  $\begin{array}{r}\stackrel{\to }{x}\times \stackrel{\to }{y}=\left[\begin{array}{c}{x}_2{y}_3-x_3{y}_2\\ x_3{y}_1-x_1{y}_3\\ x_1{y}_2-x_2{y}_1\end{array}\right]\end{array}$ . Another way to look at this would be to take the compute  $\begin{array}{r}\text{det}\left[\begin{array}{ccc}\hat{i}& \hat{j}& \hat{k}\\ x_1& x_2& x_3\\ y_1& y_2& y_3\end{array}\right]\end{array}$  =  $\begin{array}{r}\hat{i}\cdot \text{det}\left[\begin{array}{cc}{x}_2& x_3\\ y_2& y_3\end{array}\right]-\hat{j}\cdot \text{det}\left[\begin{array}{cc}{x}_1& x_3\\ y_1& y_3\end{array}\right]+\hat{k}\cdot \text{det}\left[\begin{array}{cc}{x}_1& x_2\\ y_1& y_2\end{array}\right]\end{array}$ . Here you are putting the basis vectors  of 3 dimensional space denoted by  $\begin{array}{r}\hat{i}=\left[\begin{array}{c}1\\ 0\\ 0\end{array}\right],\hat{j}=\left[\begin{array}{c}0\\ 1\\ 0\end{array}\right],\text{ and }\hat{k}=\left[\begin{array}{c}0\\ 0\\ 1\end{array}\right]\end{array}$  and you are scaling them by these determinants of the 2 x 2 matrices constructed by the entries of the matrix that are neither in the same row nor the same column of the matrix.  We will study basis vectors and determinants more deeply in later chapters, but for now just use your knowledge from algebra 2 or geometry. 
  ::代数论, 有两种方法可以查看它。 交叉产品是两个三维矢量的二进制操作, 其中 x[x1x2x2x3] 和 y[y1y2y3] , 以及由 xy[x2y3-x3y2x3x3y1- x3x3- x3- x2y2- x2y2- x2y2y3 = idet [x2x3x3x2x2xy2y3] 和 y[y2y3] 和 交叉产值, 由 x{x2y2x2y2] 表示。 在这里, 您正在使用 {[100], j[010] 和 k[001] 等三维空间的基础矢量。 您正在根据由矩阵条目所构建的 2 x2 矩阵中的这些决定因素进行测量, 这些决定因素既不在同一行, 也不在同一列内, 也不在矩阵的列内, , 我们将在后面研究2 。

  播放段落

  Now before I tell you what this means geometrically let's first look at a couple diagrams of calculations.
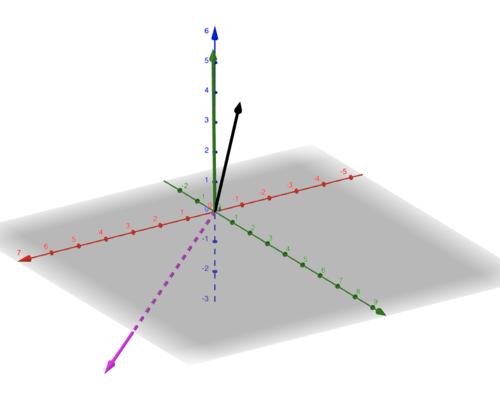
  ::在我告诉你这代表几何含义之前 让我们先看看几张计算图

  播放段落

  Here,  $\begin{array}{r}\stackrel{\to }{x}=\left[\begin{array}{c}1\\ 3\\ 5\end{array}\right]\text{ and }\stackrel{\to }{y}=\left[\begin{array}{c}2\\ 3\\ 7\end{array}\right]\text{ and }\stackrel{\to }{x}\times \stackrel{\to }{y}=\left[\begin{array}{c}6\\ 3\\ -3\end{array}\right]\end{array}$ .
  ::这里 x[135] 和y[237] 和xy[63-3]。

  

   

  播放段落

  and  $\begin{array}{r}\stackrel{\to }{x}\text{ is black, }\stackrel{\to }{y}\text{ is green and }\stackrel{\to }{x}\times \stackrel{\to }{y}\text{ is in pink. }\end{array}$  
  ::x是黑色的,y是绿色的, x是粉红色的。

  播放段落

  Another example has $\begin{array}{r}\stackrel{\to }{x}=\left[\begin{array}{c}1\\ -1\\ 1\end{array}\right],\stackrel{\to }{y}=\left[\begin{array}{c}-1\\ 2\\ -3\end{array}\right]\text{ and }\stackrel{\to }{x}\times \stackrel{\to }{y}=\left[\begin{array}{c}1\\ 2\\ 1\end{array}\right]\end{array}$  with the same color scheme as the previous example.
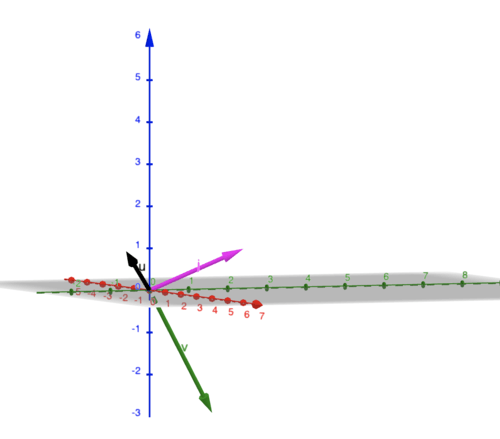
  ::与前一例相同颜色图案的Hasx[1-11]、y[-12-3]和xy[121]等例子。

  

  播放段落

  Now looking at both of these examples, the cross product is perpendicular to both of the vectors. And geometrically speaking, that is the definition. The cross product of two vectors in 3-dimensional space is the vector that is perpendicular to both. 
  ::以这两个例子来看,交叉产品与两个矢量是分不开的。从几何角度来说,这就是定义。三维空间中两个矢量的交叉产品与两个矢量是分不开的矢量。

  播放段落

  Now recalling the definition of the dot product geometrically,  $\begin{array}{r}\stackrel{\to }{x}\cdot \stackrel{\to }{y}=||\stackrel{\to }{x}||\cdot ||\stackrel{\to }{y}||\text{cos}(\theta )\end{array}$  thus when the two vectors are nonzero the dot product is 0 if and only the angle between them is  $\begin{array}{r}\frac{\pi }{2}\end{array}$  or they are perpendicular. Now checking these examples the dot product of each of the vectors with its cross product is 0.
  ::现在回顾点产物的几何定义, 因此当两个矢量为非零时, 点产物为 0, 如果它们之间的角为 +% 2 , 或者它们具有垂直性。 现在检查这些示例, 每个矢量的点产物及其交叉产物为 0 。

  播放段落

  And we can now show this from the general formula:
  ::现在我们可以从一般公式中显示这一点:

  播放段落

  $\begin{array}{r}\stackrel{\to }{x}\times \stackrel{\to }{y}=\left[\begin{array}{c}{x}_2{y}_3-x_3{y}_2\\ x_3{y}_1-x_1{y}_3\\ x_1{y}_2-x_2{y}_1\end{array}\right]\end{array}$  and  $\begin{array}{r}\stackrel{\to }{x}=\left[\begin{array}{c}{x}_1\\ x_2\\ x_3\end{array}\right]\text{ and }\stackrel{\to }{y}=\left[\begin{array}{c}{y}_1\\ y_2\\ y_3\end{array}\right]\end{array}$  so  $\begin{array}{r}(\stackrel{\to }{x}\times \stackrel{\to }{y})\cdot \stackrel{\to }{x}=\left[\begin{array}{c}{x}_2{y}_3-x_3{y}_2\\ x_3{y}_1-x_1{y}_3\\ x_1{y}_2-y_1{x}_2\end{array}\right]\cdot \left[\begin{array}{c}{x}_1\\ x_2\\ x_3\end{array}\right]=x_1(x_2{y}_3-x_3{y}_2)+x_2(x_3{y}_1-x_1{y}_3)+x_3(x_1{y}_2-y_1{x}_2)\end{array}$ . Now expanding out the equation comes to  $\begin{array}{r}(\stackrel{\to }{x}\times \stackrel{\to }{y})\cdot \stackrel{\to }{x}=x_1{x}_2{y}_3-x_1{x}_3{y}_2+x_2{x}_3{y}_1-x_1{x}_2{y}_3+x_1{x}_3-x_2{x}_3{y}_1\end{array}$  and then group like terms to get  $\begin{array}{r}(x_1{x}_2{y}_2-x_1{x}_2{y}_3)+(-x_1{x}_3{y}_2+x_1{x}_3{y}_2)+(x_2{x}_3{y}_1-x_2{x}_3{y}_1)=0\end{array}$ . Now it is required to show the same when applying the dot product to  $\begin{array}{r}\stackrel{\to }{y}.\end{array}$  
  ::{{{{{{{{{{{{{{{{{{{{{{{{{{{{{[x2x2x2x1}1x[x[x1xx2x3x3x3y3x3x3x2x3x3x3x3x3x3x1,1x3x1-x33x3x3x3x3-x33x2x3x2x3x3x3x3x3x3,1x2x3-3-3x3x3-x2x3-x3x3-x3-x3-x3-x3-x3-x3-x3x2x1和x[y2x,3xx3x3x3-3x3-3x3-x1-x1-x2-x2x2,[x1x1x1x2xxx2x2xxxx2,3x1, 和如此组等(x1x2x1)x1)x1+x1+x1(x1x2x2x1)+(x1-(x1x1-x3x3x3x3xxxxxx3x3x3x3-)+)+(x1x1x1x1-1x1x3-1xxxx3x3x3x3x3x1x1x1x1x1x1x1x1x1x1xxx1x1x1x1x1x1xxx1x1x1xx1x1x1x3x3x1x1x3xx3x3x3x3x3x3x3x3x3x3x3x3x3x3xxx3x3x3xxx3x1x3x1x1x1x1x1x1x1x1x1x1x1x1x3x3x3)+)+2)+(+2x1x1x1x1x1x1x1x1x1x1x1x1x1x1x1x1x1x

  播放段落

  $\begin{array}{r}(\stackrel{\to }{x}\times \stackrel{\to }{y})\cdot \stackrel{\to }{y}=\left[\begin{array}{c}{x}_2{y}_3-x_3{y}_2\\ x_3{y}_1-x_1{y}_3\\ x_1{y}_2-y_1{x}_2\end{array}\right]\cdot \left[\begin{array}{c}{y}_1\\ y_2\\ y_3\end{array}\right]=y_1(x_2{y}_3-x_3{y}_2)+y_2(x_3{y}_1-x_1{y}_3)+y_3(x_1{y}_2-y_1{x}_2)\end{array}$ . Then expanding out yields the equation  $\begin{array}{r}(\stackrel{\to }{x}\times \stackrel{\to }{y})\cdot \stackrel{\to }{x}=y_1{x}_2{y}_3-y_1{x}_3{y}_2+y_2{y}_1{x}_3-y_2{y}_3{x}_1+x_1{y}_2{y}_3-y_1{y}_3{x}_2.\end{array}$  Finally grouping together yields  $\begin{array}{r}(\stackrel{\to }{x}\times \stackrel{\to }{y})\cdot \stackrel{\to }{x}=(y_1{x}_2{y}_3-y_1{x}_2{y}_3)+(-y_1{x}_3{y}_2+y_2{y}_1{x}_3)+(y_2{y}_3{x}_1-y_2{y}_3{x}_1)=0\end{array}$ , proving that the cross product is orthogonal to the two vectors.
  :xy})

  播放段落

  Moving on, recall that the dot product had a formula in terms of direction and magnitude of the vectors, and likewise, the cross product does too.
  ::继续指出,圆点产品在矢量的方向和规模方面有一个公式,同样,交叉产品也有一个公式。

  播放段落

  $\begin{array}{r}||\stackrel{\to }{x}\times \stackrel{\to }{y}||=||\stackrel{\to }{x}||\cdot ||\stackrel{\to }{y}||\text{sin}(\theta )\text{ and }\stackrel{\to }{x}\times \stackrel{\to }{y}=||\stackrel{\to }{x}||\cdot ||\stackrel{\to }{y}||\text{sin}(\theta )\stackrel{\to }{v}\end{array}$  where  $\begin{array}{r}\stackrel{\to }{v}\end{array}$   is the unit vector going in the direction orthogonal to both  $\begin{array}{r}\stackrel{\to }{x}\text{ and }\stackrel{\to }{y}.\end{array}$  
  ::\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\ x\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\这个单位向向正正正正方向方向方向方向方向方向的单位向正方向方向方向的单位矢向方向方向方向的单位矢矢矢的矢矢矢矢矢矢矢矢的 xxxxxxxxxxxxxxxxxxxxxxxxxxxx\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\

  ---

  播放段落

  Proving this definition holds true is left as an exercise as well as showing these following identities:
  ::证明这一定义是真实的,留作一种练习,并显示以下身份:

  播放段落
  • $\begin{array}{r}\stackrel{\to }{x}\times \stackrel{\to }{x}=\stackrel{\to }{0}\end{array}$  
    ::{\fn黑体\fs22\bord1\shad0\3aHBE\4aH00\fscx67\fscy66\2cHFFFFFF\3cH808080}不! {\fn黑体\fs22\bord1\shad0\3aHBE\4aH00\fscx67\fscy66\2cHFFFFFF\3cH808080}不!
  播放段落
  • $\begin{array}{r}\stackrel{\to }{x}\times \stackrel{\to }{y}=-(\stackrel{\to }{y}\times \stackrel{\to }{x})\end{array}$  
    ::~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
  播放段落
  • $\begin{array}{r}\hat{i}\times \hat{j}=\hat{k},\hat{i}\times \hat{k}=\hat{j}\text{ and }\hat{j}\times \hat{k}=\hat{i}\end{array}$
    ::~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~
  播放段落
  • $\begin{array}{r}\stackrel{\to }{x}\times (\stackrel{\to }{y}+\stackrel{\to }{z})=\stackrel{\to }{x}\times \stackrel{\to }{y}+\stackrel{\to }{x}\times \stackrel{\to }{z}\end{array}$  
    ::
  播放段落
  • $\begin{array}{r}(\stackrel{\to }{x}\times \stackrel{\to }{y})\times \stackrel{\to }{z}\ne \stackrel{\to }{x}\times (\stackrel{\to }{y}\times \stackrel{\to }{z})\end{array}$
    :x ) ) )
  播放段落
  • And lastly,  $\begin{array}{r}k,(k\stackrel{\to }{x})\times \stackrel{\to }{y}=\stackrel{\to }{x}\times (k\stackrel{\to }{y})=k(\stackrel{\to }{x}\times \stackrel{\to }{y})\end{array}$    
    ::最后, k, (kx}) ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

  ---

   

  播放段落

  Now,  watch  these other videos to help your understanding:
  ::现在,看这些其他视频 帮助您理解:

  播放段落

  This video helps you conceptually understand the cross product a bit better:
  ::这段视频能帮助您在概念上更好地理解交叉产品: