1.6 预测

Section outline

• Select section General

  Collapse Expand

  General

  Collapse all Expand all

  • Select activity 新闻通告

    

    新闻通告 Forum
• Select section 预测预测数

  Collapse Expand

  预测预测数

  播放段落

  In this lesson we will introduce a new topic of projection vectors. When we project one vector onto another, it is exactly what it sounds like, we extend the first vector and drop a perpendicular onto the line of the second vector in order to see what the image of the vector would look like if we placed it on the other vector.
  ::在此教训中, 我们将引入一个新的投影矢量主题 。 当我们将一个矢量投射到另一个矢量时, 这正是它听起来的样子, 我们扩展第一个矢量, 然后将一个垂直的矢量投到第二个矢量的线上, 以便看看如果把它放到另一个矢量上, 该矢量的图像会是什么样子 。

  ---

  播放段落

  Let's try and visualize this image:
  ::让我们试着想象一下这幅图象:

   

  播放段落

  When we project the top vector onto the bottom vector, we get this:
  ::当我们将上向矢量投射到下向量时, 我们得到这个:

  播放段落

  The red line, which is a scalar multiple of the bottom vector is what we get when we project the top vector onto the bottom one.
  ::红线,是底向量的斜线倍数 当我们将顶向量投射到底向量时,我们得到的就是它。

  播放段落

  Intuitively, this should make sense, you are dropping a perpendicular and then finding the proper scalar multiple.
  ::直观地说,这应该有道理, 你正在抛下一个垂直的直角 然后找到适当的天平倍数。

  ---

   

  播放段落

  Let's look at a few more examples:
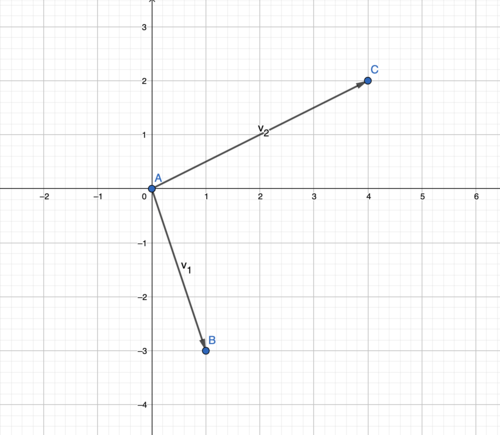
  ::让我们再举几个例子:

  播放段落

  Take the vectors
  ::选择矢量

  播放段落

  $\begin{array}{r}\stackrel{\to }{v_1}=\left[\begin{array}{c}2\\ 1\end{array}\right]\\ \stackrel{\to }{v_2}=\left[\begin{array}{c}3\\ 5\end{array}\right]\end{array}$
  ::v1[21]v2}[35]

  播放段落

  We can see that the red vector on the bottom becomes the projection
  ::我们可以看到,最下面的红矢量 变成了投影

  播放段落

  As we can see here the bottom vector is shorter than the top vector so the projection because a larger scalar multiple to fit the projection.
  ::正如我们在这里所看到的, 底层矢量比顶层矢量短, 所以投影是因为要有一个更大的标量倍数来适应投影。

  播放段落

  Looking at the value of the vector, we see that it is  $\begin{array}{r}\left[\begin{array}{c}\frac{68}{11}\\ \frac{34}{11}\end{array}\right]\end{array}$
  ::从矢量的价值来看,我们看到矢量的价值是[68113411]

  ---

   

  播放段落

  Looking at a further example we get 
  ::研究我们得到的又一例子

  播放段落

  Again, when we drop a perpendicular from the green vector onto the purple vector we then get the blue vector as the projection. 
  ::当我们再次从绿色矢量向紫矢量投下垂直垂直时, 我们就会得到蓝色矢量作为投影。

  ---

   

  播放段落

  So hence, given
  ::因此,因此,

  播放段落

  $\begin{array}{r}\stackrel{\to }{v_1}=\left[\begin{array}{c}-1\\ 2\end{array}\right]\\ \stackrel{\to }{v_2}=\left[\begin{array}{c}4\\ 5\end{array}\right]\end{array}$
  ::v1[- 12]v2}[45]

  播放段落

  and the projection vector becomes the vector 
  ::投影矢量成为矢量

  播放段落

  $\begin{array}{r}pro{j}_{\stackrel{\to }{v_1}}\stackrel{\to }{v_2}=\left[\begin{array}{c}\frac{25}{6}\\ \frac{10}{3}\end{array}\right]\end{array}$
  ::[256103]

  ---

   

  播放段落

  Now, let's try and generalize this and prove the formula for the projection vector.
  ::现在,让我们试着概括一下这个, 并证明投影矢量的公式。

  播放段落

  We know that given any two vectors   $\begin{array}{r}\stackrel{\to }{v_1},\stackrel{\to }{v_2}\end{array}$  the projection of  $\begin{array}{r}\stackrel{\to }{v_2}\end{array}$  onto  $\begin{array}{r}\stackrel{\to }{v_1}\end{array}$ , denoted by  $\begin{array}{r}pro{j}_{\stackrel{\to }{v_1}}\stackrel{\to }{v_2}\end{array}$  is going to be a scalar multiple of  $\begin{array}{r}\stackrel{\to }{v_1}\end{array}$  
  ::我们知道,鉴于任何两种矢量 v1,v2,V2对 v1的投影, 以projv1v2的表示, 将会是 v1的螺旋倍数。

  播放段落

  So it will have the direction of the  first vector and thus we can write that
  ::因此,它将具有第一个向向向的方向, 因此我们可以写下

  播放段落

  $\begin{array}{r}pro{j}_{\stackrel{\to }{v_1}}\stackrel{\to }{v_2}=c\cdot \stackrel{\to }{v_1}\end{array}$  
  ::

  播放段落

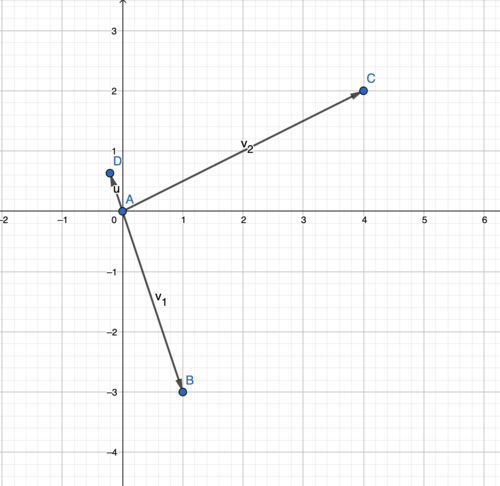
  Now, let's look at the picture of this
  ::现在,让我们看看这个图片

   

  

   

   

  播放段落

  We can see that point D is  $\begin{array}{r}pro{j}_{\stackrel{\to }{v_1}}\stackrel{\to }{v_2}\end{array}$
  ::我们可以看到D点是projv1v2

  播放段落

  So, we can gather that if we take the vector u (the perpendicular) and add it to the projection we get
  ::所以,我们可以收集到 如果我们采取矢量 u(直视) 并加入到投影中

  播放段落

  $\begin{array}{r}pro{j}_{\stackrel{\to }{v_1}}\stackrel{\to }{v_2}+\stackrel{\to }{u}=\stackrel{\to }{v_2}\end{array}$
  ::-=YTET -伊甸园字幕组=-伊甸园字幕组=-伊甸园字幕组=-伊甸园字幕组=-伊甸园字幕组=-伊甸园字幕组=-伊甸园字幕组=-伊甸园字幕组=-伊甸园字幕组=-伊甸园字幕组=-伊甸园字幕组=-伊甸园字幕组=-伊甸园字幕组=-伊甸园字幕组=-伊甸园字幕组=-伊甸园字幕组=-伊甸园字幕组=- 翻译:

  播放段落

  So
  ::苏

  播放段落

  $\begin{array}{r}\stackrel{\to }{v_2}=c\stackrel{\to }{v_1}+\stackrel{\to }{u}\\ \stackrel{\to }{v_1}\cdot \stackrel{\to }{v_2}=(c\stackrel{\to }{v_1}+\stackrel{\to }{u})\cdot \stackrel{\to }{v_1}\\ \stackrel{\to }{v_1}\cdot \stackrel{\to }{v_2}=c\stackrel{\to }{v_1}\cdot \stackrel{\to }{v_1}+\stackrel{\to }{u}\cdot \stackrel{\to }{v_1}\\ \stackrel{\to }{v_1}\cdot \stackrel{\to }{v_2}=c\stackrel{\to }{v_1}\cdot \stackrel{\to }{v_1}\\ \stackrel{\to }{v_1}\cdot \stackrel{\to }{v_2}=c||\stackrel{\to }{v_1}|{|}^2\\ \text{so we can get }c\text{ as}\\ c=\frac{\stackrel{\to }{v_1}\cdot \stackrel{\to }{v_2}}{||\stackrel{\to }{v_1}|{|}^2}\end{array}$
  ::{\fn黑体\fs22\bord1\shad0\3aHBE\4aH00\fscx67\fscy66\2cHFFFFFF\3cH808080}... {\fn黑体\fs22\bord1\shad0\3aHBE\4aH00\fscx67\fscy66\2cHFFFFFF\3cH808080}... {\fn黑体\fs22\bord1\shad0\3aHBE\4aH00\fscx67\fscy66\2cHFFFFFF\3cH808080}... {\fn黑体\fs22\bord1\shad0\3aHBE\4aH00\fscx67\fscy66\2cHFFFFFF\3cH808080}... {\fn黑体\fs22\bord1\shad0\3aHBE\4aH00\fscx67\fscy66\2cHFFFFFF\3cH808080}... {\fn黑体\fs22\bord1\shad0\3aHBE\4aH00\fscx67\fscy66\2cHFFFFFF\3cH808080}...

  播放段落

  Now we get that
  ::瞷и瞷笵

  播放段落

  $\begin{array}{r}pro{j}_{\stackrel{\to }{v_1}}\stackrel{\to }{v_2}=\frac{\stackrel{\to }{v_1}\cdot \stackrel{\to }{v_2}}{||\stackrel{\to }{v_1}|{|}^2}\stackrel{\to }{v_1}\end{array}$
  ::

  播放段落

  So now we have the formula for a projection vector.
  ::现在我们有了投影矢量的公式

  ---

   

  播放段落

  So now let's try out a few examples:
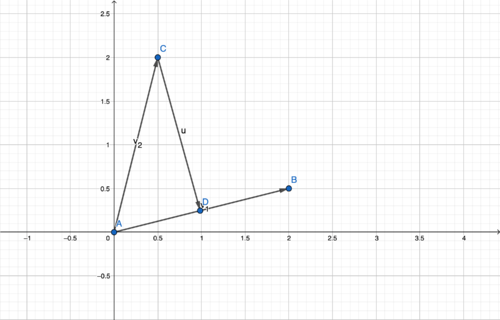
  ::现在让我们举几个例子:

  播放段落

  Example 1: Calculate the projection vector of  $\begin{array}{r}\stackrel{\to }{v_1}=\left[\begin{array}{c}1\\ -3\end{array}\right]\end{array}$  and  $\begin{array}{r}\stackrel{\to }{v_2}=\left[\begin{array}{c}4\\ 2\end{array}\right]\end{array}$  
  ::示例1:计算 v1[1-3] 和 v2[42] 的投影矢量

  播放段落

  Here's a picture of these two vectors:
  ::以下是这两条矢量的图片:

   

  

   

   

  播放段落

  Calculating the projection vector we get:
  ::计算我们得到的投影矢量:

  播放段落

  $\begin{array}{r}\stackrel{\to }{v_1}\cdot \stackrel{\to }{v_2}=\left[\begin{array}{c}1\\ -3\end{array}\right]\cdot \left[\begin{array}{c}4\\ 2\end{array}\right]\\ =4(1)+2(-3)\\ =4-6\\ =-2\end{array}$  
  
  ::[1-3][42]=4(1)+2(-3)=4-62]

  播放段落

  Then,  $\begin{array}{r}||\stackrel{\to }{v_1}|{|}^2=||<1,-3>|{|}^2={\sqrt{1^2+(-3{)}^2}}^2={\sqrt{10}}^2=10\end{array}$
  ::然后,#v121,-32=12+(-3)22=102=10

  播放段落

  So scaling  $\begin{array}{r}\stackrel{\to }{v_1}\end{array}$  by  $\begin{array}{r}\frac{-2}{10}=\frac{-1}{5}\end{array}$  we get
  ::因此,通过 - 210\\\\\15 来缩放 v1

  播放段落

  $\begin{array}{r}-\frac{1}{5}\stackrel{\to }{v_1}=\left[\begin{array}{c}-\frac{1}{5}\\ \frac{3}{5}\end{array}\right]\end{array}$
  ::-15v1[-535]

  播放段落

  So,
  ::那么,

  播放段落

  $\begin{array}{r}\stackrel{\to }{v_1}=\left[\begin{array}{c}1\\ -3\end{array}\right]\\ \stackrel{\to }{v_2}=\left[\begin{array}{c}4\\ 2\end{array}\right]\\ pro{j}_{\stackrel{\to }{v_1}}\stackrel{\to }{v_2}=\left[\begin{array}{c}-\frac{1}{5}\\ \frac{3}{5}\end{array}\right]\end{array}$
  ::[1-3]v2][42]projv1}v2}[-1535]

  播放段落

  And this is what the diagram of the projection vector with the first two vectors look like
  ::这是前两个矢量的投影矢量图

   

  

   

   

  播放段落

  Now that we've seen how it works visually let's just brute force out these calculations in the next few examples and check to see if the results we get make sense.
  ::现在我们已经看到它如何在视觉上运作了 让我们在接下来的几个例子中 大力推出这些计算 并检查一下结果是否合情合理

  ---

  播放段落

  Example 2:   Calculate the projection vector of  $\begin{array}{r}\stackrel{\to }{v_1}=\left[\begin{array}{c}-4\\ 5\end{array}\right]\end{array}$  and  $\begin{array}{r}\stackrel{\to }{v_2}=\left[\begin{array}{c}-2\\ \frac{1}{3}\end{array}\right]\end{array}$
  
  ::示例2:计算 v1[-45] 和 v2[-213] 的预测矢量

  播放段落

  $\begin{array}{r}pro{j}_{\stackrel{\to }{v_1}}\stackrel{\to }{v_2}=\frac{\stackrel{\to }{v_1}\cdot \stackrel{\to }{v_2}}{||\stackrel{\to }{v_1}|{|}^2}\stackrel{\to }{v_1}\end{array}$  
  
  ::

  $\begin{array}{r}\frac{\left[\begin{array}{c}-4\\ 5\end{array}\right]\cdot \left[\begin{array}{c}-2\\ \frac{1}{3}\end{array}\right]}{||\left[\begin{array}{c}-4\\ 5\end{array}\right]|{|}^2}\\ =\\ \frac{(-4)(-2)+(5)(\frac{1}{3})}{(\sqrt{(-4{)}^2+5^2}{)}^2}\\ =\\ \frac{8+\frac{5}{3}}{(\sqrt{41}{)}^2}\\ =\\ \frac{\frac{29}{3}}{41}\\ =\\ \frac{29}{123}\end{array}$  
  

  播放段落

  So we get the projection to be 
  ::因此,我们得到的预测是

  $\begin{array}{r}\left[\begin{array}{c}-\frac{92}{129}\\ \frac{105}{129}\end{array}\right]\end{array}$  
  

  ---

  播放段落

  Here are a few videos for you help develop your understanding of vector projections.
  ::以下是一些视频,供您帮助培养您对矢量预测的理解。