Course: 2.1 线性赤道系统

Section outline

Select section General

Collapse Expand
General

Collapse all Expand all
- Select activity 新闻通告
  
  新闻通告 Forum
Select section 赤道线性系统

Collapse Expand
赤道线性系统
You probably remember them from high school or middle school math, but linear systems equations are actually the basis of all of linear algebra.
::你可能记得高中或中学数学中的数学, 但线性系统方程式其实是所有线性代数的基础。

Let's try out an example:
::让我们举个例子:

$\begin{align*} 3x + 2y = 1\\ 4x + 5y = 2\end{align*}$
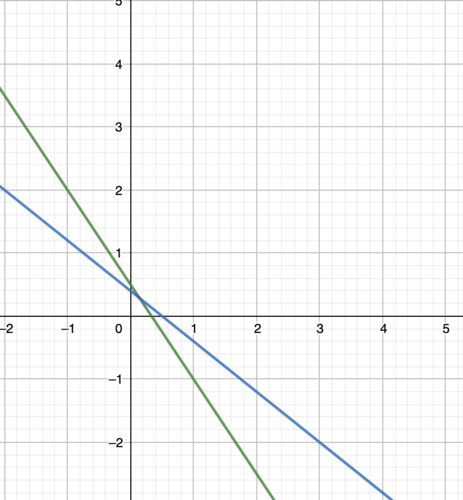
::3x+2y=14x+5y=2

For this problem let's use the method of substitution and solve the first equation for $\begin{align*}x\end{align*}$ in terms of $\begin{align*}y.\end{align*}$ $\begin{align*}x = \frac{1}{3} - \frac{2}{3}\cdot y\end{align*}$ and plug in to the second equation to get $\begin{align*}\frac{4}{3} - \frac{8}{3}y + 5y = 2\end{align*}$ so $\begin{align*}\frac{2}{3} = \frac{7}{3}y, y = \frac{2}{7}\end{align*}$ . Now, plugging the y back in to solve for x you get $\begin{align*}x = \frac{1}{3} - \frac{4}{21} = \frac{1}{7}\end{align*}$ and our solution is $\begin{align*}(\frac{1}{7},\frac{2}{7}).\end{align*}$
::对于这个问题,让我们使用替代方法, 解决 x 的第一个方程式, 以y. x= 13 - 23y 和插插插到第二个方程式中, 以获得 43 - 83y+5y=2 so 23= 73y,y=27。现在, 插入 y 以解答 x 的 x = 13 - 421=17, 我们的解决方案是 (17, 27) 。

This linear system had one solution and is called consistent . We can further verify this by looking at the graph of the two lines.
::这个线性系统有一个解决方案, 并被称为一致。我们可以通过查看两条线的图表来进一步验证这一点。

However, an inconsistent system is a system of equations that has no solutions, or where the lines are parallel:
::然而,一个不一致的系统是没有解决办法的方程式系统,或线条平行的方程式系统:

Here you can see that there are no solutions and geometrically this means the lines have the same .
::这里你可以看到没有解决办法, 从几何角度来说,这意味着线条是相同的。

However, when the lines are the same we say there are infinitely many solutions and represent the solution set as   $\begin{align*}\begin{bmatrix}y\\x\end{bmatrix} = \begin{bmatrix}ax+b\\x\end{bmatrix} = x\begin{bmatrix}a\\1\end{bmatrix} + \begin{bmatrix}b\\0\end{bmatrix}\end{align*}$ .
::然而,当线条相同时,我们说有无限多的解决方案,它代表了设定为[yx]=[xx+bx]=x[a1]+[b0]的解决方案。

Example 1
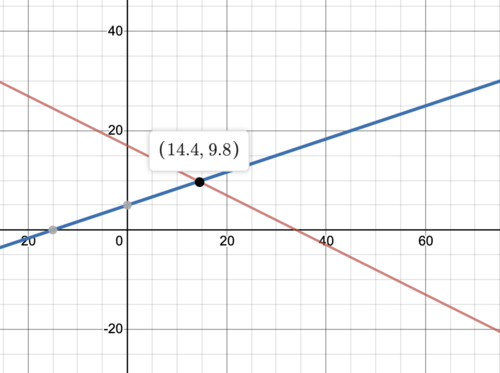
::例1

Find the solution set to the system of linear equations
::为线性方程式系统找到设定的解决方案

$\begin{align*}y = \frac{1}{3}x + 5 \\ y = -\frac{1}{2}x + 17\end{align*}$
::y= 13x+5y @ 12x+17

Solve to get
::解决获得

$\begin{align*}-\frac{1}{2}x + 17 = \frac{1}{3}x + 5 \\ -\frac{1}{2}x + 12 = \frac{1}{3}x \\ 12 = \frac{1}{2}x + \frac{1}{3}x \\ \frac{1}{2}x + \frac{1}{3}x = 12 \\ \big(\frac{1}{2} + \frac{1}{3}\big)x = 12 \\ \big(\frac{5}{6}\big)x = 12 \\ x = \frac{6}{5}\cdot 12 \\ x = \frac{72}{5} = 14.4\end{align*}$
::− 12x+17=13x5-12x+12=13x12=12x13x12x13x13x12(12+13x13x)12x12(12+13)x12(56)x=12x=12x=65=12x=725=14.4

Plugging back in we get $\begin{align*}y = 9.8\end{align*}$
::我们得到y=9.8的Y=9.8

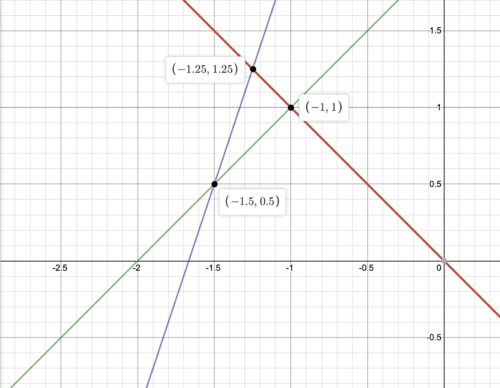
Let's try another example:
::让我们尝试另一个例子:

$\begin{align*}3x+4y = -1\\ 5x - 4y = 2\end{align*}$
::3x+4y 15x-4y=2

Now we can use the method of elimination and add the two equations together (which preserves the properties needed) to get
::现在,我们可以使用消除方法,把两个方程加在一起(这保留了所需的属性),以获得

$\begin{align*}8x = 1 \\ x = \frac{1}{8}\end{align*}$
::8x=1x=18

Then we can plug back in to either equation to solve for y now that we have our answer for x.
::然后,我们可以插回任何一种方程式解决y,现在,我们得到了我们的答案x。

$\begin{align*}\frac{3}{8} + 4y = -1 \\ 4y = -\frac{11}{8} \\ y = -\frac{11}{32}\end{align*}$
::38+4y14y118y1132

Now let's look at systems with three or more linear equations:
::现在让我们看看三个或三个以上线性方程式的系统:

$\begin{align*}y=-x\\ y=x+2\\ y=3x+5\\\end{align*}$
::yxy=x+2y=3x+5

There is no common solution to these system of equations, both algebraically and geometrically. This is an inconsistent system.
::这些方程式系统在代数和几何两个方面都没有共同的解决办法,这是一个不一致的系统。

The two dimensional systems of linear equations are kind of boring so we can move on to systems with more variables.
::线性方程式的两维系统有点无聊这样我们就可以进入具有更多变量的系统

Let's take this 3x3 system of equations:
::让我们用3x3的方程式系统:

$\begin{align*}3x_{1} + 4x_{2} + 7x_{3} = 1 \\ 2x_{1} - 5x_{2} + 8x_{3} = 3 \\ \frac{3}{2}x_{1} - \frac{4}{5}x_{2} + x_{3} = -2 \end{align*}$
::3x1+4x2+7x3=12x1-5x2+8x3=332x1-45x2+x3=2

To solve this we will use an analogue of what we have used to solve systems of two variables. First let's multiply the bottom equation by 10 to clear the fractions.
::为了解决这个问题,我们将使用我们用来解答两个变量系统的类比。首先,让我们将底方程乘以 10 来清除分数。

Now our system has become
::现在,我们的系统已经变成

$\begin{align*}3x_{1} + 4x_{2} + 7x_{3} = 1 \\ 2x_{1} - 5x_{2} + 8x_{3} = 3 \\ 15x_{1} - 8x_{2} + 10x_{3} = -20 \end{align*}$
::3x1+4x2+7x3=12x1-5x2+8x3=315x1-8x2+10x3=20

First, multiply the first equation by -5 and add that to the third equation turning the third equation of the system into
::首先,将第一个方程乘以 - 5, 并加上, 在第三个方程中, 将系统第三个方程转换为

$\begin{align*}-28x_{2} - 25x_{3} = -25\to 28x_{2} + 25x_{3} = 25\end{align*}$
::- 28x2-25x325_28x2+25x3=25

Now let's do a similar process, but onto the second row. So we multiply the first equation by -2/3 and then add that to the second equation transforming the second equation to:
::现在让我们做一个类似的进程, 但是在第二行上。所以我们将第一个方程乘以 - 2/3, 然后在第二个方程中加入这个, 然后将第二个方程转换为:

$\begin{align*}-\frac{23}{3}x_{2} + \frac{10}{3}x_{3} = \frac{7}{3} \to -23x_{2} + 10x_{3} = 7\end{align*}$
::-233x2+103x3=7323x2+10x3=7

Now our system is
::现在我们的系统是

$\begin{align*}3x_{1} + 4x_{2} + 7x_{3} = 1 \\ -23x_{2} + 10x_{3} = 7\\ 28x_{2} + 25x_{3} = 25 \end{align*}$
::3x1+4x2+7x3=1-23x2+10x3=728x2+25x3=25

The multiply the second equation by 28/23 and then add it to the third equation transforming the third equation to
::乘以第二个方程乘以28/23,然后加到第三个方方程中,将第三个方方程转换为

$\begin{align*}\frac{152}{23}x_{3} = \frac{771}{23}\end{align*}$
::15223x3=77123

Then we can solve for $\begin{align*}x_{3}\end{align*}$ getting
::然后我们就可以解决 X3 获得

$\begin{align*}\frac{771}{152}\end{align*}$

Now let's plug back in to the system of equations and solve for $\begin{align*}x_{1}\end{align*}$ and $\begin{align*}x_{2}\end{align*}$ , so
::现在让我们连接到方程系统并解析 x1 和 x2, 所以

$\begin{align*}-23x_{2} + 10(\frac{771}{152}) = 7 \\ -23x_{2} = 7 - \frac{7710}{152} = -\frac{6646}{152} = -\frac{3323}{76} \\ x_{2} = \frac{3323}{1748}\end{align*}$
::-23x2+10(771152)=7-23x2=7-7710152_6646152_332376x2=33231748

Plugging back in again to solve for $\begin{align*}x_{1}\end{align*}$ we get $\begin{align*}3x_{1} + 4x_{2} + 7x_{3} = 1 \\ 3x_{1} + 4(\frac{3323}{1748}) + 7(\frac{771}{152}) = 1 \\ 3x_{1} = 1 - 4(\frac{3323}{1748}) - 7(\frac{771}{152})\\ 3x_{1} = -\frac{147219}{3496}\\ x_{1} = -\frac{147219}{10488}\\ \end{align*}$
::重新插入以解析 x1 我们得到 3x1+4x2+7x3=13x1+4(33231748)+7(771152)=13x1=1-4(33231748)-7(771152)3x1=1-7(771152)3x11472193496x114721910488

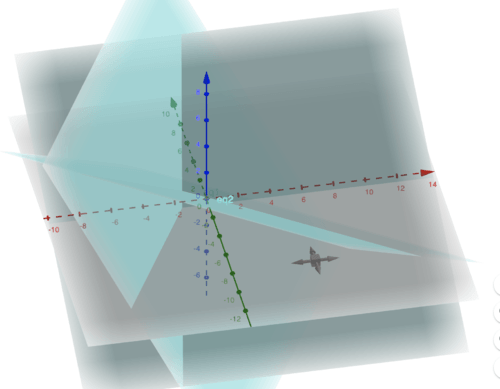
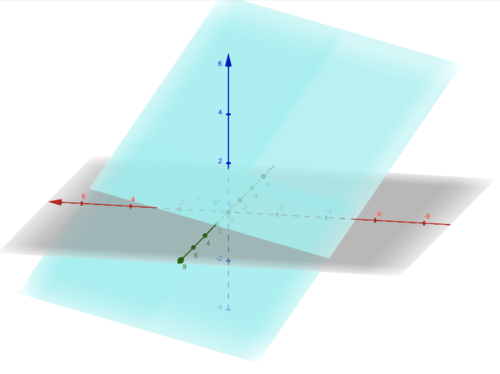
Analyzing this geometrically we get three planes intersecting at a point:
::以几何方式分析我们得到三架飞机在一个点交叉:

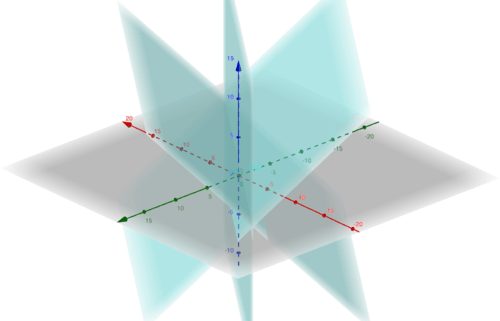
This was a good example of a consistent system with one solution, now let's look at one with infinite solutions.

Recall that in one dimensions there were infinite solutions when we had two identical lines. Now in 3d this is the case with 3 identical planes or two planes intersecting and one going through the line of intersection which works because two planes intersect at a line.

Take these two systems as an example:

1. $\begin{align*}3x_{1} + 4x_{2} + 5x_{3} = 9 \\ 9x_{1} + 12x_{2} + 15x_{3} = 27 \\ -3x_{1} - 4x_{2} - 5x_{3} = -9\end{align*}$

Here all of these planes are the same because they are just scalar multiples of each other and they are all going into the same direction.

Looking here we have the picture:
::看看这里,我们有一张图片:

Because all these planes are equal let's just represent this as the plane from the first equation of $\begin{align*}3x_{1} + 4x_{2} + 5x_{3} = 9\end{align*}$ . Even though there are infinite solutions we should write the general form of the solutions where we can say   $\begin{align*}x_{1} = \frac{1}{3}(-4x_{2} - 5x_{3} + 9)\end{align*}$ and then because x1 is the only one of these variables whose value is dependent on something we call the other two variables x2 and x3 to be free variables as they are independent .
::因为所有这些平面都是相等的, 让我们将它作为第一个方程的平面来表示, 3x1+4x2+5x3=9. 尽管有无限的解决方案, 我们应该写出一般的解决方案形式, 在那里我们可以说 x1=13( 4x2- 5x3+9) , 然后因为 x1 是这些变量中唯一一个其价值取决于我们称之为其他两个变量 x2 和 x3 的变量的变量, 它们是独立的。

Now we could also write the solution set as $\begin{align*}x_{2}\end{align*}$ in terms of $\begin{align*}x_{1}\end{align*}$ and $\begin{align*}x_{3}\end{align*}$ and then $\begin{align*}x_{1}\end{align*}$ and $\begin{align*}x_{3}\end{align*}$ are called free. So free variables just depend on how you write the solution set and the solution set is usually written as the first variable in terms of the rest. However, you will not need this convention for long when we learn parametric vector form.
::现在,我们也可以以 x1 和 x3 来写入设定为 x2 的溶液, 然后将 x1 和 x3 称为自由。因此, 自由变量仅取决于您如何写入解决方案集, 而设定的溶液通常作为其它变量的第一个变量写入。但是, 当我们学习参数矢量表时, 您不需要这个常规。

Now let's go to the second case. This is when we had three planes in a line.
::现在让我们来谈第二个案子。这是我们有三架飞机排队的时候。

In this example we had the equations
::在这个例子中,我们有方程式

$\begin{align*}3x_{1} + 4x_{2} + 5x_{3} = 9 \\ -3x_{1} - 4x_{2} + 5x_{3} = 9 \\ \frac{3}{4}x_{1} + x_{2} + 0x_{3} = 0 \end{align*}$
::3x1+4x2+5x3=9-3x1-4x2+5x3=9-4x3=9-4x1+934x1+x2+0x3=0

The three of these intersect in a line where when adding the two equations together we get $\begin{align*}x_{3} = \frac{9}{5}\end{align*}$ and $\begin{align*}x_{1} = -\frac{4}{3}x_{2}\end{align*}$ and then we have $\begin{align*}x_{2}\end{align*}$ as a free variable.
::其中三个相交于一条线, 当将两个方程式加在一起时, 我们得到 x3=95 和 x1\43x2, 然后我们得到 x2 作为自由变量。

Now, we have seen cases of when solutions are consistent with only one solution, inconsistent or consistent with infinitely many solutions.
::现在,我们看到一些情况,即解决办法只符合一种解决办法,不符合或符合无穷无尽的多种解决办法。

We can actually look at this in terms of span and linear combinations of vectors. With a system of linear equations you are essentially taking the span of the column vectors for each of the respective variables and finding the solution vector in the span. You can also look into the geometry of the span using plane geometry.
::我们实际上可以从矢量的跨度和线性组合的角度来看待这个问题。通过一个线性方程系统,您将基本上对每个变量的柱矢量的宽度进行计算,并在宽度中找到解析矢量。您也可以使用平面几何来查看跨度的几何。

When there are no solutions we see that the vector is not in the span of the columns (and if there are 3 vectors, then the vectors are linearly independent , why is that not necessarily true if there are less than 3? ) or that the planes do not intersect at one common point (i.e., they could be parallel or they could intersect with each other just all at different points).
::当没有解决办法时,我们看到矢量不在柱体范围内(如果有3个矢量,那么矢量是线性独立的,那么如果少于3个矢量,为什么不一定是真实的?),或者在一个共同点(即它们可能是平行的,或者它们可以在不同点相互交叉),平面没有交叉。

When there are infinitely many solutions, the planes either intersect at a line or are all the same plane. In terms of span, the vectors are linearly independent and then you can find a relationship in terms of the variables such that one variable is free and thus there are infinitely many solutions.
::当有无限多的解决方案时, 平面要么在直线上交叉, 要么都是相同的平面。在横线上, 矢量是线性独立的, 然后您就可以从变量中找到一种关系, 这样一个变量是自由的, 因此有无限多的解决方案。

Lastly when there is one and only one solution we have that three planes are intersecting at a point or the set of vectors are linearly independent and furthermore , the vector you are solving for is in the span of the 3 vectors.
::最后,当我们有一个唯一的解决方案, 即三平面在一个点交叉, 或者一组矢量是线性独立的, 此外, 您正在解决的矢量是在 3 个矢量的间距。

Section outline

General

赤道线性系统