课程： 2.2 减少行数 | The Way To Learn

章节大纲

选择节常规

折叠展开
常规

全部折叠展开全部
- 选择活动新闻通告
  
  新闻通告讨论区
选择节缩排

折叠展开
缩排
In the last lesson while we were solving systems of linear equations we used a process called elimination. First, we would try to get rid of the $\begin{aligned} x_{1} \end{aligned}$ terms in the second and third equations (while solving a three variable system) then we would solve a simpler system for the next two equations in terms of the $\begin{aligned} x_{2} \end{aligned}$ and $\begin{aligned} x_{3} \end{aligned}$ variables where we used a similar method of removing the $\begin{aligned} x_{2} \end{aligned}$ term from the third equation and then solving for $\begin{aligned} x_{3} \end{aligned}$ . And finally we would plug back in for $\begin{aligned} x_{2} \end{aligned}$ and then for $\begin{aligned} x_{1} \end{aligned}$ in order to entirely solve the system.
::在最后的教训中,当我们解决了线性方程式系统时,我们用了一个叫做消除的过程。首先,我们试图消除第二和第三方程式中的 x1 术语(同时解决三个变量系统),然后我们用一个类似的方法,从第三个方程式中去掉 x2 术语,然后解决 x3 。最后,我们再插入 x2,然后是 x1,以便完全解决这个系统。

Now recall that we talked about how we could look at these systems of linear equations as basically linear combinations of vectors formed by the variable coefficients, so for example solving
::现在记得,我们曾讨论过如何将这些线性方程式系统视为由可变系数构成的矢量基本上线性组合,例如,解决

$\begin{aligned} a_{1} x_{1} + b_{1} x_{2} + c_{1} x_{3} = d_{1} \\ a_{2} x_{1} + b_{2} x_{2} + c_{2} x_{3} = d_{2} \\ a_{3} x_{1} + b_{3} x_{2} + c_{3} x_{3} = d_{3} \end{aligned}$
::a1x1+b1x2+c1x3=d1a2x1+b2x2+c2x3=d2a3x1+b3x2+c3x3=d3

is the same as solving
::与解决相同

$\begin{aligned} [\begin{matrix} a_{1} \\ a_{2} \\ a_{3} \end{matrix}] x_{1} + [\begin{matrix} b_{1} \\ b_{2} \\ b_{3} \end{matrix}] x_{2} + [\begin{matrix} c_{1} \\ c_{2} \\ c_{3} \end{matrix}] x_{3} = [\begin{matrix} d_{1} \\ d_{2} \\ d_{3} \end{matrix}] \end{aligned}$
::[a1a2a3]x1+[b1b2b3]x2+[c1c2c3]x3=[d1d2d3]

When we thought about this geometrically we looked at this as if we were taking $\begin{aligned} Span {[\begin{matrix} a_{1} \\ a_{2} \\ a_{3} \end{matrix}], [\begin{matrix} b_{1} \\ b_{2} \\ b_{3} \end{matrix}], [\begin{matrix} c_{1} \\ c_{2} \\ c_{3} \end{matrix}]} \end{aligned}$
::当我们从几何角度考虑这个时, 我们把这看得好像我们在采取Span{[a1a2a3],[b1b2b3],[c1c2c3]}

and checking if
::检查是否

$\begin{aligned} [\begin{matrix} d_{1} \\ d_{2} \\ d_{3} \end{matrix}] \in Span {[\begin{matrix} a_{1} \\ a_{2} \\ a_{3} \end{matrix}], [\begin{matrix} b_{1} \\ b_{2} \\ b_{3} \end{matrix}], [\begin{matrix} c_{1} \\ c_{2} \\ c_{3} \end{matrix}]} \end{aligned}$
::[d1d2d3]span{[a1a2a3],[b1b2b3],[c1c2c3]}

and if so what linear combination of the vectors it is. We had a variety of different cases to check and linear dependence and independence relations to show and what not.
::如果是这样的话, 矢量的线性组合是什么。我们有很多不同的案例要检查,线性依赖和独立关系来显示和不显示。

Looking at the vector equation and recalling our matrix multiplication skills we see that $\begin{aligned} [\begin{matrix} a_{1} \\ a_{2} \\ a_{3} \end{matrix}] x_{1} + [\begin{matrix} b_{1} \\ b_{2} \\ b_{3} \end{matrix}] x_{2} + [\begin{matrix} c_{1} \\ c_{2} \\ c_{3} \end{matrix}] x_{3} = [\begin{matrix} a_{1} & b_{1} & c_{1} \\ a_{2} & b_{2} & c_{2} \\ a_{3} & b_{3} & c_{3} \end{matrix}] \cdot [\begin{matrix} x_{1} \\ x_{2} \\ x_{3} \end{matrix}] = [\begin{matrix} d_{1} \\ d_{2} \\ d_{3} \end{matrix}] \end{aligned}$ and this is called the matrix vector equation of the system of linear equations which we will talk more about later. You can compact this equation into what we call an augmented matrix of the form $\begin{aligned} [A | \vec{b}] \end{aligned}$ or in our case $\begin{aligned} [\begin{matrix} a_{1} & b_{1} & c_{1} ∣ d_{1} \\ a_{2} & b_{2} & c_{2} ∣ d_{2} \\ a_{3} & b_{3} & c_{3} ∣ d_{3} \end{matrix}] \end{aligned}$ .
::查看矢量方程并忆及我们的矩阵乘法,我们看到[a1a2a3]x1+[b1b2b3]x2+[c1c2c3]x3=[a1b1c1c2b2c2c3]{[x1x2x3]=[d1d2d3]],这被称为线性方程系统中的矩阵矢量方程,我们以后会讨论更多。您可以将这个方程压缩到我们所称的表[Ab]或我们所称的强化矩阵中。

Now we can use this and apply row reduction on the matrix to solve the system.
::现在,我们可以使用此功能,并在矩阵上进行减排,以解决系统问题。

The goal of this is to get one's down the diagonal and 0's everywhere else and then new values in terms of the d's. This is essentially just the linear equation without the variables and it's a cleaner way of applying elimination.
::这样做的目的是把一个人的对角线下下去, 0's其他任何地方, 然后新的数值在 d's 上。这基本上是没有变量的线性方程式, 并且是一种更干净的消除方法。

Having one's down the diagonal equaling to corresponding augment represents the solutions for $\begin{aligned} x_{1}, x_{2} and x_{3} \end{aligned}$ because the rows represent the equations and the columns represent the vectors of coefficients. For later terminology, the entries with ones are called pivots.
::单线下方的对角线等于相应的增量, 代表 x1, x2 和 x3 的解决方案, 因为行代表方程, 列代表系数的矢量。以后的术语是, 带边线的条目称为 pivits 。

What we do next is we apply row operations . Simplifying matrices can be done with three elementary row operations, swapping rows, scaling rows, and adding scalar multiples of one row upon another.
::接下来我们要做的是应用行操作。简化矩阵可以通过三个小行操作、换行、缩放行和增加一个行的卡路里倍数来完成。

Let's try out some examples:
::让我们举几个例子:

Example 1:
::例1:

$\begin{aligned} 3 x_{1} - 2 x_{2} + 5 x_{3} = 20 \\ - 4 x_{1} + 3 x_{2} - x_{3} = - 10 \\ 1 x_{1} - 9 x_{2} + 3 x_{3} = 19 \end{aligned}$
::3x1 - 2x2+5x3=20 - 4x1+3x2 - x3101x1 - 9x2+3x3=19

Now, turn this into a vector equation to get
::现在,把这个转换成矢量方程

$\begin{aligned} [\begin{matrix} 3 \\ - 4 \\ 1 \end{matrix}] x_{1} + [\begin{matrix} - 2 \\ 3 \\ - 9 \end{matrix}] x_{2} + [\begin{matrix} 5 \\ - 1 \\ 3 \end{matrix}] x_{3} = [\begin{matrix} 20 \\ - 10 \\ 19 \end{matrix}] \end{aligned}$
::[3-41]x1+[-23-9]x2+[5-13]x3=[20-1019]

Then we get the matrix vector product
::然后我们得到母体矢量产品

$\begin{aligned} [\begin{matrix} 3 & - 2 & 5 \\ - 4 & 3 & - 1 \\ 1 & - 9 & 3 \end{matrix}] \cdot [\begin{matrix} x_{1} \\ x_{2} \\ x_{3} \end{matrix}] = [\begin{matrix} 20 \\ - 10 \\ 19 \end{matrix}] \end{aligned}$
::[3-25-43-11-93] [x1x2x3] =[20-1019]

which gives us our augmented matrix
::这使得我们有了扩大的矩阵表

$\begin{aligned} [\begin{matrix} 3 & - 2 & 5 & 20 \\ - 4 & 3 & - 1 & - 10 \\ 1 & - 9 & 3 & 19 \end{matrix}] \end{aligned}$

You do not usually need to go through all of these steps to get the augmented matrix, but just for the sake of visualization and understanding how you get there, I included it.
::你通常不需要经过所有这些步骤才能得到扩充的矩阵, 但是为了直观化和理解你是如何到达那里, 我把它包括进去了。

Now we apply row reduction (or elimination).
::现在,我们适用减排(或取消)。

First, swap row one and row three giving us
::第一,交换一排和三排给我们

$\begin{aligned} [\begin{matrix} 1 & - 9 & 3 & 19 \\ - 4 & 3 & - 1 & - 10 \\ 3 & - 2 & 5 & 20 \end{matrix}] \end{aligned}$ .

Now let's multiply row 1 by 4 and add it to the second row, replacing that onto the second row.
::现在让我们乘以第1行第4行,把它加到第二行,将它替换到第二行。

This gives us
::这给了我们

$\begin{aligned} [\begin{matrix} 1 & - 9 & 3 & 19 \\ 0 & - 33 & 11 & 66 \\ 3 & - 2 & 5 & 20 \end{matrix}] \end{aligned}$ .

Then let's try to eliminate the 3 in the third row by multiplying the first row by negative three and then adding it to the third row then replacing the first row.
::那么让我们尝试去掉第三行的3, 将第一行乘以负三, 然后将其加到第三行, 然后替换第一行。

That gives us
::这给了我们

$\begin{aligned} [\begin{matrix} 1 & - 9 & 4 & 19 \\ 0 & - 33 & 11 & 66 \\ 0 & 25 & - 4 & 37 \end{matrix}] \end{aligned}$

Now let's try to eliminate the 25 and -9 in the second column, because again we want to get explicit formulas for $\begin{aligned} x_{1}, x_{2} and x_{3} \end{aligned}$ . First, let's eliminate 25 by multiplying the second row by 25/33 and then adding it to the third row, placing it upon the third row.
::现在让我们尝试去掉第二列中的 25和 -9, 因为再次我们要获得 x1, x2 和 x3 的清晰公式。首先, 让我们删除 25, 将第二行乘以 25/33 , 然后将其加到第三行, 将其放在第三行。

Now we have
::现在,我们

$\begin{aligned} [\begin{matrix} 1 & - 9 & 3 & 19 \\ 0 & - 33 & 11 & 66 \\ 0 & 0 & \frac{13}{3} & 13 \end{matrix}] \end{aligned}$

A quick side note, this called an echelon form. We have a triangular matrix (a matrix which has 0's all above or below the diagonal where the two types of triangular matrices are upper and lower triangular matrices). What we mean by calling this an echelon form is now that we have an explicit term for $\begin{aligned} x_{3} \end{aligned}$ we can just stop and continuously plug back in, but for the sake of completion I will not stop.
::快速的侧边注意, 这叫做梯层。我们有一个三角矩阵( 矩阵上方或下方为 0 的顶端或下方 ) 。我们所说的“ 梯层 ” , 意思是现在我们有一个明确的x3 术语, 我们可以停止并不断插入, 但是为了完成, 我将不会停止。

Now let's multiply the third row by $\begin{aligned} \frac{3}{13} \end{aligned}$ to get
::现在让我们把第三行乘以313乘以313

$\begin{aligned} [\begin{matrix} 1 & - 9 & 3 & 19 \\ 0 & - 33 & 11 & 66 \\ 0 & 0 & 1 & 3 \end{matrix}] \end{aligned}$

Now because we have a one in the third row and third column let's easily eliminate the 3 and 11 in the third column. First we multiply the third row by -11 then add it to row 2 and place that upon row 2 and then do the same for the first row except using 3 as our scalar multiple.
::现在,因为我们在第三行和第三列中有一个, 让我们很容易地去掉第三列中的第3和11。首先, 我们把第三行乘以 - 11, 然后加到第二行, 然后把第二行放在第二行上, 然后对第一行也这样做, 除了使用三作为我们的标值倍数之外。

This gets us to
::这让我们想到

$\begin{aligned} [\begin{matrix} 1 & - 9 & 0 & 10 \\ 0 & - 33 & 11 & 66 \\ 0 & 0 & 1 & 3 \end{matrix}] \end{aligned}$

and then too
::和和和和和

$\begin{aligned} [\begin{matrix} 1 & - 9 & 0 & 10 \\ 0 & - 33 & 0 & 33 \\ 0 & 0 & 1 & 3 \end{matrix}] \end{aligned}$

Next, multiply the second row by $\begin{aligned} - \frac{1}{33} \end{aligned}$ to get
::下一步, 乘以第二行乘以- 133 获得

$\begin{aligned} [\begin{matrix} 1 & - 9 & 0 & 10 \\ 0 & 1 & 0 & - 1 \\ 0 & 0 & 1 & 3 \end{matrix}] \end{aligned}$ .

Finally multiply row two by 9 and then add it onto row 1 replacing it onto row 1 to get $\begin{aligned} [\begin{matrix} 1 & 0 & 0 & 1 \\ 0 & 1 & 0 & - 1 \\ 0 & 0 & 1 & 3 \end{matrix}] \end{aligned}$
::最后将第二行乘以9乘以9,然后将其加入第一行,将其替换为第一行,以获得 [100101010-10013]

In conclusion our solution is
::最后,我们的解决办法是:

$\begin{aligned} [\begin{matrix} x_{1} \\ x_{2} \\ x_{3} \end{matrix}] = [\begin{matrix} 1 \\ - 1 \\ 3 \end{matrix}] \end{aligned}$
::[x1x2x3] = [1-13]

Now let's look at some cases that don't work out so nicely and then think to ourselves what these cases mean both algebraically and geometrically.
::现在让我们看看有些情况不太顺利然后想想这些情况在代数和几何方面都意味着什么

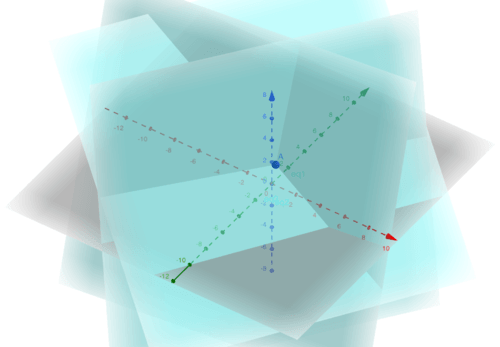
First, let's discuss the case we just had. We just had a consistent system of equations where the columns were linearly independent and spanned $\begin{aligned} R^{3} \end{aligned}$ and there existed one unique solution for the vector that was on the right hand side of the augment. One other key property was that there were the same number of direct solutions as entries (i.e., there were no zero rows) and there were as many equations as variables.
::首先,让我们来讨论一下我们刚刚遇到的情况。我们刚刚有一个一致的方程系统, 列线是线性独立的, 横跨 R3, 并且对矢量有一个独特的解决方案, 位于增强的右侧。另外一个关键属性是, 直接的方程和条目一样多( 即没有零行) , 而方程和变量一样多。

Geometrically we got a picture like
::我们的几何图画像

The first few comments about the properties are something you should ponder geometrically yourself and connect back to what we talked about earlier in span relating to solution sets.
::有关这些属性的最初几句评论是一些你应该从几何角度思考的东西,并且与我们早些时候在与成套解决方案有关的问题上所谈到的内容联系起来。

However, the last statement is imperative in the relationship between the number of variables and the number of equations.
::然而,在变量数和方程数之间的关系方面,最后一句话是绝对必要的。

First, think about it geometrically in terms of lines and planes and what not, but the number of equations must be greater than or equal to the number of variables, because if it is less we may just have two planes intersecting in a line or one line just in space.
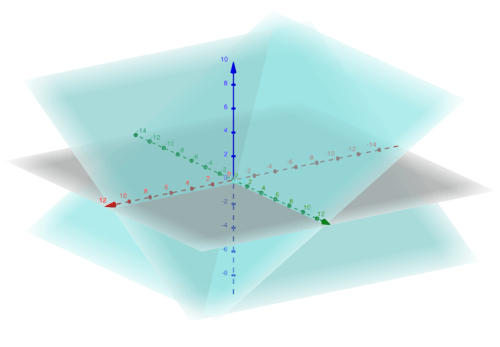
::首先,从线条和平面的几何角度来考虑它,等等,但方程的数量必须大于或等于变量的数量,因为如果数量较少,我们可能仅仅在一行或一行空间内有两平面交叉。

Next, let's think about a case we have not seen an example of yet. Sometimes our augmented matrix may have a row of 0s. This still means that the system is consistent also that the columns may be linearly dependent . For example, take the augmented matrix of the form $\begin{aligned} [\begin{matrix} a_{1} & 0 & a_{2} & a_{3} \\ 0 & b_{1} & b_{2} & b_{3} \\ 0 & 0 & 0 & 0 \end{matrix}] \end{aligned}$

which would give us only solutions for $\begin{aligned} x_{1} and x_{2} \end{aligned}$ in terms of $\begin{aligned} x_{3} \end{aligned}$ making $\begin{aligned} x_{3} \end{aligned}$ a free variable. When you get a matrix like this it is most likely because there are more variables than equations.

Though the row of 0's may be a consequence of row reduction this still represents a system where a bunch of planes intersect at a line giving infinitely many solutions so you should think about how this relates to linear dependence and span.

Again, a plane related picture may look like

Our last case is where there is no solution. This happens when you get a matrix with one row of zeros with a nonzero augment which represents the equation 0 equals something nonzero which is false showing there are no solutions. This also represents that the vector you are looking for is not in the span of the column vectors. This sometimes can happen if there are more variables than equations, but try to think about the case where the number of variables equals the number of equations and how that relates to linear dependence and independence.
::我们的最后一个案例是不存在解决方案的地方。发生这种情况的条件是, 您得到一个矩阵, 带有一行零, 非零增量, 代表方程式 0 等于非零, 虚假显示没有解决方案。这还表明您所要寻找的矢量不在列矢量的范围之内。有时如果变量多于方程式, 则可能发生这种情况, 但是要考虑变量数量等于方程式数量, 以及它如何与线性依赖性和独立性相关的情况。

In terms of planes you may either get two parallel planes and a third arbitrary plane, three planes where each plane is parallel to the line representing intersection of the other two or just three parallel planes.

Review problems

Solve, analyze and draw geometrically

$\begin{aligned} 3 x_{1} + 4 x_{2} - 5 x_{3} = 1 \\ - 3 x_{1} - 4 x_{2} - 5 x_{3} = 19 \\ - x_{1} - \frac{4}{3} x_{2} + \frac{5}{3} x_{3} = - \frac{4}{3} \end{aligned}$
::3x1+4x2-5x3=1-3x1-4x2-5x3=19-x1-43x2+53x3**43

::解密、分析和绘制 3x1+4x2-5x3=1-3x1-4x2-5x2-5x3=19-x1-43x2+53x3=43

Solve for $\begin{aligned} x_{1}, x_{2}, x_{3} and x_{4} \end{aligned}$

$\begin{aligned} [\begin{matrix} 3 \\ 2 \\ - 1 \\ 4 \end{matrix}] x_{1} + [\begin{matrix} 4 \\ 3 \\ 1 \\ 5 \end{matrix}] x_{2} + [\begin{matrix} - 2 \\ 1 \\ - 3 \\ 7 \end{matrix}] x_{3} + [\begin{matrix} - 1 \\ 2 \\ - 4 \\ 6 \end{matrix}] x_{4} = [\begin{matrix} - 2 \\ 5 \\ - 18 \\ 25 \end{matrix}] \end{aligned}$
::[32-14]x1+[4315]x2+[-21-37]x3+[-12-46]x4=[-25-1825]

::x1, x2, x3 和 x4 [32- 14] x1+[4315] x2+[- 21- 37]x3+[- 12-46]x4=[- 25- 1825]

Solve this augmented matrix $\begin{aligned} [\begin{matrix} - 2 & - 1 & 4 & - 1 \\ 1 & 5 & 1 & 3 \\ 0 & - 3 & 2 & 2 \end{matrix}] \end{aligned}$
::解决这一扩大的矩阵[-2-14-115-1130-322]

Solve for $\begin{aligned} x_{1}, x_{2} and x_{3} \end{aligned}$

$\begin{aligned} 3 x_{1} + 4 x_{2} - 3 x_{3} = 2 \\ - 2 x_{1} + 5 x_{2} - 2 x_{3} = 6 \\ 3 x_{1} + 4 x_{2} - 3 x_{3} = 3 \end{aligned}$
::3x1+4x2-3x3=2-2x1+5x2-2x3=63x1+4x2-3x3=3

::x1, x2和 x3 3x1+4x2-3x3=2-2x1+5x2-2x3=63x1+4x2-3x3=3

章节大纲

常规

缩排