Course: 1.8 理性模型介绍-interactive | The Way To Learn

The Way To Learn

Section outline

Select section General

Collapse Expand
General

Collapse all Expand all
- Select activity 新闻通告
  
  新闻通告 Forum
Select section 引入理性模型

Collapse Expand
引入理性模型
The Purpose of T his Lesson
::本课程的目的

In this lesson, you will use a rational function to model density as a function of volume . You will compare and contrast this model with linear, exponential, and quadratic functions.
::在此课中, 您将使用一个理性函数来模拟密度作为音量函数。您将用线性、指数性和二次函数来比较和对比这个模型。

Introduction: Density, Mass, and Volume
::导言:密度、质量和数量

Density is a measure of the concentration of mass within a space. There are multiple different units for measuring density, but in this lesson, you use kilograms per cubic meter.
::密度是测量空间内质量浓度的尺度。测量密度有多种不同的单位,但在此课中,您使用每立方米公斤。

Density
::密度

Density is the mass of an object divided by its volume.
::密度是指物体的重量除以其体积。

The equation for density is $\begin{aligned} D = \frac{m}{V} \end{aligned}$ .
::密度方程式是 D=mV。

A common unit of density measure is kilograms per cubic meter.
::共同密度单位为每立方米公斤。

Activity 1: Calculating Density
::活动1:计算密度

Example 1-1
::例1-1

1000 liters is equivalent to 1 cubic meter. A cubic meter is about the amount of space taken up by a washer and dryer.
::1 000升等于1立方米,1立方米等于洗衣机和烘干机占用面积。

A washer and dryer take up about 1 cubic meter of space

Visualize a 1-liter bottle of water. One liter of water has a mass of 1 kilogram. A kilogram is about 2.2 pounds.
::一升水质量为1公斤,一公斤约为2.2磅。

One liter of water has a mass of one kilogram. One kilogram is about 2.2 pounds.

D ensity is mass divided by volume. What is the density of water, in kilograms per cubic meter? What's the mass of a cubic meter of water?
::密度是质量除以体积。水的密度是多少,每立方米公斤?每立方米水的密度是多少?

Solution: There are 1000 liters in a cubic meter. The fact that a liter of water has a mass of 1 kilogram makes the calculation simple:
::溶液:每立方米有1000升。一升水质量为1公斤这一事实使得计算简单:

$\begin{aligned} \begin{array}{l} D_{water} = \frac{1000 kg}{1 m^{3}} \\ D_{water} = 1000 kg / m^{3} \end{array} \end{aligned}$

The mass of a cubic meter of water is 1000 kilograms. That's about 2200 pounds. That's pretty close to the mass of a Fiat 500.
::Dwater=1000公斤1立方米Dwater=1000公斤/立方米1 000公斤立方米水质量为1000公斤。大约2200磅。这几乎接近Fiat 500的重量。

A cubic meter of water is 1000 kilograms, about the mass of a very small car.

PLIX Interactive
::PLIX 交互式互动

Example 1-2
::例1-2

Match each of the following materials with its correct density. (They are currently not matched correctly.) Order them from least to greatest density. Make observations about the relative densities of these materials.
::将以下每种材料与准确密度匹配。 (目前没有正确匹配。) 命令它们从最小密度到最大密度。观察这些材料的相对密度。

$\begin{aligned} \begin{array}{ll} Material & Density (kg / m^{3}) \\ Styrofoam & 225 \\ Fresh Water & 50 \\ Cork & 750 \\ Salt Water & 917 \\ Balsa Wood & 1000 \\ Steel & < 1 molecule / m^{3} \\ Helium (at sea level) & 130 \\ Outer Space & 0.2 \\ Ice & 8050 \\ Oak & 1027 \end{array} \end{aligned}$
:kg/m3) 材料密度(千克/立方米) 烟气泡沫225Fresh Water50Cork750Salt Water917Balsa Wood1000Steel <1分子/立方米Hium(海平面)130

Solution:

$\begin{aligned} \begin{array}{ll} Material & Density (kg / m^{3}) \\ Outer Space & < 1 molecule / m^{3} \\ Helium (at sea level) & 0.2 \\ Styrofoam & 50 \\ Balsa Wood & 130 \\ Cork & 225 \\ Oak & 750 \\ Ice & 917 \\ Fresh Water & 1000 \\ Salt Water & 1027 \\ Steel & 8050 \end{array} \end{aligned}$
::溶液: 物质密度(kg/m3) 外层空间 < 1分子/立方米 (海平面)0.2Styrofoam50Balsa Wood130Cork225Oak750Ice917Fresh Water1000Salt Water1027Steel8050

Some observations:
::一些意见:

A cubic meter of Helium still has a mass of 0.2 kilograms - about equivalent to a container of lunch milk.
::氢的立方厘米仍然有0.2公斤的质量,大约相当于一个午餐牛奶容器。

A cubic meter of styrofoam would be pretty hard to lift - not just because it would take up a space equivalent to about a washer and dryer. 50 kilograms is about 110 pounds.
::一立方米的气泡泡沫将很难提升 - 不仅仅是因为它会占用一个空间相当于一个洗衣机和烘干机。 50公斤大约110磅。

Balsa wood is less dense than cork.
::Balsa木质比软木密度低。

Ice is less dense than fresh water, but not by much.
::冰的密度比淡水低,但不多。

Freshwater is less dense than salt water. (So, is it "easier" to float in fresh or salt water? Why?)
::淡水的密度比盐水低。 (那么,在淡水或盐水中漂浮是“容易? ”为什么? )

Steel is about 8 times as dense as water.
::钢铁的密度是水的8倍

Activity 2: Rational Functions
::活动2:合理函数

Example 2-1
::例2-1

Denver is about a mile above sea level. The density of air in Denver is about 1 kilogram per cubic meter. I magine taking 1 kilogram of air in Denver and distributing it throughout a container with a volume of 2 cubic meters. What's the density of that air now? What if you compress 1 kilogram of air into a half of a cubic meter? What's the density now? Create a table that shows the relationship between volume and density. Create an equation for density as a function of volume. Is this equation of a type with which you are familiar, or is it a new type? What name would you give this function? Graph the function, adding data to your table as needed. What are some characteristics of this function? Interpret these characteristics in the context of the density scenario.
::丹佛的空气密度大约是海平面的一英里。丹佛的空气密度大约是每立方米1公斤。想象一下在丹佛取1公斤的空气, 并在2立方米的容器中分布。现在空气的密度是什么? 如果将1公斤的空气压缩成半立方米的密度是什么? 现在的密度是什么? 创建一个显示体积和密度之间关系的表格。创建密度的方程式作为体积的函数。这个方程式是您熟悉的类型, 还是一个新类型? 您给这个方程式取什么名字? 描述这个函数, 按需要将数据添加到表格中。这个函数的一些特性是什么? 在密度假设中解释这些特性。

Solution: The density of 1 kilogram of air in 2 cubic meters of space is calculated as:

$\begin{aligned} \begin{array}{l} D = \frac{m}{V} \\ D = \frac{1}{2} \\ D = 0.5 kg / m^{3} \end{array} \end{aligned}$

::溶解度:2立方米空间1千克空气密度计算为:D=mVD=12D=0.5千克/立方米

The density of 1 kilogram of air in a half of a cubic meter is calculated as:
::半立方米内1公斤空气的密度计算如下:

$\begin{aligned} \begin{array}{l} D = \frac{1}{0.5} \\ D = 2 kg / m^{3} \end{array} \end{aligned}$

::D=10.5D=2千克/立方米

In general, density as a function of volume in this scenario is given by the equation:

$\begin{aligned} D = \frac{1}{V} \end{aligned}$

::一般说来,密度作为本假设情景中量函数的密度是由公式D=1V给出的:D=1V

$\begin{aligned} \begin{array}{ll} Volume (m^{3}) & Density kg / m^{3} \\ 0.1 & 10 \\ 0.2 & 5 \\ 0.5 & 2 \\ 1 & 1 \\ 2 & 0.5 \\ 10 & 0.1 \\ 20 & 0.05 \end{array} \end{aligned}$

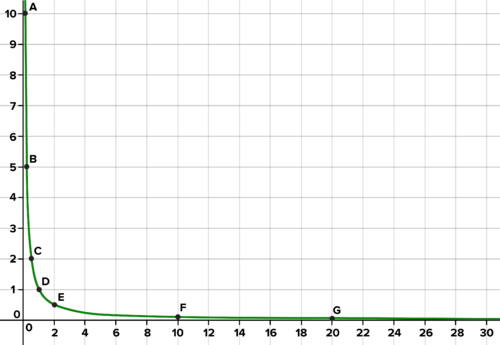
::体积(m3) 密度千克/m30.1100.250.5211120.50100.1200.05

This is not linear, not exponential, and not quadratic. Because this function is a ratio with a variable in the denominator, this is called a rational function .
::这不是线性,不是指数性,也不是二次曲线。由于此函数是分母中变量的比,所以这被称为理性函数。

As volume increases on the x-axis, density, on the y-axis, decreases

The graph illustrates that as volume increases, the density decreases. It also shows that as the volume decreases, the density increases.
::该图显示,随着量的增加,密度会减少,还显示,随着量的减少,密度会增加。

When the volume is very small, the density is very large. For example, a volume of 0.1 cubic meters results in a density of 10 kilograms per cubic meter. Volume does not go below zero.
::当体积非常小时,密度非常大。例如,0.1立方米的体积导致每立方米密度为10公斤。体积不低于零。

When the volume is very large, the density is very small. For example, a volume of 20 cubic meters yields a density of 0.05 kilograms per cubic meter. Density never goes below zero.
::当体积非常大时,密度非常小。例如,20立方米的体积每立方米的密度为0.05公斤。密度从不低于零。

Rational Functions
::理性函数

Simple rational functions have the form of $\begin{aligned} y = \frac{a}{x} \end{aligned}$ , where $\begin{aligned} a \end{aligned}$ is a constant .
::简单理性函数具有y=ax的形式,其中一个函数为常数。

The function for density as a function of volume is $\begin{aligned} D = \frac{m}{V} \end{aligned}$ .
::密度作为音量函数的函数为 D=mV。

Density decreases as volume increases.
::密度随着量的增加而减少。

Density increases as volume decreases.
::密度随着数量减少而增加。

Neither density nor volume can reach a value of 0.
::密度和体积均不能达到0值。

The relationship between density and volume is an example of inverse variation. Quantities are inversely proportional if as one quantity increases, the other decreases . In general, inverse variation can be modeled using the function $\begin{aligned} f (x) = \frac{k}{x}, \end{aligned}$ where $\begin{aligned} k \end{aligned}$ is the constant of variation and must be a nonzero number.
::密度和体积之间的关系是反向变化的一个例子。如果以一个数量增加,另一个数量减少,数量是反比的。一般来说,反比可以使用函数f(x)=kx来模拟,K是变量的常数,必须是非零数。

Example 2-2
::例2-2

The law of the fulcrum states the distance from the fulcrum varies inversely as the weight of the object. Joey and Josh are on a seesaw. If Joey weighs 40 pounds and sits six feet from the fulcrum, how far from the fulcrum would Josh (who weighs 65 pounds) have to sit to balance the seesaw?
::支架法则指出与支架的距离与物体的重量不同。Joey和Josh在锯木上。如果Joey重40磅,坐在距支架6英尺的地方,Josh(65磅)要坐多远才能平衡支架?

Solution: We know that functions of inverse variation look like $\begin{aligned} f (x) = \frac{k}{x}, \end{aligned}$ so we can substitute in known values to solve for $\begin{aligned} k . \end{aligned}$
::解答: 我们知道反变量的函数看起来像 f( x) =kx, 所以我们可以用已知的数值替代 k。

$\begin{aligned} distance & = \frac{k}{weight} \\ 6 & = \frac{k}{40} \\ k & = 240 \end{aligned}$

::距离=k重量6=k40k=240

Then we use the function to find the distance Josh would have to sit to balance the seesaw.
::然后我们用这个功能找到Josh必须坐的位置来平衡木锯的距离

$\begin{aligned} distance & = \frac{240}{weight} \\ distance & = \frac{240}{65} \approx 3.7 feet \end{aligned}$

::距离=240体重距离=240653.7英尺

Inverse Variation
::反反变化

Simple rational functions are described as inverse variations because increasing one variable decreases the other variable by the same multiple.
::简单理性函数被描述为反向变化,因为增加一个变量使另一个变量减少同一个倍数。

The form of inverse variation, $\begin{aligned} y = \frac{k}{x}, \end{aligned}$ is the same as the form of simple rational functions, $\begin{aligned} y = \frac{a}{x}, \end{aligned}$ where $\begin{aligned} a \end{aligned}$ or $\begin{aligned} k \end{aligned}$ must be a nonzero constant.
::y=kx 的反向变化形式与 y=ax 的简单理性函数形式相同, y=ax 必须是非零常数的或 k 。

Activity 3: Modeling with Rational Functions
::活动3:利用合理功能建模

Interactive
::交互式互动

Below is an interactive graph of the rational function you graphed above. In the interactive, you can change $\begin{aligned} m \end{aligned}$ to see how the graph of density changes. Observe the results and record your observations. As you change the mass, does the graph retain some of its characteristics? Why?
::下面是您在上面绘制的理性函数的交互式图形。在互动中,您可以修改 m 以查看密度图形是如何变化的。观察结果并记录您的观测结果。当您改变质量时,该图形是否保留了其某些特性?为什么?

INTERACTIVE

Simple Rational Model

Move the red point to change the value of the constant, $m.$
::移动红色点以更改值, m.

The horizontal axis represents volume $(V)$ and the vertical axis represents density $(D).$
::水平轴代表体积(V),垂直轴代表密度(D)。

Observe how the graph changes as the value of $m$ varies.
::观察图形如何改变 m 值。

Your device seems to be offline.
Please check your internet connection and try again.

+

Do you want to reset the PLIX?

Yes

No

Work It Out
::F. 工作外外

Use the equation for the density of a kilogram of air from above to determine the density of 1 kilogram of air in a container with a volume of 100 cubic meters.
::使用一公斤以上空气密度的方程来确定一个容量为100立方米的容器中的1公斤空气密度。

Write and solve an equation to determine what volume of container would be required to give 1 kilogram of air a density of 100 kilograms per cubic meter. Use the guide below to help you solve this sort of equation.
::写入并解析一个方程, 以确定给1公斤空气以每立方米100公斤密度需要多少量的容器。使用下面的指南帮助您解析这种方程。

Solving a Rational Equation (Example)
::解决合理等式(示例)

$\begin{aligned} \begin{array}{ll} 5 = \frac{7}{x} & Given equation \\ 5 x = 7 & Multiply both sides by x \\ x = \frac{7}{5} & Divide both sides by 5 \end{array} \end{aligned}$

Write and solve an equation to determine what volume of container would be required to give 1 kilogram of air a density equivalent to that of Balsa Wood. What volume of container would be required to give 1 kilogram of air a density equivalent to that of fresh water?
::编写和解决一个方程,以确定给1公斤空气以相当于Balsa Wood的密度需要多少集装箱,给1公斤空气以相当于淡水的密度需要多少集装箱?

Suppose there is a series of air chambers as shown below. Create a table which shows the relationship between the side length in meters of the square base and the volume of the resulting figure. Extend your table beyond the three containers shown, following the observed pattern . Write an equation for volume as a function of the side length. Graph the resulting function. What kind of function is this? Describe its characteristics.
::假设下面有一系列的空舱。创建一个表格, 显示以平方米计的边长与所生成的图量之间的关系。将您的表格扩展到所显示的三个容器之外, 按照观察到的模式。将体积的方程式写成以侧长度函数为单位的方程式。绘制由此得出的函数。这是哪种函数? 描述其特性。

3 containers, each with 10 kg of air inside. Each unit on the graph is 1 meter.

Suppose there are 10 kilograms of air in each of these containers. Given that each unit on the graph is 1 meter, c omplete the table below showing the relationship between side length, volume, and density of 10 kilograms of air in each container. Write an equation for the density as a function of side length .

$\begin{aligned} \begin{array}{cll} Side length & Volume & Density \\ 1 \\ 2 \\ 3 \\ 4 \\ 5 \\ 6 \\ x \end{array} \end{aligned}$

::假设每个容器都有10公斤的空气。鉴于图表上每个单元为1米,请填写下表,显示每个容器内10公斤空气的长度、体积和密度之间的关系。写一个密度的方程式作为侧长的函数。侧长度123456x

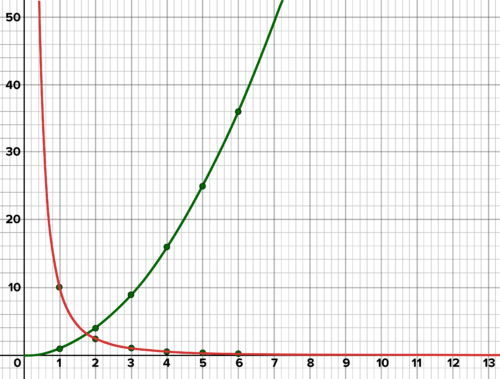
Below is a graph showing both the volume as a function of side length and the density as a function of side length. That means the $\begin{aligned} y \end{aligned}$ -axis is representing two different units at the same time. What are the two units, and for which graphs does each unit apply? What does the $\begin{aligned} x \end{aligned}$ -axis represent? Describe the graph of volume as a function of side length, and the graph of density as a function of side length. Describe the relationship between the two graphs. Explain why these relationships exist.
::下面是一个图表,显示音量是侧长的函数,密度是侧长的函数。这意味着 Y - 轴同时代表两个不同的单位。两个单位是哪个单位, 每个单位适用哪些图形? x 轴代表什么? 将音量图描述为侧长的函数,而密度图则表示为侧长的函数。描述两个图表之间的关系。解释这些关系存在的原因。

Volume and density, each as a function of side length.

(extension) Is there a point where the two graphs cross? Write and solve an equation to determine the $\begin{aligned} x \end{aligned}$ -coordinate of this point. Then use that value to determine the $\begin{aligned} y \end{aligned}$ -coordinate.
:扩展) 是否有两个图形交叉的点 ? 写入并解析一个方程式以确定此点的 x 坐标。然后使用该值来确定 Y 坐标。

(extension) For the rational function $\begin{aligned} y = \frac{30}{x} \end{aligned}$ , are there any values that cannot be substituted for $\begin{aligned} x \end{aligned}$ ? Why or why not?
::对于 y= 30x 的理性函数, 是否有任何值不能替换 x 。为什么或为什么 ?

Compare and contrast linear, exponential, quadratic, and rational functions based on their equations and graphs. Discuss how the values returned by each change as $\begin{aligned} x \end{aligned}$ changes.
::比较和对比线性、指数性、二次曲线和基于方程式和图形的理性函数。讨论每个变化返回的数值是如何随着 x 变化而变化的。

Remember This
::记住这个

Simple rational functions have the form $\begin{aligned} y = \frac{a}{x} \end{aligned}$ , where $\begin{aligned} a \end{aligned}$ is a constant.
::简单理性函数具有y=ax的窗体,其中一个函数为常数。

In a rational function, as $\begin{aligned} x \end{aligned}$ increases, $\begin{aligned} y \end{aligned}$ decreases, without ever reaching 0.
::在一个理性函数中,随着 x 的增加,y 减少, 从未达到 0。

In a rational function, as $\begin{aligned} x \end{aligned}$ gets small without reaching 0, $\begin{aligned} y \end{aligned}$ gets large.
::在合理函数中, 当 x 变小时没有达到 0, y 会变大。

PLIX Interactive
::PLIX 交互式互动

版权所有 © 2024 由瓜瓜科技thewaytolearn.cn设计。保留所有权利。