3.10 赤道模型-interactive

Section outline

• Select section General

  Collapse Expand

  General

  Collapse all Expand all

  • Select activity 新闻通告

    

    新闻通告 Forum
• Select section 二次曲线模型

  Collapse Expand

  二次曲线模型

  播放段落

  The Purpose of this Lesson
  ::本课程的目的

  播放段落

  In this lesson, you will develop a quadratic model by adding linear and constant terms .
  ::在此教训中,您将开发一个二次模型, 添加线性和恒定的术语 。

  ---

  播放段落

  Activity 1:  Objects Undergoing Constant Acceleration
  ::活动1:不断加速的物体

  

  播放段落

  Work it Out
  ::工作出来

  播放段落
  1. Greg  pilots a   speed boat on a lake, and  is accelerating at 3 meters per second, per second. Recall that if an object is undergoing constant acceleration, the distance it has traveled as a function of time is given by  $\begin{array}{r}y=\frac{1}{2}a{x}^2,\end{array}$  where  $\begin{array}{r}a\end{array}$  is acceleration. Create an equation for the distance the boat has traveled as a function of time. How far has Greg's  boat traveled in 10 seconds? When does the boat pass the 1-kilometer mark?
     ::格雷格在湖上驾驶一艘快艇, 加速速度为每秒3米, 每秒3米。 提醒注意如果一个物体正在不断加速, 它作为时间函数所走的距离由 y= 12ax2 给出, 加速度由 y= 12ax2 给出, 加速度由 y= 12ax2 给出 。 为该船作为时间函数所走的距离创建方程式。 格雷格的船在10 秒内行驶到什么程度? 当该船通过 1 公里标记时 ?
  播放段落
  2. Greg races against a recreational  boat piloted by his friend Gillian. Gillian travels at a constant 8 meters per second. In order to make the race somewhat fair, Greg gives Gillian an 80-meter head start. Create an equation for the distance that Gillian's boat has traveled as a function of time (including the head start). Sketch a graph of both. Determine how far each has traveled by the 5-second mark. Write, but do not solve, an equation to determine when one passes the other. Use solving or graphing technology to determine the solution. How far has each traveled by this time?
     ::Greg和他的朋友Gillian驾驶的游艇赛跑。Gillian每秒以8米恒定的距离旅行。为了让比赛变得公平一些,Greg给Gillian一个80米长的起点。为Gillian的船在时间上行驶的距离(包括开船头)建立一个方程式。绘制一个两者的图。确定每个人在5秒的标记上行走多远。写一个方程,但不能解开,以决定一个人通过对方的时间。使用解析或图形化技术来决定解决办法。每个方程在这个时候走多远?
  播放段落
  3. Greg's friend Monica also has a speedboat. Greg and Monica decide to race. Greg's boat accelerates at 3 meters per second, per second as before. Monica's boat accelerates at 5 meters per second, per second. Monica gives Greg a 200-meter head start. Create functions that model the distance each has traveled as a function of time. Graph. Write and solve equations to determine when each passes the 2-kilometer mark. Write and solve an equation to determine when one passes the other.
     ::Greg的朋友Monica也有一艘快艇。Greg和Monica决定比赛。Greg的船加速速度为每秒3米,每秒每秒3米。Monica的船加速速度为每秒5米。Monica给Greg一个200米的起始点。创建函数来模拟每个行走的距离作为时间的函数。图。写和解析方程式以确定每个行走的方程式何时经过2公里的标记。写和解析一个方程式以确定一个行走的方程式何时经过另一个。

  播放段落

  Interactive
  ::交互式互动

  播放段落

  In the interactive below, explore changing the parameters for Greg and Gillian's race . Move the red point to change the acceleration for Greg's boat and move the blue point to change how much of a head start Gillian's boat has. Both functions are graphed such that one boat passes the other at the 15-second mark. Click the "Evaluate" button to see how far the boats are when one passes the other.  
  ::在下文的互动中, 探索改变 Greg 和 Gillian 的赛跑参数。 移动红点以改变 Greg 的船加速度, 移动蓝点以改变 Gillian 的船头起动的速率。 两种功能都有图表显示, 一艘船在 15 秒的 标记处经过另一艘船。 单击“ Evaluate ” 按钮可以看一艘船只经过另一艘船的距离 。

  

  INTERACTIVE

  Intersection of Linear and Quadratic Functions

  

  播放段落
  • Move the red point to change the acceleration for Greg's boat and move the blue point to change how much of a head start Gillian's boat has. 
    ::移动红点以改变Greg的船加速度 移动蓝色点以改变Gillian的船头起动量
  播放段落
  • Click the "Evaluate" button to see how far the boats are when one passes the other.  
    ::单击“ Evaluate” 按钮以查看在一条船经过另一条船时船只有多远 。

  Your device seems to be offline.
  Please check your internet connection and try again.

  ---

  +

  Do you want to reset the PLIX?

  Yes

  No

  播放段落

  Interactive
  ::交互式互动

  播放段落

  In the interactive below , explore changing the parameters for Greg and Monica's race . Move the red point to change the acceleration for Monica's boat and move the blue point to change how much of a head start Greg's boat has. Both functions are graphed such that one boat passes the other at the 9-second mark. Click the "Evaluate" button to see how far the boats are when one passes the other.  
  ::在下文的互动中, 探索改变格雷戈和莫妮卡的赛事参数。 移动红点以改变莫妮卡的船加速度, 移动蓝点以改变格雷戈的船头起动的船有多少。 两种功能都用图表显示, 一艘船在9秒的关口经过另一艘船。 单击“ 估价” 按钮可以看一艘船经过另一艘船有多远 。

  

  INTERACTIVE

  Intersection of Quadratic Functions

  

  播放段落
  • Move the red point to change the acceleration for Monica's boat and move the blue point to change how much of a head start Greg's boat has. 
    ::移动红点以改变Monica的船加速度 移动蓝色点以改变Greg的船头起动量
  播放段落
  • Click the "Evaluate" button to see how far the boats are when one passes the other.  
    ::单击“ Evaluate” 按钮以查看在一条船经过另一条船时船只有多远 。

  Your device seems to be offline.
  Please check your internet connection and try again.

  ---

  +

  Do you want to reset the PLIX?

  Yes

  No

  ---

  播放段落

  Activity 2:  Quadratics With Linear and Constant Terms
  ::活动2:有线性和常数术语的四方

  播放段落

  Example 2-1
  ::例2-1

  播放段落

  Greg decides to take his speed boat to the river. The river flows at 4 meters per second. He puts his speedboat in the river at the same time as Monica,  200 meters ahead of her. If neither turns on their motors, will Greg ever pass Monica? Why or why not?
  ::Greg决定乘他的快艇到河边,河水以每秒4米的速度流过。他把快艇和Monica放在河里,比她早200米。如果格雷格不开他们的马达,Greg会不会通过Monica?为什么或为什么不能?

  播放段落

  B oth Greg and Monica turn on their motors immediately upon putting their boats in the river. Monica  accelerates at 3 meters per second, per second, and Greg  at 2 meters per second, per second. Create functions that model the distance each has traveled as a function of time. Graph each. Write and solve an equation to determine when one passes the other. 
  ::Greg和Monica在把船放入河中时立即打开发动机。Monica加速速度为每秒3米,每秒2米,Greg加速速度为每秒2米。创建函数来模拟每个行走距离的时间函数。每个图。撰写和解析一个方程式以确定一个行走时间。

  播放段落

  Solution:   Let's start with the quadratic term for each:
  ::解答:让我们从每个词的二次词开始:

  播放段落

  $$\begin{array}{r}\begin{array}{l}M=1.5x^2\\ G=x^2\end{array}\end{array}$$

  
  ::M=1.5x2G=x2

  播放段落

  Both gain additional distance from the fact that they are in a river that's flowing at 4 meters per second. So you add this linear term:
  ::两者在一条每秒4米的河流中 都增加了距离。所以你加上这个线性词:

  播放段落

  $$\begin{array}{r}\begin{array}{l}M=1.5x^2+4x\\ G=x^2+4x\end{array}\end{array}$$

  
  ::M=1.5x2+4xG=x2+4x

  播放段落

  Finally, recall that Greg got a 200 meter head start:
  ::记得格雷格领先200米:

  播放段落

  $$\begin{array}{r}\begin{array}{l}M=1.5x^2+4x\\ G=x^2+4x+200\end{array}\end{array}$$

  
  ::M=1.5x2+4xG=x2+4x+200

  播放段落

  Here's the graph:
  ::以下是图表:

  

  播放段落

  Interactive
  ::交互式互动

  播放段落

  In the interactive below, explore changing the parameters for both models in the last problem. Move the red point to change the acceleration for Monica's boat, and move the blue point to change how much of a head start Greg's boat has, and move the green point to change the speed at which the river is flowing. Both functions are graphed such that one boat passes the other at the 9-second mark. Click the "Evaluate" button to see how far the boats are when one passes the other.
  ::在下文的互动中, 探索在最后一个问题中改变两个模型的参数。 移动红点以改变Monica的船加速度, 移动蓝色点以改变Greg的船头起动速度的多少, 移动绿色点以改变河水流的速度。 两种功能都用图表绘制, 使一艘船在9秒的标记处经过另一艘船。 单击“ 估价” 按钮以查看一艘船经过另一艘船的距离 。

  

  INTERACTIVE

  Passing Boats in a River

  

  播放段落
  • Move the red point to change the acceleration for Monica's boat.
    ::移动红点 改变莫妮卡船的加速度
  播放段落
  • Move the blue point to change how much of a head start Greg's boat has.
    ::移动蓝色点来改变Greg的船头有多少
  播放段落
  • Move the green point to change the speed at which the river is flowing. 
    ::移动绿点以改变河水流的速度。
  播放段落
  • Click the "Evaluate" button to see how far the boats are when one passes the other.
    ::单击“ Evaluate” 按钮以查看在一条船经过另一条船时船只有多远 。

  Your device seems to be offline.
  Please check your internet connection and try again.

  ---

  +

  Do you want to reset the PLIX?

  Yes

  No

  播放段落

     Quadratic Functions
  ::二次曲线函数

  播放段落

  Quadratic Functions can consist of 1,2, or 3 terms.
  ::二次曲线函数可包括1,2或3个术语。

  播放段落

  Standard form for a quadratic function is  $\begin{array}{r}y=a{x}^2+bx+c.\end{array}$
  ::二次函数的标准窗体是 y= ax2+bx+c。

  播放段落

  The first term is the quadratic term, the second the linear term, and the third the constant term. 
  ::第一个词是二次词,第二个词是线性词,第三个词是常设词。

  播放段落

  The only term that's required in order to determine a quadratic is the quadratic term.
  ::确定二次方体的唯一必要术语是二次方体术语。

  播放段落

  Work it Out
  ::工作出来

  播放段落
  1. Describe the types and characteristics  of the equations for all the functions encountered so far in this lesson.
     ::描述此课中迄今遇到的所有函数的方程式类型和特性。
  播放段落
  2. Identify the types of functions below. For those that are quadratic, state if they have a linear term, a constant term, both, or neither. For those quadratics that do not have a linear term, state the domain and range for the function. If needed, create a graph to support your statement of the range.
     ::指定下面的函数类型。 对于二次函数, 请说明它们是否有线性术语、 常数术语, 两者或两者都不是。 对于没有线性术语的二次函数, 请说明函数的域和范围。 如果需要, 请创建一个图表来支持您对范围的语句 。

  播放段落

  $\begin{array}{r}\begin{array}{ll}\text{a.}& y=x^2\\ \text{b.}& y=x^2+2x\\ \text{c.}& y=x^2+2x+3\\ \text{d.}& y=3(4{)}^x\\ \text{e.}& y=3(4{)}^x+2x\\ \text{f.}& y=\sqrt{x}\\ \text{g.}& y=\sqrt{x}+x^2\\ \text{h.}& y=5x^2+45\\ \text{i.}& y=-5x^2-45\\ \text{j.}& y=-3x^2\\ \text{k.}& y=-x^2+100\\ \text{l.}& y=\frac{5}{x}\\ \text{m.}& y=x\end{array}\end{array}$
  ::ay=x2b.y=x2+2xc.y=x2+2xx3d.y=3(4)x2x3(4)x2xf.y=xg.y=x+x2h.y=5x2+45i.y=5x2+45i.y=5x2x2-45j.y=3x2k.yx2+100l.y=5xm.y=xxxxxxx=xxxxxxxxxxxxxxxxxxxxx2-45i.y=x

  ---

  播放段落

  Activity 3:  Modeling  Acceleration Due T o  Gravity
  ::活动3:建模加速至重力

  播放段落

  Example 3-1
  ::例3-1

  播放段落

  A rock is dropped from a height of 1 kilometer. (Note: Don't do that, it's dangerous to drop rocks from cliffs!)  Neglecting air resistance, its  acceleration due to gravity is approximately 10 meters per second, per second. Create a model for the height of the rock as a function of time. Determine how high the rock is at 3 seconds. Determine when the rock has fallen half the way to the ground . Determine when the rock hits the ground. Graph.
  ::岩石从1公里高处坠落。 (注意: 不要这样做, 从悬崖上扔石头很危险 !) 忽略空气阻力, 其因重力而加速的速率约为每秒10米。 创建岩石高度的模型, 由时间函数决定。 确定岩石高度为3秒。 确定岩石跌落到地面的一半时间 。 确定岩石撞击地面的时间 。 图形 。

  播放段落

  Solution:  To model the distance of the rock from the ground, the distance the rock falls is subtracted from the given height. The equation for the height of the rock as a function of time is given by the equation (based on a formula you may have seen in Physics,  $\begin{array}{r}h=\frac{1}{2}g{t}^2):\end{array}$
  ::解答: 要建模岩石与地面的距离, 岩石坠落的距离会从给定高度中减去。 方程式给出了岩石高度作为时间函数的方程式( 根据物理中可能看到的公式, h=12gt2) :

  播放段落

  $$\begin{array}{r}y=-5x^2+1000\end{array}$$

  
  ::y5x2+1000 y5x2+1000

  播放段落

   At 3 seconds:
  ::3秒后:

  播放段落

  $$\begin{array}{r}\begin{array}{l}y=-5(3{)}^2+1000\\ y=-45+1000\\ y=955\text{meters}\end{array}\end{array}$$

  
  ::y5(3)2+1000y45+1000y=955米

  播放段落

   At the halfway mark, the height is 500 meters:
  ::在中间点,高度500米:

  播放段落

  $$\begin{array}{r}\begin{array}{l}500=-5x^2+1000\\ 5x^2=500\\ x^2=100\\ x=\pm 10\\ x=10\text{seconds}\end{array}\end{array}$$

  
  ::5005x2+10005x2=500x2=100x%10x=10秒

  播放段落

   When the rock hits the ground, the height is 0:
  ::当岩石落地时,高度是0:

  播放段落

  $$\begin{array}{r}\begin{array}{l}0=-5x^2+1000\\ x^2=200\\ x=\pm 10\sqrt{2}\\ x=10\sqrt{2}\text{seconds}\\ x\approx 14.1\text{seconds}\end{array}\end{array}$$

  
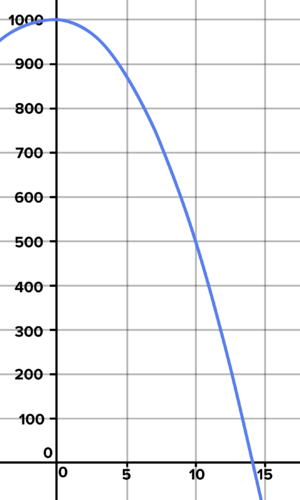
  ::05x2+1000x2=200x_102x=102秒x14.1秒

  播放段落

  Here's the graph:
  ::以下是图表:

  

  播放段落

  Work it Out
  ::工作出来

  播放段落
  1. A rock is dropped from a 1.5-kilometer cliff. Create an equation to model its height as a function of time. Determine its height after 7 seconds. Determine when the rock is 800 meters above the ground. Determine when the rock hits the ground. Graph.
     ::岩石从1.5公里悬崖上坠落。 创建一个方程式, 以时间函数来模拟其高度。 确定7秒后的高度。 确定岩石在地面上方800米。 确定岩石在地面上方。 确定岩石何时撞击地面。 图形 。
  播放段落
  2. A rock is dropped from a 2-kilometer cliff. At the same time, a drone ascends at a constant 30 meters per second. Create equations to model the height of each as a function of time. Graph. Write, but do not solve, an equation to determine when the rock and the drone pass each other. Use graphing or solving technology to answer this question. Determine the height of the drone and the rock at this time. Confirm your results with your graph.
     ::岩石从 2 公里悬崖上坠落。 同时, 无人机以恒定 30 公尺每秒升起。 创建方程式, 将每个高度作为时间的函数来建模。 图表 。 写一个方程, 但不解析, 以决定岩石和无人机何时通过 。 使用图形或解析技术来解答这个问题 。 确定无人机和岩石的高度 。 用图表确认您的结果 。
  播放段落
  3. What are the features of the quadratic equations you were able to solve algebraically in this lesson? Contrast those with the ones you needed to solve using solving or graphing technology. Explain the differences.
     ::您能够在这个课中解析代数方程式的特性是什么? 对比那些公式与您需要用解析或图形化技术解析的公式。 解释差异 。

  播放段落

    Summary
  ::摘要

  播放段落
  • Standard form for a quadratic is  $\begin{array}{r}y=a{x}^2+bx+c.\end{array}$
    ::y=ax2+bx+c 的二次方位标准窗体。
  播放段落
  • When solving quadratic equations, if there are no linear terms, or linear terms are eliminated in the process of solving, the equation can be solved algebraically with the tools you have so far.
    ::当解析二次方程式时,如果没有线性术语,或者在解答过程中消除线性术语,该方程式可以用你迄今拥有的工具进行代数解析。
  播放段落
  • If there are linear terms that are not eliminated, you do not yet have the tools to solve the equation, and the solution can be found using technology.
    ::如果有线性术语没有被删除,那么您还没有解决等式的工具,而解决方案可以使用技术找到。