Course: 4.7 解决线性和非线性不平等和非线性不平等-interactive

Section outline

Select section General

Collapse Expand
General

Collapse all Expand all
- Select activity 新闻通告
  
  新闻通告 Forum
Select section 解决线性和非线性不平等和非线性不平等

Collapse Expand
解决线性和非线性不平等和非线性不平等
The Purpose of this Lesson
::本课程的目的

In this lesson, you will explore, interpret, and solve absolute value inequalities in a graphical and algebraic context. You'll learn various techniques you can use to solve absolute value inequalities.
::在此教训中, 您将探索、解释并解决图形和代数背景下的绝对值不平等。您将学习各种技巧, 以解决绝对值不平等问题。

Introduction: Solving Inequalities
::导言:解决不平等问题

Work it Out
::工作出来

Recall how to solve inequalities in one variable . Practice by solving each of the following. Write each solution interval. Graph each solution on a number line. The first one is done for you as a reminder.
::回顾如何解决一个变量中的不平等问题。练习解决以下每个变量。写入每个解决方案间隔。在数字行上绘制每个解决方案。第一个解决方案是为您完成的, 提醒您。

$\begin{aligned} \begin{array}{ll} a. & 3 x > 6 \\ Divide both sides by 3 to get x > 2 : In interval notation, x = (2, \infty) \end{array} \end{aligned}$
::a.3x>6 双侧除以 3 以获得 x> 2 : 在间距符号中 x= (2, )

$\begin{aligned} \begin{array}{ll} b. & - 4 x + 5 \leq 7 \\ c. & - 3 x + 8 \geq 13 \\ d. & \frac{1}{3} x > \frac{1}{5} x \\ e. & \frac{3}{5} x < \frac{2}{3} x + 8 \\ f. & 3 x + 4 < 3 x + 5 \\ g. & x \geq x \\ h. & 2 x - 5 > 6 x - 15 \\ i. & x \leq 1 \end{array} \end{aligned}$
::b. -4x+5-7c.-3x+8-13d.13x>15x35x <23x+8f.3x+4 <3x+5g.xxxxxh.2x-5>6x-15i.x_1

A wingsuit flier jumps from a 1-kilometer tall cliff and glides along a of $\begin{aligned} - \frac{5}{8} . \end{aligned}$ Create a function to model her location, given that the base of the cliff is at the origin. Write and solve an equation to determine her horizontal distance traveled when she is at a height of 500 meters. Over what interval is her height above 500 meters? Write and solve an inequality to confirm this result. Highlight the points on the line where her height is above 500 meters but less than 1000.
::从1公里高的悬崖上跳下一只翼状浮标, 沿着- 58 的高悬崖滑翔。如果悬崖底部位于原点, 创建一个函数来模拟她的位置。写入并解析一个方程式以确定她高度500米时的横向距离。她的高度在500米以上, 间隔是多少? 写入并解决一个不平等以证实这个结果。突出显示她身高超过500米但不到1000米的线上的点。

Activity 1: Solving Linear Inequalities
::活动1:解决线性不平等

Example 1-1
::例1-1

The solution to an inequality can be interpreted graphically. In the first problem above, you represented the solution to the inequality with a number line. In the second problem, you thought about the solution as the set of $\begin{aligned} x \end{aligned}$ -values that return $\begin{aligned} y \end{aligned}$ -values greater than 500 in the function. Here is a similar scenario to the one you just modeled:
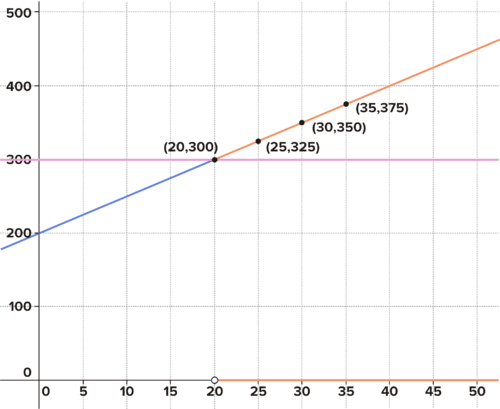
::不平等的解决方案可以用图形方式来解释。在以上第一个问题中,您用数字行代表不平等的解决方案。在第二个问题中,您将解决方案视为返回函数中大于500的 x 值的 x 值组。这里与您刚才模拟的类似方案类似:

A drone is released from the top of a 200 meter building and ascends at 5 meters per second

A drone is released from the top of a 200-meter building. It ascends at 5 meters per second. Create and graph a function to model the scenario. When will the drone reach the 300-meter mark? Write and solve an inequality to determine when the drone will be above 300 meters. Represent this solution on a number line. Represent this on the graph by highlighting the heights corresponding to the solution set .
::无人驾驶飞机从一个200米建筑的顶部释放出来, 升至每秒5米。创建并绘制一个函数来模拟情景。无人驾驶飞机何时到达300米标记? 写入并解决一个不平等问题, 以确定无人驾驶飞机何时会超过300米。在数字线上代表这个解决方案。在图形上代表这个解决方案, 突出显示与设定的解决方案相对应的高度。

Solution: The function is $\begin{aligned} y = 5 x + 200. \end{aligned}$
::解析度: 函数为 y= 5x+200 。

To determine when the drone reaches 300 meters:
::确定无人机何时到达300米:

To determine when the drone will be above 300 meters:
::确定无人机何时将超过300米:

This can be represented on a number line and on the graph. The ray on the $\begin{aligned} x \end{aligned}$ -axis represents all the solutions to the inequality. The graph of the linear function shows the height of the drone over time. The point (20,300) represents the moment when the drone reaches a height of 300. The height of 300 is represented by a horizontal line. The orange ray on the function highlights the heights after 20 seconds. Testing any value greater than 20 in the inequality makes the inequality true. Substituting values for $\begin{aligned} x \end{aligned}$ greater than 20 into the original function returns $\begin{aligned} y \end{aligned}$ -values greater than 300, as shown by the additional points graphed.
::这可以在数字行和图形上表示。 X 轴上的射线代表不平等的所有解决方案。线性函数图显示无人驾驶飞机随时间推移的高度。点(20 300)代表无人驾驶飞机达到高度300的那一刻。高度为300,以水平线表示。函数上的橙色射线显示20秒后的高度。测试任何值大于20的不平等值使不平等成为真实。将20以上x值转换为原始函数返回 y 值大于300,如其他点图表所示。

The point (20, 300) represents the moment when the drone reaches a height of 300 m

Work it Out
::工作出来

A meadow has an area of 300 square meters in year 0. The meadow is increasing in area by 40 square meters every year. Write an equation for the area of the meadow as a function of time. Graph the function. Write and solve an equation to determine when the meadow surpasses an area of 1000 square meters. Write and solve an inequality to determine when the meadow has an area greater than 1000 square meters. Represent the solution graphically using the $\begin{aligned} x \end{aligned}$ -axis as the number line, as in the example above. Find and graph several points that show that values from the solution to the inequality return values greater than 1000 in the original function. Highlight the part of the function that corresponds to the solution to the inequality, as in the example above.
::草地在0年的面积为300平方米。草地每年在面积上增加40平方米。将草地面积写成一个方程式作为时间函数。绘制函数。写入和解析一个方程式, 以确定草地面积何时超过1000平方米。写入和解析一个不平等性方程式, 以确定草地面积何时大于1000平方米。如上例所示, 以 X 轴作为数字线代表解决方案。查找和绘制几个点, 显示在原始函数中, 不平等的解决方案返回值大于1000 。突出显示与不平等解决方案相对应的部分功能, 如上例。

Graph the function $\begin{aligned} y = - \frac{5}{7} x + 12. \end{aligned}$ Solve the inequality $\begin{aligned} - \frac{5}{7} x + 12 \leq 4. \end{aligned}$ Represent the solution graphically using the same two methods applied in the last problem. Use the graph and points on the original function to explain and interpret your solution to the inequality.
::函数 y57x+12。解决不平等 - 57x+124。使用在最后一个问题中使用的相同两种方法以图形方式代表解决方案。使用原始函数上的图形和点来解释和解释您对不平等的解决方案。

  Solving Inequalities in One Variable
::解决一个变量中的不平等

Inequalities can be solved algebraically.
::不平等可以通过代数解决。

Be sure and reverse the direction of the inequality sign when multiplying or dividing both sides by a negative number.
::在将双方乘以负数或除以负数时,要确信并扭转不平等迹象的方向。

The solution to an inequality can be visualized with a number line.
::解决不平等的办法可以用数字线直观地看到。

The solution to an inequality of the form $\begin{aligned} f (x) > a \end{aligned}$ can be visualized as the set of $\begin{aligned} x \end{aligned}$ -values that return $\begin{aligned} y \end{aligned}$ -values greater than $\begin{aligned} a . \end{aligned}$
::f(x)>a 形式的不平等的解决方案可以直观化为返回y值大于a的 x 值组。

Adjust accordingly if the sign is $\begin{aligned} \geq, <, and \leq . \end{aligned}$
::如果标记是 , < 和 ,则相应调整。

Activity 2: Solving Non-Linear Inequalities
::活动2:解决非长期不平等问题

Example 2-1
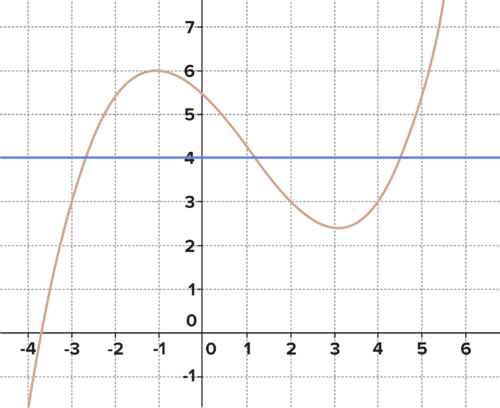
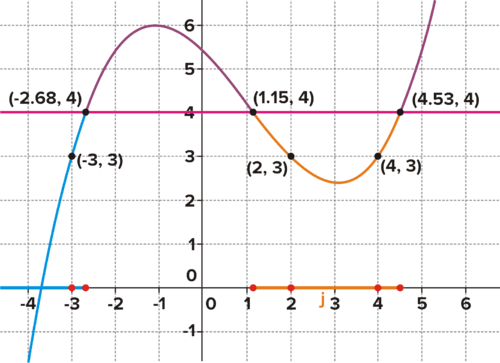
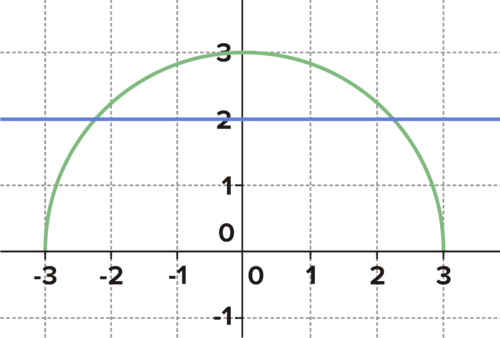
::例2-1

Given the graph of $\begin{aligned} f (x) \end{aligned}$ below, give the approximate solution to the inequality $\begin{aligned} f (x) \leq 4. \end{aligned}$ Represent the solution on a number line.
::鉴于下文f(x)的图表,请大致说明不平等的解决方案f(x)_4.。

Find the approximate solution to f(x) <= 4

Solution:    Based on the graph, there are 3 approximate points where $\begin{aligned} f (x) = 4 : \end{aligned}$
::解答:根据图表,有3个大概点f(x)=4:

Based on the graph, $\begin{aligned} f (x) \leq 4 \end{aligned}$ in the following intervals:
::根据图表,f(x)_4, 间隔如下:

Here is the accurate graphical representation of the original function, including the number line representation along the $\begin{aligned} x \end{aligned}$ -axis, and highlighting the corresponding calculated values for the original function. Several points are shown. For these points, the $\begin{aligned} x \end{aligned}$ -values are in the solution set of the inequality, and they return $\begin{aligned} y \end{aligned}$ -values below 4 in the original function.
::这是原始函数的准确图形表示, 包括 X 轴沿线的数字线表示, 并突出显示原始函数的相应计算值。显示几个点。对于这些点, x 值处于不平等的解决方案中, 它们返回原始函数中的 y 值低于 4 。

f(x) <= 4 highlighted in blue and orange

Interactive
::交互式互动

Use the interactive to adjust the parameters of the inequality. Describe how the solution changes as the parameters change.
::使用互动来调整不平等参数。描述当参数变化时解决方案是如何变化的。

INTERACTIVE

Absolute Value Inequalities

Move the red and blue sliders to adjust the inequality.
::移动红色和蓝色滑块以调整不平等。

Your device seems to be offline.
Please check your internet connection and try again.

+

Do you want to reset the PLIX?

Yes

No

Work it Out
::工作出来

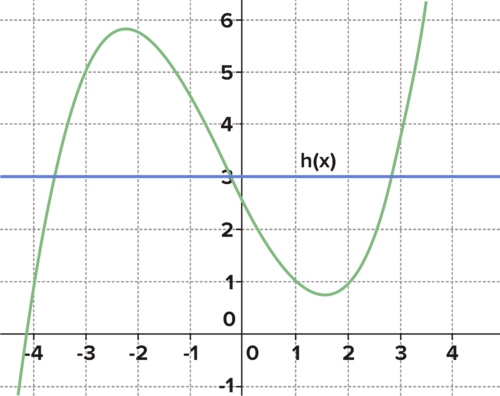
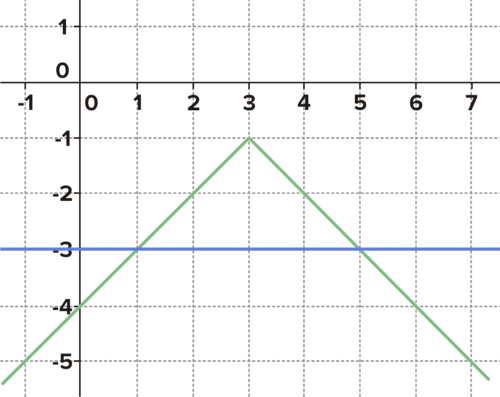
Given the graph of $\begin{aligned} h (x) \end{aligned}$ below, give the approximate solution to the inequality $\begin{aligned} h (x) \geq 3. \end{aligned}$ Represent the solution on a number line.
::鉴于下h(x)图,请大致说明不平等的解决方案 h(x)____________________________________。

What is the approximate solution to h(x) => 3?

Given the graph of $\begin{aligned} g (x) \end{aligned}$ below, give the approximate solution to the inequality $\begin{aligned} g (x) < 2. \end{aligned}$ Represent the solution on a number line.
::考虑到以下 g(x) 的图形,请给出不平等 g(x) < 2. 的大致解决方案。请在数字行中提供解决方案。

What is the approximate solution to g(x) < 2?

Given the graph of $\begin{aligned} f (x) \end{aligned}$ below, give the approximate solutions to the inequality $\begin{aligned} f (x) \geq - 3. \end{aligned}$ Represent the solution on a number line.
::考虑到下文f(x)的图表,请给出解决不平等问题的大致办法f(x)%3。

What are the approximate solutions to f(x) => -3?

Previously, you graphed absolute value functions. Practice by graphing each of the absolute value functions below. Note that each is a composite of a simple absolute value function, y=|x|, and a linear function.
::之前,您绘制了绝对值函数的图示。练习时绘制了以下每个绝对值函数的图示。请注意, 每个绝对值函数都是简单的绝对值函数yx和线性函数的组合。

$\begin{aligned} \begin{array}{ll} a. & f (x) = | x | \\ b. & g (x) = | - x | \\ c. & h (x) = | x - 3 | \\ d. & f (x) = | \frac{1}{3} x | \\ e. & g (x) = | \frac{1}{3} x + 7 | \\ f. & h (x) = | \frac{1}{2} x + 3 | \end{array} \end{aligned}$
:x)\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\

Activity 3: Solving Absolute Value Inequalities Graphically and Algebraically
::活动3:以图形和代数方式解决绝对价值不平等问题

Example 3-1
::例3-1

Given $\begin{aligned} f (x) = | 3 x - 5 |, \end{aligned}$ determine the values for which $\begin{aligned} f (x) = 7. \end{aligned}$ Then determine the values for which $\begin{aligned} f (x) > 7. \end{aligned}$ Support your solution with a graph. Finally, determine the values for which $\begin{aligned} f (x) < 7. \end{aligned}$ Support your solution with a graph. What are the differences and similarities between the solution of $\begin{aligned} | f (x) | > 7 \end{aligned}$ and $\begin{aligned} | f (x) | < 7 ? \end{aligned}$ Generalize your results.
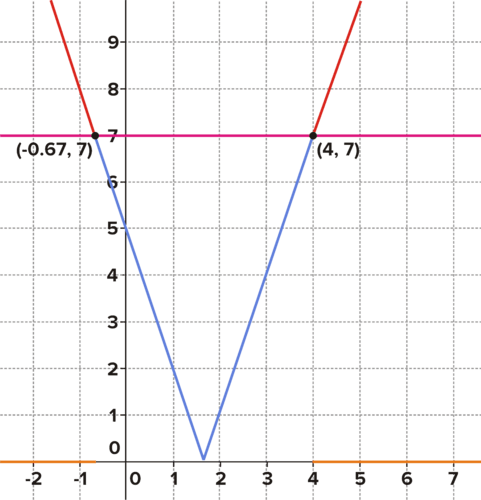
::给定 f( x)\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\

Solution:    If $\begin{aligned} f (x) = 7, \end{aligned}$ then $\begin{aligned} | 3 x - 5 | = 7. \end{aligned}$ This is an absolute value equation. You've solved these in prior lessons. The process is shown below:
::解析 : 如果 f( x) = 7, 那么\\\ 3x - 5\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\>\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\

If $\begin{aligned} f (x) > 7, \end{aligned}$ then $\begin{aligned} | 3 x - 5 | > 7. \end{aligned}$ Solve it graphically, but use the solution to $\begin{aligned} f (x) = 7 \end{aligned}$ to assist you. The graph is shown below. The solution is:
::如果 f( x) > 7, 那么\\\ 3x- 5\\\\\\\ 图形化解决它, 但使用 etf( x)= 7 的解决方案来帮助您。图形显示在下面。解决方案是 :

Given f(x) = |3x - 5|, determine the values for which f(x) =7
::给定 f( x) = 3x - 5 =, 确定 f( x) = 7 的值

If $\begin{aligned} f (x) < 7, \end{aligned}$ then $\begin{aligned} | 3 x - 5 | < 7. \end{aligned}$ Solve it graphically, but use the solution to $\begin{aligned} f (x) = 7 \end{aligned}$ to guide you. The graph is shown below. The solution is:
::如果 f( x) < 7, 那么\\ 3x- 5\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\

$\begin{aligned} \begin{array}{l} - \frac{2}{3} < x < 4 \end{array} \end{aligned}$

::-23 <x <4

Given f(x) = |3x -5| < 7, when f(x) < 7, the solution is -2/3 < x < 4
::给定 f( x) = @ 3x - 5 = < 7 f( x) < 7, 解决方案是 - 2/3 < x < 4

The solution to $\begin{aligned} | f (x) | > 7 \end{aligned}$ was two separate intervals, while the solution to $\begin{aligned} | f (x) | < 7 \end{aligned}$ was a single interval. The endpoints of the intervals were the solutions to $\begin{aligned} | f (x) | = 7. \end{aligned}$
::==============================================================================================================================================*==============================================================================================================================================================================================================================================================================================================================================================================

  Solving Absolute Value Inequalities
::解决绝对价值不平等

Assume $\begin{aligned} f (x) \end{aligned}$ is a linear function and $\begin{aligned} a \end{aligned}$ is positive.
::假设 f( x) 是线性函数, 是正值。

To solve $\begin{aligned} | f (x) | > a : \end{aligned}$
::要解析\\ f( x) { } a :

The solution is both intervals to the left and right of the solutions to $\begin{aligned} | f (x) | = a . \end{aligned}$
::解决方案在 f(x)a 的左右和右边都是间隔。

Solutions are found algebraically by solving $\begin{aligned} f (x) > a \end{aligned}$ or $\begin{aligned} f (x) < - a . \end{aligned}$
::通过解析 f(x) > a 或 f(x) a 找到代数解决方案。

To solve $\begin{aligned} | f (x) | < a : \end{aligned}$
::要解析\\ f( x) { } a :

The solution is the interval between the solutions to $\begin{aligned} | f (x) | = a . \end{aligned}$
::解决方案是 {f(x)}}a 的解决方案之间的间隔。

The solution is found algebraically by solving $\begin{aligned} - a < f (x) < a . \end{aligned}$
::溶液通过解析 -a<f(x)<a) 找到代数。

If the signs are $\begin{aligned} \geq or \leq, \end{aligned}$ the solutions to the inequalities include the solutions to $\begin{aligned} | f (x) | = a . \end{aligned}$
::如果标牌是or,解决不平等的办法包括解决f(x)a。

Interactive
::交互式互动

Use the interactive to explore solving absolute value inequalities algebraically and graphically.
::利用互动来探索如何用代数和图形方式解决绝对价值不平等问题。

INTERACTIVE

Breaking Down Absolute Value Inequalities

Move the points around to change the inequality.
::移动各点来改变不平等。

Change the inequality symbol with the dropdown menu in the original equation.
::用原始方程式中的下拉菜单来更改不平等符号。

Your device seems to be offline.
Please check your internet connection and try again.

+

Do you want to reset the PLIX?

Yes

No

Example 3-2
::例3-2

Solve each of the following absolute value inequalities algebraically:
::以代数方式解决下列绝对值不平等的每一项:

Solution:    The first inequality is:
::解决:第一种不平等是:

From the pattern observed above, values for $\begin{aligned} 2 x - 4 \end{aligned}$ that are either $\begin{aligned} \geq 8 \end{aligned}$   or $\begin{aligned} \leq - 8 \end{aligned}$ will make the inequality true:
::从上述模式来看, 2x-4 的数值, 即8 或% 8 , 将使不平等成为事实:

Values in either of those two intervals make the inequality true. Values in either of those two intervals return values for $\begin{aligned} | 2 x - 4 | \end{aligned}$ that are $\begin{aligned} \geq 8. \end{aligned}$ This solution can be confirmed by testing values, and by graphing.
::这两个间隔中任何一个间隔的数值都使不平等成为真实。如果是 2x-48,这两个间隔的回报值中的任何一个,其数值都是真实的。通过测试值和图形化,可以证实这一解决办法。

The second inequality is:
::第二个不平等是:

From the pattern observed above, values for $\begin{aligned} x + 6 \end{aligned}$ that are between $\begin{aligned} - 10 \end{aligned}$ and $\begin{aligned} 10 \end{aligned}$ will make the inequality true:
::从上述模式来看, x+6 的数值在- 10 和 10 之间,将使不平等成为事实:

$\begin{aligned} - 10 < x + 6 < 10 \end{aligned}$

::- 10 < 10 < x+6 < 10

To solve this inequality, it can be useful to think of it as the set of values that make both the following inequalities true:
::为了解决这种不平等,不妨将它视为使以下不平等既真实又真实的一套价值观:

$\begin{aligned} \begin{array}{lcl} - 10 < x + 6 & and & x + 6 < 10 \\ - 16 < x & and & x < 4 \\ - 16 < x < 4 \end{array} \end{aligned}$

::- 10 < 10 < x+6andx+6 < 10 - 16 < xandx < 4 - 16 < 4 > < 4

Any value in that interval makes the inequality true. Any value in that interval returns values for $\begin{aligned} | x + 6 | \end{aligned}$ that are $\begin{aligned} < 10. \end{aligned}$ This solution can be confirmed by testing values, and by graphing.
::此间隔中的任何值都会使不平等成为真实。此间隔中的任何值返回 < 10 > 的 {x+6\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\

Work it Out
::工作出来

Solve each of the following. Confirm your solutions by substituting or graphing.
::解决以下各点。通过替换或图形化来确认您的解决方案。

$\begin{aligned} \begin{array}{ll} a. & | x | > 9 \\ b. & | x - 6 | \leq 7 \\ c. & | - \frac{2}{3} x - 2 | < 10 \\ d. & | \frac{4}{5} x + \frac{1}{2} | \geq 2 \\ e. & | x | > - 2 \\ f. & | x | < - 2 \end{array} \end{aligned}$

::=======================================================================================================================================================================================================================================================

  Summary
::摘要

Given $\begin{aligned} f (x) \end{aligned}$ is a linear function and $\begin{aligned} a > 0 : \end{aligned}$

Solutions to $\begin{aligned} | f (x) | > a \end{aligned}$ are found by solving $\begin{aligned} f (x) > a \end{aligned}$ or $\begin{aligned} f (x) < a . \end{aligned}$
::用于 \ f( x) {a) 的解决方案通过解析 f( x) > a 或 f( x) < a 找到。

Solutions to $\begin{aligned} | f (x) | < a \end{aligned}$ are found by solving $\begin{aligned} - a < f (x) < a . \end{aligned}$
::%f(x)a 的解决方案通过解析 -a<f(x)<a) 找到。

::给定 f( x) 是线性函数和 a > 0 : 通过解析 f( x) > a 或 f( x) < a 找到 \ f ( x) { ) a 的解决方案。给定 f( x) {a 的解决方案是通过解析 < a < f( x) < a 找到。

The endpoints of the solution intervals are the $\begin{aligned} x \end{aligned}$ -values where $\begin{aligned} | f (x) | = a . \end{aligned}$
::溶液间隔的终点是 {(x)}}}a 的 x 值。

These endpoints are included in the solution set when the inequality sign is $\begin{aligned} \geq or \leq . \end{aligned}$
::当不平等标志为_________或_________时,这些终点就包括在设定的解决方案中。

4.7 解决线性和非线性不平等和非线性不平等-interactive

Section outline

General

解决线性和非线性不平等和非线性不平等

The Purpose of this Lesson
::本课程的目的

Introduction: Solving Inequalities
::导言:解决不平等问题

Work it Out
::工作出来

Activity 1: Solving Linear Inequalities
::活动1:解决线性不平等

Example 1-1
::例1-1

Work it Out
::工作出来

Solving Inequalities in One Variable
::解决一个变量中的不平等

Activity 2: Solving Non-Linear Inequalities
::活动2:解决非长期不平等问题

Example 2-1
::例2-1

Interactive
::交互式互动

Work it Out
::工作出来

Activity 3: Solving Absolute Value Inequalities Graphically and Algebraically
::活动3:以图形和代数方式解决绝对价值不平等问题

Example 3-1
::例3-1

Solving Absolute Value Inequalities
::解决绝对价值不平等

Interactive
::交互式互动

Work it Out
::工作出来

Summary
::摘要

Section outline

General

解决线性和非线性不平等和非线性不平等

The Purpose of this Lesson ::本课程的目的

Introduction: Solving Inequalities ::导言:解决不平等问题

Work it Out ::工作出来

Activity 1: Solving Linear Inequalities ::活动1:解决线性不平等

Example 1-1 ::例1-1

Work it Out ::工作出来

Solving Inequalities in One Variable ::解决一个变量中的不平等

Activity 2: Solving Non-Linear Inequalities ::活动2:解决非长期不平等问题

Example 2-1 ::例2-1

Interactive ::交互式互动

Work it Out ::工作出来

Activity 3: Solving Absolute Value Inequalities Graphically and Algebraically ::活动3:以图形和代数方式解决绝对价值不平等问题

Example 3-1 ::例3-1

Solving Absolute Value Inequalities ::解决绝对价值不平等

Interactive ::交互式互动

Work it Out ::工作出来

Summary ::摘要

The Purpose of this Lesson
::本课程的目的

Introduction: Solving Inequalities
::导言:解决不平等问题

Work it Out
::工作出来

Activity 1: Solving Linear Inequalities
::活动1:解决线性不平等

Example 1-1
::例1-1

Work it Out
::工作出来

Solving Inequalities in One Variable
::解决一个变量中的不平等

Activity 2: Solving Non-Linear Inequalities
::活动2:解决非长期不平等问题

Example 2-1
::例2-1

Interactive
::交互式互动

Work it Out
::工作出来

Activity 3: Solving Absolute Value Inequalities Graphically and Algebraically
::活动3:以图形和代数方式解决绝对价值不平等问题

Example 3-1
::例3-1

Solving Absolute Value Inequalities
::解决绝对价值不平等

Interactive
::交互式互动

Work it Out
::工作出来

Summary
::摘要