4.8 具有常数的四方-interactive

Section outline

• Select section General

  Collapse Expand

  General

  Collapse all Expand all

  • Select activity 新闻通告

    

    新闻通告 Forum
• Select section 具有常数条件的四边形

  Collapse Expand

  具有常数条件的四边形

  播放段落

  The Purpose of This Lesson
  ::本课程的目的

  播放段落

  In this lesson,  you will model scenarios with quadratic functions featuring a constant term . You'll by using the properties of equality and reversing operations . You'll find the parameters for quadratic functions from given points and use these techniques to create quadratic models.
  ::在此课中, 您将模拟带有二次函数的情景, 以一个恒定的句号 。 您将使用平等属性和反转操作。 您可以从给定点找到二次函数的参数, 并使用这些技术创建二次函数模型 。

  ---

  播放段落

  Activity  1: Solving Quadratic Equations to Answer Questions About Functions
  ::活动1:解决关于函数的解答问题方等量

  播放段落

  Work it Out
  ::工作出来

  播放段落
  1. The equation for the height of an object as a function of time is  $\begin{align*}h(x)=\frac12 a x^2 +v_0 x +h_0,\end{align*}$  where  $\begin{align*}a\end{align*}$  is the acceleration,  $\begin{align*}v_0\end{align*}$  is the initial velocity, and  $\begin{align*}h_0\end{align*}$  is the initial height. Acceleration due to gravity is approximately -10 meters per second, per second. If an object is dropped from a height of 2.4 kilometers, give a function for its height over time, neglecting air resistance. Graph the function. Write and solve an equation to determine when the object has a height of 1.2 kilometers. Write and solve an equation to determine when the object hits the ground. What is this point on the graph called? Give the practical domain and range for this scenario.
     ::物体高度的方程式是 h( x) = 12ax2+v0x+h0, 其中加速度为加速度, v0 是初始速度, h0 是初始高度。 重力加速大约 - 10米每秒, 秒。 如果一个物体从2.4公里高度下降, 则在时间高度上设定一个函数, 忽略空气阻力 。 绘制函数 。 写入并解析一个方程式, 以确定该对象何时高度为1.2公里。 写入并解析一个方程式, 以确定该对象何时撞击地面。 图形上请使用哪个点? 给出此情景的实际域和范围 。

  

  播放段落
  2. Brandon wants to make a crop circle of a certain area and wants to know the radius required. The area of a circle is given by the equation  $\begin{align*}A=\pi r^2.\end{align*}$  Graph over the domain  $\begin{align*}[0,10].\end{align*}$  Brandon wants his crop circle to have an area of 50 square meters. Write and solve an equation to determine the radius required. If Brandon doubles the radius, how does this impact the area of the circle? Explain.
     ::布兰登想要在一定区域中建立作物圈, 并想知道所需的半径。 一个圆的面积由域[ 0, 10] 的方程式 Ar2. 图给出。 布兰登想要他的作物圈有50平方米的面积。 写入和解析一个方程式以确定所需的半径。 如果布兰登将半径增加一倍, 这会如何影响圆的面积? 解释 。
  播放段落
  3. Given the following quadratic functions, write and solve an equation to determine when the function returns a value of 12. Write and solve an equation to determine the  $\begin{align*}x\end{align*}$ - intercepts . Sketch the graphs of each, showing the vertex , and showing solutions to the above equations. Note that it is possible that some equations you write will have no solutions, one solution, or two solutions.
     ::根据以下的二次函数, 写入并解析一个方程, 以确定函数返回值为 12 。 写入并解析一个方程以决定 x 界面。 绘制每个方程的图形, 显示顶点, 并显示上述方程的解决方案 。 请注意, 您写入的某些方程可能没有解决方案、 一种解决方案或两种解决方案 。

  播放段落

  $\begin{align*}\qquad \quad\begin{array}{ll} \text{a.} &f(x)=3x^2-15\\ \text{b.} &g(x)=x^2\\ \text{c.} &h(x)=-\frac12 x^2\\ \text{d.} &f(x)=-2x^2+12\\ \text{e.} &g(x)=\frac{1}{10} x^2+1\\ \text{f.} &h(x) -\frac{1}{5} x^2 +1\\ \end{array}\end{align*}$
  ::a.f(x) = 3x2 - 15b.g(x) =x2c.h(x) =x12x2d.f(x) =2x2+12e.g(x) =110x2+1f.h(x) - 15x2+1

  播放段落
  4. Based on your work in the previous problem, is it true that if a quadratic has a vertex on the  $\begin{align*}y\end{align*}$ -axis, it has the form  $\begin{align*}y=ax^2+c? \end{align*}$  How do you know?
     ::根据你对前一个问题的工作 是否真的有 象形在 Y 轴上, 它有y= ax2+c 的形状? 你怎么知道?

  播放段落

  Example 1-1
  ::例1-1

  播放段落

  In the above problems you solved equations involving functions of the form:
  ::在上述问题中,您解决了涉及表格功能的方程式:

  播放段落

  $$\begin{align*}f(x)=ax^2+c\end{align*}$$
  :xx) = 轴2+c

  播放段落

  You solved equations of two different forms shown below, where sometimes  $\begin{align*}c\end{align*}$  was 0:
  ::您解答了以下两种不同形式的方程式, 有时c是0:

  播放段落

  $$\begin{align*}\quad\begin{array}{ll} 1. &ax^2+c=d\\ 2.&ax^2+c=0\\ \end{array}\end{align*}$$
  ::1.aax2+c=d2.ax2+c=0

  播放段落

  Describe the form for the function. Explain how changing the parameters  $\begin{align*}a\end{align*}$  and  $\begin{align*}c\end{align*}$  impacts the graph of the function. Solve each of the equations above. Explain how changing the parameters  $\begin{align*}a\end{align*}$ ,  $\begin{align*}c\end{align*}$  and  $\begin{align*}d\end{align*}$  impacts the solution of the equations.
  ::描述函数的窗体。解释参数 a 和 c 的变化如何影响函数的图形。 解析上面的每一个方程式。 解释参数a、 c 和 d 的变化如何影响方程式的解决方案 。

  播放段落

  Solution:    The function  $\begin{align*}f(x)=ax^2+c\end{align*}$   is a quadratic function that can be described two different ways:
  ::解析度: 函数 f( x) = ax2+c 是一个可描述两种不同方式的二次函数 :

  播放段落

  $$\begin{align*}\begin{array}{l|l|l|l} \text{Function} & \text{General Equation} & \text{Explanation}\\ \hline f(x)=ax^2+c & y=ax^2+bx+c & \text{The function is in standard form: }b=0.\\ f(x)=ax^2+c & y=a(x-h)^2+k & \text{The function is in vertex form: }h=0.\\ \end{array}\end{align*}$$
  ::函数 EquationExplainationf(x) = 轴2+ cy= 轴2+bx+c 函数以标准形式显示 : b=0.f(x) = 轴2+cy=a(x-h) 2+k 函数以顶部形式显示 : h=0 。

  播放段落

  To solve  $\begin{align*}ax^2+c=d:\end{align*}$
  ::要解析 ax2+c=d:

  播放段落

  $$\begin{align*}\begin{array}{l} ax^2+c=d\\ ax^2=d-c\\ x^2=\frac{d-c}{a}\\ x=\pm \sqrt{\frac{d-c}{a}} \end{array} \end{align*}$$
  ::ax2+c=dax2=d-cx2=d-cx2=d-cax*d-cax*d-ca

  播放段落

  If  $\begin{align*}\frac{d-c}{a}\end{align*}$  is negative, there is no solution. This happens when  $\begin{align*}d-c\end{align*}$  is negative and  $\begin{align*}a\end{align*}$  is positive, or vice versa.
  ::如果 d-ca 是负的, 就没有解决办法。 当 d- c 是负的, 而 a 是正的, 或者反之亦然, 就会发生这种情况 。

  播放段落

  If  $\begin{align*}\frac{d-c}{a}\end{align*}$  is 0, there is one solution, 0. This happens when  $\begin{align*}d-c\end{align*}$  is 0.
  ::如果 d-ca 是 0, 只有一个解决方案, 0。 当 d- c 是 0 时会发生这种情况 。

  播放段落

  To solve  $\begin{align*}ax^2+c=0:\end{align*}$
  ::要解析 ax2+c=0 :

  播放段落

  $$\begin{align*}\begin{array}{l} ax^2+c=0\\ ax^2=-c\\ x^2=\frac{-c}{a}\\ x=\pm \sqrt{\frac{-c}{a}}\\ \end{array}\end{align*}$$
  ::ax2+c=0ax2cx2cax*cax *cax*ca=0ax2cx2cx2cax*cax*ca

   

  播放段落

  If  $\begin{align*}\frac{-c}{a}\end{align*}$  is negative, there is no solution. This happens when  $\begin{align*}c\end{align*}$  and  $\begin{align*}a\end{align*}$  have the same sign.
  ::如果 -ca 是负的, 就没有解决办法。 当 c 和一个符号相同时, 就会发生这种情况 。

  播放段落

  If  $\begin{align*}\frac{-c}{a}\end{align*}$  is 0, there is one solution, 0. This happens when  $\begin{align*}c\end{align*}$  is 0.
  ::如果 -ca 是 0, 只有一个解决方案, 0。 当 c 是 0 时会发生这种情况 。

  播放段落

     Quadratic Functions with No Linear Term
  ::无线性期的二次曲线函数

  播放段落

  A quadratic of the form  $\begin{align*}y=ax^2+c\end{align*}$  is in both standard and vertex form.
  ::y=ax2+c 窗体的二次曲线以标准形式和顶点形式出现。

  播放段落

  The vertex is  $\begin{align*}(0,c).\end{align*}$
  ::顶点为( 0, c) 。

  播放段落

  Any equation of the form  $\begin{align*}ax^2+c=d\end{align*}$  can be solved using properties of equality and inverse operations.
  ::窗体x2+c=d 的任何方程式都可以使用平等和反向操作的属性来解决。

  播放段落

  The result may be 0,1, or 2 solutions.
  ::结果可能是 0、 1 或 2 个解决方案 。

  ---

  播放段落

  Activity 2: Finding the Equation for a Quadratic Function from Points
  ::活动2:从点寻找二次函数的等量

  播放段落

  Example 2-1
  ::例2-1

  播放段落

  Acceleration due to gravity is different on different planets. Sheri visits several planets and drops objects on each one from a height of 100 meters. Here is a table showing when they hit the surface of each planet. Find the acceleration due to gravity on each planet.
  ::由于重力加速在不同行星上是不同的。 Sheri 访问多个行星,并将天体从100米的高度投到每个行星上。这里的表格显示它们撞击每个行星的表面的时间。查找每个行星的重力加速度。

  播放段落

  $$\begin{align*}\begin{array}{l|l} \text{World} & \text{Time to ground (seconds)}\\ \hline \text{Mercury} & 7.4\\ \text{Venus} & 4.7\\ \text{Earth} & 4.5\\ \text{Earth's Moon} & 11\\ \text{Mars} & 7.4\\ \text{Jupiter} & 2.8\\ \text{Saturn} & 4.4\\ \text{Uranus} & 4.8\\ \text{Neptune} & 4.2\\ \text{Pluto} & 18\\ \text{Ceres} & 27\\ \end{array}\end{align*}$$
  ::地球的月球 火星 7.4Jupiter 2.8Saturn4.4.Uranus4.8Neptune4.2Pluto18Ceres27

    

  播放段落

  Solution:    The general equation  $\begin{align*}h(x)=\frac12 a x^2 +v_0 x +h_0\end{align*}$  can be used. You know  $\begin{align*}h_0=100, \end{align*}$  and there is no initial velocity:
  ::解析度: 可以使用普通等式 h( x) = 12ax2+v0x+h0。 您知道 h0= 100, 没有初始速度 :

  播放段落

  $$\begin{align*}h(x)=\frac12 ax^2+100\end{align*}$$
  ::h(x) = 12ax2+100

  播放段落

  For each planet, you know the time it takes for the object to hit the ground. It's height when it hits the ground is 0.  Taking Mercury as an example:
  ::对于每个行星来说,你知道物体撞击地面需要多少时间。 当物体撞击地面时高度是0。以汞为例:

  播放段落

  $$\begin{align*}\begin{array}{l|l} \text{Equation} & \text{Explanation}\\ \hline \frac12a(7.4)^2+100=0 & \text{Substituting known values for }x \text{ and }y.\\ \frac12(7.4)^2 a+100=0 & \text{Commutative property.}\\ 27.38a+100=0 & \text{Simplifying.}\\ a\approx-3.7 ~\frac{m}{s^2}& \text{Solving.}\\ \end{array} \end{align*}$$
  ::quationExplantation12a(7.4)2+100=0 替代x和y.12(7.4)2a+100=0商品财产的已知价值。

  播放段落

  The same process can be used to find gravity for the remaining planets. Here is acceleration due to gravity on several worlds: 
  ::同样的过程可以用来寻找剩余行星的重力。这里是多个世界的重力加速度:

  播放段落

  $$\begin{align*}\begin{array}{l|l} \text{World} & \text{Gravity} \left(\frac{m}{s^2}\right)\\ \hline \text{Mercury} & -3.7\\ \text{Venus} & -8.9\\ \text{Earth} & -9.8\\ \text{Earth's Moon} & -1.6\\ \text{Mars} & -3.7\\ \text{Jupiter} & -25\\ \text{Saturn} & -10.4\\ \text{Uranus} & -8.7\\ \text{Neptune} & -11.2\\ \text{Pluto} & -0.62\\ \text{Ceres} & -0.27\\ \end{array}\end{align*}$$
  ::世界重力(ms2) 汞-3.7Venus-8.9 地球-9.8 地球的月球-1.6 Mars-3.7 Jupiter-25Saturn-10.4 Uranus-8.7Neptune-11.2Pluto-0.62Ceres-0.27

  播放段落

  Work it Out
  ::工作出来

  播放段落
  1. Given a quadratic of the form  $\begin{align*}f(x)=ax^2+c.\end{align*}$  Each problem below represents a new quadratic. Use the given information to determine the equation for the quadratic. The given information  will include an ordered pair that makes the equation true. Sketch a graph to assist you if needed.
     ::给定了 f( x) = ax2+c 的二次方位。 下面的每个问题代表一个新的二次方位。 使用给定的信息来决定二次方程。 给定的信息将包括一对定购的对方, 使方程成为真实。 如果需要, 请绘制一个图表来帮助您 。

  播放段落

  $\begin{align*}\qquad \quad\begin{array}{ll} \text{a.} & c=5; (9,0)\\ \text{b.} & c=-12; (-4,0)\\ \text{c.} & c=0; (1,8)\\ \text{d.} & (0,11); (-6,0)\\ \text{e.} & (0,7); (7,0)\\ \end{array}\end{align*}$
  ::a.c=5;(9,0)b.c=12;(4,0)c=0;(1,8)d.(0,11);(6,0)e.(0,7);(7,0)

  播放段落
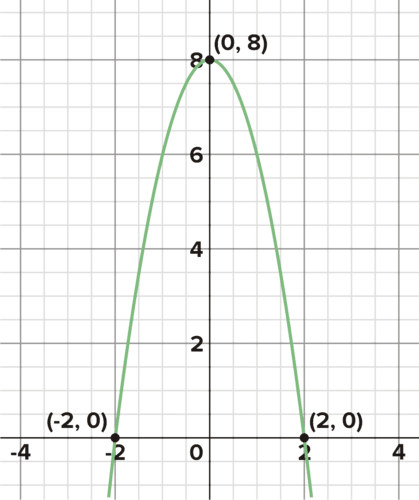
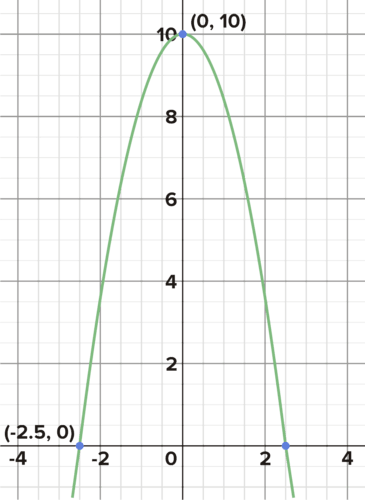
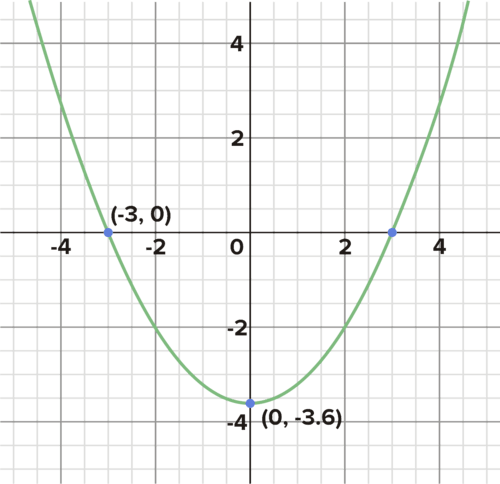
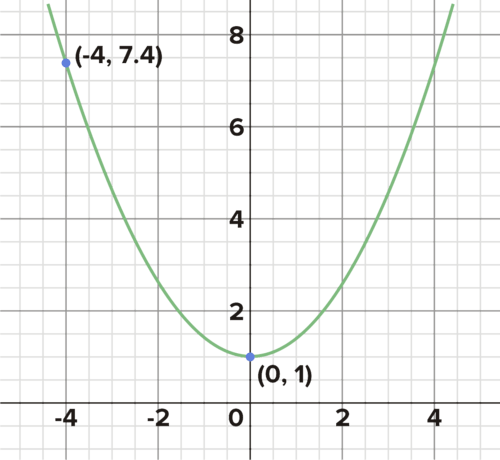
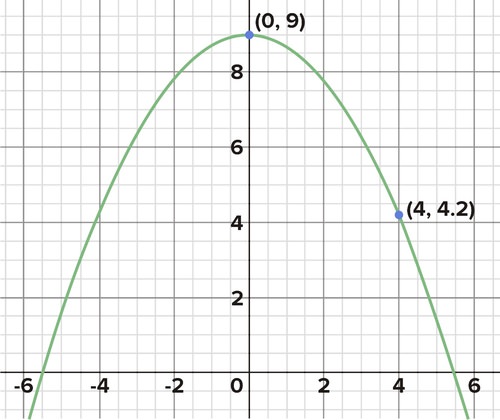
  2. The graphs of several quadratics are given below. Use the labeled points to find the equations for each.
     ::下面列出了几个二次方形的图形。使用标记的点来查找每个方程的方程。

  

  

  

  

  

  播放段落
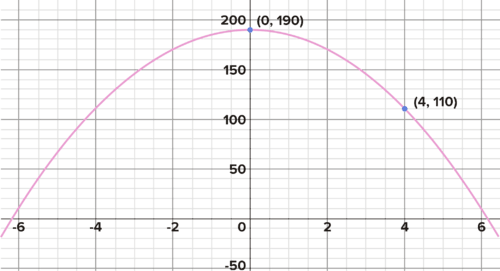
  3. The height of a dropped or thrown object over time can be modeled with a quadratic. But it's also true that if an object is given a horizontal initial velocity, the arc of its travel can also be modeled with a quadratic. If you toss a baseball or football, its vertical motion changes in accordance with the equation for  height  as a function of time.  But its two-dimensional position can be modeled with a quadratic. The following quadratic models the path of a baseball, neglecting air resistance. Find the equation of the parabola from the labeled points.
     ::随时间推移, 抛落或抛弃物体的高度可以用二次方位模型模拟。 但是, 如果给一个对象以水平初始速度, 其飞行的弧也可以用二次方位模型模拟。 如果您投球或足球, 它的垂直运动会随着时间的函数高度的方程而改变。 但是, 它的二维位置可以用二次方位模型模拟。 以下的二次方位模型可以模拟棒球的路径, 忽略了空气阻力。 从标签点找到parbola的方位 。

  

  播放段落

     Finding Equations for Quadratics From Points
  ::从点寻找四面形的方形等量

  播放段落

  If you are given  a specialized form for the quadratic, for example,  $\begin{align*}f(x)=ax^2+c,\end{align*}$  this simplifies your efforts.
  ::如果给您给四边形(例如 f( x) = ax2+c) 指定了专门的表单,这将简化您的努力。

  播放段落

  If you are given a parameter , for example  $\begin{align*}a\end{align*}$  or  $\begin{align*}c,\end{align*}$  this simplifies your efforts.
  ::如果给您给定了一个参数,例如 a 或 c,这将简化您的努力。

  播放段落

  If you are then given an ordered pair on the graph of the quadratic, substitute those values for  $\begin{align*}x\end{align*}$  and  $\begin{align*}y\end{align*}$  to solve for the unknown parameter.
  ::如果在二次曲线图上给您定了一对定单,则用这些数值替代 x 和 y 来解析未知参数。

  播放段落

  Finally, write the function with the known values for the parameters.
  ::最后,用已知参数值写入函数。

  ---

  播放段落

  Activity 3 : Finding Equations for Quadratics From Points When Two Parameters Are Unknown
  ::活动3:在两个参数未知时从点到点寻找四重方形的方形等量

  播放段落

  In the previous problems, you were always provided the vertex of the parabola, that is, the constant term for  $\begin{align*}f(x)=ax^2+c.\end{align*}$  It is possible to find the equation for a quadratic of this form given any two points.
  ::在先前的问题中, 您总是得到抛物线的顶点, 即 f( x) = ax2+c 的常数值。 在任何两个点中, 都可以找到这种形态的二次方程 。

  播放段落

  Example 3-1
  ::例3-1

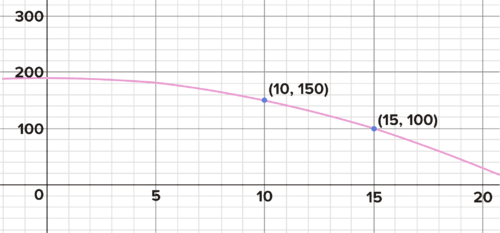
  播放段落

  Jayden is a detective, and one day he finds a bag of gold coins near an apartment building! Clearly, someone had been running away with it and dropped it. He wants to return  it to its owner, but when he asks the residents, several people living on several floors claim it's theirs. All claim the bag was  catapulted out of the window horizontally by an aspiring thief.  Jayden uses his detective skills to access a security camera on the street that is triggered by motion. The camera was triggered the night before by the bag falling from the window of one of the apartments! Unfortunately, the camera only captured two images of the bag moving along a parabolic arc. The first position recorded was a point 10 meters from the base of the building and 150 meters up. The second position was 15 meters from the base and 100 meters up. Jayden reasons that if he can find the equation of the parabola, he can find its vertex, and thus know the window from which the bag was pushed. Remember, the bag was pushed out horizontally, so its height never increased above the height of the window from which it was pushed. Sketch a rough graph. Find the parameters for the function, then write the function that models the path of the bag of coins. Find the vertex. Use your equation to find where the bag likely landed, so that Jayden can see if there is any evidence at the landing spot.
  ::贾登是一名侦探,有一天他在公寓大楼附近找到一袋金币。 显然,有人拿着它跑掉了,然后扔了它。 他想把它还给主人,但他想要把它还给主人。 当他询问居民时,几个住在几层的人声称这是他们的。 所有人都声称袋子是被一个有野心的小偷从窗户上横向射出。 贾登利用他的侦探技能进入街上由运动引发的安全摄像头。 相机是前一天晚上被从公寓的窗户掉下来的袋子触发的。 不幸的是, 相机只捕捉了两个袋子的图像, 沿着抛光弧弧向方向移动。 记录的第一个位置是离大楼底部10米处, 向上150米处。 第二个位置是距基地15米, 向上100米处。 杰登说如果他能找到抛光的方程式, 他可以找到它的脊椎, 从而知道袋子被推出的窗子。 记住, 袋子是水平推出的, 因此, 它的高度从来没有超过窗户的高度。 记录的第一个位置是离大楼的高度, 。 找到一个平面的平方形图。

  播放段落

  Solution:    Since the vertex is on the $\begin{align*}y\end{align*}$ -axis, you know it has the form  $\begin{align*}y=ax^2+c.\end{align*}$  You are not given either of the two parameters. However, you know two points on the parabola: (10,150) and (15,100). Substituting gives two equations:
  ::解答: 因为顶端在它们轴上, 您知道它有 y= ax2+c 的形状。 您没有得到这两个参数中的任何一个。 但是, 您知道抛物线上的两点 : (10, 150) 和 (15, 100) 。 替换给出两个方程式 :

  播放段落

  $$\begin{align*}\begin{array}{l} a(10)^2+c=150\\ a(15)^2+c=100\\ \end{array}\end{align*}$$
  ::a(10)2+c=150a(15)2+c=100

  播放段落

  This is a system of equations because  $\begin{align*}a\end{align*}$  and  $\begin{align*}c\end{align*}$  represent the same values in both equations. And with a bit of arithmetic and re-arranging, you can see it's a linear system:
  ::这是一个方程式系统, 因为一个和 c 代表两个方程式中的相同值。 而且如果略加计算和重新排列, 你可以看到它是一个线性系统 :

  播放段落

  100 a + c = 150 225 a + c = 100

  $$\begin{align*}\begin{array}{l} 100a+c=150\\ 225a+c=100\\ \end{array}\end{align*}$$
  ::100a+c=1502225a+c=100

  播放段落

  Solving the system by subtracting gives:
  ::以减法解决系统, 提供 :

  播放段落

  − 125 a = 50 a = − 2 5 100 ( − 2 5 ) + c = 150 c = 190 f ( x ) = − 2 5 x 2 + 190

  $$\begin{align*}\begin{array}{l} -125a=50\\ a=-\frac{2}{5}\\ \\ 100\left(-\frac{2}{5} \right)+c=150\\ c=190\\ \\ f(x)=-\frac{2}{5} x^2+190\\ \end{array}\end{align*}$$
  ::- 125a=50a=25100(- 25)+c=150c=190f(x)=25x2+190

  

  播放段落

    The owner of the apartment 190 meters up will get their bag of gold back!
  ::房主在190公尺高的地方 就能拿回他们的金包!

  播放段落

     Finding Equations for Quadratics from Points when Two Parameters are Unknown
  ::在两个参数为未知时从点查找四方形的方形

  播放段落

  Given a quadratic of the form  $\begin{align*}y=ax^2+c,\end{align*}$   and two points on its graph:
  ::以 y= ax2+c 形状的二次方位, 以及其图表上的两点表示 :

  播放段落
  • Substitute the ordered pairs for  $\begin{align*}x\end{align*}$  and  $\begin{align*}y,\end{align*}$  and write the resulting linear equations as a system.
    ::以 x 和 y 替代定购的配对, 并将由此产生的线性方程写成一个系统 。
  播放段落
  • Solve the system for  $\begin{align*}a\end{align*}$  and  $\begin{align*}c.\end{align*}$  
    ::解决一个和C的系统。
  播放段落
  • Use these parameters to write the equation for the function.
    ::使用这些参数来写入函数的方程式。

  播放段落

  Interactive
  ::交互式互动

  播放段落

  In the interactive below, move the red points to experiment with changing the parameters for a quadratic of the form $\begin{align*}f(x)=a{x}^{2}+c.\end{align*}$  First find two different quadratics that intersect point $\begin{align*}A\hspace{1mm}(−2,−4) \end{align*}$  on the graph. Next, find two different quadratics that intersect point $\begin{align*}B\hspace{1mm}(4,2)\end{align*}$  on the graph. Lastly, find quadratic that intersects both points $\begin{align*}A\end{align*}$  and $\begin{align*}B.\end{align*}$  Under what conditions is it possible to create two different quadratics of the form $\begin{align*}f(x)=a{x}^{2}+c \end{align*}$  that intersect both $\begin{align*}A\end{align*}$  and  $\begin{align*}B\hspace{1mm}?\end{align*}$
  ::在以下互动点中,移动红点以实验修改 f(x) = ax2+c 窗体的四方形参数。 首先在图形中找到两个相交点A(-2) - 4) 的不同的四方形。 下一步, 在图形中找到两个相交点B( 4) 的四方形。 最后, 找到两个相交点A 和 B。 在什么条件下可以创建 F(x) = ax2+c 的两种不同方形?

  播放段落

  Work it Out
  ::工作出来

  播放段落
  1. A camera records two points on the parabolic path of a baseball. Let the vertex be on the  $\begin{align*}y\end{align*}$ -axis of our model and the origin at ground level. The units for the axes are meters.  T he points the camera records are (50, 80) and (70,60). Sketch a graph. Find the equation for the path of the baseball.  Find its maximum height.  Find where it hits the ground.  Find where it left the ground.  Find the total horizontal distance traveled. 
     ::相机记录棒球的抛物线路径上的两点。 让顶点位于模型的 Y 轴上, 并位于地面。 轴的单位为米。 相机记录点为( 50, 80) 和( 70, 60) 。 绘制一个图。 查找棒球路径的方程 。 查找其最大高度 。 查找它击中地面的位置 。 查找它离开地面的位置 。 查找整个水平距离 。
  播放段落
  2. A sculptor wants to make an arch over her town that just clears the tops of two buildings.   Let the vertex be on the  $\begin{align*}y\end{align*}$  axis of our model and the origin at ground level.   The units for the axes are meters. The tops of the two buildings are at (200, 120) and (-130, 180). Find the equation for the arch.  Find its maximum height.  Find the points where the sculpture hits the ground.  Find the distance between those two points.
     ::雕塑家想在她的城镇上画一个拱门, 划清两座建筑物的顶部。 让顶点在我们模型的 Y 轴上, 从地面开始。 轴的单位是米。 两座建筑物的顶部是( 200, 120) 和( 130, 180) 。 查找拱门的方程。 查找其最大高度 。 找到雕塑撞击地面的点 。 找出这两个点之间的距离 。
  播放段落
  3. A rock is dropped from 1.7 kilometers.  Estimate the acceleration of gravity at 10 meters per second per second and neglect air resistance. At the same time, a drone ascends from the ground with a constant acceleration of 4 meters per second per second. Write equations that model the height of each as a function of time. Write and solve an equation to determine when they have the same height. Sketch a graph for this data. Determine when the rock hits the ground, and when the drone achieves the initial height of the rock.
     ::岩石从 1. 7 公里处坠落。 估计重力加速度为每秒10米, 忽略空气抵抗力。 与此同时, 无人驾驶飞机从地面上升, 恒定加速度为每秒4米。 写方程式, 以每个高度作为时间函数。 写入和解析一个方程式, 以确定它们何时具有相同的高度 。 为此数据绘制一个图表 。 确定当岩石撞击地面时, 以及当无人驾驶飞机到达岩石初始高度时 。
  播放段落
  4. Given each pair of quadratic functions below, determine their intersection points, if they exist. Sketch a rough graph to support your conclusions and explain the number of solutions in the context of the graph.
     ::考虑到以下每对二次函数, 如果存在, 请确定其交叉点 。 绘制一个粗略的图表来支持您的结论, 并在图表中解释解决方案的数量 。

  播放段落

  $\begin{align*}\qquad \quad\begin{array}{l|l|l} \text{a.} & y=x^2 & y=2x^2+7\\ \text{b.} & y=x^2 & y=-2x^2+7\\ \text{c.} & y=\frac13 x^2 &y=\frac12 x^2 -10\\ \text{d.} & y=2x^2 & y=3x^2+10\\ \text{e.} & y=\frac15 x^2 &y=\frac13 x^2\\ \text{f.} & y=-\frac{2}{3} x^2 -10 & y=-\frac23 x^2 -11\\ \end{array}\end{align*}$
  ::a.y=x2y=2x2+7b.y=2x2+7b.y=2x2y=12x2-10d.y=2x2y=3x2+10e.y=15x2y=13x2f.y=23x2-10y=23x2-11

  播放段落
  5. Create equations for two quadratics that do not intersect. Create two that intersect in one point. Create two that intersect in two points.
     ::创建两个不交叉的二次方程。 创建两个在一个点中交叉的二次方程。 创建两个在两个点中交叉的二次方程。
  播放段落
  6. Are the points (10,0) and (-10,0) sufficient to determine a unique equation for a quadratic of the form  $\begin{align*}y=ax^2+c?\end{align*}$   Why or why not?
     ::点数(10,0)和点数(10,0)是否足以确定y=ax2+c形式之四方形的独特方程式?为什么或为什么不?

  播放段落

  Interactive
  ::交互式互动

  播放段落

  In the interactive below, move the red and blue points to explore the conditions under which two quadratics of the form $\begin{align*}f(x)=ax^2+c \end{align*}$  intersect in no points, one point, or two points. Explain how these results will be evident when solving equations to find the intersection. 
  ::在下文互动部分,移动红点和蓝点以探索 f(x) = ax2+c 窗体的两个四方形在无点、一点或两点中交叉的情况。请解释在解开方程式以找到交叉点时,这些结果将如何显现出来。

  播放段落

    Summary
  ::摘要

  播放段落
  • A quadratic function in standard form with no linear term is also in vertex form.
    ::标准形式的二次函数,无线性术语,也以顶点形式出现。
  播放段落
  • The structure for such a quadratic is $\begin{align*}y=ax^2+c.\end{align*}$
    ::这种二次方体的结构是 y=ax2+c。
  播放段落
  • Given either $\begin{align*}a\end{align*}$  or $\begin{align*}c,\end{align*}$ and a point on the quadratic, the other parameter can be determined.
    ::如果给定一个或 c, 以及二次曲线上的点, 则可以确定其他参数 。
  播放段落
  • Given two points on such a quadratic, both parameters can be determined by solving a linear system.
    ::考虑到这种二次曲线的两点,这两个参数都可以通过解决线性系统来确定。
  播放段落
  • There can be 0,1, or 2 solutions to any quadratic equation.
    ::任何二次方程式都可能有0、1或2个解决方案。