Course: 4.14 平根功能和平方-interactive | The Way To Learn

The Way To Learn

Section outline

Select section General

Collapse Expand
General

Collapse all Expand all
- Select activity 新闻通告
  
  新闻通告 Forum
Select section 平根函数和方根等量

Collapse Expand
平根函数和方根等量
The Purpose of this Lesson
::本课程的目的

In this lesson, you will explore the square root function in the context of inverse relations. You'll graph transformed square root functions and solve .
::在此教训中, 您将在反向关系中探索平方根函数。您将绘制正方根函数的变形图并解决。

Introduction: T he Inverse of the Quadratic F u nction
::导言:Quadratic 函数的反面

Work it Out
::工作出来

Graph the function $\begin{aligned} f (x) = x^{2} . \end{aligned}$ Find the inverse. Solve it for $\begin{aligned} y . \end{aligned}$ Graph it. Graph the line $\begin{aligned} y = x . \end{aligned}$ Compare the inverse of $\begin{aligned} f (x) \end{aligned}$ with the original. What is the domain and range of the original? What is the domain and range of the inverse? What do you observe?
::函数 f( x) =x2 的图解。查找反向。为 y 解决它。绘制线条 y=x 。比较 f( x) 与原始的反义。原始的域和范围是什么? 反向的域和范围是什么? 您观察了什么 ?

Activity 1 : The Square Root Function
::活动1: " 平根功能 "

In the last problem, you saw that the equations $\begin{aligned} y = x^{2} \end{aligned}$ and $\begin{aligned} y = \pm \sqrt{x} \end{aligned}$ are inverse relations.
::在最后一个问题中,你看到 y=x2和y=x是反向关系。

Example 1-1
::例1-1

$\begin{aligned} y = \pm \sqrt{x} \end{aligned}$ is not a function . Why not? $\begin{aligned} y = \sqrt{x} \end{aligned}$ is a function. How do you know? What is its domain and range?
::yx 不是函数。为什么不? y=x是一个函数。你怎么知道? 它的域和范围是什么?

Solution: The graph of $\begin{aligned} y = \pm \sqrt{x} \end{aligned}$ shows us that there is an infinite number of $\begin{aligned} x \end{aligned}$ values that return more than one $\begin{aligned} y \end{aligned}$ value. This doesn't meet our definition of a function. A function is a relation between two sets of numbers, the domain, and range, such that for each $\begin{aligned} x \end{aligned}$ value in the domain there is only one $\begin{aligned} y \end{aligned}$ value in the range. Substituting values for $\begin{aligned} x \end{aligned}$ , or the vertical line test for the graph, show that $\begin{aligned} y = \pm \sqrt{x} \end{aligned}$ does not meet the definition of a function.
::解析度 : yx 的图形向我们显示, 返回一个 y 值的 x 值是无限的。这不符合我们对函数的定义。函数是两组数字之间的关系, 即域和范围, 因此对于域内的每个 x 值来说, 区域里只有一个 y 值。替换 x 的值, 或图形的垂直线测试, 显示 yx 不符合函数的定义。

The equation y = plus or minus the square root of x is not a function, but y = the square root of x is. Why?
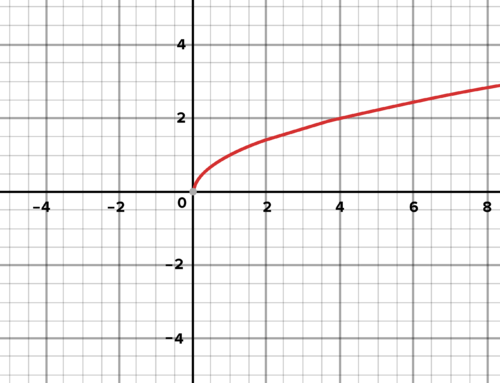
::公式 y = + 或减去 x 的平方根不是函数,而是 y = x 的平方根是。为什么?

By contrast, $\begin{aligned} y = \sqrt{x} \end{aligned}$ is a function. It passes the vertical line test. The domain for $\begin{aligned} y = \sqrt{x} \end{aligned}$ is $\begin{aligned} [0, \infty) . \end{aligned}$ The range is $\begin{aligned} [0, \infty) . \end{aligned}$
::相对而言, Y=x 是一个函数。它通过垂直线测试。y=x 的域为 [0,\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\Y\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\

The equation y = plus or minus the square root of x is not a function, but y = the square root of x is. Why?

Interactive
::交互式互动

We can transform the square root function using the same parameters that we used for quadratic functions. Use the interactive below to investigate how $\begin{aligned} a, \end{aligned}$ $\begin{aligned} h, \end{aligned}$ and $\begin{aligned} k \end{aligned}$ affect the square root function $\begin{aligned} y = \sqrt{x} . \end{aligned}$
::我们可以使用用于二次函数的相同参数来转换平方根函数。使用下面的交互功能来调查a、 h和 k如何影响平方根函数 y=x 。

INTERACTIVE

Transforming Square Root Functions

Move the red, blue, and green points to change the stretch, horizontal, and vertical shifts of the square root function.
::移动红色、蓝色和绿色点以改变平方根函数的伸缩、水平和垂直移动。

Your device seems to be offline.
Please check your internet connection and try again.

+

Do you want to reset the PLIX?

Yes

No

Work it Out
::工作出来

Transform the square root function $\begin{aligned} f (x) = \sqrt{x} \end{aligned}$ according to each set of instructions below. Call the result after each transformation $\begin{aligned} h (x) . \end{aligned}$ Write the equation for each result. Sketch the graph of each. Give the domain and range of each. Based on the graph, state if the equation $\begin{aligned} h (x) = 2 \end{aligned}$ has a solution, and why or why not. Do not solve the equation.
::根函数 f( x) =x 根据以下每组指令进行转换。在每次转换 h( x) 后调出结果。写入每个结果的方程。绘制每个结果的图形。给出每个结果的域和范围。根据图形, 显示公式 h( x) =2 是否有解决方案, 以及为什么或为什么没有。请不要解析方程。

Shift 5 vertically .
::垂直移动 5 。

Shift 3 horizontally .
::水平上移移移 3 。

Shift 5 vertically and 3 horizontally.
::垂直移5和横向移3。

Stretch by a factor of 2.
::伸展乘以 2 乘以 2 。

Shift -3 vertically.
::- 垂直移动 - 垂直移动 - 垂直移动 - Shift - 3 toird - 3 toird

Stretch by a factor of negative 1.
::以负1系数拉伸

Activity 2: Solving Square Root Equations
::活动2:解决平方根等

Example 2-1
::例2-1

In the last problem, there were several cases when the equation $\begin{aligned} h (x) = 2 \end{aligned}$ did not have a solution. The example below shows the process for solving equations with square roots. Although this process will always result in a numerical answer, the answer is not always a valid solution to the equation.
::在最后一个问题中,有几种情况是公式h(x)=2没有解决办法。下面的例子显示了用正方根解析方程式的过程。虽然这一过程总是得出数字答案,但答案并不总是对等方程式有效的解决办法。

$\begin{aligned} \begin{array}{ll} Equation & Explanation \\ - 3 \sqrt{x - 2} + 7 = 19 & Given equation. \\ - 3 \sqrt{x - 2} = 12 & Subtracting. \\ \sqrt{x - 2} = - 4 & Dividing. \\ x - 2 = 16 & Squaring both sides. (Squaring is the inverse of square rooting.) \\ x = 18 & Adding. \\ - 3 \sqrt{18 - 2} + 7 = 19 & Checking answer by substituting to see if it's a solution. \\ - 3 \sqrt{16} + 7 = 19 \\ - 3 (4) + 7 = 19 \\ - 12 + 7 = 19 \\ - 5 = 19 & This statement is false. 18 is not a solution. There is no solution. \end{array} \end{aligned}$

::EquationExplantation- 3x-2+7=19 给定方程式。- 3x-2=12 减序. x-24Dividide.x-2=16S 双方对齐。 (对齐是平方根的反方。)x=18Add.-318-2+7=19 通过替换检查答案,看它是否是一个解决方案。- 316+7=19-3(4)=19- 12+7=19-5=19=19 本语句是虚假的。 18 不是一个解决方案, 没有解决方案。

Graphing $\begin{aligned} y = - 3 \sqrt{x - 2} + 7 and y = 19 \end{aligned}$ shows no intersection , which means the equation $\begin{aligned} - 3 \sqrt{x - 2} + 7 = 19 \end{aligned}$ has no solution. Look at the transition from the third to the fourth line above. At that step, negative 4 was squared. This introduced an extraneous solution . An extraneous solution is a solution that is not valid.
::图形 y3x-2+7 和 y=19 显示没有交叉点, 这意味着方程式 3x-2+7=19 没有解决方案。看看上面第三行向第四行的过渡情况。在此步骤中, 负 4 平方。这引入了一个不相干解决方案。一个不相干解决方案是无效的解决方案。

Work it Out
::工作出来

Below are several square root equations. Solve each by isolating the expression involving a square root, then squaring both sides to finish solving. Substitute each answer in the original equation to check if it is actually a solution. In the cases where the answer was not a solution, explain the absence of a solution by graphing the function on the left side of the equation.
::下面是几个平方根方程式。通过分离涉及平方根的表达式来解决每一个问题, 然后将双方隔开以完成解答。在原始方程式中替换每个答案以检查它是否真正是一个解决方案。在答案不是解决方案的情况下, 请用方程式左侧的图解来解释没有解决方案。

$\begin{aligned} \begin{array}{ll} a. & \sqrt{x} = - 5 \\ b. & \sqrt{a} + 7 = 1 \\ c. & - \sqrt{x} = 4 \\ d. & - 2 \sqrt{x} = 6 \\ e. & 3 \sqrt{x} = 12 \\ f. & \sqrt{x - 4} = 5 \\ g. & \sqrt{x + 1} + 4 = 5 \\ h. & 3 \sqrt{x - 1} + 5 = 7 \\ i. & \sqrt{x + 4} = 0 \end{array} \end{aligned}$
::a.xxxxxxxxxxx+4=5h.3x-1+5=7i.x+4=0

Solving Equations Involving Square Roots
::涉及 " 平根 " 的溶解平方

Isolate the expression involving the square root.
::分离涉及平方根的表达式。

Square both sides, then continue solving.
::双方平方,然后继续解决。

Check for extraneous solutions by substituting your answer into the original equation.
::将答案替换为原始方程, 以检查不相干的解决办法。

Solve each of the following equations by isolating the expression involving a square root, then squaring both sides to finish solving. Check for extraneous solutions by substituting.
::通过分离涉及平方根的表达式来解析以下方程式中的每一个方程式, 然后将双方隔开以完成解析。通过替换来检查不相干的解决办法。

$\begin{aligned} \begin{array}{ll} a. & \sqrt{x} = x \\ b. & \sqrt{x} = x + 1 \\ c. & \sqrt{x} = x - 1 \\ d. & \sqrt{x} = - x \\ e. & \sqrt{x} = 2 x \\ f. & \sqrt{x - 1} = x \end{array} \end{aligned}$
::ax=xb.x=x+1c.x=x-1d.x=xxxxx=2xf.x-1=x

A traditional sailboat can increase its top speed by increasing its length. But the top speed is not directly proportional to its length. In other words, speed is not a linear function of length. The top speed is also not directly proportional to the square of its length. In other words, speed is not a quadratic function of length. The top speed of a sailboat is directly proportional to the square root of its length. Here is the equation approximately relating the top speed of a sailboat in kilometers per hour to its length in meters:
::传统的帆船可以通过增加长度来增加其顶部速度。但顶部速度与其长度不直接成正比。换句话说, 速度不是长度的线性函数。顶部速度也与其长度的正方形不直接成正比。换句话说, 速度不是长方形函数。帆船的顶部速度与其长度的平方根直接成正比。这里的方程式大约是每小时以公里计的帆船顶部速度与长度的米数:

$\begin{aligned} s (x) = 1.4 \sqrt{x} \end{aligned}$

::s(x)=1.4x

Graph this function. Find the top speeds for boats of different lengths. Find the length required for a desired top speed. If the boat length is increased from 3 meters to 12 meters, by what factor does the speed increase? (Hint: divide $\begin{aligned} s (12) \end{aligned}$ by $\begin{aligned} s (3) .) \end{aligned}$ In general, if the length is quadrupled from $\begin{aligned} a \end{aligned}$ to $\begin{aligned} 4 a, \end{aligned}$ by what factor does the speed increase?
::图形显示此函数。查找不同长度船只的最高速度。查找需要的最高速度所需的长度。如果船的长度从3米增加到12米, 速度会增加什么因素? (提示: 将 s( 12) 除以 s(3) 。) 一般来说, 如果长度从一到 4a 翻四番, 速度会增加什么因素?

Summary
::摘要

If two linear functions are inverses, $\begin{aligned} f (g (x)) = x and g (f (x)) = x . \end{aligned}$
::如果两个线性函数为反函数, f( g( x))=x 和 g( f( x))=x。

An inverse relation for any relation can be created by exchanging $\begin{aligned} x \end{aligned}$ and $\begin{aligned} y . \end{aligned}$
::任何关系的反比关系可以通过交换 x 和 y 来建立。

$\begin{aligned} y = x^{2} and y = \pm \sqrt{x} \end{aligned}$ are inverse relations.
::y=x2和yx是反向关系。

$\begin{aligned} y = \pm \sqrt{x} \end{aligned}$ is not a function.
::yx 不是一个函数。

Square root functions can be solved by isolating the root and squaring both sides. Check for extraneous solutions.
::平方根函数可以通过分离根和分隔两侧来解决。检查不相干的解决办法。

版权所有 © 2024 由瓜瓜科技thewaytolearn.cn设计。保留所有权利。