4.4 关于三角的理论-interactive

Section outline

• Select section General

  Collapse Expand

  General

  Collapse all Expand all

  • Select activity 新闻通告

    

    新闻通告 Forum
• Select section 关于三角的定理

  Collapse Expand

  关于三角的定理

  Recall that a triangle is a shape with exactly three sides. Triangles can be classified by their sides and by their angles .

  播放段落

  When classifying a triangle by its sides, you should look to see if any of the sides are the same length.
  ::三角形的侧面分类时,你应该看看其中一方的长度是否相同。

  播放段落
  • If no sides are the same length, then it is a scalene triangle .
    ::如果没有两边的长度相同,那它就是一个缩放三角形。
  播放段落
  • If two sides are the same length, then it is an isosceles triangle .
    ::如果两边长度相同,则是一个等分形三角形。
  播放段落
  • If all three sides are the same length, then it is an equilateral triangle .
    ::如果所有三边的长度相同,那么它就是一个等边三角。

  播放段落

  When classifying a triangle by its angles, you should look at the size of the angles:
  ::按角度对三角形进行分类时, 您应该查看角的大小 :

  播放段落
  • If  a triangle  has a right angle , then it is a right triangle .
    ::如果三角形有右角,则右角为右角。
  播放段落
  • If the measures of all angles in a triangle are less than $\begin{array}{r}{90}^{\circ }\end{array}$ , then it is an acute triangle .
    播放段落
    • A special case of an acute triangle is when all three angles are equal. In  that case, all three angles  are 60 degrees, and  they form  an equiangular triangle .
      ::急性三角形的特殊情况是所有三个角度都相等。在这种情况下,所有三个角度都为60度,它们形成一个等角三角形。
    
    ::如果三角形中所有角度的度量小于 90 ,则它是一个急性三角形。 急性三角形的一个特例是所有三个角度都相等时。 在这种情况下, 所有三个角度都是60 度, 它们组成一个等角三角形 。
  播放段落
  • If the measure of one angle in a triangle is greater than $\begin{array}{r}{90}^{\circ }\end{array}$ , then it is an obtuse triangle .
    ::如果三角形中一个角度的度量大于 90 ,则该角是一个隐形三角形。

  ---

  播放段落

  Triangle Sum Theorem
  ::三角三角间苏门神话

  播放段落

  Prove that the interior angles of a triangle  sum to   $\begin{array}{r}{180}^{\circ }.\end{array}$
  ::证明三角形和180的内角。

  播放段落

  This is a property of triangles that you have heard of and used before, but you may not have ever seen a proof for why it is true. Here is a paragraph format proof that relies on parallel lines and .
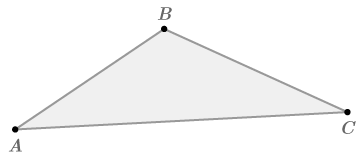
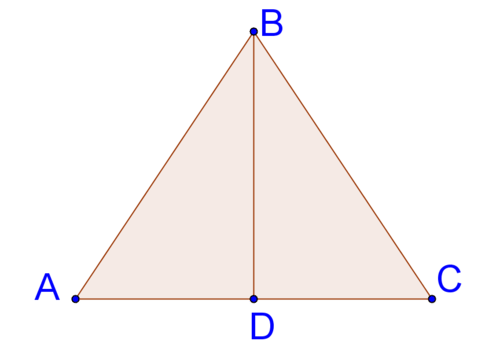
  ::这是您以前听说过并使用的三角形属性, 但您可能从未看到过它为何属实的证据 。 这是段落格式的证明, 依赖于平行的线条和 。

  播放段落

  Consider the generic triangle below.
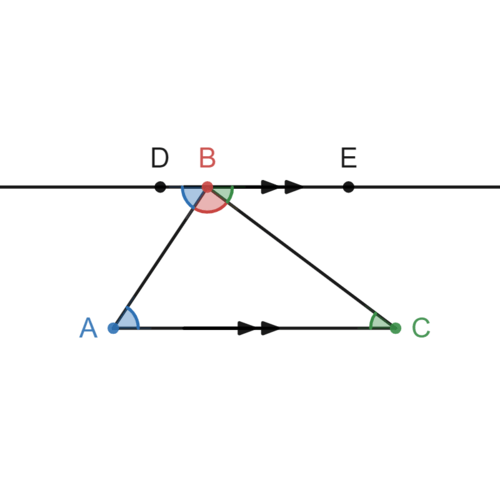
  ::考虑下面的通用三角形。

  

  播放段落

  By the parallel postulate , there exists exactly one line parallel to $\begin{array}{r}\overline{AC}\end{array}$ through $\begin{array}{r}B\end{array}$ . Draw this line.
  ::在平行假设中, 完全有一条线与 AC 平行, 通过 B 。 绘制这条线 。

  播放段落

    $\begin{array}{r}\mathrm{\angle }DBA\cong \mathrm{\angle }A\end{array}$ because they are alternate interior angles and alternate interior angles are congruent when lines are parallel. Therefore, $\begin{array}{r}m\mathrm{\angle }DBA=m\mathrm{\angle }A\end{array}$ . Similarly, $\begin{array}{r}\mathrm{\angle }EBC\cong \mathrm{\angle }C\end{array}$ because they are also alternate interior angles, and so $\begin{array}{r}m\mathrm{\angle }EBC=m\mathrm{\angle }C\end{array}$ . $\begin{array}{r}m\mathrm{\angle }DBA+m\mathrm{\angle }ABC+m\mathrm{\angle }EBC={180}^{\circ }\end{array}$ because these three angles form a straight line. By substitution, $\begin{array}{r}m\mathrm{\angle }A+m\mathrm{\angle }ABC+m\mathrm{\angle }C={180}^{\circ }\end{array}$ .
  ::DBAA 因为它们是不同的内部角度, 而其它的内部角度在线条平行时是相似的。 因此, mDBA=mA。 同样, EBCC 因为它们也是不同的内部角度, 所以 mEBC=mC. mDBA+mABC+mBC=180, 因为这三个角度组成一条直线。 替换为 mA+mABC+mC=180。

  播放段落

  The statement " the sum of the measures of the interior angles of a triangle is $\begin{array}{r}{180}^{\circ }\end{array}$ " is known as the Triangle Sum Theorem . Now that it has been proven, you can use it in future proofs without proving it again.
  ::语句“ 三角形Is180的内部角度测量总和” 被称为三角形 Sum 理论。 既然已经证明了这一点, 您可以在未来的证明中使用它, 而不再次证明它 。

  播放段落

  Click the small blue arrow next to the image below and then drag the orange vertices to reshape the triangle. Observe that the sum of the measures of the interior angles of a triangle is always $\begin{array}{r}{180}^{\circ }\end{array}$ .
  ::单击下方图像旁边的小蓝箭头,然后拖动橙色顶部以重塑三角形。观察三角形内角的测量总和总是 180 。

  ---

  播放段落

  Isosceles Triangle Theorem
  ::Isosceles 三角三角定理

  播放段落

  Prove that the base angles of an isosceles triangle are congruent.
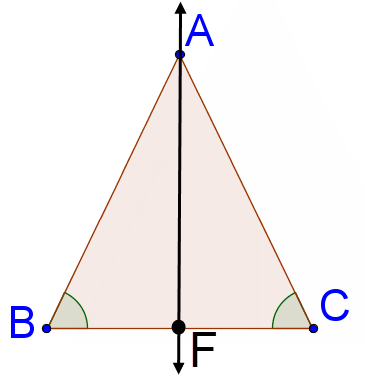
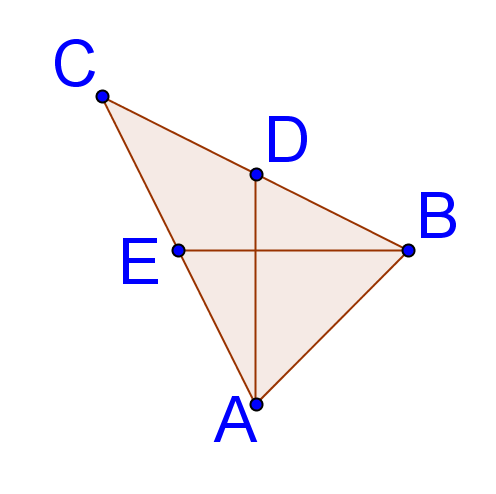
  ::证明一个等分形三角形的基角是相容的。

  播放段落

  The base angles of an isosceles triangle are the angles opposite the congruent sides . Below, the base angles are marked for isosceles $\begin{array}{r}\mathrm{△}ABC\end{array}$ .
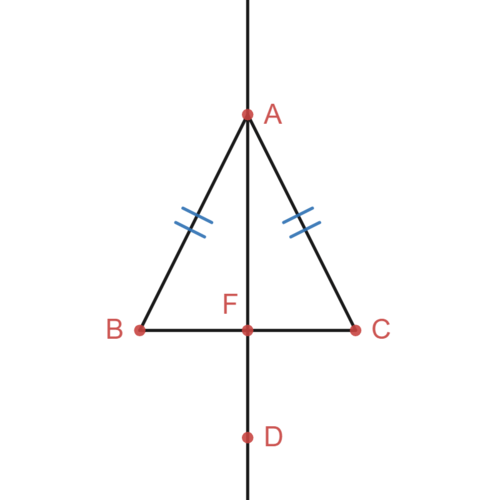
  ::等分形三角形的基角是相近边对面的角。以下为等分形 ABC 标记基角。

  播放段落

  You need to prove that $\begin{array}{r}\mathrm{\angle }B\cong \mathrm{\angle }C\end{array}$ given that $\begin{array}{r}\overline{AB}\cong \overline{AC}\end{array}$ . Here is a proof in the two-column format, that relies on angle bisectors and . The proof will reference the picture below.
  ::您需要证明 AB AC 。 这是两列格式的证明, 依赖于角度的分区和 。 证明将引用下面的图片 。

  播放段落 Statements ::声明声明 声明 声明 声明 声明 声明 声明 声明 声明 声明 声明 声明 声明 声明 声明 声明 声明 声明 声明 声明	播放段落 Reasons ::原因原因原因原因
  播放段落 Isosceles $\begin{array}{r}\mathrm{△}ABC\end{array}$ ::Isosceles ABC	播放段落 Given ::给
  $\begin{array}{r}\overline{AB}\cong \overline{AC}\end{array}$	播放段落 Definition of isosceles triangle ::Isosceles 三角形定义
  播放段落 Construct $\begin{array}{r}\stackrel{\leftrightarrow }{AD}\end{array}$ , the angle bisector of $\begin{array}{r}\mathrm{\angle }A\end{array}$ , with $\begin{array}{r}F\end{array}$ the intersection of $\begin{array}{r}\overline{BC}\end{array}$ and $\begin{array}{r}\stackrel{\leftrightarrow }{AD}\end{array}$ ::建构 AD, A的角, 与 F 相交的 BC' 和 AD	播放段落 An angle has only one angle bisector ::一个角度只有一个角度的分角
  $\begin{array}{r}\overline{AF}\cong \overline{AF}\end{array}$	播放段落 Reflexive Property ::弹性财产
  $\begin{array}{r}\mathrm{\angle }BAF\cong \mathrm{\angle }CAF\end{array}$	播放段落 Definition of angle bisector ::角度分部门的定义
  播放段落 $\begin{array}{r}\mathrm{△}ABF\cong \mathrm{△}ACF\end{array}$ ::ACF	播放段落 $\begin{array}{r}SAS\cong \end{array}$ ::SAS_______________________________________________________________________________________________________________________________________________________________________________________________
  $\begin{array}{r}\mathrm{\angle }B\cong \mathrm{\angle }C\end{array}$

  播放段落

  The statement " the base angles of an isosceles triangle are congruent " is  the Isosceles Triangle  Theorem . Now that it has been proven, you can use it in future proofs without proving it again.
  ::语句“ 等分形三角形的基本角度是相容的” 是“ 等分形三角形理论” 。 现在, 它已被证实, 您可以在未来的证明中使用它, 而不再次证明它 。

  播放段落

  Click the small blue arrow next to the image below and then drag the orange vertices to reshape the triangle. Observe that the base angles of an isosceles triangle are always congruent.
  ::单击下方图像旁边的蓝色小箭头,然后拖动橙色的脊椎重塑三角形。注意一个等分形三角形的基角度总是相似的。

  ---

  播放段落

  Exterior Angles Theorem
  ::外部外角定理

  播放段落

  Prove that the measure of an exterior angle of a triangle is equal to the sum of the measures of the remote interior angles .
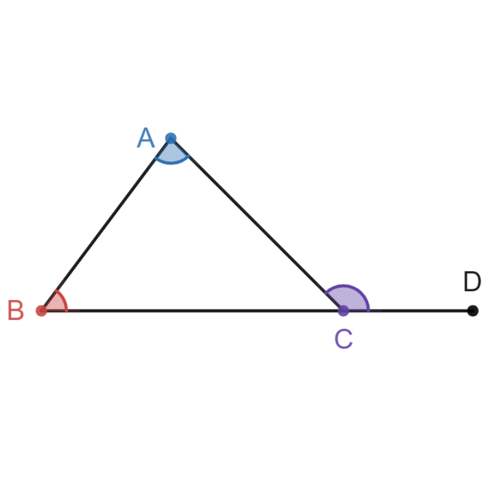
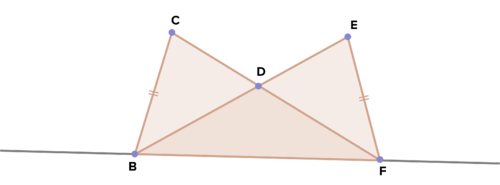
  ::证明三角形外角的度量等于边远内角的度量总和。

  播放段落

  An exterior angle of a triangle is an angle outside of a triangle created by extending one of the sides of the triangles. Below, $\begin{array}{r}\mathrm{\angle }ACD\end{array}$ is an exterior angle . For exterior angle $\begin{array}{r}\mathrm{\angle }ACD\end{array}$ , the angles $\begin{array}{r}\mathrm{\angle }A\end{array}$ and $\begin{array}{r}\mathrm{\angle }B\end{array}$ are the remote interior angles , because they are the interior angles that are not adjacent to the exterior angle.
  ::三角形的外角是一个三角形外角,它是一个三角形外角外角。下面, QACD 是一个外角。 对于外部角 QACD , 角 QACD 和 QB 是边远的内角, 因为它们是与外角不相邻的内角 。

  播放段落

  Here is a flow diagram proof of this theorem.
  ::这是这个理论的流程图证明。

  

  播放段落

  The statement "the measure of an exterior angle of a triangle is equal to the sum of the measures of the remote interior angles " is the  Exterior Angles Theorem . Now that it has been proven, you can use it in future proofs without proving it again.
  ::语句“三角形外角的度量等于边远内角的度量总和”是“外角定理”。既然已经证明了这一点,您可以在今后的证明中使用它,而不必再次证明。

  播放段落

  Click the small blue arrow next to the image below and then drag the orange vertices to reshape the triangle. Choose two remote interior angles of the triangle and observe how measure of an exterior angle remains equal to the sum of the remote interior angles.
  ::单击下方图像旁边的蓝色小箭头,然后拖动橙色的顶部以重塑三角形。选择三角形的两个偏远内部角度,观察外部角度的测量与远程内部角度的和等值。

  播放段落

  A & B
  ::A和B

  播放段落

  In the interactive below, move the red points to change the shape of the triangle. Move the blue points to compare angles $\begin{array}{r}\mathrm{\angle }1,\mathrm{\angle }2,\end{array}$ and $\begin{array}{r}\mathrm{\angle }3.\end{array}$
  ::在下面交互的交互点中,移动红色点以改变三角形的形状。移动蓝色点以比较角++1,%2,和++3。

  播放段落

  Notice that because they are , the angle pairs $\begin{array}{r}m\mathrm{\angle }1=m\mathrm{\angle }4,m\mathrm{\angle }2=m\mathrm{\angle }5,\end{array}$ and $\begin{array}{r}m\mathrm{\angle }3=m\mathrm{\angle }6.\end{array}$
  ::注意,因为是, 角度对应 m1 = m4, m2 = m5, 和 m3 = m6。

  播放段落

  $$\begin{array}{rl}m\mathrm{\angle }1+m\mathrm{\angle }2+m\mathrm{\angle }3& ={360}^{\circ }\\ m\mathrm{\angle }4+m\mathrm{\angle }5+m\mathrm{\angle }6& ={360}^{\circ }\end{array}$$

  
  ::@ m1+m%2+m%3=360 @m @4+m @5+m#6=360 @

   

  ---

  播放段落

  Triangle Midsegment Theorem
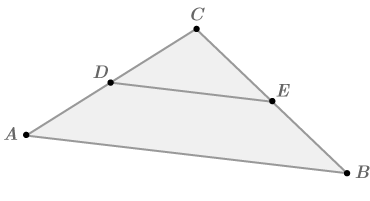
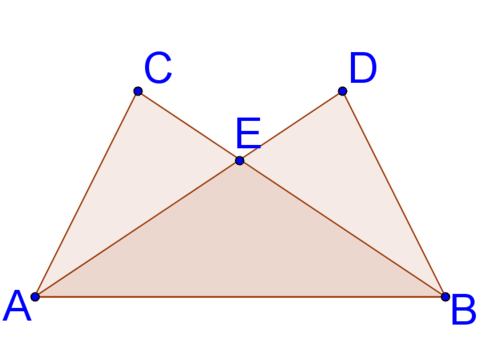
  ::三角三角区中分定理

  播放段落

  In the triangle below, point $\begin{array}{r}D\end{array}$ is a midpoint of $\begin{array}{r}\overline{AC}\end{array}$ and point $\begin{array}{r}E\end{array}$ is the midpoint of $\begin{array}{r}\overline{BC}\end{array}$ . Make a conjecture about how $\begin{array}{r}\overline{DE}\end{array}$ relates to $\begin{array}{r}\overline{AB}\end{array}$ .
  ::D点是AC的中点,E点是BC的中点。

  

  播放段落

  A conjecture is a guess about something that might be true. After making a conjecture, usually you will try to prove it. Two possible conjectures are:
  ::猜想是对的猜测。在作出猜想之后,通常你会试图证明这一点。两种可能的猜想是:

  播放段落
  1. $\begin{array}{r}\overline{DE}\Vert \overline{AB}\end{array}$
     ::阿B
  播放段落
  2. The length of $\begin{array}{r}\overline{DE}\end{array}$ is half the length of $\begin{array}{r}\overline{AB}\end{array}$
     ::DE的长度是AB的长度的一半

  播放段落

  Consider the picture below.
  ::考虑以下情况。

  播放段落

  To prove the conjecture $\begin{array}{r}DE\parallel AB\end{array}$ , we need to prove that $\begin{array}{r}\mathrm{△}FEB\cong \mathrm{△}DEC\end{array}$ which we then use to prove that $\begin{array}{r}BF\parallel AC\end{array}$ . We then continue with the proof to prove that $\begin{array}{r}\mathrm{△}ADB\cong \mathrm{△}FBD\end{array}$ which then leads us to prove that $\begin{array}{r}DE\parallel AB\end{array}$ .
  ::为了证明 DE AB 的推测,我们需要证明 我们用来证明 BF AC 的“FEB DEC ” 。 然后我们继续证明 AB 的“ADB ” , 从而证明 DEAB 。

  	播放段落 Statements ::声明声明 声明 声明 声明 声明 声明 声明 声明 声明 声明 声明 声明 声明 声明 声明 声明 声明 声明 声明 声明	播放段落 Reasons ::原因原因原因原因
  1.	$\begin{array}{r}\overline{DC}\cong \overline{AD}\end{array}$ , $\begin{array}{r}\overline{CE}\cong \overline{EB}\end{array}$ , $\begin{array}{r}\overline{DE}\cong \overline{EF}\end{array}$	播放段落 Given ::给
  	$\begin{array}{r}\mathrm{\angle }CED\cong \mathrm{\angle }FEB\end{array}$	播放段落 Vertical angles are congruent ::垂直角度是相似的
  	$\begin{array}{r}\mathrm{△}FEB\cong \mathrm{△}DEC\end{array}$	$\begin{array}{r}SAS\cong \end{array}$
  2.	$\begin{array}{r}\mathrm{\angle }FBE\cong \mathrm{\angle }ECD\end{array}$	播放段落 CPCTC ::方案协调会
  	$\begin{array}{r}\overline{BF}\Vert \overline{AC}\end{array}$	播放段落 If alternate interior angles are congruent then lines are parallel. ::如果其它内部角度相同,则线条平行。
  3.	$\begin{array}{r}\mathrm{\angle }ADB\cong \mathrm{\angle }DBF\end{array}$	播放段落 If lines are parallel then alternate interior angles are congruent. ::如果线条是平行的,则不同的内部角度是相似的。
  	$\begin{array}{r}\overline{DB}\cong \overline{DB}\end{array}$	播放段落 Reflexive property ::弹性财产
  	$\begin{array}{r}\overline{BF}\cong \overline{DC}\end{array}$	播放段落 CPCTC ::方案协调会
  	$\begin{array}{r}\overline{BF}\cong \overline{AD}\end{array}$	播放段落 Substitution ::替代替代
  	$\begin{array}{r}\mathrm{△}ADB\cong \mathrm{△}FBD\end{array}$	$\begin{array}{r}SAS\cong \end{array}$
  4.	$\begin{array}{r}\mathrm{\angle }ABD\cong \mathrm{\angle }FDB\end{array}$	播放段落 CPCTC ::方案协调会
  	$\begin{array}{r}\overline{DE}\Vert \overline{AB}\end{array}$	播放段落 If alternate interior angles are congruent then lines are parallel. ::如果其它内部角度相同,则线条平行。

  播放段落

  Here is  the figure again, for reference:
  ::以下是图一,供参考:

  播放段落

  Now prove the conjecture that the length of $\begin{array}{r}DE\end{array}$ is half the length of $\begin{array}{r}AB.\end{array}$
  ::现在证明假设DE的长度是AB的长度的一半。

  	Statements	Reasons
  5.	$\begin{array}{r}\overline{DF}\parallel \overline{AB}\end{array}$	$\begin{array}{r}\overline{DE}\end{array}$ produced at $\begin{array}{r}F\end{array}$
  	$\begin{array}{r}\overline{BF}\parallel \overline{AD}\end{array}$	$\begin{array}{r}D\end{array}$ is a midpoint of $\begin{array}{r}AC\end{array}$
  	$\begin{array}{r}ABFD\end{array}$ is a	Definition of a parallelogram
  	$\begin{array}{r}\overline{DE}=\frac{1}{2}\overline{DF}\end{array}$	$\begin{array}{r}\overline{DE}\cong \overline{EF}\end{array}$
  	$\begin{array}{r}\overline{DE}=\frac{1}{2}\overline{AB}\end{array}$	Definition of a parallelogram

  播放段落

  Thus, the line segment joining the midpoints of any two sides of a triangles is parallel to the third side and equal to half of it, this is the Triangle Midsegment Theorem . Note that there are other ways to prove that the two segments are parallel. One method relies on similar triangles , which will be explored in another concept.
  ::因此,连接三角形任何两边中点的线段与三角形第三侧平行,等于一半,这就是三角区段定理。请注意,还有其他方法可以证明这两个区段是平行的。一种方法依靠类似的三角形,另一个概念将探讨这些三角形。

  播放段落

  Click on the small blue arrow next to the image below and then drag the orange vertices to reshape the triangle. Observe that the line segment joining the mid-points of the two sides of a triangle is parallel to the third side and equal to half of it.
  ::单击下方图像旁边的蓝色小箭头,然后拖动橙色的顶部以重塑三角形。请注意,连接三角形两侧中间点的线段与三角形第三面平行,等于半边。

  ---

  播放段落

  CK-12 PLIX Interactive
  ::CK-12 PLIX 交互式互动

  Summary

  播放段落 If no sides are the same length, then it is a scalene triangle . ::如果没有两边的长度相同,那它就是一个缩放三角形。 播放段落 If two sides are the same length, then it is an isosceles triangle . ::如果两边长度相同,则是一个等分形三角形。 播放段落 If all three sides are the same length, then it is an equilateral triangle . ::如果所有三边的长度相同,那么它就是一个等边三角。 播放段落 If a triangle has a right angle, then it is a right triangle . ::如果三角形有右角,则右角为右角。 播放段落 If the measures of all angles in a triangle are less than 90 o , then it is an acute triangle. ::如果三角形中所有角度的度量小于90o,则是一个急性三角形。 播放段落 If the measure of one angle in a triangle is greater than 90 o , then it is an obtuse triangle. ::如果三角形中一个角度的度量大于90o,则该角度是一个隐形三角形。

  ---

  播放段落

  Review
  ::审查审查审查审查

  播放段落

  1.  Earlier, you proved that the sum of the interior angles of a triangle is $\begin{array}{r}{180}^{\circ }\end{array}$ (the triangle sum theorem) using a paragraph proof. Now, rewrite this proof in the two-column format. Use the following image to help identify points, lines and angles for your proof.
  ::1. 早些时候,您证明三角形内部角的总和是 180 (三角形和定理) , 使用段落证明。 现在, 请用双栏格式重写此证明。 使用以下图像来帮助识别您证明的点、 线条和角度 。

  

  播放段落

  2. Rewrite the proof  of the Triangle Sum Theorem again, this time in the flow diagram format.
  ::2. 再次重写三角SumTheorem的证明,这次以流程图格式重写。

  播放段落

  3.  Earlier, you proved that the base angles of an isosceles triangle are congruent using a two-column proof. Now, rewrite this proof in the paragraph format. Use the following image to help identify points, lines and angles for your proof.
  ::3. 早些时候,您用双栏证明来证明一等分三角形的基角度是相同的。 现在, 请在段落格式中重写此证明。 使用以下图像来帮助识别您证明的点、 线条和角度 。

  

  播放段落

  4. Rewrite the  isosceles triangle theorem  again, this time in the flow diagram format.
  ::4. 再次重写等分形三角定理,这次以流程图格式重写。

  播放段落

  5.  Earlier, you proved that the measure of an exterior angle of a triangle is equal to the sum of the measures of the remote interior angles using the flow diagram format. Now, rewrite this proof in the paragraph format. Use the following image to help identify points, lines and angles for your proof.
  ::5. 早些时候,您证明三角形外部角的测量等于使用流程图格式测量偏远内部角的测量总和。现在,在段落格式中重写此证明。使用以下图像帮助识别用于证明的点、线和角度。

  

  播放段落

  6. Rewrite the exterior angles proof again, this time in the two-column format.
  ::6. 再次重写外部角度证明,这次以两栏格式重写。

  播放段落

  7. Recall that the segment joining midpoints of two sides of a triangle is parallel to the third side of the triangle. Given the diagram below and that $\begin{array}{r}\mathrm{△}ADB\cong \mathrm{△}FBD\end{array}$ as proved earlier in the lesson, prove that $\begin{array}{r}DE=\frac{1}{2}AB\end{array}$ .
  ::7. 回顾三角形两侧的中点相连接的线段与三角形第三侧平行,根据下图和上文的教训所证明的ZADBZ=FBD,证明DE=12AB。

  

  播放段落

  8.  What is the converse of: "If a triangle is isosceles, then the two base angles are congruent".  Why do you think the converse is also true or is not true?
  ::8. " 如果三角形是等分形,那么两个基角度是相容的 " 的反义词是什么?为什么你认为反义词是真实的还是不真实的?

  播放段落

  9. Prove that if two angles of a triangle are congruent, then the triangle is isosceles. Use the diagram and two-column proof below and fill in the blanks to complete the proof.
  ::9. 证明如果三角形的两个角度是相容的,则三角形是等分形。使用下方的图表和两栏证明,填入空白以填充证据。

  

  播放段落 Statements ::声明声明 声明 声明 声明 声明 声明 声明 声明 声明 声明 声明 声明 声明 声明 声明 声明 声明 声明 声明 声明	播放段落 Reasons ::原因原因原因原因
  $\begin{array}{r}\mathrm{\angle }B\cong \mathrm{\angle }C\end{array}$	________
  播放段落 Construct $\begin{array}{r}\stackrel{\leftrightarrow }{AF}\end{array}$ , the angle bisector of $\begin{array}{r}\mathrm{\angle }A\end{array}$ , with $\begin{array}{r}F\end{array}$ the intersection of $\begin{array}{r}\overline{BC}\end{array}$ and $\begin{array}{r}\stackrel{\leftrightarrow }{AF}\end{array}$ ::建构 AF, 角角角 AA, 和FF 交叉点 BC'and AF	播放段落 An angle has only one angle bisector ::一个角度只有一个角度的分角
  ________	播放段落 Definition of angle bisector ::角度分部门的定义
  ________	播放段落 Reflexive Property ::弹性财产
  $\begin{array}{r}\mathrm{△}ABF\cong \mathrm{△}ACF\end{array}$	________
  ________	播放段落 CPCTC ::方案协调会

  播放段落

  10. Rewrite the proof  that a triangle with two congruent angles is isosceles  in the flow diagram format.
  ::10. 重写具有两个相容角度的三角形是流程图格式中的等分形的证据。

  播放段落

  11. Rewrite the isosceles triangle proof in the paragraph format.
  ::11. 在段落格式中重写等分形三角证明。

  播放段落

  12. Given that $\begin{array}{r}\mathrm{△}ABC\cong \mathrm{△}BAD\end{array}$ , prove that $\begin{array}{r}\mathrm{△}AEB\end{array}$ is isosceles.
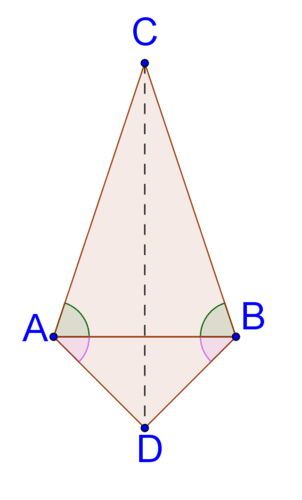
  ::12. 鉴于ABC-BAD,证明AEB是异象。

  

  播放段落

  13. Given the markings in the picture below, explain why $\begin{array}{r}\overline{CD}\end{array}$ is the perpendicular bisector of $\begin{array}{r}\overline{AB}\end{array}$ with a paragraph proof.
  ::13. 鉴于以下图象中的标记,请解释为什么CD's是AB ' 的直角两侧部分,并附有一段证据。

  

  播放段落

  14. In the picture below, $\begin{array}{r}\mathrm{△}ABC\end{array}$ is isosceles with $\begin{array}{r}\overline{AC}\cong \overline{CB}\end{array}$ . $\begin{array}{r}E\end{array}$ is the midpoint of $\begin{array}{r}\overline{AC}\end{array}$ and $\begin{array}{r}D\end{array}$ is the midpoint of $\begin{array}{r}\overline{CB}\end{array}$ . Prove that $\begin{array}{r}\mathrm{△}EAB\cong \mathrm{△}DBA\end{array}$ .
  ::14. 如下图所示,“ABC”是AC =CB 的等距。“E”是AC 的中点,“D”是CB 的中点。

  

  播放段落

  15. Explain why knowing that $\begin{array}{r}\mathrm{△}ABC\end{array}$ is isosceles is not enough information to prove that $\begin{array}{r}\mathrm{△}ABD\cong \mathrm{△}CBD\end{array}$ .
  ::15. 解释为什么知道ABC是隔离状态不足以证明ZABD&CBD。

  

  播放段落

  16 Given: $\begin{array}{r}\mathrm{\angle }CBD\cong \mathrm{\angle }EFD\end{array}$ ; $\begin{array}{r}\overline{CB}\cong \overline{EF}\end{array}$  
  ::16岁 16岁 16岁 16岁 16岁 16岁 16岁 16岁 16岁 16岁 16岁 16岁 16岁 16岁 16岁 16岁 16岁

  播放段落

  Prove: $\begin{array}{r}\mathrm{\angle }DBF\cong \mathrm{\angle }DFB\end{array}$
  ::证明: DBFDFDFB

  

  播放段落

  17. Given: $\begin{array}{r}\overline{BC}\cong \overline{EF}\end{array}$ ; $\begin{array}{r}\overline{CF}\cong \overline{EB}\end{array}$
  ::17. 鉴于:BC ZEF;CF CEEB

  播放段落

  Prove: $\begin{array}{r}\mathrm{△}BDF\end{array}$ is isosceles
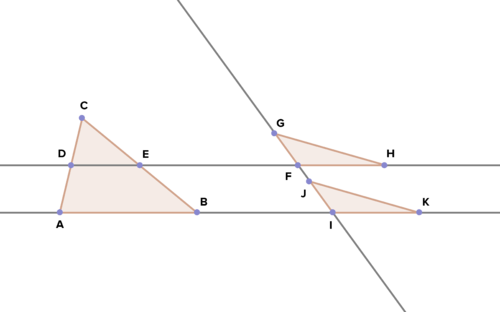
  ::证明: BDF 是等离子体

  

  播放段落

  18. Given: $\begin{array}{r}\overline{DE}\end{array}$ midsegment of $\begin{array}{r}\mathrm{△}ABC\end{array}$ ; $\begin{array}{r}\overline{GF}\cong \overline{JI}\end{array}$ ; $\begin{array}{r}\overline{FH}\cong \overline{IK}\end{array}$
  ::18. 鉴于: ABC的中间部分;GF ji ;FH IK

  播放段落

  Prove: $\begin{array}{r}\mathrm{△}GFH\cong \mathrm{△}JIK\end{array}$
  ::证明:_______________________________________________________________________________________________________________________________________________________________________________________________

  

  播放段落

  Review (Answers) 
  ::审查(答复)

  播放段落

  Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
  ::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键 。