4.6 三角定理的应用-interactive

Section outline

• Select section General

  Collapse Expand

  General

  Collapse all Expand all

  • Select activity 新闻通告

    

    新闻通告 Forum
• Select section 三角定理应用

  Collapse Expand

  三角定理应用

  播放段落

  There are nine theorems related to triangles that are helpful to know.
  ::有九种与三角形相关的定理 有助于了解

  播放段落
  1. Triangle Sum Theorem : The sum of the measures of the interior angles of a triangle is $\begin{align*}180^\circ\end{align*}$ .
     ::三角区 Sumorem : 三角区内部角的测量总和为 180 。
  播放段落
  2. Isosceles Triangle Theorem : The base angles of an isosceles triangle are congruent .
     ::Isosceles三角定理: 等分三角形的基角是相似的 。
  播放段落
  3. Converse of Isosceles Triangle Theorem: If a triangle has two congruent angles then it is isosceles.
     ::与伊索塞尔三角理论相反:如果三角形有两个相近角度,那么就是等索塞尔。
  播放段落
  4. Exterior Angle Theorem: The measure of an exterior angle of a triangle is equal to the sum of the measures of the remote interior angles .
     ::外角定理:三角形外角的测量等于边角内角的测量总和。
  播放段落
  5. Triangle Midsegment Theorem: The segment connecting two midpoints of a triangle is both parallel to and one half the length of the third side of the triangle.
     ::三角形中段理论:连接三角形两个中点的段段,与三角形第三边的长度平行,长度为半。
  播放段落
  6. The three of a triangle meet at the centroid . The centroid divides each median in a 2:1 ratio with the larger segment being the one from the vertex to the centroid.
     
     ::三角形的3个相交于中子机器人。 中子机器人将每个中位数除以2:1的比例, 较大的部分从顶端到中子机器人不等。 三角形的中位数 - CentridRQPG/>Centroid
  播放段落
  7. The three angle bisectors of a triangle meet at the incenter .
     
     ::三角形的三角双角区块在中间点相交。三角形的角双角区块 - IncentFEDIIncenter
  播放段落
  8. The three of a triangle meet at the orthocenter .
     
     ::三角形中的三个在正方形点碰头
  播放段落
  9. The three perpendicular bisectors of a triangle meet at the circumcenter .
     
     ::三角形的3个直角两分区 在环中央汇合

  ---

  播放段落

  CK-12 PLIX Interactive
  ::CK-12 PLIX 交互式互动

  ---

  播放段落

  Examples
  ::实例实例实例实例

  播放段落

  1. Point $\begin{align*}P\end{align*}$ is the centroid of $\begin{align*}\triangle ABC\end{align*}$ . Find the length of $\begin{align*}\overline{AP}\end{align*}$ .
  ::1. P点是ABC的中间体 找出AP的长度

  播放段落

  Because $\begin{align*}P\end{align*}$ is the centroid, it divides each median in a 2:1 ratio , where the length of the segment from the vertex to the centroid is the longer segment. Therefore, we can use this ratio to solve for the length of $\begin{align*}AP\end{align*}$ as follows:
  ::由于P是中子体,它以2:1的比例将每个中位数分隔开来,其中部分的长度从脊椎到中子的长度是较长的部分。因此,我们可以使用这个比例来解决AP的长度问题,具体如下:

  播放段落

  $\begin{align*}\frac{1}{2} & = \frac{PX}{AP} \\ \frac{1}{2} & = \frac{2}{AP}\\ AP & = 2 \cdot 2 = 4 \ \text{in}\end{align*}$
  ::12=PXAP12=2APAP=2

  播放段落

  2. Solve for $\begin{align*}x\end{align*}$ .
  ::2. 解决x.

  

  播放段落

  According to Triangle Sum Theorem, the sum of the measures of the angles is $\begin{align*}180^\circ\end{align*}$ .
  ::根据三角角Sum Theorem, 角度的测量总和是180。

  播放段落

  In $\begin{align*}\triangle ABC\end{align*}$ ,
  ::在ABC,

  播放段落

  $\begin{align*}\angle A + \angle B + \angle C &= 180^\circ \\ (3x-5)+(3x +15)+(2x+2) &=180^\circ\\ 8x+12 &=180^\circ\\ 8x &=168^\circ\\ x &=21^\circ \end{align*}$
  ::ABC=180(3x-5)+(3x+15)+(2x+2)=1808x+12=1808x=168x=21

  播放段落

  3. Prove that two of the medians of an isosceles triangle are congruent.
  ::3. 证明一个等分形三角形的中值中有两个是相容的。

  播放段落

  You can complete this proof using the triangle below. Your goal is to prove that $\begin{align*}\triangle DBC\cong \triangle ECB\end{align*}$ and then show that the medians are congruent because they are corresponding parts of the triangles.
  ::您可以使用下面的三角形来完成此证明。 您的目标是证明 {DBC\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\

  播放段落

  Given: Isosceles $\begin{align*}\triangle ABC\end{align*}$ with medians $\begin{align*}\overline{DC}\end{align*}$ and $\begin{align*}\overline{EB}\end{align*}$ .
  ::以中位数DC和EB为单位。

  播放段落

  Prove: $\begin{align*}\overline{DC} \cong \overline{EB}\end{align*}$
  ::证明:

  播放段落

  Here is a two-column proof:
  ::以下是两栏证明:

  Statement	Reason
  $\begin{align*}\overline{AB} \cong \overline{AC}\end{align*}$	Definition of an isosceles triangle
  $\begin{align*}\overline{AD} \cong \overline{DB} \cong \overline{AE} \cong \overline{EC}\end{align*}$	$\begin{align*}D\end{align*}$ is the midpoint of side $\begin{align*}AB\end{align*}$ and $\begin{align*}E\end{align*}$ is the midpoint of side $\begin{align*}AC\end{align*}$
  $\begin{align*}\angle ABC \cong \angle ACB\end{align*}$	Definition of an isosceles triangle
  $\begin{align*}\overline{BC} \cong \overline{BC}\end{align*}$	Reflexive property
  $\begin{align*}\triangle DBC \cong \triangle ECB\end{align*}$	$\begin{align*}SAS \cong\end{align*}$
  $\begin{align*}\overline{DC} \cong \overline{EB}\end{align*}$	(corresponding parts of are congruent)

  播放段落

  4. Find a place of cardstock or thick paper. Use a ruler and pencil to draw a fairly large random triangle on the paper. Use your ruler to help you construct the centroid of the triangle. Carefully cut out the triangle and try to balance it on the tip of your pencil. Where is the balancing point?
  ::4. 找到卡片或厚纸的地方,使用标尺和铅笔在纸上绘制一个相当大的随机三角形,使用标尺帮助构建三角形的圆形,小心切开三角形,在铅笔的顶端平衡。平衡点在哪里?

  

  播放段落

  You should find that the centroid is the balancing point of the triangle. This means that the centroid is the center of gravity for the triangle when constructed in real life.
  ::您应该发现, 中心机器人是三角形的平衡点。 这意味着当在真实生活中构建时, 中心机器人是三角形的重力中心 。

  播放段落

  5. Point $\begin{align*}P\end{align*}$ is the centroid of $\begin{align*}\triangle ABC\end{align*}$ and $\begin{align*}\overline{BD}=18\end{align*}$ . Find the length of $\begin{align*}\overline{BP}\end{align*}$ .
  ::5. P点是 ABC和BD=18的中间体 找出BP的长度

  播放段落

  The centroid divides the median in a 2:1 ratio where $\begin{align*}\overline{BP}\end{align*}$ is the longer segment.
  ::中央机器人将中位数除以2:1的比例,即BP是较长的区段。

  播放段落

  $\begin{align*}\overline{BP} + \overline{PD} &= \overline{BD} \\ 2x+1x &=18 \\ 3x &= 18 \\ x &= \frac{18}{3} \\ x &=6\\ 2x &=12\end{align*}$
  ::-=============================================================================================================================================================================================================================================================================================================================================================================================================================================================================================================================

  播放段落

  The two segments have lengths of 6 and 12, so $\begin{align*}BP=12\end{align*}$ .
  ::这两个部分的长度分别为6和12,所以BP=12。

  播放段落

  6. Where is the orthocenter of a triangle?
  ::6. 三角形的直角在哪里?

  播放段落

  The three altitudes of a triangle meet at a point called the orthocenter.
  ::三角形的三高度 在一个叫做正弦枢纽的地方相遇

  播放段落

  The altitudes of a triangle are line segments intersecting each vertex and the point on the opposite side where the segment meets the side at a 90-degree angle. In other words, an altitude is a line segment perpendicular to a base and intersecting the opposite vertex.
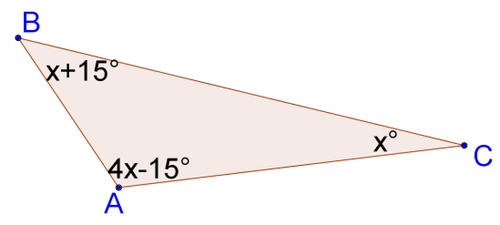
  ::三角形的高度是线条段相交的每个顶部和对面的点,该端段以90度角与侧相交。换句话说,高度是直直直到底部的线段,相互交叉的相反的顶部。

  播放段落

  7. Solve for $\begin{align*}x\end{align*}$ . 
  ::7. 解决x.

    播放段落

  $\begin{align*}\angle BCD\end{align*}$ is the exterior angle of $\begin{align*}\triangle ABC\end{align*}$ at $\begin{align*}C\end{align*}$ and according to exterior angle theorem, the measure of the exterior angle is equal to the sum of the measures of the remote interior angles .
  ::BCD是 C 的 QABC 外角,根据外角理论,外角的测量等于边角内角的测量总和。

  播放段落

  Therefore,
  ::因此,

  播放段落

  $\begin{align*}\angle BCD & = \angle A + \angle B \\ 11x - 15 &= (6x +2) + (4x-2) \\ 11x - 15 & = 10 x \\ 11x - 10x & = 15 \\ x & = 15 \\ \end{align*}$
  ::BCDABB11x-15=(6x+2)+(4x-2)11x-15=10x11-10x=15x=15

  Summary

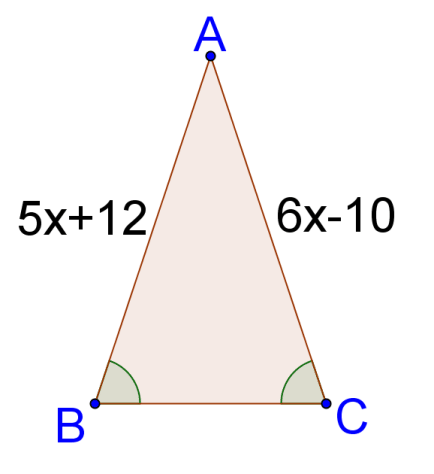
  播放段落 Triangle Sum Theorem: The sum of the measures of the interior angles of a triangle is 180o. ::Sumorem三角形理论:三角形内角的测量总和为180o。 播放段落 Isosceles Triangle Theorem : The base angles of an isosceles triangle are congruent. ::Isosceles三角定理: 等分三角形的基角是相似的 。 播放段落 Exterior Angle Theorem : The measure of an exterior angle of a triangle is equal to the sum of the measures of the remote interior angles. ::外角定理:三角形外角的测量等于边角内角的测量总和。 播放段落 Triangle Midsegment Theorem : The segment connecting two midpoints of a triangle is both parallel to and one half the length of the third side of the triangle. ::三角形中段理论:连接三角形两个中点的段段,与三角形第三边的长度平行,长度为半。 播放段落 Orthocenter : The point of concurrency for the altitudes of triangle.  ::Orthocenter: 三角形高度的货币计算点 。 播放段落 The circumcenter is the point of intersection of the perpendicular bisectors of the sides in a triangle. ::中间点是三角形两侧垂直两侧的交叉点。 播放段落 The incenter is the point where the three angle bisectors of a triangle intersect. ::中间点是三角形的三个角对角相交点。

  ---

  播放段落

  Review
  ::审查审查审查审查

  播放段落

  1. Point $\begin{align*}P\end{align*}$ is the centroid of $\begin{align*}\triangle ABC\end{align*}$ and $\begin{align*}\overline{CD}=12\end{align*}$ . Find the lengths of $\begin{align*}\overline{CP}\end{align*}$ and $\begin{align*}\overline{DP}\end{align*}$ .
  ::1. P点是"ABC"和"CD"的中间体 找出CP和DP的长度

  

  播放段落

  2. A point of concurrency is a point where three lines meet. What are the four points of concurrency in a triangle?
  ::2. 共同货币点是三条线相交点,三角形的四种共同货币点是什么?

  播放段落

  3. The three medians of a triangle meet at a point called the ____________.
  ::3. 三角形的三个中位数在一个称为______的点相交。

  播放段落

  4. The three angle bisectors of a triangle meet at a point called the _____________.
  ::4. 三角形的三个角角对角相交在一个称为____的点上相会。

  播放段落

  5. The three perpendicular bisectors of a triangle meet at a point called the _____________.
  ::5. 三角形的三个直角两侧区块在一个称为______的点相会。

  播放段落

  6. Investigate which points of concurrency are always inside a triangle and which points of concurrency are sometimes outside a triangle (use geometry software to help). What did you find out?
  ::6. 调查哪些同值货币总是在三角内,哪些同值货币有时在三角外(使用几何软件帮助),你发现什么?

  播放段落

  7. Explore the points of concurrency for an equilateral triangle (use geometry software to help). What do you notice?
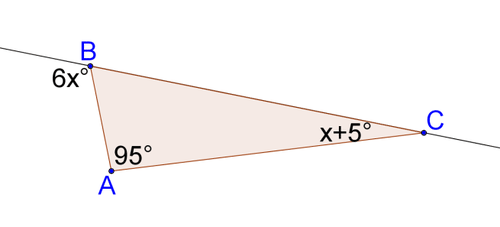
  ::7. 探讨对等三角形(使用几何软件帮助)的共同货币点。你注意到什么?

  播放段落

  Solve for $\begin{align*}x\end{align*}$ .
  ::解决x。

  8.

  

  9.

  

  10.

  

  播放段落

  11. Solve for $\begin{align*}x\end{align*}$ and $\begin{align*}y\end{align*}$ .
  ::11. 解决x和y。

  

  播放段落

  12. Solve for $\begin{align*}x\end{align*}$ .
  ::12. 解决x.

  

  播放段落

  13. In the triangle below,  $\begin{align*}\overline{BC}=x\end{align*}$ , $\begin{align*}\overline{AE}=x-2\end{align*}$ , $\begin{align*}D\end{align*}$ is the midpoint of $\begin{align*}\overline{AB}\end{align*}$ , and $\begin{align*}E\end{align*}$ is the midpoint of $\begin{align*}\overline{AC}\end{align*}$ , and the perimeter of the triangle is 42.
  ::13. 在以下三角形中,`BC 'x, 'AE'=x-2,D是AB的中点,E是AC的中点,三角形的周边是42。

  

  播放段落

  14. Find the lengths of $\begin{align*}\overline{DE}, \overline{AE}\end{align*}$  and $\begin{align*}\overline{AD}\end{align*}$  in the above triangle.
  ::14. 在上述三角形中,找到方形、AE和AE的长度。

  播放段落

  15. A kite has diagonals with lengths 4 and 6. An inner quadrilateral is formed by joining the midpoints of each of the four sides of the kite. What is the perimeter of this inner quadrilateral?
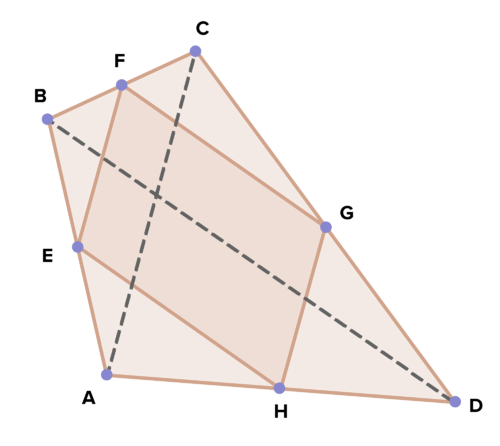
  ::15. 风筝具有4和6长度的对角形,通过将风筝四面每一面的中点结合而形成一个内四边形。

  播放段落

  16. Given: E, F, G, and H are midpoints of their respective sides
  ::16. 鉴于:E、F、G和H是双方的中点

  播放段落

  Prove: EFGH is a parallelogram
  ::证明:EFGH是一个平行图象

  

  播放段落

  17. The centroid is the center of mass of the triangle, its balance point. To balance a metal rod horizontally on one's finger, where is the finger placed? How about the center of mass for a rectangle? How would you locate it? What assumptions are being made about the density of the material of the rectangle? Make some sketches of segments and rectangles, and discuss the calculation of the center of mass for these figures.
  ::17. 圆锥体是三角形质量的中心,它的平衡点。为了横向平衡一根金属棒,手指放在哪里?矩形的质量中心如何?你如何定位它?矩形材料密度的假设是什么?绘制部分和矩形的草图,并讨论这些数字的质量中心计算方法。

  播放段落

  18. Now, c onstruct a triangle in the coordinate plane such that the coordinates of the vertices are integers. This can be constructed by hand or with interactive geometry software . Construct the centroid. Estimate the coordinates of the centroid. Now, calculate the average of x-values of the vertices of the triangle, and the average of the y-values. What do you observe? Why is this the case?
  ::18. 现在,在坐标平面上构造三角形,使顶部的坐标为整数,可以通过手动或互动几何软件构造。 构造中子。 估计中子的坐标。 现在, 计算出三角形顶部的 X 值平均值, 和 Y 值的平均值。 您观察了什么? 为什么这样?

  播放段落

  19. Think about how to find the center of mass for any quadrilateral. Experiment and make some conjectures.
  ::19. 考虑如何为任何四边形找到质量中心。实验并作出一些推测。

  播放段落

  20. Construct the angle bisectors for any quadrilateral. Are they concurrent? Connect their intersection points to create a smaller quadrilateral called a cyclic quadrilateral. Now construct the perpendicular bisectors of the sides of the smaller quadrilateral. Are they concurrent? Construct a circle using this point as the center and one of the points on the cyclic quadrilateral. What do you observe? Can any quadrilateral be circumscribed? Explain why or why not.
  ::20. 构造任何四边形的角双扇形。 它们同时存在吗? 连接它们的交叉点以创建一个称为圆形四边形的小型四边形。 现在构造小四边形两侧的垂直双边形。 它们同时存在吗? 以此点作为圆形四边形的中心点和点之一来构造圆形。 您观察什么? 任何四边形都能被限制吗? 解释为什么或为什么不能。

  播放段落

  Review (Answers)
  ::审查(答复)

  播放段落

  Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
  ::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键 。