4.7 关于四方的理论-interactive

章节大纲

• 选择节常规

  折叠 展开

  常规

  全部折叠 展开全部

  • 选择活动新闻通告

    

    新闻通告 讨论区
• 选择节关于四方的理论

  折叠 展开

  关于四方的理论

  播放段落

  A quadrilateral is a polygon with four sides. Five special quadrilaterals are shown below, along with their definitions and pictures.
  ::四边形是一个有四面的多边形。下面显示五个特殊的四边形及其定义和图象。

  Quadrilateral	Definition	Picture
  Parallelogram	A quadrilateral with two pairs of parallel sides.
  Rectangle	A quadrilateral with four right angles .
  Rhombus	A quadrilateral with four congruent sides.
  Square	A quadrilateral with four right angles and four congruent sides.
  Kite	A convex quadrilateral with two pairs of adjacent congruent sides such that not all sides are congruent.

  播放段落

  The formal definitions of these quadrilaterals only give some information about them. Each quadrilateral has other properties that can be proved. For example, while a is defined as a quadrilateral with two pairs of parallel sides, it can be proved that the opposite sides of a parallelogram must be congruent.
  ::这些四边形的正式定义只提供了一些有关它们的信息。 每个四边形都有其他可以证明的属性。例如,虽然一个四边形被定义为具有两对平行面的四边形,但可以证明平行图的对面必须是一致的。

  播放段落

  Suppose you are given a quadrilateral and believe that it is a parallelogram. You can prove that it is a parallelogram by showing that it has two pairs of parallel sides; however, you can also use other properties that are unique to parallelograms to prove that the given shape is a parallelogram.
  ::假设您得到了一个四边形,并相信它是一个平行图。您可以通过显示它有两对平行面来证明它是一个平行图;然而,您也可以使用平行图独有的其他属性来证明给定的形状是一个平行图。

  ---

  播放段落

  Opposite Sides of a Parallelogram  are Equal
  ::平行图的对面面面相等

  播放段落

  Prove that the diagonals of a parallelogram divide the parallelogram into . Then, use this to prove that the opposite sides of a parallelogram are congruent.
  ::证明平行方形的对角将平行方形分割为 。 然后, 用它来证明平行方形的对面是相似的 。

  播放段落

  Start by drawing a generic parallelogram and previewing this proof.
  ::开始绘制通用平行图并预览此证明 。

  播放段落

  All you can assume in this proof is the definition of a parallelogram. This means that all you know is that the shape is a quadrilateral with two pairs of parallel sides. Your first goal is to prove that the diagonals divide the parallelogram into congruent triangles. You can use the parallel lines to give you congruent angles, which will help you to prove that the triangles are congruent.
  ::在此证明中, 您只能假设平行图的定义。 这意味着您只知道形状是两对平行边的四边形。 您的第一个目标是证明对角图将平行图分为相匹配的三角形。 您可以使用平行线来给您以一致角度, 这将有助于您证明三角形是相匹配的 。

  播放段落

  Your second goal is to prove that the opposite sides of the parallelogram are congruent. Since the opposite sides of the parallelogram are corresponding parts of the congruent triangles, you can use to show that they must be congruent. 
  ::您的第二个目标是证明平行图的对立面是相似的。 由于平行图的对立面是相似三角形的对应部分, 您可以用来显示它们必须是一致的 。

  播放段落

  Given: Parallelogram $\begin{align*}ABCD\end{align*}$
  ::参考:ABCD平行线形

  播放段落

  Prove: $\begin{align*}\overline{AB} \cong \overline{DC}\end{align*}$ and $\begin{align*}\overline{AD} \cong \overline{BC}\end{align*}$
  ::证明:'A'A'D'A'D'A'A'D'A'A'A'D'A'A'D'A'A'CA'A'A'CA'A'A'A'CA'A'A'A'CA'A'A'A'CA'A'A'A'CA'A'A'CA'A'A'A'D'A'A'CA'A'CA'A'A'CA'A'A'CA'A'CA'A'CA'CA'A'A'A'CA'A'A'A'A'CA'CA'C

  播放段落

  Here is a two-column proof:
  ::以下是两栏证明:

  播放段落 Statements ::声明声明 声明 声明 声明 声明 声明 声明 声明 声明 声明 声明 声明 声明 声明 声明 声明 声明 声明 声明 声明	播放段落 Reasons ::原因原因原因原因
  播放段落 Parallelogram $\begin{align*}ABCD\end{align*}$ ::ABCD 线形ABCD	播放段落 Given ::给
  播放段落 $\begin{align*}\overline{AB} \ \| \ \overline{DC}\end{align*}$ and $\begin{align*}\overline{AD} \ \| \ \overline{BC}\end{align*}$ ::#A'D'D'A'A'D'A'A'C'A'A'A'C'A'A'C'A'A'C'A'A'A'A'A'A'D'A'A'A'A'A'C'A'A'C'A'A'C'A'A'A'A'A'C'C'A'A'A'B	播放段落 Definition of a parallelogram ::平行图的定义
  播放段落 $\begin{align*}\angle BAC \cong \angle DCA \end{align*}$ ::*BACDCA - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - 播放段落 $\begin{align*}\angle ABD \cong \angle BDC \end{align*}$ ::ABD-BDC( ABD- BDC ) 播放段落 $\begin{align*}\angle DAC \cong \angle BCA\end{align*}$ ::BCA DAC BCA BCA DAC BCA BCA BCA BCA BCA BCA BCA BCA BCA BCA BCA BCA BCA BCA BCA BCA BCA BCA BCA BCA BCA BCA BCA BCA BCA 播放段落 $\begin{align*}\angle ADB \cong \angle DBC\end{align*}$ ::* 亚行*DBC	播放段落 are congruent if lines are parallel ::如果直线是平行线,则一致
  播放段落 $\begin{align*}\overline{BD} \cong \overline{BD}\end{align*}$ ::# 就会 # # Bbd # 播放段落 $\begin{align*}\overline{AC} \cong \overline{AC}\end{align*}$ ::AC'AC,AC,AC,AC,AC,AC,AC,AC,AC,AC,AC,AC,AC,AC,AC,AC,AC,AC,AC,AC,AC,AC,AC,AC,AC,AC,AC,AC,AC,AC,AC,AC,AC,AC,AC,AC,AC,AC,AC,AC,AC,AC,AC,AC,AC,AC,AC,AC,AC,AC,AC,AC,AC,AC,AC,AC,AC,AC,AC,AC,AC,AC,AC,AC,AC,AC,AC,AC,AC,AC,AC,AC,AC,AC,AC,AC,AC,AC,AC	播放段落 Reflexive Property ::弹性财产
  播放段落 $\begin{align*}\triangle ADB \cong \triangle CBD \end{align*}$ ::《生物多样性公约》 播放段落 $\begin{align*}\triangle ADC \cong \triangle CBA\end{align*}$ ::——————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————	播放段落 $\begin{align*}ASA \cong\end{align*}$ ::亚塞俄比亚州
  播放段落 $\begin{align*}\overline{AB} \cong \overline{DC}\end{align*}$ and $\begin{align*}\overline{AD} \cong \overline{BC}\end{align*}$ ::#A'D'D'A'A'D'A'A'D'A'A'D'A'A'C'A'A'A'C'A'A'A'D'A'A'A'D'A'A'C	播放段落 CPCTC ::方案协调会

  播放段落

  You have now proven two theorems about parallelograms. You can use these theorems in future proofs without proving them again.
  ::您已经证明了两个关于平行图像的理论。 您可以在未来的证明中使用这些理论, 而不再次证明它们 。

  播放段落

  Parallelogram Theorem #1: Each diagonal of a parallelogram divides the parallelogram into two congruent triangles.
  ::平行图定理 # 1: 平行图的对角将平行图分为两个相似的三角形。

  播放段落

  Parallelogram Theorem #2: The opposite sides of a parallelogram are congruent.
  ::平行图定理 # 2 : 平行图的对面是相似的 。

  播放段落

  Click the small blue arrow next to the image below and drag the orange vertices to reshape the parallelogram. Observe that the opposite sides of the parallelogram remain equal. 
  ::单击下方图像旁边的小蓝箭头,拖动橙色顶部以重塑平行图。观察平行图的对面保持相等 。

  ---

  播放段落

  Converse Parallelogram Proof
  ::反平行线形校验

  播放段落

  Prove that if a quadrilateral has opposite sides congruent, then its diagonals divide the quadrilateral into congruent triangles. Use this to prove that the quadrilateral must be a parallelogram.
  ::证明如果四边形的两面对齐, 则其对角形将四边形分割为共三角形。 以此证明四边形必须是平行图。

  播放段落

  These are the converses of the parallelogram theorems proved above. Draw a generic quadrilateral with two pairs of congruent sides and preview the proof.
  ::这些是上面证明的平行图定理的对等方。 绘制带有两对相近面的通用四边形, 并预览证据 。

  播放段落

  The  first goal is to show that the set of triangles created by each diagonal must be congruent. You can use the congruent opposite sides as well as the reflexive property to show that the triangles are congruent with $\begin{align*}SSS \cong.\end{align*}$
  ::第一个目标是显示每个对角所创建的三角形必须是相同的。 您可以使用对面的对齐三角形以及反射属性来显示三角形与 SSS 的对齐三角形 。

  播放段落

  The  second goal is to prove that the opposite sides must be parallel and so therefore the quadrilateral is a parallelogram. You can show that alternate interior angles are congruent and hence lines are parallel for this part of the proof.
  ::第二个目标是证明对立面必须是平行的, 因此四边形是一个平行图。 您可以显示其它内部角度是相似的, 因此对这部分的证明线是平行的 。

  播放段落

  Given: Quadrilateral $\begin{align*}ABCD\end{align*}$ with $\begin{align*}\overline{AB} \cong \overline{DC}\end{align*}$ and $\begin{align*}\overline{AD} \cong \overline{BC}\end{align*}$ .
  ::参考:四边ABCD 与ABDC和BC。

  播放段落

  Prove: $\begin{align*}ABCD\end{align*}$ is a parallelogram
  ::证明: ABCD 是平行图

  播放段落

  Here is a two-column proof:
  ::以下是两栏证明:

  播放段落 Statements ::声明声明 声明 声明 声明 声明 声明 声明 声明 声明 声明 声明 声明 声明 声明 声明 声明 声明 声明 声明 声明	播放段落 Reasons ::原因原因原因原因
  播放段落 $\begin{align*}\overline{AB} \cong \overline{DC}\end{align*}$ and $\begin{align*}\overline{AD} \cong \overline{BC}\end{align*}$ ::#A'D'D'A'A'D'A'A'D'A'A'D'A'A'C'A'A'A'C'A'A'A'D'A'A'A'D'A'A'C	播放段落 Given ::给
  播放段落 $\begin{align*}\overline{BD} \cong \overline{BD}\end{align*}$ ::# 就会 # # Bbd # 播放段落 $\begin{align*} \overline{AC} \cong \overline{AC}\end{align*}$ ::AC'AC,AC,AC,AC,AC,AC,AC,AC,AC,AC,AC,AC,AC,AC,AC,AC,AC,AC,AC,AC,AC,AC,AC,AC,AC,AC,AC,AC,AC,AC,AC,AC,AC,AC,AC,AC,AC,AC,AC,AC,AC,AC,AC,AC,AC,AC,AC,AC,AC,AC,AC,AC,AC,AC,AC,AC,AC,AC,AC,AC,AC,AC,AC,AC,AC,AC,AC,AC,AC,AC,AC,AC,AC,AC,AC,AC,AC,AC,AC	播放段落 Reflexive Property ::弹性财产
  播放段落 $\begin{align*}\triangle ADB \cong \triangle CBD \end{align*}$ ::《生物多样性公约》 播放段落 $\begin{align*} \triangle ADC \cong \triangle CBA\end{align*}$ ::——————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————	$\begin{align*}SSS \cong\end{align*}$
  播放段落 $\begin{align*}\angle BAC \cong \angle DCA\end{align*}$ ::*BACDCA - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - 播放段落 $\begin{align*} \angle ABD \cong \angle BDC \end{align*}$ ::ABD-BDC( ABD- BDC ) 播放段落 $\begin{align*} \angle DAC \cong \angle BCA \end{align*}$ ::BCA DAC BCA BCA DAC BCA BCA BCA BCA BCA BCA BCA BCA BCA BCA BCA BCA BCA BCA BCA BCA BCA BCA BCA BCA BCA BCA BCA BCA BCA 播放段落 $\begin{align*} \angle ADB \cong \angle DBC \end{align*}$ ::* 亚行*DBC	播放段落 CPCTC ::方案协调会
  播放段落 $\begin{align*}\overline{AB} \ \| \ \overline{DC}\end{align*}$ and $\begin{align*}\overline{AD} \ \| \ \overline{BC} \end{align*}$ ::#A'D'D'A'A'D'A'A'C'A'A'A'C'A'A'C'A'A'C'A'A'A'A'A'A'D'A'A'A'A'A'C'A'A'C'A'A'C'A'A'A'A'A'C'C'A'A'A'B	播放段落 If alternate interior angles are congruent then lines are parallel ::如果其它内部角度是相似的,则线线是平行的
  播放段落 $\begin{align*}ABCD\end{align*}$ is a parallelogram ::ABCD 是一个平行图	播放段落 Definition of a parallelogram ::平行图的定义

  播放段落

  You have now proven the converses of the first two parallelogram theorems. These are two additional ways to show that a quadrilateral is a parallelogram besides showing that the quadrilateral satisfies the definition of a parallelogram.
  ::您现在已经证明了前两个平行图定理的反义。 这些是另外两个方法来显示四边形是一个平行图, 并且表明四边形满足了平行图的定义。

  播放段落

  Parallelogram Theorem #1 Converse: If each of the diagonals of a quadrilateral divide the quadrilateral into two congruent triangles, then the quadrilateral is a parallelogram.
  ::平行图定理# 1 反面 : 如果四边形的对角将四边形分为两个相似的三角形, 那么四边形就是一个平行图。

  播放段落

  Parallelogram Theorem #2 Converse: If the opposite sides of a quadrilateral are congruent, then the quadrilateral is a parallelogram.
  ::平行图定理#2 反面:如果四边形的对面是相似的,那么四边形是平行图。

  ---

  播放段落

  Opposite Angles of  a Parallelogram are Equal
  ::对面平行形角相等

  播放段落

  To get another theorem for parallelograms, prove that the opposite angles of a parallelogram are congruent.
  ::要获得另一个平行图的定理, 证明平行图的相反角度是相似的 。

  播放段落

  Draw a generic parallelogram and preview the proof.  The goal is to prove that the opposite angles are congruent. Remember that you can use the theorems that have already been proven about parallelograms, so you can use the fact that the triangles created by the diagonals must be congruent.
  ::绘制通用平行图并预览证明。 目标是要证明相反角度是相同的。 记住您可以使用已经通过平行图被证明的定理, 这样您就可以使用对角图创建的三角形必须是一致的这一事实 。

  播放段落

  Given: Parallelogram $\begin{align*}ABCD\end{align*}$ .
  ::参考:ABCD线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线。

  播放段落

  Prove: $\begin{align*}\angle A \cong \angle C \end{align*}$ and $\begin{align*}\angle B \cong \angle D \end{align*}$
  ::证明: @AC和#BD

  播放段落

  Here is a paragraph proof:
  ::以下是一段证据:

  播放段落

  Because each diagonal of a parallelogram divides the parallelogram into two congruent triangles, $\begin{align*}\triangle ADB \cong \triangle CBD \end{align*}$ and $\begin{align*}\triangle ADC \cong \triangle CBA \end{align*}$ . $\begin{align*}\angle A\end{align*}$ and $\begin{align*}\angle C\end{align*}$ are corresponding parts of $\begin{align*}\triangle ADB\end{align*}$ and $\begin{align*}\triangle CBD\end{align*}$ . Similarly, $\begin{align*}\angle B\end{align*}$ and $\begin{align*}\angle D\end{align*}$ are corresponding parts of $\begin{align*}\triangle ADC\end{align*}$ and $\begin{align*}\triangle CBA\end{align*}$ . This means that $\begin{align*}\angle A \cong \angle C\end{align*}$ and $\begin{align*}\angle B \cong \angle D\end{align*}$ because .
  ::因为平行图的对角将平行图分为两个相似的三角形,所以“ADB”和“AADCC”是“ADB”和“CBD”的对应部分。同样,“B”和“D”是“ADC”和“CBA”的对应部分。这意味着“AC”和“BD”是“因为”的对应部分。

  播放段落

  You have now proven a third theorem about parallelograms. You can use this theorem in future proofs without proving it again.
  ::您已经证明了关于平行图象的第三个理论。 您可以在未来的证明中使用这个理论, 而不再次证明它 。

  播放段落

  Parallelogram Theorem #3: The opposite angles of a parallelogram are congruent.
  ::3号平行图定理:平行图的相反角度是相同的。

  播放段落

  Click the small blue arrow next to the image below and drag the orange vertices to reshape the parallelogram. Observe that the opposite angles of the parallelogram remain equal. 
  ::单击下方图像旁边的小蓝箭头,拖动橙色顶部以重塑平行图。观察平行图的对角保持相等 。

  ---

  播放段落

  Diagonals of a Parallelogram Bisect Each Other
  ::平行相形相形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形体

  播放段落

  Prove that the diagonals of a parallelogram bisect each other.
  ::证明平行方形的对角线 互相交叉

  播放段落

  Draw a generic parallelogram and preview the proof.
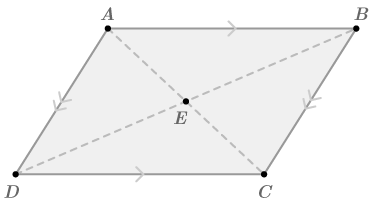
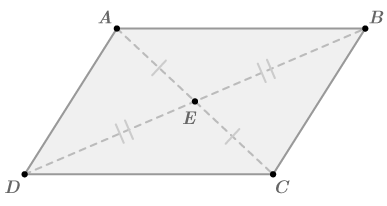
  ::绘制通用平行图并预览证明。

  

  播放段落

  What does it mean for the diagonals to bisect each other? If the diagonals bisect each other then each diagonal crosses the other diagonal at its midpoint . This would mean that $\begin{align*}\overline{AE} \cong \overline{EC}\end{align*}$ and $\begin{align*}\overline{ED} \cong \overline{BE}\end{align*}$ .
  ::如果对角线相互对立,那么对角线在中间点交叉对角线。这意味着“AE”和“EE”。

  播放段落

  Your goal is to use the parallelogram definition and theorems to show that $\begin{align*}\overline{AE} \cong \overline{EC}\end{align*}$ and $\begin{align*}\overline{ED} \cong \overline{BE}\end{align*}$ . First, try to prove that the two diagonals divide the parallelogram into four small triangles, and each pair of these triangles is congruent.
  ::你的目标是使用平行图像定义和理论来显示 AE EC 和ED BE。 首先,试图证明两个对角将平行图像分为四个小三角形,这些三角形的每对是相同的。

  播放段落

  Given: Parallelogram $\begin{align*}ABCD\end{align*}$
  ::参考:ABCD平行线形

  播放段落

  Prove: $\begin{align*}\overline{AE} \cong \overline{EC} \end{align*}$ and $\begin{align*}\overline{ED} \cong \overline{BE}\end{align*}$ (the diagonals bisect each other)
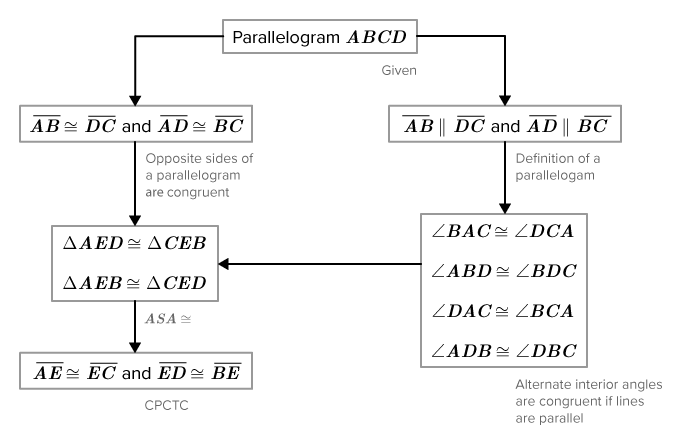
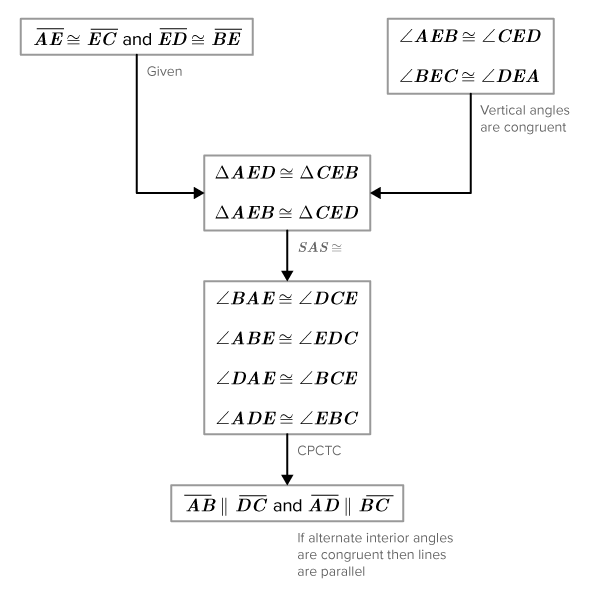
  ::证明:AEEEEEE和EEEEEE(对角线对齐)

  播放段落

  Here is a flow diagram proof.

  

  
  ::这是流程图的证明

  播放段落

  You have now proven the fourth theorem about parallelograms. You can use this theorem in future proofs without proving it again.
  ::您已经证明了关于平行图象的第四个定理。 您可以在未来的证明中使用这个定理, 而不再次证明它 。

  播放段落

  Parallelogram Theorem #4: The diagonals of a parallelogram bisect each other.
  ::平行图定理4: 平行图双形的对角。

  播放段落

  Click the small blue arrow next to the image below and drag the orange vertices to reshape the parallelogram. Observe how the diagonals of the parallelogram bisect each other. 
  ::单击下方图像旁边的小蓝箭头,拖动橙色顶部以重塑平行图。观察平行图双形的对角如何相互分割。

  ---

  播放段落

  Examples
  ::实例实例实例实例

  播放段落

  Example 1
  ::例1

  播放段落

  Is a rectangle a parallelogram? If so, what does this mean about the properties of a rectangle?
  ::矩形是平行图吗 ? 如果是, 这对矩形的属性意味着什么 ?

  播放段落

  To prove that a rectangle is a parallelogram, you must prove that it either satisfies the definition of a parallelogram or satisfies any of the theorems that prove that quadrilaterals are parallelograms.
  ::要证明矩形是平行图, 您必须证明它既符合平行图的定义, 也符合任何能证明四边形是平行图的理论。

  播放段落

  A rectangle is a quadrilateral with four right angles. You can use these angles to show that the opposite sides of a rectangle must be parallel.
  ::矩形是四个右角度的四边形。您可以使用这些角度来显示矩形的对面必须平行。

  播放段落

  Given: Rectangle $\begin{align*}ABCD\end{align*}$
  ::给定值: 矩形 ABCD

  播放段落

  Prove: $\begin{align*}\overline{AB} \ \| \ \overline{DC}\end{align*}$ and $\begin{align*}\overline{AD} \ \| \ \overline{BC}\end{align*}$
  ::证明:'A'A'D'A'D'A'A'A'D'A'A'A'A'C'A'A'A'A'C'A'A'A'A'A'A'A'C'A'A'A'A'A'A'A'A'A'A'A'A'A'A'A'A'A'A'A'A'A'A'A'A'A'A'C

  播放段落

  Here is a paragraph proof:
  ::以下是一段证据:

  播放段落

  A rectangle has four right angles by definition, so $\begin{align*}m \angle A=m \angle B=m \angle C=m \angle D=90^\circ\end{align*}$ . $\begin{align*}\angle A\end{align*}$ and $\begin{align*}\angle D\end{align*}$ are . $\begin{align*}m \angle A+m \angle D=180^\circ\end{align*}$ , which means that $\begin{align*}\angle A\end{align*}$ and $\begin{align*}\angle D\end{align*}$ are supplementary. If same side interior angles are supplementary, then lines are parallel. This means that $\begin{align*}\overline{AB} \ \| \ \overline{DC}\end{align*}$ . Similarly, $\begin{align*}\angle A \end{align*}$ and $\begin{align*}\angle B \end{align*}$ are same side interior angles. $\begin{align*}m \angle A+m \angle B=180^\circ\end{align*}$ , which means that $\begin{align*}\angle A\end{align*}$ and $\begin{align*}\angle B\end{align*}$ are supplementary. If same side interior angles are supplementary, then lines are parallel. This means that $\begin{align*}\overline{AD} \ \| \ \overline{BC}\end{align*}$ .
  ::矩形按定义有四个右角, 所以 mA=mB=mC=mD=90。 A和D是. mA+mD=180, 意思是A和D是补充的。 如果对齐侧内角是补充的, 那么线是平行的。 这意味着“ AB” =DC。 同样, A 和B是相同的侧侧内角。 mA+mB=180, 这意味着“ A”和“ B”是补充的。 如果对齐侧内角是补充的, 那么线是平行的。 这意味着“ 肯定 ” 。

  播放段落

  You have proven that a rectangle is a parallelogram.
  ::您已经证明了矩形是一个平行图。

  播放段落

  Rectangle Theorem #1: A rectangle is a parallelogram.
  ::矩形定理 # 1 : 矩形是平行图。

  播放段落

  This means that have all the same properties as parallelograms. Like parallelograms, rectangles have opposite sides congruent and parallel and diagonals that bisect each other.
  ::这意味着与平行图具有相同的属性。 矩形与平行图一样, 相形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形色形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形形

  播放段落

  Example 2
  ::例2

  播放段落

  Prove that the diagonals of a rectangle are congruent.
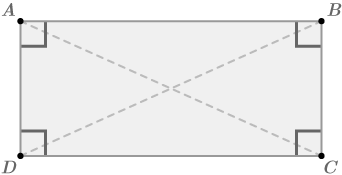
  ::证明矩形的对角线是相容的

  播放段落

  Draw a rectangle with its diagonals and preview the proof. To prove that the diagonals are congruent, you will first want to prove that $\begin{align*}\triangle ADC \cong \triangle BCD\end{align*}$ . These are two right triangles and their hypotenuses are the diagonals of the rectangle. If you can prove that these two right triangles are congruent, then you can prove that the diagonals are congruent.
  ::绘制矩形, 并预览其对角形。 要证明对角形是一致的, 您首先要证明 {ADC\\\BCD 。 这是两个右三角形, 它们的下限是矩形的对角形。 如果您能证明这两个右三角形是一致的, 那么您就可以证明对角形是一致的 。

  

  播放段落

  Given: Rectangle $\begin{align*}ABCD\end{align*}$
  ::给定值: 矩形 ABCD

  播放段落

  Prove: $\begin{align*}\overline{AC} \cong \overline{BD}\end{align*}$
  ::证明:

  播放段落

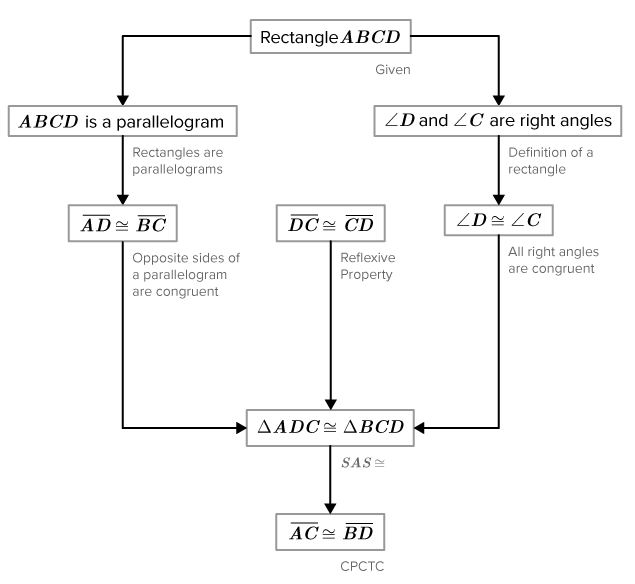
  Here is a flow diagram proof:
  ::以下是流程图证明:

  

  播放段落

  You have proven that a rectangle has congruent diagonals. You can now use this theorem in future proof.
  ::您已经证明矩形具有相容的对角线。 现在您可以在未来的证明中使用此定理 。

  播放段落

  Rectangle Theorem #2: A rectangle has congruent diagonals.
  ::矩形定理 #2: 矩形具有相似的对数法。

  播放段落

  Example 3
  ::例3

  播放段落

  Prove that if a quadrilateral has diagonals that bisect each other, then it is a parallelogram.
  ::证明如果一个四边形的对角线 相互交叉,那么它就是一个平行图。

  播放段落

  This is the converse of parallelogram theorem #4 from guidance. Draw a quadrilateral with diagonals that bisect each other and preview the proof.
  ::这是向导中平行图定理 # 4 的对立面。 绘制一个带有对角的四边形, 相互交叉并预览证据 。

  

  播放段落

  Your goal will be to show that there are two pairs of congruent triangles created by these diagonals. Then, you can show that alternate interior angles are congruent and therefore the opposite sides must be parallel.
  ::您的目标将是显示有两对相似的三角形是由这些对角形创建的。 然后, 您可以显示其它的内部角度是相同的, 因此对立面必须是平行的 。

  播放段落

  Given: $\begin{align*}\overline{AE} \cong \overline{EC}\end{align*}$ and $\begin{align*}\overline{ED} \cong \overline{BE}\end{align*}$
  :AEE) (EE) (EE) (EE) (EE) (E) (E) (E) (E) (E) (E) (E) (E) (E) (E) (E) (E) (E) (E) (E) (E) (E) (E) (E) (E) (E)

  播放段落

  Prove: $\begin{align*}\overline{AB} \ \| \ \overline{DC}\end{align*}$ and $\begin{align*}\overline{AD} \ \| \ \overline{BC}\end{align*}$ ( $\begin{align*}ABCD\end{align*}$ is a parallelogram)
  ::证明: 'AB 'DC' and'AD' BC' (ABCD是一个平行图)

  播放段落

  Here is a flow diagram proof:
  ::以下是流程图证明:

  

  播放段落

  You have now proven the converse of the fourth parallelogram theorem. This is one additional way to show that a quadrilateral is a parallelogram.
  ::您已经证明了第四个平行图定理的反义。 这是另外一种显示四边形是平行图的方法 。

  播放段落

  Parallelogram Theorem #4 Converse: If the diagonals of a quadrilateral bisect each other, then the quadrilateral is a parallelogram.
  ::平行图定理 # 4 : 如果四边形的对角相对, 则四边形是平行图。

  播放段落

  Example 4
  ::例4

  播放段落

  Prove that a rhombus is a parallelogram. What does this tell you about the properties of a rhombus?
  ::证明暴龙是一个平行图。这告诉你什么有关暴龙的特性?

  播放段落

  Is a rhombus a parallelogram? This would mean that a rhombus has opposite sides that are parallel. To prove that a rhombus is a parallelogram, you must prove that it either satisfies the definition of a parallelogram or satisfies any of the theorems that prove that quadrilaterals are parallelograms.
  ::圆柱形是平行图吗? 这意味着圆柱形是平行面。 要证明圆柱形是平行图, 您必须证明它符合平行图的定义, 或者符合任何能够证明四边形是平行图的理论。

  播放段落

  Here is a paragraph proof:
  ::以下是一段证据:

  播放段落

  A rhombus is a quadrilateral with four congruent sides, therefore opposite sides of a rhombus are congruent. Parallelogram theorem #2 converse states that "if the opposite sides of a quadrilateral are congruent, then the quadrilateral is a parallelogram". Therefore, a rhombus is a parallelogram.
  ::圆柱形是一个四边形的四边形,四面形相同,因此圆柱形的对面是相似的。 平行方形的理论2对立写道 , “ 如果四边形的对立面是相似的, 那么四边形是平行的。 ” 因此, 圆柱形是平行的。

  播放段落

  You have proven that a rhombus is a parallelogram.
  ::你已经证明 暴风车是一个平行图。

  播放段落

  Rhombus Theorem #1: A rhombus is a parallelogram.
  ::Rhombus Theorem # 1 : 暴风车是一个平行图。

  播放段落

  This means that rhombuses have all the same properties as parallelograms. Like parallelograms, rhombuses have opposite sides parallel, opposite angles congruent and diagonals that bisect each other.
  ::这意味着 伦布斯 与 平行 图形 具有 相同 的 属性 。 与 平行 图形 一样, 伦布斯 具有 相向 的 平行 、 相对 和 对角 的 平行 、 相对 、 相对 、 相对 、 相对 、 相对 、 相对 、 相对 。

  播放段落

  Example 5
  ::例5

  播放段落

  Prove that the diagonals of a rhombus bisect its angles and are perpendicular to each other.
  ::证明暴龙的对角线将两角度分开,相互垂直。

  播放段落

  A rhombus is a parallelogram, therefore the diagonals bisect each other. Draw a generic rhombus with diagonals. Your first goal is to prove that the two diagonals divide the rhombus into four small congruent triangles. Since the angles of the rhombus are corresponding parts of the congruent triangles, you can use CPCTC to show that the diagonals bisect its angles.
  ::圆柱形是一个平行的图形, 因此对角形是相交的。 用对角形绘制一个普通的对角形。 您的第一个目标是证明两个对角形将圆柱形分为四个小相匹配的三角形。 由于圆柱形角是对齐三角形的对应部分, 您可以使用 CPCCT 来显示对角形对齐角。

  播放段落

  Your second goal is to prove that the diagonals are perpendicular. You can show that the small congruent triangles are right triangles and hence diagonals are perpendicular.
  ::您的第二个目标是证明对角线是垂直的。 您可以显示小的对角三角形是正确的三角形, 因此对角线是垂直的 。

  播放段落

  Given: Rhombus $\begin{align*}ABCD\end{align*}$ whose diagonals $\begin{align*}\overline{AC}\end{align*}$ and $\begin{align*}\overline{BD}\end{align*}$ intersect at $\begin{align*}O\end{align*}$ .
  ::Rhombus ABCD, 其对角的AC和O交叉。

  播放段落

  To prove: $\begin{align*}\angle AOB = \angle AOD = \angle BOC = \angle DOC = 90^\circ\end{align*}$
  ::证明:

  播放段落

  Here is a two-column proof:
  ::以下是两栏证明:

  	Statements	Reasons
  	$\begin{align*}ABCD\end{align*}$ is a rhombus $\begin{align*}\Rightarrow\end{align*}$ $\begin{align*}ABCD\end{align*}$ is a parallelogram
  $\begin{align*}\Rightarrow\end{align*}$	$\begin{align*}\overline{AB} \cong \overline{BC} \cong \overline{CD} \cong \overline{DA}\end{align*}$	Sides of rhombus are congruent
  	$\begin{align*}\overline{OB} = \overline{OD}\end{align*}$ and $\begin{align*}\overline{OA }= \overline{OC}\end{align*}$	Diagonals of a parallelogram bisect each other
  In $\begin{align*}\triangle BOC\end{align*}$ and $\begin{align*}\triangle DOC,\end{align*}$
  	$\begin{align*}\overline{BO} = \overline{DO}\end{align*}$	Diagonals of a parallelogram bisect each other
  	$\begin{align*}\overline{BC} =\overline{ DC}\end{align*}$	Definition of a rhombus
  	$\begin{align*}\overline{OC }=\overline{ OC}\end{align*}$	Reflexive property
  	$\begin{align*}\triangle BOC \cong \triangle DOC\end{align*}$	$\begin{align*}SSS \cong\end{align*}$
  	$\begin{align*}\angle BCO \cong \angle DCO\end{align*}$	CPCTC
  	$\begin{align*}\angle BOC \cong \angle DOC\end{align*}$	CPCTC
  	But $\begin{align*}\angle BOC + \angle DOC = 180^\circ\end{align*}$	Linear pair
  $\begin{align*}\therefore\end{align*}$	$\begin{align*}\angle BOC = \angle DOC =90^\circ\end{align*}$
  	Similarly, $\begin{align*}\angle AOB = \angle AOD = 90^\circ\end{align*}$

  播放段落

  You have now proven that diagonals of a rhombus bisect its angles and are perpendicular to each other.
  ::你们已经证明 红云的对角线 将两角度分开 并且相互垂直

  播放段落

  Rhombus Theorem #2: The diagonals of a rhombus are perpendicular.
  ::Rhombus Theorem # 2: 伦布鲁斯的对角是垂直的。

  播放段落

  Rhombus Theorem #3: The diagonals of a rhombus bisect its angles.
  ::Rhombus Theorem # 3: 龙卷风的对角线,

  播放段落

  Click the small blue arrow next to the image below and drag the orange vertices to reshape the rhombus. Observe that the diagonals of a rhombus are perpendicular to each other and each of the diagonals bisects its vertex angles.
  ::单击下方图像旁边的蓝色小箭头,拖动橙色的脊椎来重塑矩形。注意,矩形对角的对角是垂直的,对角的对角对齐其顶角。

  播放段落

  Example 6
  ::例6

  播放段落

  Prove that one diagonal of a bisects its angles.
  ::证明一个两分形的对角 能够分辨出其角度

  播放段落

  A kite is a quadrilateral with adjacent sides congruent. Draw a generic kite with one diagonal. Your goal is to prove that only one diagonal divides the kite into two congruent triangles. Since the angles of the kite are corresponding parts of the congruent triangles, you can use CPCTC to show that the diagonal bisects its angles.
  ::风筝是一个四边形, 与相邻的侧面相似。 绘制一个带有一个对角的通用风筝。 您的目标是要证明只有一个对角形将风筝分割成两个相似的三角形。 由于风筝的角度是相近三角形的对应部分, 您可以使用 CPCTC 来显示对角形的两边角角。

  播放段落

  Given: Kite $\begin{align*}ABCD\end{align*}$ with $\begin{align*}\overline{AB} \cong \overline{AD}\end{align*}$ and $\begin{align*}\overline{CB} \cong \overline{CD}\end{align*}$ .
  ::基特ABCD与ABAA和CBCD。

  播放段落

  To prove: $\begin{align*}\overline{AC}\end{align*}$ bisects $\begin{align*}\angle BAD\end{align*}$ and $\begin{align*}\angle BCD\end{align*}$ .
  ::证明:"BAD"和"BCD"的两分

  播放段落

  Here is a two-column proof:
  ::以下是两栏证明:

  Statements	Reasons
  $\begin{align*}\overline{AB} \cong \overline{AD}\end{align*}$ and $\begin{align*}\overline{CB} \cong \overline{CD}\end{align*}$	Definition of a kite
  $\begin{align*}\overline{AC} \cong \overline{AC}\end{align*}$	Reflexive property
  $\begin{align*}\triangle ABC \cong \triangle ADC\end{align*}$	$\begin{align*}SSS \cong\end{align*}$
  $\begin{align*}\angle BAC \cong \angle DAC\end{align*}$	CPCTC
  $\begin{align*}\angle BCA \cong \angle DCA\end{align*}$	CPCTC

  播放段落

  Thus, $\begin{align*}\overline{AC}\end{align*}$ bisects $\begin{align*}\angle BAD\end{align*}$ and $\begin{align*}\angle BCD\end{align*}$ forming two congruent angles. If you draw diagonal $\begin{align*}\overline{BD}\end{align*}$ , $\begin{align*}\angle ABD \ncong \angle CBD\end{align*}$ and $\begin{align*}\angle ADB \ncong \angle CDB\end{align*}$ since $\begin{align*}\overline{BC} \ncong \overline{BA}\end{align*}$ and $\begin{align*}\overline{DC} \ncong \overline{DA}\end{align*}$ , by definition of a kite.
  ::因此,“BAD”和“BCD”的两部分组成了两个相似的角度。如果绘制对角“BD”、“ABD”和“ABD”和“ADBCD,则根据风筝的定义,从BCB和DC'DA开始。

  播放段落

  You have now proven that only one diagonal of a kite bisects its angles.
  ::你现在已经证明 风筝两侧只有一个对角 就能分辨出它的角度

  播放段落

  Kite Theorem #1: One diagonal of a kite bisects its angles.
  ::Kite Theorem # 1 : 风筝的对角线将角度分成两部分 。

  播放段落

  Example 7
  ::例7

  播放段落

  Prove that a kite has one pair of opposite angles congruent.
  ::证明风筝有一对对相反角度的一致

  播放段落

  A kite is a quadrilateral with adjacent sides congruent. Draw a generic kite with one diagonal. Your goal is to prove that only one diagonal divides the kite into two congruent triangles. Since the angles of the kite are corresponding parts of the congruent triangles, you can use CPCTC to show that only one pair of opposite angles are congruent.
  ::风筝是一个四边形, 与相邻的侧面相似。 绘制一个带有一个对角的通用风筝。 您的目标是要证明只有一个对角形将风筝分割成两个相近的三角形。 由于风筝的角度是相近三角形的对应部分, 您可以使用 CPCTC 来显示只有一对对对对角是相近的。

  播放段落

  Given: Kite $\begin{align*}ABCD\end{align*}$ with $\begin{align*}\overline{AB} \cong \overline{AD}\end{align*}$ and $\begin{align*}\overline{CB} \cong \overline{CD}\end{align*}$ .
  ::基特ABCD与ABAA和CBCD。

  播放段落

  To prove: $\begin{align*}\angle B \cong \angle D\end{align*}$ and $\begin{align*}\angle A \ncong \angle C\end{align*}$
  ::证明:##BD和#AC

  播放段落

  Here is a two-column proof:
  ::以下是两栏证明:

  Statements	Reasons
  $\begin{align*}\overline{AB} \cong \overline{AD}\end{align*}$ and $\begin{align*}\overline{CB} \cong \overline{CD}\end{align*}$	Definition of a kite
  $\begin{align*}\overline{AC} \cong \overline{AC}\end{align*}$	Reflexive property
  $\begin{align*}\triangle ABC \cong \triangle ADC\end{align*}$	$\begin{align*}SSS \cong\end{align*}$
  $\begin{align*}\angle B \cong \angle D\end{align*}$	CPCTC

  播放段落

  Thus, one pair of opposite angles are congruent. If $\begin{align*}\angle A \cong \angle C\end{align*}$ , then the quadrilateral will have two pairs of opposite angles congruent. This means $\begin{align*}ABCD\end{align*}$ is a parallelogram. The above statement is a contradiction - as a kite is not a parallelogram. You cannot have a kite that is a parallelogram. So, if a quadrilateral is a kite, it has only one pair of opposite angles congruent.
  ::因此,一对相反角度是相同的。 如果 AC, 则四边形将具有两对相反角度是相同的。 这意味着 ABCD 是一个平行的图象。 上面的语句是矛盾的 - 因为风筝不是平行的图象。 您不能有一个平行图象的风筝。 因此, 如果四边形是风筝, 它只有一对相反角度是相同的。

  播放段落

  Click the small blue arrow next to the image below and drag the orange vertices to reshape the kite. Observe that one pair of opposite angles are congruent and how one diagonal of a kite bisects its angles.
  ::单击下方图像旁边的蓝色小箭头,拖动橙色的脊椎来重塑风筝。注意一对相反角度是相似的,风筝的对角如何对齐。

  Summary

  播放段落 A quadrilateral is a polygon with four sides.  ::四边形是四面多边形。 播放段落 A parallelogram is a quadrilateral with two pairs of parallel sides. ::平行图是四边形,两对平行面。 播放段落 A rectangle is a quadrilateral with four right angles. ::矩形是四个右角度的四边形。 播放段落 A rhombus is a quadrilateral with four congruent sides. ::圆柱形是四边形,四面相容。 播放段落 A square is a quadrilateral with four right angles and four congruent sides. ::方形是四边形,有四个右角度和四个相容的方形。 播放段落 A kite is a convex quadrilateral with two pairs of adjacent congruent sides such that not all sides are congruent. ::风筝是一个共和的四边形,有两对相邻的相近相近面,因此并非所有两边都是一致的。

  ---

  播放段落

  Review
  ::审查审查审查审查

  播放段落

  1. State the definition of a parallelogram and three additional properties of a parallelogram.
  ::1. 说明平行图的定义和平行图的另外三个特性。

  播放段落

  2. State the definition of a rectangle and four additional properties of a rectangle.
  ::2. 说明矩形的定义和矩形的另外四个特性。

  播放段落

  3. Use the rhombus below to prove that a rhombus has perpendicular diagonals.
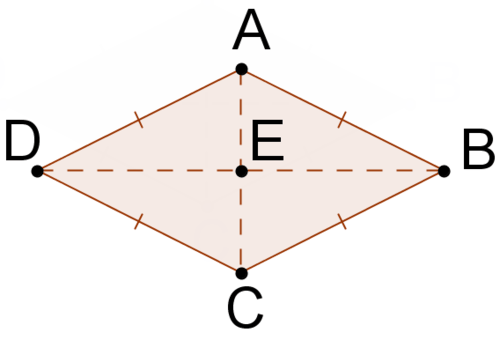
  ::3. 使用下面的红外线来证明红外线有垂直对角线。

  

  播放段落
  • Use the definition of a rhombus and the theorems about parallelograms to prove that $\begin{align*}\triangle AED \cong \triangle AEB\end{align*}$ .
    ::使用暴风雨的定义和平行图的定理来证明“AAED”和“AEB”。
  播放段落
  • Prove that $\begin{align*}m \angle AED=m \angle AEB\end{align*}$ .
    ::证明一下
  播放段落
  • Prove that $\begin{align*}\angle AED\end{align*}$ is a right angle.
    ::证明ZAED是正确角度
  播放段落
  • Prove that $\begin{align*}AC \perp DB\end{align*}$ .
    ::证明ACDB。

  播放段落

  4. Use the rhombus below to prove that a rhombus has diagonals that bisect its angles.
  ::4. 使用下面的红外线来证明红外线有两面形,两面分角。

  

  播放段落
  • Use the definition of a rhombus and the theorems about parallelograms to prove that $\begin{align*}\triangle ADC \cong \triangle ABC\end{align*}$ and $\begin{align*}\triangle ADB \cong \triangle CDB\end{align*}$ .
    ::使用暴风雨的定义和平行图的理论来证明“ADCABC”和“ADBCDB”。
  播放段落
  • Prove that there are congruent angles and therefore the diagonals have bisected the angles.
    ::证明有相似的角 因此对角体将角分成两部分

  播放段落

  5. State the definition of a rhombus and five additional properties of a rhombus.
  ::5. 说明暴风车的定义和暴风车的另外五种特性。

  播放段落

  6. Is a square a rectangle? Is a square a rhombus? Explain.
  ::6. 方形是矩形吗?

  播放段落

  7. Is a square a parallelogram? Explain.
  ::7. 方形是平行图吗?

  播放段落

  8. State the definition of a square and five additional properties of a square.
  ::8. 说明一个广场的定义和一个广场的另外五个属性。

  播放段落

  Use the kite below for the proofs in #9-#13.
  ::使用下面的风筝作为#9 -13的证明。

  

  播放段落

  9. Prove that one diagonal of a kite divides it into two congruent triangles.
  ::9. 证明风筝的一个对角将它分为两个相似的三角形。

  播放段落

  10. Prove that a kite has one pair of opposite angles congruent. Hint: Use the result to #9!
  ::10. 证明风筝具有一对对相反角度的一致。 提示:将结果使用到 # 9 !

  播放段落

  11. Prove that one diagonal of a kite bisects its angles. Hint: Draw the diagonal that bisects its angles. Use the result of #9 and then CPCTC.
  ::11. 证明风筝两侧角有一个对角。 提示: 绘制两侧角的对角, 使用 # 9 和 CPCCT 的结果 。

  播放段落

  12. Prove that one diagonal of a kite is bisected by another diagonal. Hint: Draw both diagonals. Prove that two of the four small triangles are congruent and then use CPCTC. Use the result of #11 to help.
  ::12. 证明风筝的一个对角体被另一个对角体双切。 提示 : 绘制两个对角体 。 证明四个小三角体中有两个是相似的, 然后使用 CPCTC 。 使用 # 11 的结果来帮助 。

  播放段落

  13. Prove that the diagonals of a kite are perpendicular. Hint: Use the result of #11 and a similar method to the one that was used in #3!
  ::13. 证明风筝的对角线是垂直的。 提示 : 使用 # 11 的结果和与 # 3 中使用的方法相似的方法 !

  播放段落

  14. State the definition of a kite and four additional properties of a kite.
  ::14. 说明风筝的定义和风筝的四个额外特性。

  播放段落

  15. Use the picture below with $\begin{align*}\overline{AC} \cong \overline{BD}\end{align*}$ to help prove that a parallelogram with congruent diagonals is a rectangle.
  ::15. 使用以下的图片与“AC”和“BD”一起帮助证明,与正对立面相匹配的平行图是一个矩形。

  

  播放段落

  16. Use the picture below to help prove that a quadrilateral with opposite angles congruent is a parallelogram. Hint: Use the fact that the sum of the interior angles of a quadrilateral is $\begin{align*}360^\circ\end{align*}$ .
  ::16. 利用下面的图象来证明一个角度对齐的四边形是一个平行图象。 提示: 使用四边形内角的总和是360\\\\\。

  

  播放段落

  17. An isosceles trapezoid has two congruent legs. One of the properties of an isosceles trapezoid is that base angles (formed with either base) are congruent. You may use that property in the following proof. Prove that diagonals in an isosceles trapezoid are congruent.
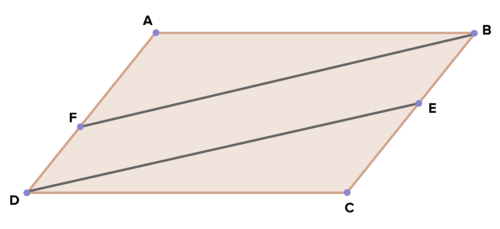
  ::17. 等离子体捕鲸类有两条相似的腿,一个等离子体捕鲸类的特性之一是基角度(与基底或基底形成)是相同的。在以下证据中可以使用该属性。证明等离子体捕鲸类的对角是同质的。

  播放段落

  18. Given: ABCD is a parallelogram; $\begin{align*}\overline {AF} \cong \overline{CE}\end{align*}$
  ::18. 参考:ABCD是一个平行图;A'A'CE

  播放段落

  Prove: $\begin{align*}\overline{FB}\cong\overline{DE}\end{align*}$
  ::证明:

  

  播放段落

  19. Prove that if one pair of sides in a quadrilateral is both congruent and parallel, then the quadrilateral is a parallelogram.
  ::19. 证明如果四边形的一对对两对是一致和平行的,那么四边形是平行的。

  播放段落

  Review (Answers)
  ::审查(答复)

  播放段落

  To see the answer key for this book, go to the and click on the Answer Key under the ' ' option.
  ::要查看本书的答案键, 请在“ ” 选项下点击答案键 。