6.6 涉及相似性的理论-interactive

Section outline

• Select section General

  Collapse Expand

  General

  Collapse all Expand all

  • Select activity 新闻通告

    

    新闻通告 Forum
• Select section 涉及相似性的理论论

  Collapse Expand

  涉及相似性的理论论

  播放段落

  If two triangles are similar , then their are congruent and their corresponding sides are proportional.
  ::如果两个三角形相似,那么它们就是相似的,它们对应的两边是成比例的。

  播放段落

  There are many theorems about triangles that you can prove using similar triangles . Here are three of them:
  ::有关三角形的许多定理,您可以用相似的三角形来证明。这里有三个:

  播放段落
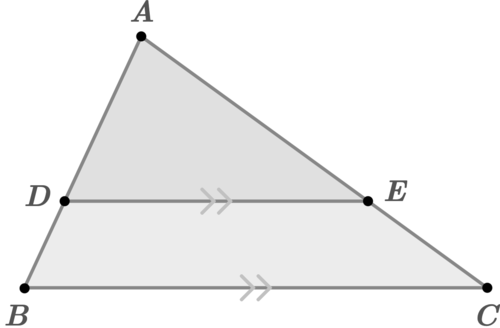
  1. Triangle Proportionality Theorem : A line parallel to one side of a triangle divides the other two sides of the triangle proportionally.
     ::三角比例定理:三角形对齐的一条线将三角形对面的另外两边成比例地分隔开来。
  播放段落
  2. Triangle Angle Bisector Theorem : The angle bisector of one angle of a triangle divides the opposite side of the triangle into segments proportional to the lengths of the other two sides of the triangle.
     ::三角三角形 Angle 双区定理 : 三角形角的一个角的角角两部分将三角形对面的三角形对面分隔为与三角形其他两边长度成正比的区段 。
  播放段落
  3. Pythagorean Theorem : For a right triangle with legs $\begin{align*}a\end{align*}$ and $\begin{align*}b\end{align*}$ and hypotenuse $\begin{align*}c:\end{align*}$    $\begin{align*}a^2+b^2=c^2.\end{align*}$
     ::Pytagorean 理论: 右三角形, 右三角形, 腿 a 和 b , 下角 c: a2+b2= c2 。

  ---

  播放段落

  Triangle Similarity Proof
  ::三角形相似性证明

  播放段落

  Prove that $\begin{align*}\triangle ADE \thicksim \triangle ABC.\end{align*}$
  ::证明ADEABC。

  	Statements	Reasons
  In $\begin{align*}\triangle ABC\end{align*}$ and $\begin{align*}\triangle ADE\end{align*}$ ,
  	$\begin{align*}\angle ABC\end{align*}$ $\begin{align*}=\end{align*}$ $\begin{align*}\angle ADE\end{align*}$	Corresponding angles
  	$\begin{align*}\angle ACB\end{align*}$ $\begin{align*}=\end{align*}$ $\begin{align*}\angle AED\end{align*}$	Corresponding angles
  	$\begin{align*}\angle BAC\end{align*}$ $\begin{align*}=\end{align*}$ $\begin{align*}\angle DAE\end{align*}$	Common (shared angle)
  $\begin{align*}\therefore\end{align*}$	$\begin{align*}\triangle ABC \sim \triangle ADE\end{align*}$	by $\begin{align*}AA\end{align*}$ similarity

  ---

  播放段落

  Triangle Proportionality Theorem
  ::三角交配性定理

  播放段落

  Given $\begin{align*}\triangle ADE \sim \triangle ABC,\end{align*}$  first prove that $\begin{align*}\frac{AB}{AD}=\frac{AC}{AE},\end{align*}$  then use algebra to show that $\begin{align*}\frac{DB}{AD}=\frac{EC}{AE}.\end{align*}$
  ::并使用代数来显示DBAD=ECAE。

  

  播放段落

  You know that $\begin{align*}\triangle ADE \sim \triangle ABC,\end{align*}$ which means that corresponding sides are proportional. Therefore, $\begin{align*}\frac{AB}{AD}=\frac{AC}{AE}\end{align*}$ .
  ::你知道,ABAD=ACAE。所以,ABAD=ACAE。

  播放段落

  U se algebra to show that the second proportion must be true.
  ::使用代数来显示第二比例必须是真实的。

  	Statements	Reasons
  	$\begin{align*}\frac{AB}{AD} = \frac{AC}{AE}\end{align*}$	Corresponding sides of similar triangles are proportional
  $\begin{align*}\Rightarrow\end{align*}$	$\begin{align*} \frac{AD + DB}{AD} = \frac{AE + EC}{AE}\end{align*}$
  $\begin{align*}\Rightarrow\end{align*}$	$\begin{align*} 1 + \frac{DB}{AD} = 1 + \frac{EC}{AE}\end{align*}$	$\begin{align*}\frac{AD}{AD}=1; \frac{AE}{AE} =1\end{align*}$
  $\begin{align*}\Rightarrow\end{align*}$	$\begin{align*} \frac{DB}{AD} = \frac{EC}{AE}\end{align*}$	After subtracting 1 from both sides

  播放段落

  You have now proved the triangle proportionality theorem, which states that a line parallel to one side of a triangle divides the other two sides of the triangle proportionally .
  ::您现在已经证明了三角比例定理, 它指出三角形的一面平行的线将三角形的另外两面按比例分隔。

  ---

  播放段落

  Triangle Bisector Theorem 
  ::三角边边边边边段定理

  播放段落

  Consider $\begin{align*}\triangle ABC\end{align*}$ with $\begin{align*}\overline{AE}\end{align*}$ the angle bisector of $\begin{align*}\angle BAC\end{align*}$ and point $\begin{align*}D\end{align*}$ constructed so that $\begin{align*}\overline{DC}\| \overline{AE}.\end{align*}$
  ::考虑下ABC与AE的角角角角角角角角角角角角角角角角角角角角D的构造, 使DC'AE。

  播放段落

  Prove that $\begin{align*}\frac{EB}{BA}=\frac{EC}{CA}\end{align*}$ .
  ::证明EBBA=ECCA。

  	Statements	Reasons
  In $\begin{align*}\triangle DBC\end{align*}$ , $\begin{align*}AE \parallel DC\end{align*}$
  	$\begin{align*}\angle EAC\end{align*}$ $\begin{align*}\cong\end{align*}$ $\begin{align*}\angle DCA\end{align*}$	, $\begin{align*}\overline{DC} \parallel \overline{AE}\end{align*}$
  	$\begin{align*}\angle BAE\end{align*}$ $\begin{align*}\cong\end{align*}$ $\begin{align*}\angle BDC\end{align*}$	Corresponding angles, $\begin{align*}\overline{DC} \parallel \overline{AE}\end{align*}$
  	$\begin{align*}\angle BAE\end{align*}$ $\begin{align*}\cong\end{align*}$ $\begin{align*}\angle EAC\end{align*}$	Given:  $\begin{align*}\overline{AE}\end{align*}$ is the internal bisector of $\begin{align*}\angle BAC\end{align*}$
  	$\begin{align*}\angle BDC\end{align*}$ $\begin{align*}\cong\end{align*}$ $\begin{align*}\angle DCA\end{align*}$	Transitive property
  	$\begin{align*}\overline{AD} = \overline{CA}\end{align*}$	Sides opposite to equal angles of a triangle are equal.

  播放段落

  By the triangle proportionality theorem, $\begin{align*}\frac{EB}{EC}=\frac{BA}{AD}.\end{align*}$
  ::以三角比例定理,EBEC=BAAD。

  播放段落

  Multiply both sides of this proportion by $\begin{align*}\frac{EC}{BA}.\end{align*}$
  ::将这一比例的两面乘以欧洲央行局。

  播放段落

  $$\begin{align*}\frac{EB}{\cancel{EC}} \cdot \frac{\cancel{EC}}{BA} &=\frac{\cancel{BA}}{AD}\cdot \frac{EC}{\cancel{BA}} \\ \rightarrow \frac{EB}{BA} &=\frac{EC}{AD} \vphantom{\sum^X_X}\end{align*}$$
  ::EBEC ECBA=BAAD ECBABA=ECBABA ENBBA=ECDXX ECA=ECADXX ECBA=BAAD*EBA=EBEBA=ECBABA=ECBABA=ECBABA=ECDXXX ECBA=ECADXX ECA=ECADXX=ECADXXX ECBA=EBAD=EBEC ECECBABBA=BAD=BAD ECBA ECBABA EBA EBAEBBA=ECBA=ECBA ECBA=ECEBA=ECXXXX

  播放段落

  This proves the triangle angle bisector theorem which states that the angle bisector of one angle of a triangle divides the opposite side of the triangle into segments proportional to the lengths of the other two sides of the triangle .
  ::这证明了三角角对角的双角定理, 它表明三角角的一个角对角对角将三角角的对面分割成与三角角其他两边长度成正比的区段。

  ---

  播放段落

  Congruent Triangles Proof
  ::相容三角三角形校验

  播放段落

  Consider $\begin{align*}\triangle DAB\end{align*}$ and $\begin{align*}\triangle DCB\end{align*}$ with $\begin{align*}\overline{BD},\end{align*}$ the angle bisector of $\begin{align*}\angle ABC,\end{align*}$  where $\begin{align*}BA \perp AD\end{align*}$ and $\begin{align*}BC \perp DC\end{align*}$ .
  ::BAZAD 和 BCDC 的角角。

  播放段落

  Prove that $\begin{align*}\overline{AD} \cong \overline{DC}.\end{align*}$
  ::证明这一点是肯定的。

   

  	Statements	Reasons
  In $\begin{align*}\triangle DAB\end{align*}$ and $\begin{align*}\triangle DCB\end{align*}$ ,
  	$\begin{align*}\overrightarrow{BD}\end{align*}$ bisects $\begin{align*}\angle ABC\end{align*}$ , $\begin{align*}\overrightarrow{BA} \bot \overline{AD}\end{align*}$ , $\begin{align*}\overrightarrow{BC} \bot \overline{DC}\end{align*}$	Given
  	$\begin{align*}\angle ABD \cong \angle DBC\end{align*}$	Definition of an angle bisector
  	$\begin{align*}\angle DAB\end{align*}$ and $\begin{align*}\angle DCB\end{align*}$ are right angles	Definition of perpendicular lines
  	$\begin{align*}\angle DAB \cong \angle DCB\end{align*}$	All right angles are congruent
  	$\begin{align*}\overline{BD} \cong \overline{BD}\end{align*}$	Reflexive property
  	$\begin{align*}\triangle ABD \cong \triangle CBD\end{align*}$	AAS
  	$\begin{align*}\overline{AD} \cong \overline{DC}\end{align*}$

  ---

  播放段落

  Examples
  ::实例实例实例实例

  播放段落

  Example 1
  ::例1

  播放段落

  Can you find any similar triangles in the picture below?
  ::您在下面的图片中能找到相似的三角形吗 ?

  播放段落

  There are three triangles in this picture: $\begin{align*}\triangle BAC\end{align*}$ , $\begin{align*}\triangle BCD\end{align*}$ , $\begin{align*}\triangle CAD\end{align*}$ .
  ::此图中有三个三角形 : @BAC, @BCD, @CAD。

  播放段落
  • All three triangles are right triangles, so they have one set of congruent angles (the right angle ).
    ::所有三个三角都是右三角, 所以它们有一组相似的角度( 右角 ) 。
  播放段落
  • $\begin{align*}\triangle BAC\end{align*}$ and $\begin{align*}\triangle BCD\end{align*}$  additionally share $\begin{align*}\angle B\end{align*}$ , so $\begin{align*}\triangle BAC \thicksim \triangle BCD\end{align*}$ by AA $\begin{align*}\! \thicksim.\end{align*}$
    ::@BAC和BCD额外分享#B, 所以#BACBCD由AA__BCD分享。
  播放段落
  • $\begin{align*}\triangle BAC\end{align*}$ and $\begin{align*}\triangle CAD\end{align*}$  additionally share $\begin{align*}\angle A\end{align*}$ , so $\begin{align*}\triangle BAC\thicksim \triangle CAD\end{align*}$ by AA $\begin{align*}\thicksim\!.\end{align*}$
    ::@BAC和ZCAD也分享了AA,所以AAAA的BACCAD。

  播放段落

  By the transitive property, all three triangles must be similar to one another.
  ::根据过境财产,所有三个三角必须彼此相似。

  播放段落

  Example 2
  ::例2

  播放段落

  The large triangle above has sides $\begin{align*}a\end{align*}$ , $\begin{align*}b\end{align*}$ and $\begin{align*}c\end{align*}$ . Side $\begin{align*}c\end{align*}$ has been divided into two parts: $\begin{align*}y\end{align*}$ and $\begin{align*}c-y\end{align*}$ .  As proved in Example 1:   $\begin{align*}\triangle BAC,\end{align*}$   $\begin{align*}\triangle BCD,\end{align*}$   and $\begin{align*}\triangle CAD\end{align*}$   are similar triangles.
  ::上方的大三角形有a、b和c的侧面。 侧面 c 分为两部分: y 和 c-y。 如例1: QBAC、 QBCD 和 QCAD 是相似的三角形。

  播放段落

  Explain why $\begin{align*}\frac{a}{c}=\frac{c-y}{a}\end{align*}$ .
  ::解释为什么ac=c-ya。

  播放段落

  When triangles are similar, corresponding sides are proportional.
  ::当三角形相似时,对应的两边是成比例的。

  播放段落

  Since $\begin{align*}\triangle BAC \sim \triangle BCD\end{align*}$ , you know that  $\begin{align*}\frac{BC}{BA}\end{align*}$ $\begin{align*}=\end{align*}$ $\begin{align*}\frac{CD}{AC}\end{align*}$ $\begin{align*}=\end{align*}$ $\begin{align*}\frac{BD}{BC}\end{align*}$ .
  ::从BACBCD开始,你知道BBBA=CDAC=BDBC。

  播放段落

  The symbol $\begin{align*}\hat=\end{align*}$  is commonly used to mean 'corresponds to ':
  ::符号 通常指 “ 对应” :

  播放段落
  • $\begin{align*}a ~ \hat= ~ BC\end{align*}$
    ::a___________________________________________________________________________________________________________________
  播放段落
  • $\begin{align*}c ~ \hat= ~ BA\end{align*}$
    ::学 士 学 士 学 士
  播放段落
  • $\begin{align*}c-y ~ \hat= ~ BD\end{align*}$
    ::BD - BD - BD - BD - BD - BD - BD - BBD - BBD - BBD - BBD - BBD - BBD - BBD - BBD - BBD - BBD - BBD - BBD - BBD - BBD - BBD - BBD -BD - BBD -BD -BD -BD -BD -BD -BD -BD -BD -BD -BD -BD -BD -BD -BD -BD -BD -BD -BD -BD -BD -BD -BD -BD -BD

  播放段落

  M atch corresponding sides :
  ::匹配对应面 :

  播放段落

  $\begin{align*}\frac{BC}{BA} = \frac{BD}{BC} \longrightarrow \frac{a}{c} =\frac{c-y}{a} \vphantom{\sum^X_X}\end{align*}$
  ::BBBA=BDBDB=BDB=BDB=BC=C-YAX*X

  播放段落

  Example 3
  ::例3

  播放段落

  Explain why $\begin{align*}\frac{b}{c} = \frac{y}{b}.\end{align*}$
  ::解释为什么bc=yb。

  播放段落

  When triangles are similar, corresponding sides are proportional.
  ::当三角形相似时,对应的两边是成比例的。

  播放段落

  Since $\begin{align*}\triangle BAC \sim \triangle CAD\end{align*}$ , you know that  $\begin{align*}\frac{CA}{BA}\end{align*}$ $\begin{align*}=\end{align*}$ $\begin{align*}\frac{AD}{AC}\end{align*}$ $\begin{align*}=\end{align*}$ $\begin{align*}\frac{CD}{BC}\end{align*}$
  ::自从BACQCAD, 你知道CABA=ADAC=CDBC,CABA=ADA=CDBC。

  播放段落

  M atch corresponding sides :
  ::匹配对应面 :

  播放段落
  • $\begin{align*}b ~ \hat= ~ CA\end{align*}$  
    :b) 会计师协会
  播放段落
  • $\begin{align*}c ~ \hat= ~ BA\end{align*}$  
    ::学 士 学 士 学 士
  播放段落
  • $\begin{align*}y ~ \hat= ~ AD\end{align*}$  
    ::y = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =
  播放段落
  • $\begin{align*}b ~ \hat= ~ AC\end{align*}$  
    ::b 丙烷

  播放段落

  $\begin{align*}\frac{CA}{BA} = \frac{AD}{AC} \longrightarrow \frac{b}{c} =\frac{y}{b}\end{align*}$
  ::CABA=ADAC=ADAC=BC=yb=CABA=ADAC=ADAC=Bc=yb

  播放段落

  Example 4
  ::例4

  播放段落

  Use the results from Example 2 and Example 3 to show that $\begin{align*}a^2+b^2=c^2\end{align*}$ .
  ::使用例2和例3的结果来显示 a2+b2=c2。

  播放段落

  Cross multiply to rewrite each equation:
  ::交叉乘以重写每个方程式 :

  播放段落

  $\begin{align*}\frac{a}{c} &=\frac{c-y}{a}\longrightarrow a^2=c^2-cy \\ \frac{b}{c} &=\frac{y}{b}\longrightarrow b^2=cy \\\end{align*}$
  ::ac=c-yaa2=c2-cybc=ybb2=cyc =c-yaa2=c2-cybc=yb_b2=cyr

  播放段落

  Add the above two equations together:
  ::将以上两个方程加在一起:

  播放段落

  $\begin{align*}a^2+b^2 &=c^2-cy+cy\\ a^2+b^2 &=c^2 \end{align*}$
  ::a2+b2=c2 - cy+cya2+b2=c2 - Cy2 - Cy2+cya2+b2=c2

  播放段落

  Congratulations! Y ou have just proved using similar triangles.
  ::恭喜! 您刚刚证明使用相似的三角形 。

  Summary

  播放段落 Triangle Proportionality Theorem : A line parallel to one side of a triangle divides the other two sides of the triangle proportionally. ::三角比例定理:三角形对齐的一条线将三角形对面的另外两边成比例地分隔开来。 播放段落 Triangle Angle Bisector Theorem: The angle bisector of one angle of a triangle divides the opposite side of the triangle into segments proportional to the lengths of the other two sides of the triangle. Pythagorean Theorem: For a right triangle with legs $\begin{align*}a\end{align*}$  and $\begin{align*}b\end{align*}$  and hypotenuse $\begin{align*}c\end{align*}$  : $\begin{align*}a^2+b^2=c^2.\end{align*}$   ::三角三角形双扇形定理:三角形角的一个角角角两角区段将三角形对面的三角形对面分割成与三角形其他两边长度成正比的区段。Pytagoren 定理:右三角形,腿为a和b,下角为c:a2+b2=c2。

  ---

  播放段落

  Reviews
  ::审查

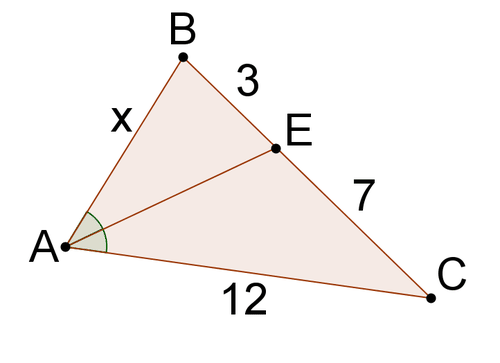
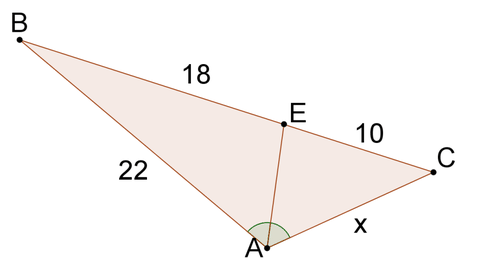
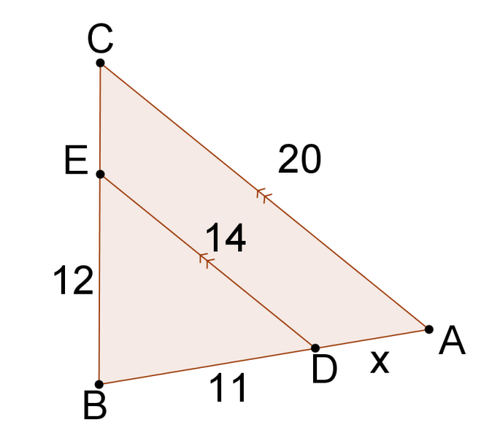
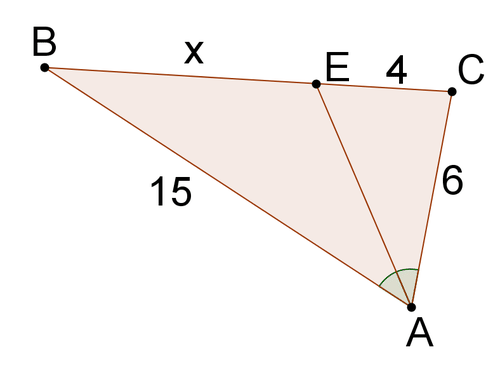
  播放段落

  Solve for $\begin{align*}x\end{align*}$ in each problem.
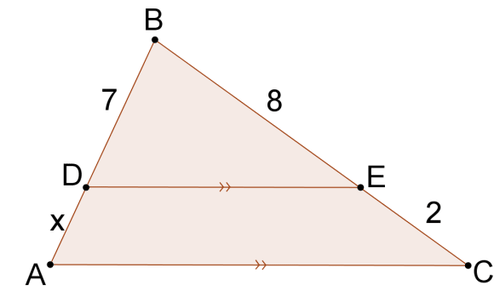
  ::解决每个问题中的 x。

  1.

  

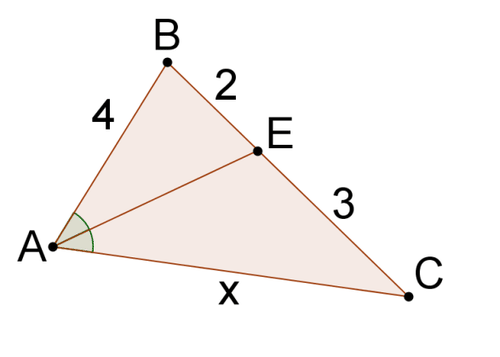
  2.

  

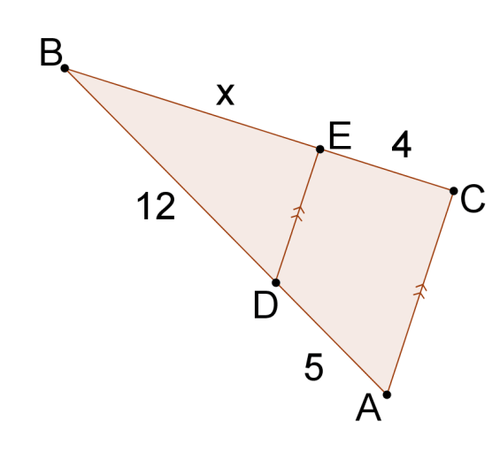
  3.

  

  4.

  

  5.

  

  6.

  

  7 .

  

  播放段落

  Use the picture below for #8-#10.
  ::使用下面的图片为 # 8 -# 10 显示 。

  

  播放段落

  8. Solve for $\begin{align*}x\end{align*}$ .
  ::8. 解决x.

  播放段落

  9. Solve for $\begin{align*}z\end{align*}$ .
  ::9. 解决z.

  播放段落

  10. Solve for $\begin{align*}y\end{align*}$ .
  ::10. 解决y.

  播放段落

  Use the picture below for #11-#13.
  ::用下面的图片显示 #11 -#13。

  

  播放段落

  11. Assume that $\begin{align*}\frac{b}{a}=\frac{d}{c}\end{align*}$ . Use algebra to show that $\begin{align*}\frac{b+a}{a}=\frac{d+c}{c}\end{align*}$ .
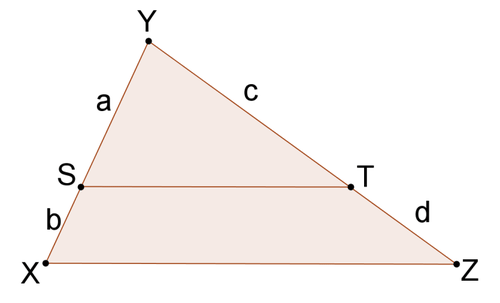
  ::11. 假设Ba=dc. 使用代数显示b+aa=d+cc。

  播放段落

  12. Prove that $\begin{align*}\triangle YST \thicksim \triangle YXZ\end{align*}$
  ::12. 证明`YST'YXZ

  播放段落

  13. Prove that $\begin{align*}\overline{ST}\| \overline{XZ}\end{align*}$
  ::13. 证明那不是XZ

  播放段落

  14. Prove that a segment that connects the midpoints of two sides of a triangle will be parallel to the third side of the triangle.
  ::14. 证明连接三角形两侧中点的段段将与三角形第三侧平行。

  播放段落

  15. Prove the Pythagorean Theorem using the picture below.
  ::15. 利用以下图象来证明毕达哥里安理论论。

  

  播放段落

  16. Refer to the diagram below to prove the triangle angle bisector theorem by a slightly different method.
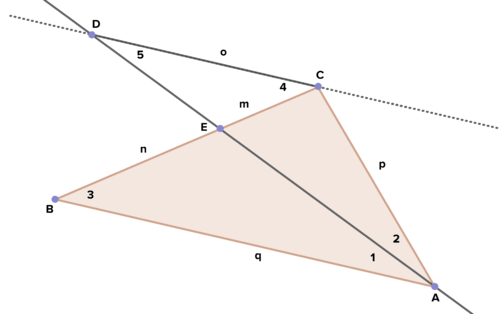
  ::16. 参考下图以略微不同的方法证明三角角对角定理。

  播放段落

  Given: $\begin{align*}\angle 1 \cong \angle 2\end{align*}$ ; $\begin{align*}\overline{DC} \parallel \overline {BA}\end{align*}$ by construction
  ::面积:%1 @%2;通过建筑开发

  播放段落

  Prove: $\begin{align*}\frac{m}{n}=\frac{p}{q}\end{align*}$
  ::证明: mn=pq

  播放段落

  Here are some questions to guide you in your proof:
  ::以下是一些问题,以证明你的证据:

  播放段落

  a. It's given that  $\begin{align*}\angle 1 \cong \angle 2\end{align*}$ . Is it also true that $\begin{align*}\angle 1 \cong \angle 5\end{align*}$ ?
  :笑声) (掌声) (掌声) (掌声) (掌声) (掌声) (掌声) (掌声) (掌声) (掌声) (掌声) (掌声) (掌声) (掌声) (掌声) (掌声) (掌声) (掌声) (掌声) (掌声) (掌声) (掌声) (掌声) (掌声) (掌声) (掌声) (掌声) (掌声) (掌声) (掌声) (掌声) (掌声) (掌声) (掌声) (掌声) (掌声) (掌声) (掌) (掌) (掌声) (掌声) (掌声) (掌声) (掌声) (掌声) (掌声) (掌声) (掌声) (掌声) (掌声) (掌声) (掌声) (掌声) (掌声) (掌声) (掌) (掌声) (掌声) (掌声) (掌声)(掌)(掌声)(掌声)(掌)(掌)(掌)(掌)(掌)(掌)(掌)(掌)(掌)(掌)(掌声)(掌)(掌)(掌)(掌)(掌)(掌)(掌)(掌)是)是)是)是)是)是)(掌)(掌)(掌)(掌)(掌)(掌)(掌)(掌)(掌)(掌)(掌)(掌)(掌)(掌)(掌)(掌)(掌)(掌)(掌)(掌)(掌)(掌)(掌)是)(掌)(掌)(掌)是)是)(掌)

  播放段落

  b. Can you conclude $\begin{align*}\triangle DEC\end{align*}$  and $\begin{align*}\triangle AEB\end{align*}$  are similar? If so how?
  :b) 你能得出“DEC”和“AEB”相似的结论吗?

  播放段落

  c. Look again at $\begin{align*}\triangle DEC\end{align*}$  and $\begin{align*}\triangle AEB.\end{align*}$  Can you determine which corresponding sides are proportional?
  :c) 再看看“DEC”和“AEB”。你能确定哪些对应方是比例的吗?

  播放段落

  d. What type of triangle is $\begin{align*}\triangle DCA\end{align*}$ ?
  ::d. QADCA是何种三角形?

  播放段落

  e. Use the information you found from the above questions to prove  $\begin{align*}\frac{m}{n}=\frac{p}{q}.\end{align*}$
  ::e. 使用您从上述问题中找到的信息来证明 mn=pq 。

  

  播放段落

  Review (Answers)
  ::审查(答复)

  播放段落

  Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
  ::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键 。