7.5 寻找三角区域线-interactive

Section outline

• Select section General

  Collapse Expand

  General

  Collapse all Expand all

  • Select activity 新闻通告

    

    新闻通告 Forum
• Select section 寻找三角区域

  Collapse Expand

  寻找三角区域

  播放段落

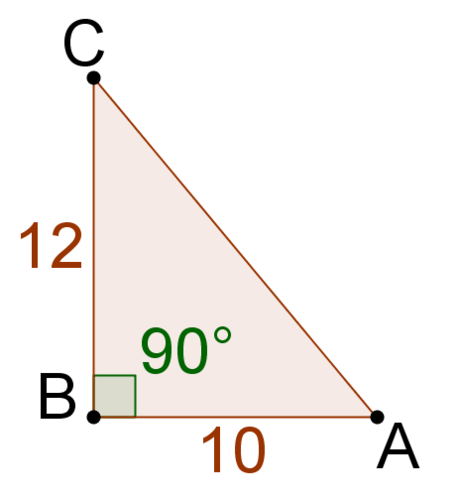
  T he most common  way to find the area of a triangle is by calculating $\begin{align*}\frac{1}{2}bh\end{align*}$ . However, this formula only works when you know or can determine the base and the height of a triangle. Sometimes the height is not immediately apparent. 
  ::找到三角形区域最常用的方法是计算 12bh。 但是, 这个公式只有在您知道或能够确定三角形的基数和高度时才有效。 有时, 高度并不立即明显 。

  播放段落

  For instance, suppose  you wanted to find the area of the following triangle:
  ::例如,假设你想找到以下三角形的区域:

  

  播放段落

  The two given sides are not the base and the height. You need to determine the height in order to use the area formula.
  ::给定的两边不是基点和高度。 您需要确定高度才能使用区域公式 。

  ---

  播放段落

  Determine the Height of a Non-Right Triangle
  ::确定非右三角的高度

  播放段落

  T he altitude of $\begin{align*}\triangle ABC\end{align*}$ from vertex  $\begin{align*}A\end{align*}$ has been drawn below.
  ::从顶端A的 QABC 高度绘制如下。

  播放段落

  Write an equation that relates $\begin{align*}h\end{align*}$  to  $\begin{align*}34^{\text{o}}\end{align*}$ and 7.
  ::写一个和34oand 7有关的方程

  播放段落

  Notice that two right triangles have been formed. This means you can use the trigonometric ratios to relate the sides. $\begin{align*}h\end{align*}$ is opposite to the $\begin{align*}34^{\text{o}}\end{align*}$  angle and 7 is the length of the hypotenuse of the right triangle . This is the sine relationship.
  ::注意两个右三角已经形成。 这意味着您可以使用三角比连接侧面。 h 与34o 角度相对, 7 是右三角的下限长度。 这是正弦关系 。

  播放段落

  $$\begin{align*}\sin 34^{\text{o}}& =\frac{AD}{AB} = \frac{h}{7}\\ \sin 34^{\text{o}}& = \frac{h}{7}\\ h&=7 \sin34^{\text{o}}\\ h&= 7 (0.5592)\\ h&= 3.9144\end{align*}$$
  ::=h7sin=h7h=h7h=7sin=34oh=7(0.5592)h=3.9144

  播放段落

  The height $\begin{align*}h\end{align*}$  is 3.9144 units
  ::高度为3.9144个单位

  ---

  播放段落

  Generalizing the Area Formula for Non-Right Triangles
  ::普及非右三角区域公式

  播放段落

  Now you can solve for area, using the common formula. Note that, f or the given height, $\begin{align*}\overline{BC}\end{align*}$ is the base .
  ::现在您可以用通用公式解决区域问题。 请注意, 对于给定的高度, BC 是基数 。

   

  播放段落

  Notice the calculation: $\begin{align*}A =\frac{1}{2} (12) (7) (\sin 34^{\text{o}}).\end{align*}$
  ::通知计算:A=12(12)(7)(sin34o)。

  播放段落

  The area is  half the product of the two sides and the sine of the included angle.
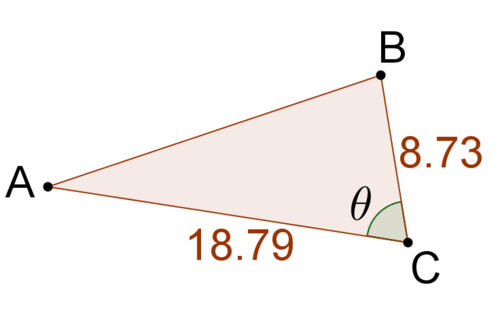
  ::区域是两侧一半的产物,是包含角的正弦。

  播放段落

  Now consider the general triangle below:
  ::现在考虑下面的一般三角形 :

  

  播放段落

  If you know $\begin{align*}\angle B\end{align*}$ , the formula to determine the area will be $\begin{align*}\text{Area} = \frac{1}{2} (a)(c) \sin B\end{align*}$ .
  ::如果您知道 {B},确定区域的公式将是区域=12(a)(c)sinB。

  播放段落

  If you know $\begin{align*}\angle C\end{align*}$ , the area formula  will be   $\begin{align*}\text{Area}=\frac{1}{2} (a)(b) \sin C\end{align*}$ .
  
  ::如果您知道 C, 区域公式将是区域=12(a)(b)sinC。

  ---

  播放段落

  CK-12 PLIX Interactive
  ::CK-12 PLIX 交互式互动

  播放段落

  Area Formula for Non-Right Triangles
  ::非右三角区公式

  ---

  播放段落

  Finding the Area Given the Obtuse Angle
  ::发现"区域"时的刻刻度

  播放段落

  Consider the triangle below. To find the area of the triangle, you need to find the equation to determine the value of $\begin{align*}h\end{align*}$ .
  ::考虑下方的三角形。要找到三角形的区域,您需要找到方程式来确定 h 的值。

  播放段落

  Remember that the interior and the exterior angles at the vertex must sum to $\begin{align*}180^{\text{o}}\!,\end{align*}$  so the measure of the exterior angle of the triangle at vertex $\begin{align*}B\end{align*}$ is $\begin{align*}55^{\text{o}}( 180^{\text{o}} - 125^{\text{o}}).\end{align*}$
  ::记住顶端的内外角必须等于 180o, 所以顶端 B 三角形外部角的测量值是 55o( 180o-125o) 。

  播放段落

  Now, consider the right triangle with the length of the side opposite $\begin{align*}\angle B\end{align*}$ as $\begin{align*}h\end{align*}$ and the hypotenuse as 7.  You can use the sine function to determine $\begin{align*}h\end{align*}$ .
  ::现在,将右三角形与对面QB的侧边长度视为h,将下限视为7。 您可以使用正弦函数来确定h。

  播放段落

  $\begin{align*}\sin 55^{\text{o}} &= \frac{h}{7}\\ h &= 7 \sin 55^{\text{o}}\\\end{align*}$
  ::555o=h7h=7sin55o

  播放段落

  For the height that has been drawn, $\begin{align*}\overline{BC}\end{align*}$ is the base. Now you can find the area with the common formula. 
  ::对于所绘制的高度, BC 是基数。 现在您可以用共同公式找到区域 。

  播放段落

  In general, if your given angle is obtuse, you can use the angle supplementary to your given angle in your area calculation.
  ::一般而言,如果给定角度是模糊的,您可以在区域计算中使用给定角度的补充角度。

  ---

  播放段落

  Area of a Triangle
  ::三角三角区域区域

  播放段落

  Select the angle and drag the vertex to reshape the triangle. The formula shown will recalculate the area of the triangle.
  ::选择角并拖动顶点以重塑三角形。显示的公式将重新计算三角形的区域。

  ---

  ---

  播放段落

  Examples
  ::实例实例实例实例

  播放段落

  Example 1
  ::例1

  播放段落

  You have previously learned that the area of a triangle is $\begin{align*}A=\frac{1}{2}bh\end{align*}$ where $\begin{align*}b\end{align*}$ is a base of the triangle and $\begin{align*}h\end{align*}$ is the corresponding height. Why is it helpful to have another formula for calculating the area of a triangle?
  ::您以前已经知道三角形的区域是 A=12bh, b 是三角形的底部, h 是相应的高度。 为什么使用另一个公式来计算三角形的区域会有帮助 ?

  播放段落

  Often you only know the sides and angles of a triangle and not the height. $\begin{align*}A=\frac{1}{2} (a)(b) \sin C\end{align*}$ allows you to quickly find the area of acute or obtuse triangles when given two sides and an included angle.
  ::通常您只知道三角形的侧面和角度, 而不是高度。 A=12(a)(b)(sin) =C 允许您在给定两边和一个包含角度时快速找到急性或隐形三角形的区域 。

  播放段落

  Example 2
  ::例2

  播放段落

  Find the area of the triangle.
  ::找到三角形的区域 。

  

  播放段落

  The $\begin{align*}65^{\text{o}}\end{align*}$ angle is the included angle to the two given sides of length 7 and 10.
  ::65oangle是7和10长度两侧的角。

  播放段落

  $\begin{align*}\text{Area}& = \frac{1}{2}(b)(c) \sin A \\ A &= \frac{1}{2} (7)(10) \sin 65^{\text{o}}\\ A & \approx 31.72 \ \text{units}^2\end{align*}$
  ::区域=12(b)(c)sinA=12(7)(10)sin65oA31.72单位2

  播放段落

  Example 3
  ::例3

  播放段落

  Find the area of the triangle.
  ::找到三角形的区域 。

  

  播放段落

  The sine ratio is actually a function that takes any angle measure as an input (not just angles between $\begin{align*}0^{\text{o}}\end{align*}$ and $\begin{align*}90^{\text{o}}\end{align*}$ ). One property of the sine function is that the sine of supplementary angles will always be equal. Therefore, when finding the area of a triangle given an obtuse angle, you can use the obtuse angle in your calculation instead of the acute supplementary angle and your answer will be the same. Note: You will study the sine function in much more detail in future courses!
  ::正弦比实际上是一个函数,它将任何角度的度量作为输入(而不仅仅是0和90o之间的角)。正弦函数的一个属性是补充角度的正弦永远是相等的。因此,在找到三角形区域给定了一个斜角时,您可以在计算时使用隐性角,而不是急性补充角度,答案是一样的。注意:在未来的课程中,您将更详细地研究正弦函数。

  播放段落

  Notice that the given angle is obtuse. Draw the altitude from vertex $\begin{align*}C\end{align*}$ so that it intersects the extension of $\begin{align*}\overline{AB}\end{align*}$ at point $\begin{align*}D\end{align*}$ . The exterior angle at $\begin{align*}\angle A\end{align*}$ is $\begin{align*}30^{\text{o}}.\end{align*}$
  ::注意给定角度是模糊的。 从顶部 C 绘制高度, 使其在 D 点交叉 AB 的扩展。 A 的外部角是 30 o 。

  播放段落

  Use the new area formula with the $\begin{align*}30^{\text{o}}\end{align*}$ angle.
  ::使用带有 30oangle 的新区域公式 。

  播放段落

  $\begin{align*}\text{Area} & = \frac{1}{2}(b)(c) \sin A \\ A &= \frac{1}{2} (9)(15) \sin 30^{\text{o}}\\ A &= 33.75 \ \text{units}^2\end{align*}$
  ::区域=12(b)(c)sinA=12(9)9(15)sin30oA=33.75单位2

  播放段落

  Example 4
  ::例4

  播放段落

  Find the area of the triangle from Example #3 using the obtuse angle in your calculations. What do you notice?
  ::从例3中查找三角形的区域,在计算时使用斜角。你注意到什么?

  播放段落

  Use the area formula as in Example #3. Instead of using $\begin{align*}30^{\text{o}}\end{align*}$ , use $\begin{align*}150^{\text{o}}\end{align*}$ .
  ::使用例3中的面积公式。 使用面积公式, 而不是使用 30o, 使用 150o 。

  播放段落

  $\begin{align*}A &= \frac{1}{2} (9)(15) \sin 150^{\text{o}}\\ A &= 33.75 \ \text{units}^2\end{align*}$
  ::A=12(9)(15sin=150oA=33.75单位)2

  播放段落

  The result is the same:  $\begin{align*}\sin 30^{\text{o}}=0.5\end{align*}$ and $\begin{align*}\sin 150^{\text{o}}=0.5\end{align*}$ .
  ::结果是一样的:sin30o=0.5和sin150o=0.5。

  播放段落

  This means that regardless of whether the given angle is acute or obtuse, you can always find the area of a triangle by finding the half the product of two sides and the sine of their included angle:
  ::这意味着,无论给定角是尖角还是斜角,您总能找到三角形的面积,方法是找到两边的一半产物及其包括角的正弦:

  播放段落

  For all triangles: $\begin{align*}A=\frac{1}{2} (a)(b) \sin C\end{align*}$
  ::对于所有三角形 : A=12(a)(b) sinC

  Summary

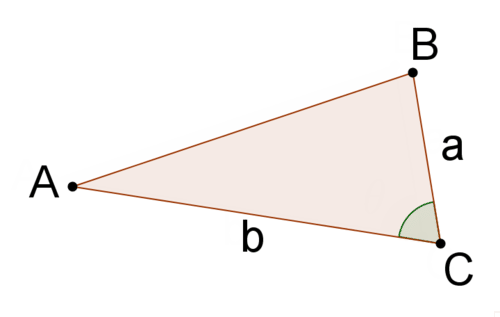
  播放段落 Given a triangle ::给定三角形 播放段落 If you know $\begin{align*}\angle B,\end{align*}$  the formula to determine the area will be $\begin{align*}A=\frac12(a)(c)\sin B.\end{align*}$   ::如果您知道 {B},确定区域的公式将是 A=12(a)(c)sinB。 播放段落 If you know $\begin{align*}\angle C,\end{align*}$  the formula to determine the area will be $\begin{align*}A=\frac12(a)(b)\sin C.\end{align*}$   播放段落 When solving for the area of an obtuse triangle, use the exterior angle. ::当解决隐形三角形区域时,请使用外部角度。 ::如果您知道 C, 确定区域的公式将是 A=12(a)(b)sinC。 当为隐形三角形区域解析时, 请使用外部角度 。

  ---

  播放段落

  Review
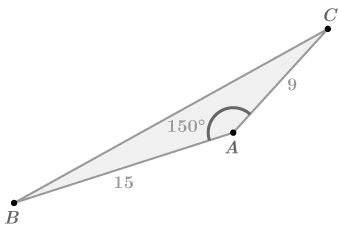
  ::审查审查审查审查

  播放段落

  Find the area of each triangle.
  ::找到每个三角形的区域 。

  1.

  

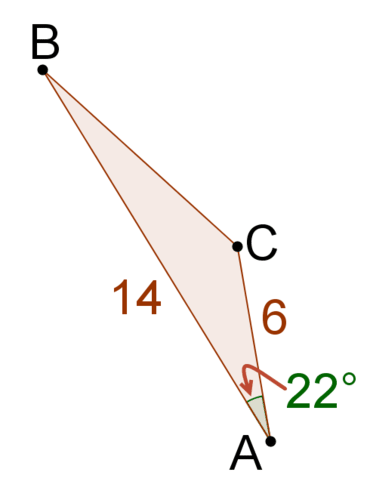
  2.

  

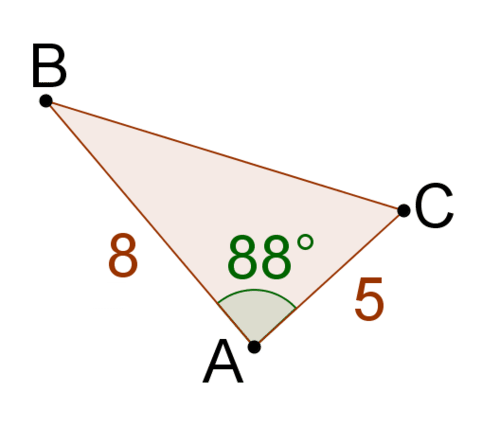
  3.

  

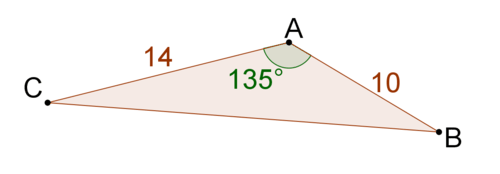
  4.

  

  播放段落

  5. Explain why the following triangle has the same area as the triangle in #4.
  ::5. 解释为何以下三角在#4中具有与三角相同的区域。

  

  播放段落

  Find the area of each triangle.
  ::找到每个三角形的区域 。

  6.

  

  7.

  

  8.

  

  播放段落

  9. Use your calculator to find $\begin{align*}\sin 90^{\text{o}}.\end{align*}$
  ::9. 利用计算器找到sin90o。

  播放段落

  10. Find the area of the triangle below in two ways. First, use the formula $\begin{align*}A=\frac{1}{2} bh\end{align*}$ . Then, use the new formula from this concept. What do you notice?
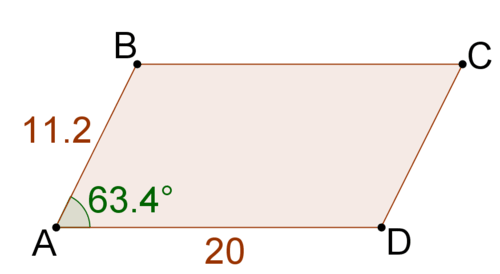
  ::10. 以两种方式查找下方三角形的区域。首先,使用公式A=12bh。然后,使用这个概念中的新公式。你注意到什么?

  

  播放段落

  11. Find the area of the parallelogram:
  ::11. 查找平行图的区域:

  

  播放段落

  12. Use your work from #11 to help you to describe a general method for calculating the area of a parallelogram given its sides and angles.
  ::12. 利用从 #11 开始的工作来帮助您描述一个根据侧面和角度计算平行图的区域的一般方法。

  播放段落

  13. The area of the triangle below is $\begin{align*}78 ~ \text{units}^2.\end{align*}$  Find the measure of $\begin{align*}\theta\end{align*}$ rounded to the nearest degree.
  ::13. 下面三角形的面积为78个单位2。 查找 `x'四舍五入到最接近的度量。

  

  播放段落

  14. Use the triangle below to explain where the area formula $\begin{align*}A=\frac{1}{2} ab \sin C\end{align*}$ comes from.
  ::14. 使用下面的三角形来解释A=12absinC区域公式的来源。

  

  播放段落

  15. Why does the area formula $\begin{align*}A=\frac{1}{2} ab \sin C\end{align*}$ work even if $\begin{align*}\angle C\end{align*}$ is obtuse?
  ::15. 为什么A=12absinC区域公式工作,即使C是模糊的呢?

  播放段落

  16. Consider a right triangle with legs of length 3 and 4. Find the area using two different formulas. Is the result the same? Why or why not?
  ::16. 考虑一个右三角形,右三角形的长度为3和4。用两种不同的公式查找区域,结果相同吗?为什么或为什么没有?

  播放段落

  17. Assume the triangle below is a right triangle with angle C having a measure of $\begin{align*}{90}^{\circ}.\end{align*}$ Use the formula learned in this lesson to write the area two different ways. Are these two results equal? Set them equal to each other and simplify as much as possible, so that the result shows two equivalent fractions. Create a problem that can be solved with this new formula.
  ::17. 假设下面的三角形是一个右三角形,角C的度量为 90\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\可以\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\

  

  播放段落

  18. For this problem, keep in mind that the sine of the supplement of an obtuse angle  $\begin{align*}\theta\end{align*}$ is the same as the sine of $\begin{align*}{180}^{\circ}-\theta\end{align*}$ . Create two different triangles for which two sides are the same, the angle between them $\begin{align*}\theta\end{align*}$  is obtuse and  such that the areas are the same.
  ::18. 对于这个问题,要记住,一个隐蔽角度的补角的必备条件与180°的正备条件相同。 创造两个不同的三角,两边是相同的,两边之间的角是模糊的,区域是相同的。

  播放段落

  Review (Answers)
  ::审查(答复)

  播放段落

  Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
  ::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键 。