7.6 锡奈法-interactive

Section outline

• Select section General

  Collapse Expand

  General

  Collapse all Expand all

  • Select activity 新闻通告

    

    新闻通告 Forum
• Select section Sines法律

  Collapse Expand

  Sines法律

  播放段落

  Consider $\begin{align*}\triangle ABC\end{align*}$ given below. The smallest angle is $\begin{align*}\angle A\end{align*}$ and it opens up to create the shortest side $\begin{align*}BC\end{align*}$ . The largest angle is $\begin{align*}\angle C\end{align*}$ and it opens up to create the longest side $\begin{align*}AB.\end{align*}$
  ::考虑下面给出的 ABC 。 最小的角是 A , 它打开以创建最短的 BC 边。 最大的角是 C , 它打开以创建最长的 AB 边 。

  播放段落

  C lick the small blue arrow next to the image below and drag the orange vertices to reshape triangle $\begin{align*}ABC.\end{align*}$  Observe that the shortest side is always opposite the smallest interior angle and the longest side is always opposite the largest interior angle.
  ::单击下方图像旁边的小蓝箭头,拖动橙色顶部以重塑三角 ABC 。注意最短的一面总是对最小的内角,最长的一面总是对最大的内角。

  播放段落

  Clearly, angles and opposite sides within triangles are connected. In fact, the Law of Sines states that the ratio between the sine of an angle and the side opposite the angle is constant for each of the three angle/side pairs within a triangle.
  ::显然,三角形内的角度和对面是相连的。 事实上,Sines法则规定角的正弦与角对面的边之间的比例对三角形内的三个角度/对边的对等都是不变的。

  播放段落

  Law of Sines: $\begin{align*}\frac{\sin A}{a}=\frac{\sin B}{b}=\frac{\sin C}{c}\end{align*}$
  ::Sines法律:SinAa=sinBb=sinCc

    播放段落

  One way to find the area of a non-right triangle is to divide the non-right triangle into two right triangles and calculate the altitude, so you can use the common $\begin{align*}\tfrac{1}{2}bh\end{align*}$  formula.
  ::找到非右三角形区域的一种方法是将非右三角形分为两个右三角形,计算高度,以便使用共同的 12bh 公式。

  播放段落

  With the Law of Sines, you can directly find missing sides and angles in any type of triangle.
  ::以辛尼定律,你可以在任何三角形中 直接找到缺失的侧面和角度。

  ---

  播放段落

  Proving the Law of Sines
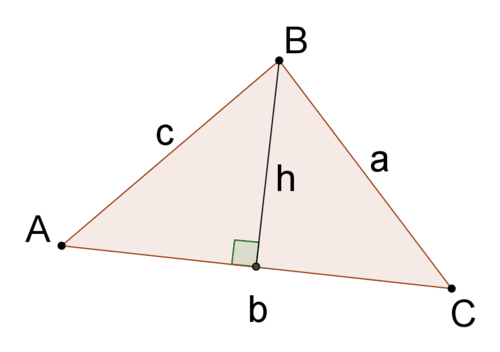
  ::证明Sines定律

  播放段落

  1. Consider $\begin{align*}\triangle ABC\end{align*}$ below.
  ::1. 以下考虑ABC。

  播放段落

  The  altitude , $\begin{align*}h,\end{align*}$  from vertex $\begin{align*}B\end{align*}$  intersects $\begin{align*}\overline{AC}\end{align*}$ to divide $\begin{align*}\triangle ABC\end{align*}$ into two right triangles .
  ::高度,h,从脊椎B交叉 AC 将 ABC 分为两个右三角。

  播放段落

  Find two equations for the length of the altitude.
  ::查找两个方程式以显示高度长度。

  播放段落
  1. Consider the right triangle, $\begin{align*}\triangle ABD\end{align*}$ with hypotenuse of length $\begin{align*}c\end{align*}$ . $\begin{align*}h\end{align*}$ is opposite $\begin{align*}\angle A\end{align*}$ in this triangle. With an opposite side and hypotenuse you can use the sine ratio.
     ::考虑右三角形,在此三角形中, XAD 的长度为 c. h 的 ABD 与 QA 的对面。如果右三角形的对面和对面,您可以使用正弦比。

  播放段落

  $$\begin{align*}\sin A &= \frac{h}{c}\\ h &= c \sin A\end{align*}$$
  ::罪A=hch=csinA 罪A=hch=csinA 罪A=hch=csinA

  播放段落
  2. Now consider the right triangle, $\begin{align*}\triangle BCD\end{align*}$ with hypotenuse of length $\begin{align*}a\end{align*}$ . $\begin{align*}h\end{align*}$ is opposite $\begin{align*}\angle C\end{align*}$ in this triangle. Again, w ith an opposite side and hypotenuse you can use the sine ratio.
     ::现在考虑一下右三角形, 在这个三角形中, QQBCD 的长度为 a. h 的下限是对的 QC 。 另外, 如果右侧和下限是对的, 您可以使用正弦比例 。

  播放段落

  $$\begin{align*}\sin C &= \frac{h}{a}\\ h &= a \sin C\end{align*}$$
  ::C=hah=asinC 罪行

  播放段落

  You have now found two equations for $\begin{align*}h.\end{align*}$
  ::您现在找到了 H的两个方程式 。

  播放段落

  You know now that  $\begin{align*}h=c \sin A,\end{align*}$ and $\begin{align*}h=a \sin C.\end{align*}$  This means that $\begin{align*}c \sin A=a \sin C.\end{align*}$
  ::现在你知道h=csinA,和h=asinC。 这意味着csinA=sinC。

  播放段落

  Divide both sides by $\begin{align*}ac\end{align*}$   to  see the Law of Sines:
  ::双方以ac除以ac,以观察Sines法则:

  播放段落

  $$\begin{align*}c \sin A &= a \sin C\\ \frac{c \sin A}{ac} &= \frac{a \sin C}{ac}\vphantom{\sum^X_X}\\ \frac{\sin A}{a} &= \frac{\sin C}{c}\end{align*}$$
  ::csinA = asinCcsinAac = asinCasinCac XXXsinAa = sinCc = asinAa = asinAa = asinCsinAa = asinAa = asinCsinAac = asinCc

  播放段落

  $\begin{align*}A\end{align*}$ and $\begin{align*}C\end{align*}$ were two random angles in the original triangle. This proves that in general, within any triangle the ratio of the sine of an angle to its opposite side is constant.
  ::A 和 C 是原始三角形中两个随机角度。 这证明在任何三角形中, 角的正弦与角对面的正弦比例是恒定的 。

  ---

  播放段落

  Using the Law of Sines to Find Missing Sides
  ::利用Sines法律寻找失踪的侧面

  播放段落

  Use the Law of Sines to find $\begin{align*}BC\end{align*}$ and $\begin{align*}AC\end{align*}$ . 
  ::使用Sines法寻找 BC和AC。

  播放段落

  Look for an angle and side pair whose measurements are both given. $\begin{align*}m \angle C=64^\circ\end{align*}$ , and its opposite side is $\begin{align*}AB=12\end{align*}$ . Next, set up an equation using the two known measurements as one of the ratios in the Law of Sines. Make sure to match angles with opposite sides.
  ::查找一个角度和侧边对, 其测量结果都给出了 mC=64, 其对面是 AB=12。 下一步, 设置一个方程式, 使用两种已知测量结果作为辛尼定律中的比例之一 。 确保角度与对面匹配 。

  播放段落

  Solve for $\begin{align*}BC\end{align*}$ :
  ::为 BC 解决 :

  播放段落

  Solve for $\begin{align*}AC\end{align*}$ :
  ::用于空调的解决方案 :

  ---

  播放段落

  CK-12 PLIX Interactive
  ::CK-12 PLIX 交互式互动

  播放段落

  Angle-Angle-Side Triangles
  ::角度- 角度- 侧边三角形

  ---

  播放段落

  Examples
  ::实例实例实例实例

  播放段落

  Example 1
  ::例1

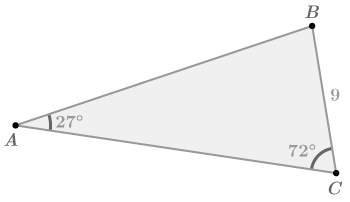
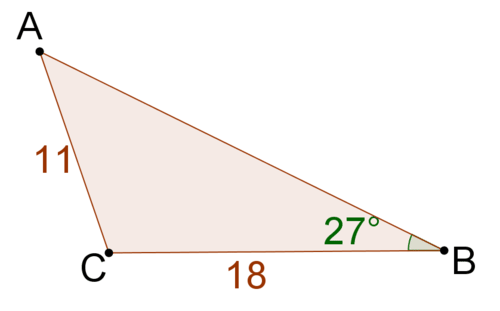
  播放段落

  In the triangle below,  find $\begin{align*}AB\end{align*}$
  ::在下方三角形中,请找到AB

  

  播放段落

  To find $\begin{align*}AB,\end{align*}$  use the Law of Sines. Match angles with opposite sides.
  ::要找到AB, 使用Sines定律, 匹配角度与对面 。

  播放段落

  $$\begin{align*}\frac{\sin A}{a} & = \frac{\sin C}{c} \\ \frac{\sin 27^{\text{o}}}{9} &= \frac{\sin 72^{\text{o}}}{AB}\vphantom{\sum^X}\\ AB &= \frac{9 \cdot \sin 72^{\text{o}}}{\sin 27^\circ}\vphantom{\sum^X_X}\\ AB & \approx 18.85\end{align*}$$
  ::一九九九年九月九日 一九九九年一九年二月二一日二十七日一九八八八年八月八日

  播放段落

  Example 2
  ::例2

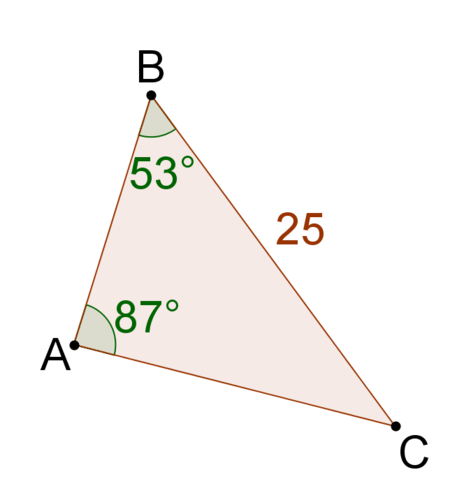
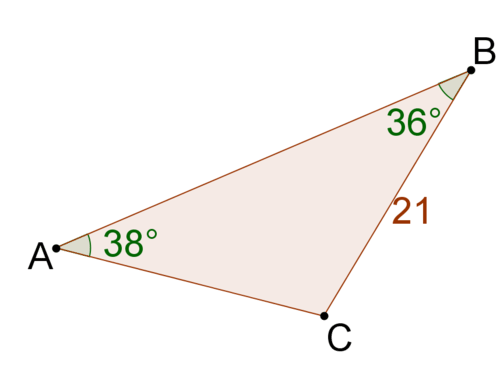
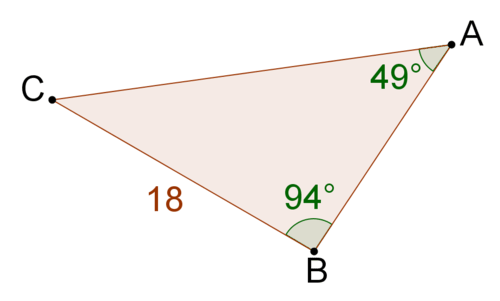
  播放段落

  The triangle below is drawn to scale. Use the Law of Sines to solve for the measure of angle $\begin{align*}B.\end{align*}$
  ::下面的三角形被拉到比例。 使用 Sines 法则来解析角度 B 的测量 。

  播放段落
  1. Does your answer support the appearance of the image ?
     ::您的回答是否支持图像的外观 ?
  播放段落
  2. Why not?
     ::为什么不呢?

  播放段落
  1. In the image of the triangle, $\begin{align*}\angle B\end{align*}$   appears  to clearly be an obtuse angle.
     ::在三角形的图像中, @B显然是一个模糊角度。

  播放段落

  Match angles with opposite sides.
  ::将角度与对立角度匹配 。

  播放段落

  $$\begin{align*}\frac{\sin A}{a} & = \frac{\sin B}{b}\\ \frac{\sin 36^{\text{o}}}{14} &= \frac{\sin B}{22}\vphantom{\sum^X_X}\\ \sin B &= \frac{22 \cdot \sin 36^{\text{o}}}{14}\\ m \angle B &= \sin^{\text{-}1} \left(\frac{22 \cdot \sin 36^{\text{o}}}{14}\right)\vphantom{\sum^X_X}\\ m \angle B & \approx 67.5^{\text{o}}\end{align*}$$
  ::SinAa=sinBbsin36o14=sinB22XXXsinB=22sin36o14m_B=sin-1(22_sin36o14)X_Xm_B\_B\#67.5o

  播放段落

  Determining that angle $\begin{align*}B\end{align*}$  is approximately 67.5 degrees doesn't match the image, because  $\begin{align*}B\end{align*}$  in the image clearly appears to be obtuse (therefore greater than  $\begin{align*}90^{\text{o}}\!\end{align*}$ ).
  ::确定角B约67.5度与图像不匹配,因为图像中的角B显然明显模糊(因此大于90o)。

  播放段落
  2. Recall that SSA was not a criterion for triangle congruence. This was because two non-congruent triangles could have the same "side-side-angle" pattern.
     ::回顾特别服务协定不是三角一致性的标准。 这是因为两个非三角关系可能具有相同的“ 侧边形” 模式。

  播放段落

  What does this have to do with the fact that the calculated angle doesn't match the scale figure ?
  ::这与计算角度与比额表数字不符这一事实有什么关系?

  播放段落

  There are two triangles that fit the given criteria ( angle measures have been slightly rounded):
  ::有两个三角形符合特定标准(矩形措施已略微四舍五入):

    播放段落

  The two possible measures of $\begin{align*}\angle B\end{align*}$ are supplementary $\begin{align*}(112^\circ+68^\circ=180^\circ)\end{align*}$ . Also note that, like all supplementary angle pairs, the values are equal:  $\begin{align*}\sin 112^{\text{o}}=0.927=\sin 68^{\text{o}}\!.\end{align*}$
  ::B的两种可能衡量标准是补充的(11268180)。 另请注意,与所有补充角度对一样,数值是相等的:sin112o=0.927=sin68o。

  播放段落

  The inverse sine function on your calculator will only produce angles between $\begin{align*}0^\circ\end{align*}$ and $\begin{align*}90^{\text{o}}.\end{align*}$  In a sense, the calculator was 'imagining' the triangle on the right while you were imagining the triangle on the left - both are possible with the given information.
  ::您计算器上的反正正弦函数只产生 0和 90°之间的角。 从某种意义上说,计算器在您想象左侧三角时“ 想象” 右侧的三角形, 使用给定的信息, 两者都是可能的 。

  播放段落

  This is a problem when using the Law of Sines to solve for missing angles. If the information you are given fits SSA, it is possible that there are two answers. If you have a figure drawn to scale , you  may be able to determine whether your answer should be the acute angle or the obtuse angle by looking at the figure .
  ::当使用 Sines 法则解决缺失角度时,这是一个问题。 如果给您的信息符合 SSA, 则可能有两个答案。 如果您有用于缩放的数字, 您也许可以通过查看该图来确定您的答案应该是急性角度还是隐蔽角度 。

  播放段落

  Example 3
  ::例3

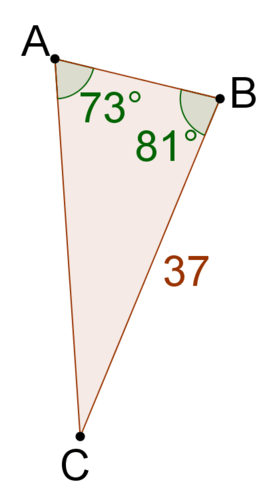
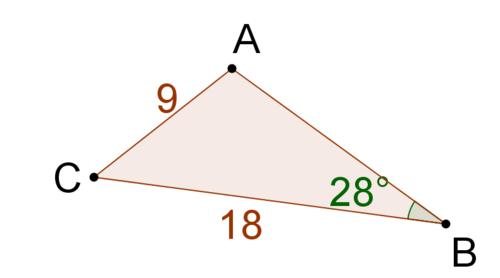
  播放段落

  The triangle below is drawn to scale. Use the Law of Sines to solve for the measure of angle $\begin{align*}C.\end{align*}$
  ::下面的三角形被拉到比例。 使用 Sines 法则来解析角度 C 的测量 。

  播放段落

  
  $\begin{align*}\angle C\end{align*}$ appears to be obtuse. Match angles with opposite sides.
  ::QC似乎有点模糊, 角度对齐, 角度对齐, 角度对齐, 角度对齐, 角度对齐, 角度对齐, 角度对齐, 角度对齐, 角度对齐, 角度对齐, 角度对齐, 角度对齐, 角度对齐, 角度对齐, 角度对齐, 角度对齐, 角度对齐, 角度对齐, 角度对齐, 角度对齐, 角度对齐, 角度对对齐, 角度对齐, 角度对齐, 角度对齐, 角度对齐, 角度对齐, 角度对齐, 角度对齐, 角度对齐, 角度对齐, 角度对齐, 角度对齐, 角度对齐, 角度对齐, 角度对齐, 角度对齐

  播放段落

  $$\begin{align*}\frac{\sin 28^{\text{o}}}{17} &= \frac{\sin C}{33}\\ \sin C &= \frac{33 \sin 28^{\text{o}}}{17}\vphantom{\sum^X_X}\\ m \angle C &= \sin^{\text{-}1} \left(\frac{33 \sin 28^{\text{o}}}{17}\right)\\ m \angle C & \approx 65.7^{\text{o}}\end{align*}$$
  ::Sin28o17=sinC33sinC=33sin28o17XXmC=sin-1(33sin28o17mC65.7o)

  播放段落

  This is the acute version of the answer. You know the angle should be obtuse, so find the angle supplementary to $\begin{align*}65.7^\circ\end{align*}$ :
  ::这是答案的急切版本。 您知道角度应该是模糊的, 所以找到对65.7的补充角度 :

  $\begin{align*}180^\circ-65.7^\circ=114.3^\circ\end{align*}$

  播放段落

  Based on the given info: $\begin{align*}m \angle C=114.3^{\text{o}}.\end{align*}$
  ::根据上述信息:mC=114.3o。

  Summary

  播放段落 Law of Sines: $\begin{align*}\frac{\sin A}{a}=\frac{\sin B}{b}=\frac{\sin C}{c}\end{align*}$   ::Sines法律:SinAa=sinBb=sinCc

  ---

  播放段落

  Review
  ::审查审查审查审查

  播放段落

  For each triangle, find the measure of all missing sides and angles.
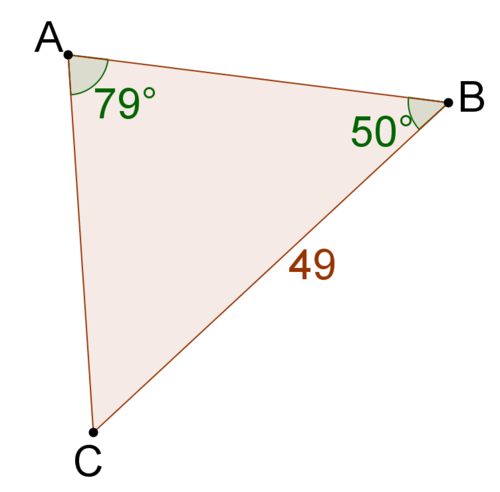
  ::每个三角形, 找到所有缺失的侧面和角度的测量值 。

  1.

  

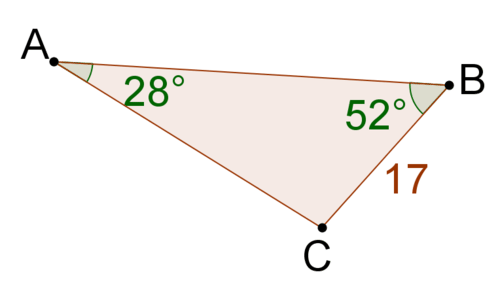
  2 .

  

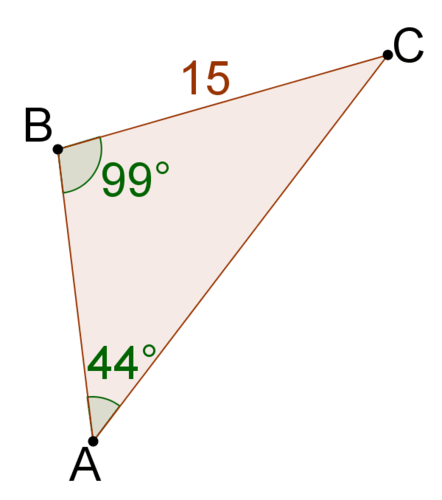
  3.

  

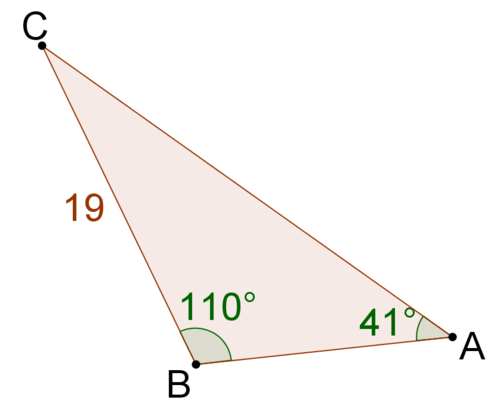
  4.

  

  5.

  

  6.

  

  7.

  

  8.

  

  播放段落

  9. What does SSA have to do with the Law of Sines? What type of problems do you have to think extra carefully about to make sure you have the correct answer?
  ::9. 特别敏感问题与辛尼定律有什么关系?你必须仔细考虑哪些类型的问题才能确保你得到正确的答案?

  播放段落

  10. The triangle below is drawn to scale. Determine the measure of each of the missing angles.
  ::10. 以下三角形被划为缩放大小,确定每个缺失角度的度量。

  

  播放段落

  11. The triangle below is drawn to scale. Determine the measure of each of the missing angles.
  ::11. 以下三角形被划为缩放大小,确定每个缺失角度的度量。

  

  播放段落

  12. The triangle below is drawn to scale. Determine the measure of each of the missing angles.
  ::12. 下面的三角形被画为缩放大小,确定每个缺失角度的度量。

  

  播放段落

  13. Use the picture below to derive the Law of Sines.
  ::13. 利用下面的图景来得出《辛那斯定律》。

  

  播放段落

  14. What type of problems can you solve with the Law of Sines?
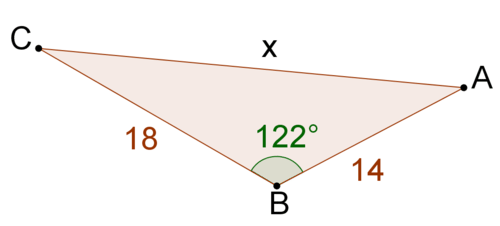
  ::十四、用辛尼定律可以解决哪类问题?

  播放段落

  15. Explain why you cannot use the Law of Sines to solve for $\begin{align*}x\end{align*}$ in the triangle below.
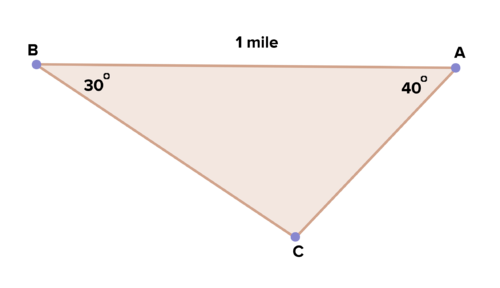
  ::15. 解释为什么你不能使用辛那斯定律来解决以下三角形中的 x 。

  

  播放段落

  16. A park ranger at a watch tower at point A spots a fire at point C. She measures the angle between the trail and the fire at 40 degrees. She hikes along a straight trail for 1 mile, observing the fire as she goes. She stops at point B and measures the angle between the fire and the trail at 30 degrees. How far is she from the fire?
  ::16. A点的守望塔的公园护林员在C点点点点点火点火点C点,她测量道与火之间的角为40度,沿直道走1英里,在她行进时观察着火点,在B点站着,将火点与路点之间的角测量在30度。她离火点有多远?

  

  播放段落

  17. A hiker is walking through a flat meadow, observing a mountain in the distance. She measures the angle of elevation between the ground and the mountaintop to be 25 degrees. She walks 5 miles, and then measures the angle of elevation again—now it's 40 degrees. How tall is the mountain?
  ::17. 远足者正在穿过平坦的草原,在远处观察一座山,她测量地表和山顶之间的高度角为25度,走5英里,然后再测量高地的角,现在是40度,山有多高?

  播放段落

  Review (Answers)
  ::审查(答复)

  播放段落

  Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
  ::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键 。