课程： 7.8 应用问题三角-interactive

章节大纲

选择节常规

折叠展开
常规

全部折叠展开全部
- 选择活动新闻通告
  
  新闻通告讨论区

应用问题三角

There are many different problems you can solve with your knowledge of triangles and trigonometry. Here is a summary of all the key facts and formulas that will be helpful.
::您对三角形和三角测量的知识可以解决许多不同的问题。这里是所有关键事实和公式的总结,这将有助于解决问题。

TRIANGLE SUMMARY :
::笔录摘要:

The sum of the measures of the three angles in a triangle is $\begin{aligned} 180^{o} . \end{aligned}$
::三角形中三个角度的测量总和是180o。

In , the sides are in the ratio $\begin{aligned} 1 : \sqrt{3} : 2 \end{aligned}$

::双方比例为1:3:2

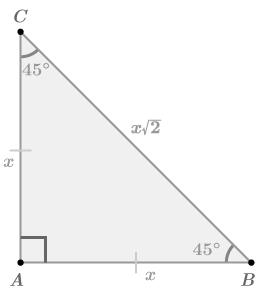
In , the sides are in the ratio $\begin{aligned} 1 : 1 : \sqrt{2} \end{aligned}$

::在1:1:2的比例中,两边的比例为1:1:2。

states that for a right triangle with legs $\begin{aligned} a \end{aligned}$ and $\begin{aligned} b \end{aligned}$ and hypotenuse $\begin{aligned} c \end{aligned}$ , $\begin{aligned} a^{2} \end{aligned}$ $\begin{aligned} + \end{aligned}$ $\begin{aligned} b^{2} \end{aligned}$ $\begin{aligned} = \end{aligned}$ $\begin{aligned} c^{2} \end{aligned}$
::a2+b2=c2)

SOH CAH TOA is a mnemonic device to help you remember the three trigonometric ratios:
::SOH CAH ToA是一个内温设备, 帮助您记住三个三角比:

$\begin{aligned} \sin θ = \end{aligned}$ $\begin{aligned} \frac{opposite leg}{hypotenuse} \end{aligned}$ $\begin{aligned} \cos θ = \end{aligned}$ $\begin{aligned} \frac{adjacent leg}{hypotenuse} \end{aligned}$ $\begin{aligned} \tan θ = \end{aligned}$ $\begin{aligned} \frac{opposite leg}{adjacent leg} \end{aligned}$
::

The : $\begin{aligned} \frac{\sin A}{a} = \frac{\sin B}{b} = \frac{\sin C}{c} \end{aligned}$ (watch out for the SSA case)
::SinAa=sinBb=sinCc(注意SSA案件)

The : $\begin{aligned} c^{2} = a^{2} + b^{2} - 2 a b \cos C \end{aligned}$
::C2=a2+b2-2abcos=C :c2=a2+b2-2abcos=2abcos=C

The area of a triangle is $\begin{aligned} \frac{1}{2} b h \end{aligned}$ or $\begin{aligned} \frac{1}{2} a b \sin C \end{aligned}$
::三角形区域为 12bh 或 12absinC

Real-World Application: Boating
::现实世界应用:船运

If a boat travels 4 miles SW (southwest) and then 3 miles NNW (north-northwest), how far away is the boat from its starting point?
::如果一艘船在西南4英里处行驶,然后在西北3英里处行驶,船离起点有多远?

First, think about what southwest and north-northwest mean. The picture below shows the four basic directions of north, south, east, and west. It also shows southwest and northwest. North-northwest is directly in between northwest and north. Make sure you understand where the angles in the picture came from.
::首先,想想西南和西北意味着什么。下图显示了北、南、东和西的四条基本方向。它也显示了西南和西北。西北直接位于西北和北之间。请确保您了解图片的角来自何方。

Next, draw a picture of the movements of the boat, in order . 4 miles SW, followed by 3 miles NNW:
::接下来,绘制一幅船动向图,按顺序排列。西南4英里,然后是西北3英里:

Note that the angle between the SW direction and the NNW direction is $\begin{aligned} {22.5}^{o} + 45^{o} = {67.5}^{o} \end{aligned}$ .
::请注意,南纬方向与西北地区方向之间的角为22.5o+45o=67.5o。

Now make a plan for how you will solve. Look to see what is given and what you are looking for and think about what method or technique would be helpful. In this situation, you have two sides and an included angle and are looking for the third side . You can use the Law of Cosines.
::制定解决计划。看看给什么,你要找什么,想想方法或技巧会有什么帮助。在这种情况下,你有两个侧面,一个包含角度,并正在寻找第三侧。你可以使用“科辛定律 ” 。

Now that you have a plan, you can solve the problem. In the formula f or the Law of Cosines, 3 and 4 are the values for $\begin{aligned} a \end{aligned}$ and $\begin{aligned} b \end{aligned}$ and $\begin{aligned} {67.5}^{o} \end{aligned}$ is the value for $\begin{aligned} ∠ C \end{aligned}$ . Side $\begin{aligned} x \end{aligned}$ is across from the known angle, so it is $\begin{aligned} c . \end{aligned}$
::现在有了计划,你可以解决问题。在科辛定律公式中,3和4是a和b的值,67.5ois的值是+C的值。Sidex是已知角度的对面,所以是c。

$\begin{aligned} a^{2} + b^{2} - 2 a b \cos C & = c^{2} \\ 3^{2} + 4^{2} - 2 (3) (4) (\cos 67.5) & = x^{2} \\ 9 + 16 - 9.18 & = x^{2} \\ 15.82 & = x^{2} \\ x & \approx 3.98 \end{aligned}$
::a2+b2-2abcosC=c232+42-2(3)(cos67.5)=x29+16-9.18=x215.82=x2x%3.98

The boat is 3.98 miles from its starting place.
::船离起点3.98英里

Real-World Application: Observation Points
::现实世界应用:观察点

1. From the fourth story of a building (65 feet) Mark observes a car driving towards the building on the street below. If the angle of depression of the car changes from $\begin{aligned} 15^{o} \end{aligned}$ to $\begin{aligned} 45^{o} \end{aligned}$ while he watches, how far did the car travel?
::1. Mark从关于一栋建筑(65英尺)的第四个故事中看到一辆汽车在下面街道上驶向大楼,如果汽车的压抑角度从15度到45度时从15度到45度变化,车走多远?

Start by making a detailed picture of the situation and labeling what you know.
::首先详细描述情况标出你所知道的

Note that $\begin{aligned} 15^{o} + 30^{o} = 45^{o}, \end{aligned}$ so $\begin{aligned} 45^{o} \end{aligned}$ is the angle of depression for the ending location of the car.
::请注意,15o+30o=45o,so 45o是汽车末端位置的压抑角度。

Now make a plan for how you will solve. Consider what is given and what you are looking for and think about what method or technique would be helpful.
::现在为你们将如何解决制定一个计划。想想给什么和你们正在寻找什么,想想什么样的方法或技巧会有所帮助。

In this situation, you have two right triangles (the smaller triangle and the larger triangle). In each case, you know a side and an angle. You are looking for a portion of one of the sides of these triangles $\begin{aligned} (x) \end{aligned}$ .
::在此情况下, 您有两个右三角形( 小三角形和大三角形) 。在每种情况下, 您知道一个侧面和一个角度。您正在寻找这些三角形( x) 的侧面的一部分。

You can use trigonometric ratios to find the missing sides of these triangles to help you to find the length of $\begin{aligned} x \end{aligned}$ .
::您可以使用三角比来找到这些三角形的缺失侧, 来帮助您找到 x 的长度。

First look at the small triangle . Side $\begin{aligned} y \end{aligned}$ is opposite the $\begin{aligned} 45^{o} \end{aligned}$ angle and 65 is adjacent to the $\begin{aligned} 45^{o} \end{aligned}$ angle. This is a tangent relationship (or you could use 45-45-90 triangle ratios):
::首先看小三角形。侧面 y 在 45 方形对面, 65 在 45 方形附近。这是一个正切关系( 或者您可以使用 45- 45- 90 三角形比 ) :

$\begin{aligned} \tan 45^{o} & = \frac{y}{65} \\ y & = 65 \tan 45^{o} \\ y & = 65 ft \end{aligned}$
::Tan45o=y65y=65tan45oy=65英尺

Now look at the larger right triangle . Side $\begin{aligned} x + y \end{aligned}$ is opposite the $\begin{aligned} 75^{o} \end{aligned}$ angle $\begin{aligned} (30^{o} + 45^{o} = 75^{o}) \end{aligned}$ and 65 is adjacent to the $\begin{aligned} 75^{o} \end{aligned}$ angle. Again you can use tangent.
::现在看看较大的右三角形。侧面 x+y 与 75o 角度( 30o+45o=75o) 相对, 65 与 75oangle 相邻。您可以再次使用正切值。

$\begin{aligned} \tan 75^{o} & = \frac{x + y}{65} \\ 65 \tan 75^{o} & = x + y \\ x + y & \approx 242.58 ft \end{aligned}$
::tan@ 75o=x+y6565tan75o=x+yx+yx+y242. 58英尺

Since $\begin{aligned} y = 65 ft, \end{aligned}$ $\begin{aligned} x \end{aligned}$ must equal $\begin{aligned} 242.58 - 65 = 177.58 ft . \end{aligned}$
::由于y=65英尺,x必须等于242.58-65=177.58英尺。

The car traveled 177.58 feet.
::汽车行驶了177.58英尺。

2. Karen is 5.5 feet tall and looks up at a $\begin{aligned} 40^{o} \end{aligned}$ angle to see the top of the flagpole in front of a building. She is standing 40 feet from the flagpole. How tall is the flagpole?
::2. Karen身高5.5英尺,望着一个40角角的柱子,望着一栋大楼前面的旗杆顶部,站在离旗杆40英尺处,旗杆有多高?

Again, start by making a detailed picture of the situation and labeling what you know.
::再说一遍,首先详细描述情况,标出你所知道的。

Now, make a plan for how you will solve. Look to see what is given and what you are looking for and think about what method or technique would be helpful. In this situation, you have a right triangle . You know an angle ( $\begin{aligned} 40^{o} \end{aligned}$ ), and a side ( $\begin{aligned} 40 ft \end{aligned}$ ) within the right triangle. You are looking for another side of the triangle $\begin{aligned} (x) \end{aligned}$ .
::现在,请为您如何解答制定计划。看看给什么,你正在寻找什么, 想想什么样的方法或技巧会有帮助。在这种情况下, 您有一个正确的三角形。您知道右三角形的角( 40o) , 右三角形的侧面( 40 ft) 。您正在寻找三角形的另一边( x) 。

Think of the flagpole as being made up of two pieces . The first piece is Karen's height of 5.5 feet. The next piece is the rest of the flagpole that is taller than Karen ( $\begin{aligned} x \end{aligned}$ in the picture above). Side $\begin{aligned} x \end{aligned}$ is opposite the $\begin{aligned} 40^{o} \end{aligned}$ angle and 40 ft is adjacent to the $\begin{aligned} 40^{o} \end{aligned}$ angle. This is a tangent relationship.
::将旗杆想象成由两块组成。第一块是凯伦的高度为5.5英尺。下一块是比凯伦( 以上图片中的x) 高的旗杆的其余部分。侧面 x 与 40 角对面, 40 英尺与 40 角相邻。这是一个正切的关系。

$\begin{aligned} \tan 40^{o} & = \frac{x}{40} \\ x & = 40 \tan 40^{o} \\ x & \approx 33.56 ft \end{aligned}$
::{\fn方正黑体简体\fs18\b1\bord1\shad1\3cH2F2F2F}泰诺40o=x40x=40tan_40ox}33.56英尺

Therefore, the complete height of the flagpole is approximately $\begin{aligned} 33.56 + 5.5 = 39.06 feet . \end{aligned}$
::因此,旗杆的完整高度约为33.56+5.5=39.06英尺。

Examples
::实例实例实例实例

Example 1
::例1

A community garden is being built in your neighborhood. The garden will be triangular in shape and a fence will surround the garden. Two sides of the garden will be 33 feet and 24 feet. The angle between those two sides will measure $\begin{aligned} 62^{o} . \end{aligned}$ Find the area and perimeter of the garden.
::在你的邻里正在建造一个社区花园,花园的形状将是三角形的,花园周围将有一个栅栏,花园的两侧将为33英尺和24英尺,两侧之间的角将测量62o。找到花园的面积和周围。

Start by drawing a picture and carefully labeling everything that you know.
::首先绘制一张图片仔细标注你知道的一切

To find the area of the garden you can use the sine area formula.
::要找到花园的面积,您可以使用正弦区域公式。

$\begin{aligned} A & = \frac{1}{2} (33) (24) \sin 62^{o} \\ A & \approx 349.6 {ft}^{2} \end{aligned}$
::A=12(33) (24)sin 62oA 349.6平方英尺

In order to find the perimeter of the garden you need to know the length of the third side. In this situation you know two sides and an included angle , so you can use the Law of Cosines to find the length of the third side .
::为了找到花园的周边, 您需要知道花园的第三侧的长度。在此情况下, 您知道两侧和一个包含的角度, 这样您就可以使用科辛斯定律来找到第三侧的长度。

$\begin{aligned} 33^{2} + 24^{2} - 2 (33) (24) \cos 62^{o} & = x^{2} \\ 1089 + 576 - 743.64 & = x^{2} \\ 921.36 & = x^{2} \\ x & \approx 30.35 ft \end{aligned}$
::332+242-2.33(24cos62o=x21089+576-743.64=x2921.36=x2x30.35英尺)

Now that you know the length of the third side, you can find the perimeter of the garden.
::现在你知道第三边的长度了你可以找到花园的周边

$\begin{aligned} P = 33 + 24 + 30.35 = 87.35 ft \end{aligned}$
::P=33+24+30.35=87.35英尺

Example 2
::例2

A surveyor wants to find the distance from points $\begin{aligned} A \end{aligned}$ and $\begin{aligned} B \end{aligned}$ to an inaccessible point $\begin{aligned} C \end{aligned}$ . These three points form a triangle. Standing at point $\begin{aligned} A \end{aligned}$ , he finds $\begin{aligned} m ∠ A \end{aligned}$ in the triangle is equal to $\begin{aligned} 60^{\circ} \end{aligned}$ . Standing at point $\begin{aligned} B \end{aligned}$ , he finds $\begin{aligned} m ∠ B \end{aligned}$ in the triangle is equal to $\begin{aligned} 55^{o} \end{aligned}$ . He measures the distance from point $\begin{aligned} A \end{aligned}$ to point $\begin{aligned} B \end{aligned}$ and finds it to be 350 feet. Find the distance from points $\begin{aligned} A \end{aligned}$ and $\begin{aligned} B \end{aligned}$ to point $\begin{aligned} C \end{aligned}$ .
::测量员希望找到从A点和B点到无法进入的C点之间的距离。这三个点形成三角。站在A点, 他发现三角的 mA 等于 60 。站在B点, 他发现三角的 mB 等于 55o 。他测量了从A点到B点的距离, 发现距离是 350 英尺。找到从 A点和B点到C点的距离。

Draw a picture of this situation.
::绘制此情形的图片。

Example 3
::例3

Make a plan: what method(s) or technique(s) can you use to solve this problem?
::制定计划:您可以使用何种方法或技术来解决这个问题?

You can find the measure of angle $\begin{aligned} C \end{aligned}$ using the fact that the sum of the measures of the three angles in a triangle is $\begin{aligned} 180^{o} . \end{aligned}$ Then, you will know all the angles and one side. You could then use the Law of Sines to set up equations to find $\begin{aligned} A C \end{aligned}$ and $\begin{aligned} B C \end{aligned}$ .
::您可以使用三角形中三个角度的测量总和为 180o 来找到角度C 。然后, 您就会知道所有角度和一面。然后, 您可以使用 Sines 定律来设置方程式以查找 AC 和 BC 。

Example 4
::例4

Solve the problem.
::解决问题

$\begin{aligned} m ∠ C = 65^{o} . \end{aligned}$ Now use the Law of Sines twice:
::MC=65o 现在使用Sines定律两次:

To find $\begin{aligned} A C \end{aligned}$ :
::要找到 AC :

To find $\begin{aligned} B C \end{aligned}$ :
::要找到 BC :

The distance from $\begin{aligned} A \end{aligned}$ to $\begin{aligned} C \end{aligned}$ is approximately 316 feet and the distance from $\begin{aligned} B \end{aligned}$ to $\begin{aligned} C \end{aligned}$ is approximately 334 feet.
::从A到C的距离约为316英尺,从B到C的距离约为334英尺。

Remember this!

The Triangle Sum Theorem says that the three interior angles of any triangle add up to 180 ^o .
::三角形苏莫雷姆说任何三角形的三个内角加起来等于180o

In 30-60-90 right triangles , the sides are in the ratio $\begin{aligned} 1 : \sqrt{3} : 2. \end{aligned}$
::在30-60-90个右三角中,两边的比例为1:3:2。

In 45-45-90 right triangles , the sides are in the ratio $\begin{aligned} 1 : 1 : \sqrt{2} . \end{aligned}$
::在45 - 45 - 90 右三角中,两边的比例为1: 1 2。

The Pythagorean Theorem shows a relationship between the three sides of a right triangle: $\begin{aligned} a^{2} + b^{2} = c^{2} \end{aligned}$
::Pythatagorean 理论显示右三角形的三边之间的关系: a2+b2=c2

The three trig ratios are: $\begin{aligned} \sin (θ) = \frac{opp}{hyp} \end{aligned}$ , $\begin{aligned} \cos (θ) = \frac{adj}{hyp} \end{aligned}$ , $\begin{aligned} \tan (θ) = \frac{opp}{adj} \end{aligned}$
::三种三重比率是:sin()=opphyp,cos()=adjhyp,tan()=oppadj。

Law of Sines: $\begin{aligned} \frac{\sin A}{a} = \frac{\sin B}{b} = \frac{\sin C}{c} \end{aligned}$
::Sines定律:sinAa=sinBb=sinCc

Law of Cosines: $\begin{aligned} a^{2} + b^{2} - 2 a b \cos C = c^{2} \end{aligned}$
::科士定律:a2+b2-2abcos=C=c2

Area of a triangle $\begin{aligned} A = \frac{1}{2} (a) (b) \sin C \end{aligned}$
::A=12(a)(b)sinC三角形区域

Review
::审查审查审查审查

The angle of depression of a boat in the distance from the top of a lighthouse is $\begin{aligned} 25^{o} . \end{aligned}$ The lighthouse is 200 feet tall. Find the distance from the base of the lighthouse to the boat.
::离灯塔顶部距离的船只的压抑角度是25o,灯塔200英尺高,找到灯塔底部至船的距离。

1. Draw a picture of this situation.
::1. 描绘一下这种情况。

2. Make a plan: what method(s) or technique(s) can you use to solve this problem?
::2. 制定计划:您可使用何种方法或技术来解决这一问题?

3. Solve the problem.
::3. 解决问题。

A pilot is flying due west and gets word that a major storm is in her path. She turns the plane $\begin{aligned} 40^{o} \end{aligned}$ to the left of her intended course and continues the flying. After passing the storm, she turns $\begin{aligned} 50^{o} \end{aligned}$ to the right, and flies until she has returned to her original flight path. At this point she is 75 miles from where she left her original path when she first made a turn. How much further did the pilot fly as a result of the detour?
::一位飞行员正向西飞行,并得知她正走在路上,她将40o号飞机转向她预定航道的左边,继续飞行。经过风暴后,她向右转50o,飞到她回到原来的飞行路线。此时,她离她刚转弯时离开原路的75英里。驾驶员绕道飞了多远?

4. Draw a picture of this situation.
::4. 描绘一下这种情况。

5. Make a plan: what method(s) or technique(s) can you use to solve this problem?
::5. 制定计划:您可使用何种方法或技术来解决这一问题?

6. Solve the problem.
::6. 解决问题。

A new bridge is being built across a river in your town. You want to figure out how long the bridge will be. You find two points on one side of the river that are 30 feet apart. These two points with the point at the end of the bridge on the other side of the river form a triangle. You stand at each of the two points on your side of the river and measure the angles of the triangle. You find the two angles are $\begin{aligned} 45^{o} \end{aligned}$ and $\begin{aligned} 70^{o} . \end{aligned}$ How far are each of the two points on your side of the river from the end of the bridge on the other side of the river? How long will the bridge be?
::正在你镇上的一条河上建造一座新桥。您想要弄清楚桥的长度。您在河的一边发现两点, 距离为30英尺。这两个点与河的另一边的桥端的两点形成三角形。您站在河的另一边的两点中, 并测量三角形的角。您发现两个角度是 45oand 70o 。您在河的另一边的两点中, 距离河的另一边的桥端各多远? 桥还要站多久?

7. Draw a picture of this situation.
::7. 描述一下这种情况。

8. Make a plan: what method(s) or technique(s) can you use to solve this problem?
::8. 制定计划:你可以使用何种方法或技术来解决这个问题?

9. Solve the problem.
::9. 解决问题。

$\begin{aligned} △ A B C \end{aligned}$ has two sides of length 12 and a non-included angle that measures $\begin{aligned} 60^{o} . \end{aligned}$
::ABC有长度12的两面和一个不包含的角度,以60度计。

10. Draw a possible picture of this situation.
::10. 说明这种情况的可能情况。

11. Find the measure of all sides and angles of $\begin{aligned} △ A B C . \end{aligned}$
::11. 找出ABC的方形和角度。

12. Find the area of $\begin{aligned} △ A B C . \end{aligned}$
::12. 寻找 ABC 区域。

Lily starts at point A and walks straight for 100 feet. Then, she turns right at an $\begin{aligned} 80^{o} \end{aligned}$ angle and continues walking for another 150 feet. In order to go straight back to her starting place, how far will she need to walk? At want angle should she turn right?
::Lily从A点开始,直走100英尺。然后,她右转80角,继续走150英尺。为了直接回到起点,她需要走多远?她应该右转多少角度?

13. Draw a picture of this situation.
::13. 描述一下这种情况。

14. Make a plan: what method(s) or technique(s) can you use to solve this problem?
::14. 制定计划:您可使用何种方法或技术来解决这一问题?

15. Solve the problem.
::15. 解决问题。

16. Create a triangle such that the two sides and a non-included angle are known. Find the possible measures of the included angle. How many solutions resulted? Explain why. Recreate the triangle from scratch so that there are a number of different solutions. Explain the results.
::16. 创建一个三角形,使两边和未包含角度都为人所知。找到包含角度的可能度量。结果有多少个解决方案?解释原因。从零开始重新创建三角形,这样就有一些不同的解决方案。解释结果。

17. Create a scenario which can be solved with the law of sines. Create another scenario that can be solved with the law of cosines. Solve both.
::17. 创造一种可以用正弦法解决的情景; 创造另一种可以用共弦法解决的情景; 解决这两种问题。

Review (Answers)
::审查(答复)

Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键。

章节大纲

常规

应用问题三角

Real-World Application: Boating ::现实世界应用:船运

Real-World Application: Observation Points ::现实世界应用:观察点

Examples ::实例实例实例实例

Example 1 ::例1

Example 2 ::例2

Example 3 ::例3

Example 4 ::例4

Review ::审查审查审查审查

Review (Answers) ::审查(答复)