8.2 圆圆圆圈和圆圈区域的环形-公式、互动和实例-interactive

章节大纲

• 选择节常规

  折叠 展开

  常规

  全部折叠 展开全部

  • 选择活动新闻通告

    

    新闻通告 讨论区
• 选择节圆圆圆圈和圆圆圈区域的环形----公式、互动和实例

  折叠 展开

  圆圆圆圈和圆圆圈区域的环形----公式、互动和实例

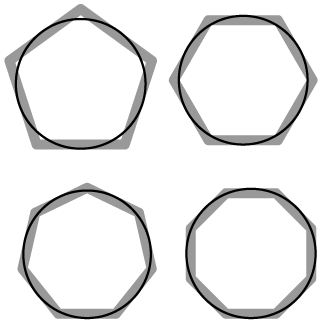
  A circle is a simple closed curve, with a set of all points at a constant distance from a fixed (center) point $\begin{array}{r}A\end{array}$ , in the same plane . Since the circle has only one center , you can name the circle by naming its center. As such, you can name this as circle $\begin{array}{r}A\end{array}$ .

  The radius of a circle $\begin{array}{r}r\end{array}$ , is the distance from the center of the circle to the circle. All circles are geometrically similar .

  Archimedes , a mathematician in ancient Greece, is credited for figuring out the method for approximating the value of pi . He drew a regular polygon inscribed within the circle to approximate $\begin{array}{r}\pi \end{array}$ , and the more sides he drew on the polygon , the better approximation to $\begin{array}{r}\pi \end{array}$ he would get.

  It had long been recognized that the ratio of the circumference ( perimeter of a circle) of a circle to its diameter was $\begin{array}{r}\pi \end{array}$ . The number $\begin{array}{r}\pi \end{array}$ is a mathematical constant. For every circle, the ratio between the and diameter of any circle is approximately equal to 3.14159. The interactive below provides a walkthrough on the value of pi.

  播放段落

  Approximating Pi with Inscribed Polygons
  ::与被附多边形相近的 Pi 相近的 Pi

  播放段落

  Drag the orange dot to increase or decrease the number of sides of the polygon. Observe that as the number of sides increases, the area of the polygon approximates the area of a circle and we get a better approximation to $\begin{array}{r}\pi .\end{array}$
  ::拖曳橙色点以增加或减少多边形的边数。 注意随着边数的增加, 多边的面积接近圆的面积, 我们的近似值会更好 。

  播放段落

  Area and Circumference of a Circle
  ::圆圈的面积和环环

  Because $\begin{array}{r}\pi \end{array}$ is the ratio between the circumference and the diameter, the circumference of a circle is equal to the diameter times $\begin{array}{r}\pi \end{array}$ .

  $\begin{array}{r}C=\pi d\end{array}$

  Area of a circle is the region occupied by the circle in a two-dimensional plane. The formula for the area of a circle can be derived by dissecting a circle into wedges and rearranging them to form a shape that is close to a . The parallelogram can then be formed into a shape close to a rectangle .

  The lengths of the sides of the "parallelogram" are $\begin{array}{r}r\end{array}$ and $\begin{array}{r}\frac{2\pi r}{2}=\pi r\end{array}$ . If you imagine cutting the wedges smaller and smaller, the parallelogram will look closer and closer to a rectangle with dimensions $\begin{array}{r}\pi r\end{array}$ and $\begin{array}{r}r\end{array}$ . The area of the rectangle and thus the area of the circle will be $\begin{array}{r}(\pi r)(r)=\pi r^2\end{array}$ .

  播放段落

  Area and Circumference
  ::地区和环境

  播放段落

  Click the small blue arrow next to the image below and play with the circle by dragging the orange dot that defines the radius of the circle. The area or circumference is recalculated as you drag.
  ::单击下方图像旁边的小蓝箭头,与圆一起玩,拖曳橙色点,以决定圆半径。拖动时将重新计算区域或环形。

  播放段落

  A regular polygon is a closed figure that is both equilateral and equiangular. As the number of sides of a regular polygon increases, the polygon looks more and more like a circle.
  ::一个正则多边形是一个封闭的数字,它既是对等的,又是对等的。随着一个正则多边形的边数的增加,多边形看起来越来越像一个圆形。

  

  播放段落

  Previously you have learned that the area of a circle with radius $\begin{array}{r}r\end{array}$ is given by $\begin{array}{r}\pi r^2\end{array}$ and the circumference of a circle with radius $\begin{array}{r}r\end{array}$ is given by $\begin{array}{r}2\pi r\end{array}$ . In the examples and guided practice, you will derive these formulas by looking at the area and perimeter of regular polygons.
  ::先前您已经知道 r2 给定了半径为 r 的圆圈区域,而 r 半径为 r 的圆圈区域则给定了 。 在示例和引导练习中, 您将通过查看常规多边形的面积和周边来得出这些公式 。

  ---

  播放段落

  Finding the Area
  ::寻找“区域”

  播放段落

  1. Find the area of a regular octagon inscribed in a circle with radius 1 unit.
  ::1. 查找以圆形刻入的一正八边形区域,半径为1单位。

  播放段落

  Break the octagon into 8 congruent triangles . You will find the area of one triangle and multiply that by 8 to find the area of the whole octagon. Remember that $\begin{array}{r}360\end{array}$ is the number of degrees in a full circle. The angle formed by the equal sides of every triangle is $\begin{array}{r}\frac{{360}^{\circ }}{8}={45}^{\circ }\end{array}$ . Draw in the height for one of the triangles. The angle formed by the height and the radius of the circle is $\begin{array}{r}\frac{{45}^{\circ }}{2}={22.5}^{\circ }\end{array}$ .
  ::将八边形折成 8 个相似的三角形。 您将会发现一个三角形的面积, 并乘以 8 以找到整个八边形的面积。 记住, 360 是整个圆圈的度数。 每个三角形的等边所形成的角是 360 8= 45 . 绘制三角形之一的高度。 圆圈的高度和半径所形成的角是 45 2= 22. 。

  播放段落

  Now, you can use trigonometry to find the height and base of the triangle.
  ::现在,你可以使用三角测量来找到三角形的高度和底部。

  播放段落
  • $\begin{array}{r}\sin 22.5=\frac{0.5b}{1}\to b=2\sin 22.5\to b\approx 0.7654\end{array}$
    ::22.5=0.5b1b=2sin22.5b=0.7654
  播放段落
  • $\begin{array}{r}\cos 22.5=\frac{h}{1}\to h=\cos 22.5\to h\approx 0.9239\end{array}$
    ::-22.5=h1=h1=cos22.5\h0.9239

  播放段落

  The area of the triangle is:
  ::三角形区域为:

  播放段落

  $\begin{array}{r}A=\frac{bh}{2}=\frac{(0.7654)(0.9239)}{2}\approx 0.3536{\text{un}}^2\end{array}$
  ::A=bh2=( 0. 7654)( 0. 92392)20. 3536 un2

  播放段落

  Therefore, the area of the octagon is:
  ::因此,八边形的面积如下:

  播放段落

  $\begin{array}{r}A=8(0.3536)\approx 2.8288{\text{un}}^2\end{array}$
  ::A=8(0.3536)2.8288un2

  播放段落

  2. Find the area of a regular 60-gon inscribed in a circle with radius 1 unit and the area of a regular 120-gon inscribed in a circle with radius 1 unit.
  ::2. 找出在圆形中刻有半径1单位的正60度区域,在圆形中刻有正120度区域,在圆形中刻有半径1单位的正120度区域。

  播放段落

  While you can't accurately draw a regular 60-gon or a regular 180-gon, you can use the method from #1 to find the area of each.
  ::虽然无法准确绘制普通的 60 g 或普通的 180 g , 但您可以从 # 1 找到每个区域 。

  播放段落

  Regular 60-gon: Divide the polygon into 60 congruent triangles. Consider one of those triangles (not drawn to scale) and draw in its height. You will focus on finding the area of this triangle. The angle formed by the height and the radius of the circle is $\begin{array}{r}\frac{{360}^{\circ }}{120}=3^{\circ }\end{array}$ .
  ::常规 60 边 : 将多边形除以60 个相容的三角形。 考虑其中的一个三角形( 不是缩放的三角形) , 并在其高度中绘制。 您将集中寻找此三角形的区域 。 圆形高度和半径所构成的角是 360 120=3 。

  播放段落

  Use trigonometry to find the height and base of the triangle.
  ::使用三角测量来找到三角形的高度和底部 。

  播放段落
  • $\begin{array}{r}\sin 3=\frac{0.5b}{1}\to b=2\sin 3\to b\approx 0.1047\end{array}$
    ::3=0.5b1b=2sin 3b=0.1047
  播放段落
  • $\begin{array}{r}\cos 3=\frac{h}{1}\to h=\cos 3\to h\approx 0.9986\end{array}$
    ::CO=3=h1=h1=cos=3\h=0.9986

  播放段落

  The area of the triangle is:
  ::三角形区域为:

  播放段落

  $\begin{array}{r}A=\frac{bh}{2}=\frac{(0.1047)(0.9986)}{2}\approx 0.0523{\text{un}}^2\end{array}$
  ::A=bh2=(0.1047)(0.99862=0.0523un2)

  播放段落

  Therefore, the area of the 60-gon is:
  ::因此,60角的面积是:

  播放段落

  $\begin{array}{r}A=60(0.0523)\approx 3.138{\text{un}}^2\end{array}$
  ::A=60( 0.0523) 3.1.38 un2

  播放段落

  Regular 180-gon: Divide the polygon into 180 congruent triangles. Consider one of those triangles (not drawn to scale) and draw in its height. You will focus on finding the area of this triangle. The angle formed by the height and the radius of the circle is $\begin{array}{r}\frac{{360}^{\circ }}{360}=1^{\circ }\end{array}$ .
  ::常规 180 边形 180 边形 : 将多边形分为 180 个相似的三角形 。 考虑其中的一个三角形( 不是缩放的三角形) , 并按其高度绘制 。 您将集中寻找此三角形的区域 。 圆形高度和半径所构成的角是 360 360 =1 。

  播放段落

  Use trigonometry to find the height and base of the triangle.
  ::使用三角测量来找到三角形的高度和底部 。

  播放段落
  • $\begin{array}{r}\sin 1=\frac{0.5b}{1}\to b=2\sin 1\to b\approx 0.0349048\end{array}$
    ::=0.5b1b=2sin =1.b 0.0349048
  播放段落
  • $\begin{array}{r}\cos 1=\frac{h}{1}\to h=\cos 1\to h\approx 0.9998477\end{array}$
    ::1=h1=h1=cos1=h1=h1=h1=cos1=h1=0.9998477

  播放段落

  The area of the triangle is:
  ::三角形区域为:

  播放段落

  $\begin{array}{r}A=\frac{bh}{2}=\frac{(0.0349048)(0.9998477)}{2}\approx 0.0174482{\text{un}}^2\end{array}$
  ::A=bh2=( 0.0 349048) (0. 99984772) 0.0174482un2

  播放段落

  Therefore, the area of the 180-gon is:
  ::因此,180方形的面积是:

  播放段落

  $\begin{array}{r}A=180(0.0174482)\approx 3.141{\text{un}}^2\end{array}$
  ::A=180( 0.01744482) 3.1.41 un2

  播放段落

  Now, let's explore how area can change based on the number of sides.
  ::现在,让我们来探索一下,根据方位数,区域如何变化。

  播放段落

  What happens to the area of the regular polygon as the number of sides increases? Make a conjecture about the area of a circle with radius 1 unit.
  ::随着边数的增加,正多边形区域会怎样?对圆圈区域以半径 1 单位进行推测。

  播放段落

  You have the following information:
  ::您拥有以下信息:

  播放段落 Number of Sides ::侧数数	8	60	180
  播放段落 Area ::地区面积	2.8288	3.138	3.141

  播放段落

  As the number of sides increases, the regular polygon will get closer and closer to the circle that inscribes it. Therefore, the area of the regular polygon will get closer and closer to the area of the circle. Notice that as the number of sides went from 60 to 180, the area barely changed, staying around 3.14. If you increase the number of sides to 1000, you will find that the area of the regular polygon is still approximately 3.14157. You should recognize these numbers as approximately the value of $\begin{array}{r}\pi \end{array}$ .
  ::随着边数的增加,正多边形的正多边形将越来越接近其注册的圆圈。因此,正多边形的面积将越来越接近圆圈的区域。请注意,随着边数从60到180,区域几乎没有变化,停留在3.14左右。如果将边数增加到1000,你就会发现正多边形的面积仍然约为3.14157。你应该认识到这些数字大约是__。

  播放段落

  As the number of sides increases, the polygon becomes closer and closer to a circle, and the area gets closer and closer to $\begin{array}{r}\pi {\text{un}}^2\end{array}$ . A conjecture would be that the area of a circle with radius 1 unit is $\begin{array}{r}\pi {\text{un}}^2\end{array}$ .
  ::随着边数的增加,多边形越来越接近圆形,区域也越来越接近 un2。 一种推测是,圆圆的半径为1单位的面积是 un2。

  ---

  播放段落

  Examples
  ::实例实例实例实例

  播放段落

  Example 1
  ::例1

  播放段落

  You can use regular polygons with an increasing number of sides to help explain why a circle of radius 1 unit has an area of $\begin{array}{r}\pi {\text{un}}^2\end{array}$ . Where does the $\begin{array}{r}{r}^2\end{array}$ come from in the formula for the area of a circle?
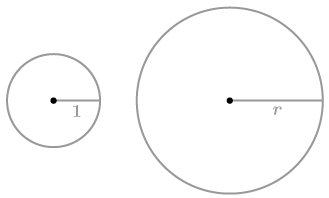
  ::您可以使用正则多边形, 边边数越来越多, 帮助解释为什么半径 1 单位的圆圈面积为 un2 。 r2 是从圆区域公式中哪来的?

  播放段落

  Remember that all circles are similar. To create another circle with radius $\begin{array}{r}r\end{array}$ from a circle with radius 1 unit, apply a similarity transformation with scale factor $\begin{array}{r}k=\text{radius}\end{array}$ .
  ::记住所有圆圈都是相似的。 要从一个半径 1 单位的圆上创建另一个半径为 r 的圆圈, 请应用比例系数 k= radios 的相似性转换 。

  

  播放段落

  The area of the transformed circle is $\begin{array}{r}{k}^2\end{array}$ times the area of the original circle. Because the area of the original circle is $\begin{array}{r}\pi \end{array}$ and the scale factor is equal to $\begin{array}{r}r\end{array}$ , the area of the transformed circle is $\begin{array}{r}\pi r^2\end{array}$ . This is one way to explain why the formula for the area of a circle is $\begin{array}{r}\pi r^2\end{array}$ .
  ::变形圆的面积是原圆面积的 k2 次。 因为原圆的面积是 __ , 比例系数等于 r, 变形圆的面积是 r2 。 这是解释圆面积公式为何为 r2 的一种方式。

  播放段落

  Example 2
  ::例2

  播放段落

  Find the perimeter of a regular octagon inscribed in a circle with radius 1 unit.
  ::查找以圆形刻入一半径1单位的正八边形周界。

  播放段落

  The base of one triangle was $\begin{array}{r}b=2\sin 22.5\to b\approx 0.7654\end{array}$ . Therefore, the perimeter of the octagon is $\begin{array}{r}P\approx 8(0.7654)=6.1232\text{un}\end{array}$ .
  ::一个三角的底部是b=2sin22.5b0.7654。因此,八边形的周边是P8(0.7654)=6.1232un。

  播放段落

  Example 3
  ::例3

  播放段落

  Find the perimeter of a regular 60-gon inscribed in a circle with radius 1 unit.
  ::查找以圆形标注的正常的60度的周界,以圆形标注,半径为1单位。

  播放段落

  The base of one triangle was $\begin{array}{r}b=2\sin 3\to b\approx 0.1047\end{array}$ . Therefore, the perimeter of the 60-gon is $\begin{array}{r}P\approx 60(0.1047)=6.282\text{un}\end{array}$ .
  ::一个三角的底部是b=2sin3b0.1047。因此,60角的周边是P60(0.1047)=6.282un。

  播放段落

  Example 4
  ::例4

  播放段落

  Find the perimeter of a regular 180-gon inscribed in a circle with radius 1 unit.
  ::查找以圆形标注的180度正方形的圆周界,半径为1单位。

  播放段落

  The base of one triangle was $\begin{array}{r}b=2\sin 1\to b\approx 0.0349048\end{array}$ . Therefore, the perimeter of the 180-gon is $\begin{array}{r}P\approx 180(0.0349048)=6.283\text{un}\end{array}$ .
  ::一个三角的底部是b=2sin1b0.0349048。因此,180角的周边是P180(0.0349048)=62.83un。

  播放段落

  Example 5
  ::例5

  播放段落

  Make a conjecture about the circumference of a circle with radius 1 unit.
  ::猜测圆环的环形,半径1单位。

  播放段落

  The perimeters from Example #2, Example #3, and Example #4 are approaching $\begin{array}{r}6.283\approx 2\pi \end{array}$ . A conjecture would be that the circumference of a circle with radius 1 unit is $\begin{array}{r}2\pi \text{un}\end{array}$ .
  ::例2、例3和例4的周界接近6.2832。一个假设是,半径1单位的圆圈环绕是2 un。

  Summary

  播放段落 A circle is the set of all points that are the same distance away from a specific point, called the center. ::一个圆是所有点的一组,这些点与特定点的距离相同,称为中点。 播放段落 The circumference of a circle is $\begin{array}{r}C=2\pi r=\pi d.\end{array}$   ::圆环环为C=2rd。 播放段落 The area of a circle is $\begin{array}{r}A=\pi r^2\end{array}$   ::圆区域为 Ar2 播放段落 To find the area of a polygon: 播放段落 break the polygon into congruent triangles ::将多边形折断为相容三角形 播放段落 find the area of one triangle and multiply that by the number of sides ::查找一个三角形区域,乘以边数 ::要找到多边形的区域, 需要找到多边形的区域: 将多边形破碎成相似的三角形, 找到一个三角形的区域, 并乘以边数 播放段落 To find the perimeter of a polygon: 播放段落 break the polygon into congruent triangles ::将多边形折断为相容三角形 播放段落 find the base of one triangle and multiply that by the number of sides ::查找一个三角形的基底,乘以边数 ::找到多边形的周边:将多边形破碎成相似的三角形,找到一个三角形的底部,乘以边数

  ---

  播放段落

  Review
  ::审查审查审查审查

  播放段落

  Consider a regular $\begin{array}{r}n\end{array}$ -gon inscribed in a circle with radius 1 unit for questions 1-8.
  ::考虑将问题1-8标在圆形内、半径1单位的普通正方形正方形。

  播放段落

  1. What's the measure of the angle between the radius and the height of one triangle in terms of $\begin{array}{r}n\end{array}$ ?
  ::1. 圆半径与一个三角形高度之间的角以 n 表示的度量是多少?

  播放段落

  2. What's the length of the base of one triangle in terms of sine and $\begin{array}{r}n\end{array}$ ?
  ::2. 从正弦和正弦的角度来说,一个三角形的基底长度是多少?

  播放段落

  3. What's the height of one triangle in terms of cosine and $\begin{array}{r}n\end{array}$ ?
  ::3. 一个三角形以松和N的高度是多少?

  播放段落

  4. What's the area of one triangle in terms of sine, cosine, and $\begin{array}{r}n\end{array}$ ?
  ::4. 一个三角形的面积从正弦、共弦和n方面来说是多少?

  播放段落

  5. What's the area of the polygon in terms of sine, cosine, and $\begin{array}{r}n\end{array}$ ?
  ::5. 就正弦、共弦和n而言,多边形的面积是多少?

  播放段落

  6. What's the perimeter of the polygon in terms of sine, cosine, and $\begin{array}{r}n\end{array}$ ?
  ::6. 多边形的边缘,从正弦、共弦和n的角度来看是多少?

  播放段落

  7. Let $\begin{array}{r}n=10,000\end{array}$ . What is the area of the polygon? What is the perimeter of the polygon? Use your calculator and your answers to #6 and #7.
  ::7. n=10 000。多边形的区域是什么?多边形的周界是什么?使用你的计算器和对#6和#7的答复。

  播放段落

  8. Let $\begin{array}{r}n=1,000,000\end{array}$ . What is the area of the polygon? What is the perimeter of the polygon? Are you convinced that the area of a circle with radius 1 unit is $\begin{array}{r}\pi \end{array}$ and the circumference of a circle with radius 1 unit is $\begin{array}{r}2\pi \end{array}$ ?
  ::8. n=1 000 000。多边形的区域是什么?多边形的周界是什么?多边形的周界是什么?你是否确信圆圆一半径一单元的区域是__;圆一半径一单元的环形是2__?

  播放段落

  9. Explain why the area of a regular polygon inscribed in a circle with radius 1 unit gets closer to $\begin{array}{r}\pi \end{array}$ as the number of sides increases.
  ::9. 解释为什么在圆形中标有圆形、半径1单位的正多边形区域随着边数的增加而接近 。

  播放段落

  10. Explain why the perimeter of a regular polygon inscribed in a circle with radius 1 unit gets closer to $\begin{array}{r}2\pi \end{array}$ as the number of sides increases.
  ::10. 解释为什么在圆形上标有圆形、半径1单位的常规多边形的周界随着边数的增加而接近2。

  播放段落

  11. Use similarity and the fact that the circumference of a circle with radius 1 unit is $\begin{array}{r}2\pi \end{array}$ to explain why the formula for the circumference of a circle with radius $\begin{array}{r}r\end{array}$ is $\begin{array}{r}2\pi r\end{array}$ .
  ::11. 使用相似之处,而且圆圆半径1单位的环绕为2,以此解释为什么圆半径r圆的环绕公式为2r。

  播放段落

  12. A circle with radius 3 units is transformed into a circle with radius 5 units. What is the ratio of their areas? What is the ratio of their circumferences?
  ::12. 半径3单位的圆圆被转换成半径5单位的圆圆。其区域的比例是多少?其环形的比例是多少?

  播放段落

  13. The ratio of the areas of two circles is $\begin{array}{r}25:4\end{array}$ . The radius of the smaller circle is 2 units. What's the radius of the larger circle?
  ::13. 两个圆圈区域的比例是25:4,小圆圈的半径是2个单位。大圆圈的半径是多少?

  播放段落

  14. The ratio of the areas of two circles is $\begin{array}{r}25:9\end{array}$ . The radius of the larger circle is 10 units. What's the radius of the smaller circle?
  ::14. 两个圆圈区域的比例是 25:9. 大圆圈的半径是 10 个单位。小圆圈的半径是 多少?

  播放段落

  15. The ratio of the areas of two circles is $\begin{array}{r}5:4\end{array}$ . The radius of the larger circle is 8 units. What's the circumference of the smaller circle?
  ::15. 两个圆圈的面积比例是5:4,大圆圈的半径是8个单位。小圆圈的宽度是多少?

  播放段落

  16. The radius of a circular helicopter landing pad is increased by 10 feet. Determine the simplified expression for the increase in area. What is the increase in the circumference of the landing pads?
  ::16. 圆形直升机起降坪的半径增加10英尺,确定增加面积的简化表达方式。

  播放段落

  17. An octagonal hot tub seats 8 people, with each person leaning against the 4' side of the octagon. Explain how you would determine the area of the top of the octagon in order to construct a cover for the hot tub.
  ::17. 八角热浴缸座8人,每人靠八角热浴缸的4面,解释如何确定八角热浴缸顶部的面积,以便为热浴缸盖盖。

  播放段落

  18. A circular plate has a diameter of 10 inches. Two cookies, each with a radius of 1.1 inches, are on the plate. Explain how to determine what percentage of the plate's area is not covered by the cookies.
  ::18. 圆形板直径为10英寸,盘子上有两块饼干,每块半径为1.1英寸,解释如何确定板子面积中哪些百分比没有被饼干覆盖。

  播放段落

  Review (Answers)
  ::审查(答复)

  播放段落

  Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
  ::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键 。