Course: 8.3 中央角和弦-interactive

Section outline

Select section General

Collapse Expand
General

Collapse all Expand all
- Select activity 新闻通告
  
  新闻通告 Forum

中角和弦

A central angle for a circle is an angle with its vertex at the center of the circle and with endpoints $\begin{aligned} B \end{aligned}$ and $\begin{aligned} C \end{aligned}$ located on a circle's .
::圆的中角是圆的中心角,其顶点在圆的中心,端点B和C位于圆的圆上。

In the circle above, $\begin{aligned} A \end{aligned}$ is the center and $\begin{aligned} ∠ B A C \end{aligned}$ is a central angle. Notice that the central angle meets the circle at two points ( $\begin{aligned} B \end{aligned}$ and $\begin{aligned} C \end{aligned}$ ), dividing the circle into two sections. Each of circle portions is called an arc . The smaller arc (smaller than the semicircle) is called the minor arc , and is considered the arc that is intercepted by the central angle. The larger of the two arcs is called the major arc .
::在上方的圆圈中, A 是中心, 并且 {BAC 是一个中心角度。请注意, 中心角度在两个点( B和 C) 与圆形相匹配, 将圆形分为两个部分。圆形的每个部分称为弧。较小的弧( 比半圆弧小的) 被称为小弧, 并被视为被中心角度截取的弧。两个弧中的大弧称为大弧。

The minor arc below is named $\begin{aligned} \hat{B C} \end{aligned}$ . Notice that $\begin{aligned} B \end{aligned}$ and $\begin{aligned} C \end{aligned}$ are the endpoints of the arc and there is an arc symbol above the letters indicating that you are referring to an arc.
::下面的次要弧名为 BCQ。请注意 B和 C 是弧的终点, 在字母上方有一个弧符号, 表示您指的是弧。

The major arc below is named $\begin{aligned} \hat{B D C} \end{aligned}$ . When naming a major arc you should use three letters so that it is clear you are referring to the larger portion of the circle.
::下面的主要弧名为 BDC 。当命名一个大弧时, 您应该使用三个字母, 这样您可以清楚地看到您指的是圆圈的较大部分。

Arcs can be measured in degrees just like angles. In general, the degree measure of a minor arc is equal to the measure of the central angle that intercepts it . Because there are $\begin{aligned} 360^{\circ} \end{aligned}$ in a circle, the sum of the measures of a minor arc and its corresponding major arc will be $\begin{aligned} 360^{\circ} \end{aligned}$ .
::弧可以用与角度相同的度量度来测量弧。一般来说, 小弧的度量等于截取弧的中角的度量。因为圆圈里有 360 , 小弧的度量及其相应的大弧的度量总和将是 360 。

A chord of a circle is a straight line segment whose endpoints both lie on the circle. If a chord passes through the center of the circle then it is a diameter . In the circle below, $\begin{aligned} \bar{C E} \end{aligned}$ is a chord.
::一个圆的和弦是一个直线段,其终点都位于圆上。如果一个和弦穿过圆的中心,则是一个直径。在下面的圆中,CE是一个和弦。

Each chord has a corresponding arc. $\begin{aligned} \bar{C E} \end{aligned}$ is a chord and $\begin{aligned} \hat{C E} \end{aligned}$ is an arc.
::每个和弦都有相应的弧。和弦是和弦,和弦是弧。

INTERACTIVE

Central Angles and Chords

Move the red points to explore the different types of arcs that can be found in a circle.
::移动红点以探索圆形中可以找到的不同类型的弧。

In the interactive above, if $\begin{aligned} D \end{aligned}$ was not on the circle, we would not be able to tell the difference between $\begin{aligned} \hat{B C} \end{aligned}$ and $\begin{aligned} \hat{B D C} \end{aligned}$ . There are $\begin{aligned} 360^{\circ} \end{aligned}$ in a circle, where a semicircle is half of a circle, or $\begin{aligned} 180^{\circ} \end{aligned}$ . $\begin{aligned} m ∠ E F G = 180^{\circ} \end{aligned}$ , because it is a straight angle , so $\begin{aligned} m \hat{E H G} = 180^{\circ} \end{aligned}$ and $\begin{aligned} m \hat{E J G} = 180^{\circ} \end{aligned}$ .
::在上述互动中,如果D不在圆圈内,我们无法辨别BC和BDC之间的差别。在圆圈内,有360半圆,半圆半圆,或180.mEFG=180,因为它是一个直角,所以是mEHG180和MEJG180。

Let's take a look at a few problems involving central angles and chords.
::让我们来看看几个问题涉及到中心角度和和弦。

1. Find $\begin{aligned} m ∠ C A E \end{aligned}$ and $\begin{aligned} m \hat{C D E} \end{aligned}$ .
::1. 寻找mCAE和mCDE。

The degree measure of a minor arc is equal to the measure of the central angle that intercepts it. Therefore, $\begin{aligned} m ∠ C A E = 140^{\circ} \end{aligned}$ . A full circle is $\begin{aligned} 360^{\circ} \end{aligned}$ , so
::小弧的度量等于截取该弧的中心角的度量。因此, mCAE=140 。一个整圆是 360 , 所以是 360 。

$\begin{aligned} m \hat{C D E} & = 360^{\circ} - ∠ C A E \\ = 360^{\circ} - 140^{\circ} \\ = 220^{\circ} \end{aligned}$
::mCDE360CAE=360140220

2. Prove that two chords are congruent if and only if their corresponding arcs are congruent.
::2. 证明两个和弦是一致的,如果而且只有在相应的和弦是一致的时才如此。

This statement has two parts that you must prove.
::本陈述分为两部分,你们必须证明。

If two arcs are congruent then their corresponding chords are congruent.
::如果两个弧是一致的,那么它们相应的和弦是一致的。

If two chords are congruent then their corresponding arcs are congruent.
::如果两个和弦是一致的,那么它们相应的弧是一致的。

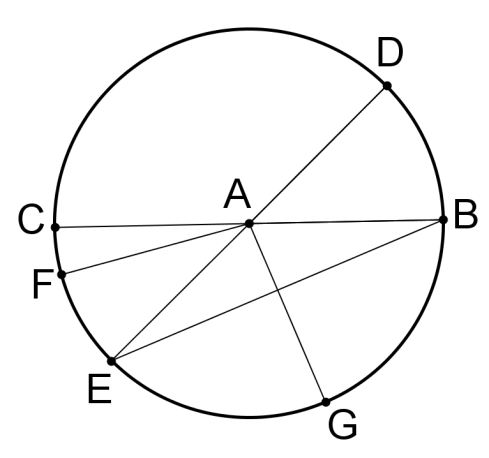
Both statements can be proved by finding . Consider the circle below with center $\begin{aligned} A \end{aligned}$ .
::两种语句都可以通过找到来证明。请考虑下面的圆和中心 A 。

Start by proving statement #1. Let there be two arcs $\begin{aligned} \hat{C D} \end{aligned}$ and $\begin{aligned} \hat{F E} \end{aligned}$ such that $\begin{aligned} \hat{C D} ≅ \hat{F E} \end{aligned}$ . This would imply that $\begin{aligned} m \hat{C D} = m \hat{F E} \end{aligned}$ .
::首先证明声明 #1. 让两个弧 CD 和 FE 来证明CD\ FE。这意味着 mCD\ mFE 。

Join $\begin{aligned} \bar{C A}, \bar{D A}, \bar{E A} \end{aligned}$ and $\begin{aligned} \bar{F A} \end{aligned}$ as shown in the figure.
::加入CA,DA,EA,AFA,如图所示。

	Statements	Reasons
In $\begin{aligned} △ A C D \end{aligned}$ and $\begin{aligned} △ A F E \end{aligned}$
	$\begin{aligned} ∠ C A D = ∠ F A E \end{aligned}$	Measure of an arc is the same as the measure of its corresponding angle.
	$\begin{aligned} \bar{C A} = \bar{F A} \end{aligned}$	Radii of the same circle
	$\begin{aligned} \bar{D A} = \bar{E A} \end{aligned}$	Radii of the same circle
	$\begin{aligned} △ C A D ≅ △ F A E \end{aligned}$	By $\begin{aligned} ≅ \end{aligned}$
	$\begin{aligned} \bar{C D} ≅ \bar{F E} \end{aligned}$	By

Now prove the converse (statement #2). Let there be two chords $\begin{aligned} \bar{C D} ≅ \bar{F E} \end{aligned}$ .
::现在证明相反的一面(声明2),

Join $\begin{aligned} \bar{C A}, \bar{D A}, \bar{E A} \end{aligned}$ and $\begin{aligned} \bar{F A} \end{aligned}$ as shown in the figure.
::加入CA,DA,EA,AFA,如图所示。

	Statements	Reasons
In $\begin{aligned} △ A C D \end{aligned}$ and $\begin{aligned} △ A F E \end{aligned}$
	$\begin{aligned} \bar{C D} = \bar{F E} \end{aligned}$	Given
	$\begin{aligned} \bar{C A} = \bar{F A} \end{aligned}$	Radii of the same circle
	$\begin{aligned} \bar{D A} = \bar{E A} \end{aligned}$	Radii of the same circle
	$\begin{aligned} △ C A D ≅ △ F A E \end{aligned}$	By $\begin{aligned} ≅ \end{aligned}$
	$\begin{aligned} ∠ C A D ≅ ∠ F A E \end{aligned}$	By CPCTC

This implies that the arcs intercepted by these angles are congruent and therefore $\begin{aligned} \hat{C D} ≅ \hat{F E} \end{aligned}$ .
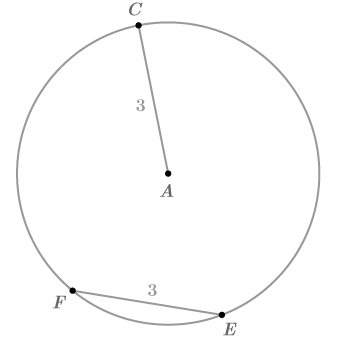
::这意味着被这些角度拦截的弧是相同的,因此是CDFE。

INTERACTIVE

Central Angles and Chords

Move the red points to change the congruent chords on this circle.
::移动红点以更改此圆的和弦。

3. $\begin{aligned} A \end{aligned}$ is the center of the circle below. Find the shortest distance from $\begin{aligned} A \end{aligned}$ to $\begin{aligned} \bar{E F} \end{aligned}$ .
::3. A是以下圆圈的中心,找到从A到EF的最短距离。

Circle with center A, radii AC and AE of length 3, illustrating a 30-60-90 triangle.

The shortest distance from $\begin{aligned} A \end{aligned}$ to $\begin{aligned} \bar{E F} \end{aligned}$ will be the length of a segment from $\begin{aligned} A \end{aligned}$ to $\begin{aligned} \bar{E F} \end{aligned}$ that is perpendicular to $\begin{aligned} \bar{E F} \end{aligned}$ . Because $\begin{aligned} A \end{aligned}$ is the center of the circle, $\begin{aligned} \bar{A C} \end{aligned}$ is a radius and thus the length of any radius will be 3 units. Draw two radii from $\begin{aligned} A \end{aligned}$ to $\begin{aligned} E \end{aligned}$ and $\begin{aligned} A \end{aligned}$ to $\begin{aligned} F \end{aligned}$ . Also draw a segment from $\begin{aligned} A \end{aligned}$ to $\begin{aligned} \bar{E F} \end{aligned}$ that is perpendicular to $\begin{aligned} \bar{E F} \end{aligned}$ .
::A 到 EF 之间的最短距离是 A 到 EF 之间的一个段段的长度。因为 A 是圆的中心, AC 是半径, 因此任何半径的长度为 3 个单位。从 A 到 E 和 A 到 F 绘制两个。另外, 从 A 到 EF 也绘制一个段。

$\begin{aligned} △ A F E \end{aligned}$ is an because it has three sides of length 3. This means that $\begin{aligned} m ∠ A F D = 60^{\circ} \end{aligned}$ and $\begin{aligned} △ A F D \end{aligned}$ is a 30-60-90 triangle . According to the 30-60-90 pattern,
::“AFE”是因为它有三对三的长度3。这意味着“MAFD=60”和“AFD”是30-60-90三角形。根据30-60-90模式,

$\begin{aligned} A D = A F \sin 60^{\circ} = \frac{3 \sqrt{3}}{2} . \end{aligned}$
::AD=AFsin60332。

Examples
::实例实例实例实例

Example 1
::例1

Radius $\begin{aligned} \bar{A D} \end{aligned}$ bisects $\begin{aligned} ∠ B A C \end{aligned}$ in the circle below. How does $\begin{aligned} \bar{A D} \end{aligned}$ relate to chord $\begin{aligned} \bar{B C} \end{aligned}$ ? Prove your ideas.
::{\fn黑体\fs22\bord1\shad0\3aHBE\4aH00\fscx67\fscy66\2cHFFFFFF\3cH808080}

Two possible conjectures are that $\begin{aligned} \bar{A D} \end{aligned}$ bisects $\begin{aligned} \bar{B C} \end{aligned}$ and $\begin{aligned} \bar{A D} \end{aligned}$ is perpendicular to $\begin{aligned} \bar{B C} \end{aligned}$ . Both of these conjectures can be proved by first proving that $\begin{aligned} △ A B E ≅ △ A C E \end{aligned}$ .
::两种可能的假设是,AD's两部分BC和AD's与BC有关。这两个假设可以通过首先证明`ABE'ACE来证明。

To prove that $\begin{aligned} △ A B E ≅ △ A C E \end{aligned}$ , first note that $\begin{aligned} \bar{A B} \end{aligned}$ and $\begin{aligned} \bar{A C} \end{aligned}$ are both radii of the circle, and therefore $\begin{aligned} \bar{A B} ≅ \bar{A C} \end{aligned}$ . Also note that $\begin{aligned} \bar{A E} ≅ \bar{A E} \end{aligned}$ by the reflexive property. Since it was assumed that $\begin{aligned} \bar{A D} \end{aligned}$ bisects $\begin{aligned} ∠ B A C \end{aligned}$ , $\begin{aligned} ∠ B A E ≅ ∠ C A E \end{aligned}$ . $\begin{aligned} △ A B E ≅ △ A C E \end{aligned}$ by $\begin{aligned} S A S ≅ \end{aligned}$ .
::证明ABEACE, 首先指出AB和AC都是圆的弧线, 因此AB AC。也注意到AE AE是反向财产。因为SAS假定AD是AD的两部分 ABAC, ABAECAE。 ABEACE ABEACE ABEACE ABEACE ABEACE是SAS的。

Because $\begin{aligned} △ A B E ≅ △ A C E \end{aligned}$ , $\begin{aligned} \bar{B E} ≅ \bar{E C} \end{aligned}$ because they are corresponding parts. Therefore, $\begin{aligned} \bar{A D} \end{aligned}$ bisects $\begin{aligned} \bar{B C} \end{aligned}$ . Also because $\begin{aligned} △ A B E ≅ △ A C E \end{aligned}$ , $\begin{aligned} ∠ C E A ≅ ∠ B E A \end{aligned}$ because they are corresponding parts. $\begin{aligned} ∠ C E A \end{aligned}$ and $\begin{aligned} ∠ B E A \end{aligned}$ are supplementary because they form a line . Therefore, $\begin{aligned} m ∠ C E A = m ∠ B E A = 90^{\circ} \end{aligned}$ and $\begin{aligned} \bar{A D} \end{aligned}$ is perpendicular to $\begin{aligned} \bar{B C} \end{aligned}$ .
::“ABEACE,BECE”是因为它们是相应的部分。因此,AD是BC的两部分。同样,因为ABEACE,CEABEA是相应的部分。“CEA”和“BEA”是补充性的,因为它们组成了一条线。因此,MCEA=mBEA=90,AD是BC的内在部分。

This means that if a radius bisects a central angle, then it is the perpendicular bisector of the related chord.
::这意味着,如果半径将一个中心角度分为两部分,那么它就是相关和弦的直角两部分。

Example 2
::例2

In the circle below, diameters $\begin{aligned} \bar{E B} \end{aligned}$ and $\begin{aligned} \bar{C F} \end{aligned}$ are perpendicular and $\begin{aligned} m ∠ E A D = 30^{\circ} \end{aligned}$
::在以下圆形中,直径EB'和CF'是垂直直径和MEAD=30

i) Find $\begin{aligned} m \hat{B C} \end{aligned}$ .
:一) 寻找 mBC_。

$\begin{aligned} \bar{E B} \end{aligned}$ and $\begin{aligned} \bar{C F} \end{aligned}$ are perpendicular. This means that $\begin{aligned} m ∠ C A B = 90^{\circ} \end{aligned}$ and therefore $\begin{aligned} m \hat{B C} = 90^{\circ} \end{aligned}$
::EB和CF是垂直的这意味着MCAB=90 因此MBC=90

ii) Find $\begin{aligned} m \hat{D F} \end{aligned}$ in the circle.
:二) 在圆圈中查找 mDF。

$\begin{aligned} m ∠ E A F = 90^{\circ} \end{aligned}$ because $\begin{aligned} ∠ E A F \end{aligned}$ and $\begin{aligned} ∠ C A B \end{aligned}$ are and are therefore congruent. This means that
::mEAF=90,因为EAF和CAB是并因此是一致的。这意味着:

$\begin{aligned} m ∠ D A F \end{aligned}$ $\begin{aligned} = m ∠ E A F - m ∠ E A D \end{aligned}$
::mDAF=mEAF-mEAD

$\begin{aligned} = 90^{\circ} - 30^{\circ} = 60^{\circ} \end{aligned}$ and therefore $\begin{aligned} m \hat{D F} = 60^{\circ} \end{aligned}$ .
::90+30+60+因此MDF+60+。

iii) Find $\begin{aligned} m ∠ B A D \end{aligned}$ in the circle.
:三) 在圆圈中找到 mBAD。

$\begin{aligned} m ∠ B A F = 90^{\circ} \end{aligned}$ because it is supplementary with $\begin{aligned} ∠ B A C \end{aligned}$ . $\begin{aligned} m ∠ B A D = m ∠ B A F + m ∠ D A F \end{aligned}$ . Therefore, $\begin{aligned} m ∠ B A D = 90^{\circ} + 60^{\circ} = 150^{\circ} \end{aligned}$ .
::mBAF=90 ' 因为它是补充的 'BAC. mBAD=mBAF+mDAF. 因此, mBAD=9060150\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\BABAF\\\\\\BAF\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\BBBBBBBBBBBBBBBBBBBBBB

CK-12 PLIX: Chords and Central Angle Arcs
::CK-12 PLIX: 弦和中央角弧

Summary

A central angle for a circle is an angle with its vertex at the center of the circle and endpoints located on a circle's circumference.
::圆的中角是一个角,其顶点位于圆的中心,终点位于圆的环形上。

An arc is a section of the circumference of a circle.
- A major arc is greater than 180 ^o .
  ::大弧大于180度。
- A minor arc if it is less than 180 ^o
  ::如果小于180o,则小弧值为180o
::弧是圆环环的一部分。大弧大于180o。小弧小弧小于180o

A chord of a circle is a straight line segment whose endpoints both lie on the circle.
::圆的和弦是一个直线段,其终点都位于圆上。

Review
::审查审查审查审查

1. Draw an example of a central angle and its intercepted arc .
::1. 举一个中心角及其截断弧的例子。

2. What's the relationship between a central angle and its intercepted arc?
::2. 中央角度与被拦截的弧之间有什么关系?

3. Draw an example of a chord.
::3. 举一个和弦的例子。

4. A chord that passes through the center of the circle is called a _______________.
::4. 横穿圆圈中心的和弦称为。

In the circle below, $\begin{aligned} \bar{C B} \end{aligned}$ and $\begin{aligned} \bar{E D} \end{aligned}$ are diameters, $\begin{aligned} \bar{A G} \end{aligned}$ bisects $\begin{aligned} ∠ E A B \end{aligned}$ , $\begin{aligned} m ∠ D A B = 50^{\circ} \end{aligned}$ and $\begin{aligned} m ∠ C A F = 20^{\circ} \end{aligned}$ . Use this circle for #5-#9.
::CB'和ED'是直径, AG'两部分为“EAB”, mDAB=50和 mCAF=20。使用这个圆来表示#5-9。

5. Find $\begin{aligned} m \hat{F E} \end{aligned}$ .
::5. 寻找MFE。

6. Find $\begin{aligned} m \hat{C D} \end{aligned}$ .
::6. 寻找 mCD。

7. Find $\begin{aligned} m ∠ E A G \end{aligned}$ .
::7. 寻找MAEAG。

8. Find $\begin{aligned} m \hat{G B} \end{aligned}$ .
::8. 寻找 mGB_。

9. How is $\begin{aligned} \hat{E B} \end{aligned}$ related to $\begin{aligned} \bar{A G} \end{aligned}$ ?
::9. EBA与AG的关系如何?

10. Prove that when a radius bisects a chord, it is perpendicular to the chord. Use the picture below and prove that $\begin{aligned} m ∠ A F D = 90^{\circ} \end{aligned}$ .

::10. 证明半径两切为和弦时,与和弦垂直。

11. Prove that when a radius is perpendicular to a chord it bisects the chord. Use the picture below and prove that $\begin{aligned} \bar{E F} ≅ \bar{F D} \end{aligned}$ .
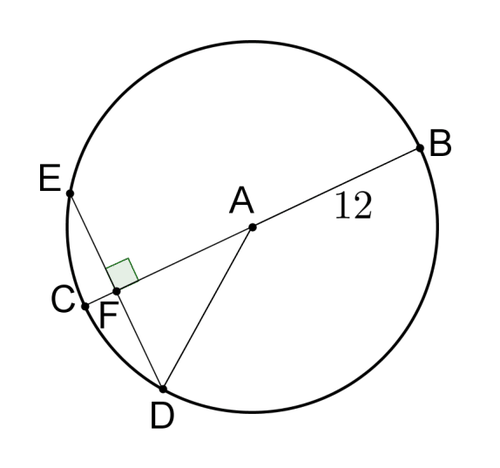
::11. 证明当半径与一和弦垂直时,半径将和弦分为两部分,使用下面的图片证明EF {FD}。

In the circle below with center $\begin{aligned} A \end{aligned}$ , $\begin{aligned} A B = 12 \end{aligned}$ and $\begin{aligned} D E = 16 \end{aligned}$ .
::以A、AB=12和DE=16为中心,在下方圆形。

12. Find $\begin{aligned} D F \end{aligned}$ .
::12. 寻找DF。

13. Find $\begin{aligned} A C \end{aligned}$ .
::13. 寻找AC。

14. Find $\begin{aligned} A F \end{aligned}$ .
::14. 查找适应基金。

15. Find $\begin{aligned} C F \end{aligned}$ .
::15. 找到CF。

16. Prove that no matter where a point is placed on the arc of a semicircle, the angle formed will always be a right angle.
::16. 证明无论在半圆圈弧上放一个点,形成的角度始终是一个正确的角度。

17. Using a standard analogue clock, explain how to determine the measure of the angle formed between the two hands at three different times during the day.
::17. 使用标准的模拟时钟,解释如何在白天三次不同时间确定两手之间形成角的度量。

18. In the diagram below, explain why $\begin{aligned} △ A O C and △ B O C \end{aligned}$ are isosceles. What can be deduced about the relationship between $\begin{aligned} ∠ A O B and ∠ A C B ? \end{aligned}$
::18. 在下图中,请解释为什么AOC和BOC是等离子体,对于AOB和ACB之间的关系可以推断出什么?

Review (Answers)
::审查(答复)

Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键。

Section outline

General

中角和弦

Examples ::实例实例实例实例

Example 1 ::例1

Example 2 ::例2

CK-12 PLIX: Chords and Central Angle Arcs ::CK-12 PLIX: 弦和中央角弧

Review ::审查审查审查审查