8.4 说明的角-interactive

Section outline

• Select section General

  Collapse Expand

  General

  Collapse all Expand all

  • Select activity 新闻通告

    

    新闻通告 Forum
• Select section 归属角

  Collapse Expand

  归属角

  播放段落

  An inscribed angle is an angle formed by two chords in a circle which have a common endpoint . This common endpoint forms the vertex of the inscribed angle. The other two endpoints define what we call an intercepted arc on the circle. Below, $\begin{align*}\angle CED\end{align*}$ is an inscribed angle.
  ::刻入角是圆中两个和弦形成的一个角,圆中有一个共同的端点。这个共同的端点形成刻入角的顶点。另外两个端点定义了我们在圆上所谓的截取弧。下面, CED是一个刻入角。

  播放段落

  Inscribed angles are inscribed in arcs. You can say that $\begin{align*}\angle CED\end{align*}$ is inscribed in $\begin{align*}\widehat{CD}\end{align*}$ . You can also say that $\begin{align*}\angle CED\end{align*}$ intercepts $\begin{align*}\widehat{CD}\end{align*}$ .
  
  ::给定角度被刻入弧形。 您可以说 CED 被刻入 CDQ。 您也可以说 CED 截取 CDQQ 。

  播放段落

  The measure of an inscribed angle is always half the measure of the arc it intercepts. You will prove and then use this theorem in the problems below.
  ::刻入角的测量量始终是它截获的弧量的一半。 您可以在下面的问题中证明并使用这个理论 。

  播放段落

  1. Consider the circle below with center at point $\begin{align*}A\end{align*}$ . Prove that $\begin{align*}m \angle AEC = \frac{1}{2} m \angle CAD = \frac{1}{2} m \widehat{CD}\end{align*}$ .
  ::1. 考虑下方圆,以A点为中心。证明 mAEC=12mCAD=12mCD。

  	Statements	Reasons
  In $\begin{align*}\triangle CAE\end{align*}$ ,
  	$\begin{align*}m \angle ACE\end{align*}$ $\begin{align*}=\end{align*}$ $\begin{align*}m \angle AEC\end{align*}$	$\begin{align*}\overline{CA} = \overline{EA}\end{align*}$ (radii of the same circle)
  	$\begin{align*}m \angle CAD = m \angle ACE + m \angle AEC\end{align*}$	Ext $\begin{align*}\angle\end{align*}$ of a $\begin{align*}\triangle\end{align*}$ = sum of int. opp angles
  $\begin{align*}\Rightarrow\end{align*}$	$\begin{align*}m \angle CAD = m \angle AEC + m \angle AEC = 2 m \angle AEC = 2 m \angle ACE\end{align*}$
  $\begin{align*}\Rightarrow\end{align*}$	$\begin{align*}\frac{1}{2} m \angle CAD = m \angle AEC\end{align*}$
  	$\begin{align*}m \angle CAD \end{align*}$ $\begin{align*}=\end{align*}$ $\begin{align*}m \widehat{CD}\end{align*}$	Central angle has the same measure as its intercepted arc
  	$\begin{align*}\frac{1}{2} m \widehat{CD} = m \angle AEC\end{align*}$	By substitution

  播放段落

  This proves that when an inscribed angle passes through the center of a circle, its measure is half the measure of the arc it intercepts.
  ::这证明当一个刻着的角穿过圆的中心时, 它的量度是它拦截的弧的量度的一半。

  播放段落

  2. Use the result from the previous problem to prove that $\begin{align*}m \angle CED\end{align*}$ $\begin{align*}= \frac{1}{2}\end{align*}$ $\begin{align*}m \widehat{CD}\end{align*}$ .
  ::2. 使用上一个问题的结果来证明 mCED=12mCD。

  播放段落

  Draw a diameter through points $\begin{align*}E\end{align*}$ and $\begin{align*}A\end{align*}$ .
  ::通过点E和A绘制直径。

  播放段落

  From #1, you know that $\begin{align*}m \angle FEC\end{align*}$ $\begin{align*}= \frac{1}{2}\end{align*}$ $\begin{align*}m \angle FAC\end{align*}$ .
  ::从1,你知道MFEC=12mFAC。

  播放段落

  You also know that $\begin{align*}m \angle FED\end{align*}$ $\begin{align*}= \frac{1}{2}\end{align*}$ $\begin{align*}m \angle FAD\end{align*}$ .
  ::你也知道MFED=12mFAD。

  播放段落

  Because $\begin{align*}m \angle FED = m \angle FEC + m \angle CED\end{align*}$ , by substitution $\begin{align*}\frac{1}{2} m \angle FAD = \frac{1}{2} m \angle FAC + m \angle CED\end{align*}$ . This means $\begin{align*}m \angle CED = \frac{1}{2} (m \angle FAD - m \angle FAC)\end{align*}$ . $\begin{align*}m \angle FAD - m \angle FAC = m \angle CAD\end{align*}$ , so $\begin{align*}m \angle CED = \frac{1}{2} m \angle CAD\end{align*}$ .
  ::因为MFED=mFEC+mCED,代号:12mFAD=12mFAC+mCED。这意味着mCED=12(mFAD-mFAC)。mFAD-mFAC=mCAD,所以mCED=12mCAD。

  播放段落

  Because $\begin{align*}m \angle CAD \end{align*}$ $\begin{align*}=\end{align*}$ $\begin{align*}m \widehat{CD}\end{align*}$ , $\begin{align*}m \angle CED = \frac{1}{2} m \widehat{CD}\end{align*}$ .
  ::因为MCAD=mCD,MCED=12mCD。

  播放段落

  This proves in general that the measure of an inscribed angle is half the measure of its intercepted arc.
  ::这一般证明,一个刻入角的测量量是其被拦截弧的测量量的一半。

  播放段落

  Central Angle Theorem
  ::中心角定理

  播放段落

  Drag the point $\begin{align*}P\end{align*}$ , $\begin{align*}Q\end{align*}$ or $\begin{align*}R\end{align*}$ on the of the circle and observe how the central angle is always twice the inscribed angle.
  ::在圆上拖曳点P、Q或R,并观察中角如何始终是刻入角的两倍。

  播放段落

  Now let's find the measure of an angle.
  ::现在让我们找到一个角度的量度。

  播放段落

  Find $\begin{align*}m \angle CED\end{align*}$ .
  ::寻找mCED。

  播放段落

  Notice that both $\begin{align*}\angle CED\end{align*}$ and $\begin{align*}\angle CBD\end{align*}$ intercept $\begin{align*}\widehat{CD}\end{align*}$ . This means that their measures are both half the measure of $\begin{align*}\widehat{CD}\end{align*}$ , so their measures must be equal. $\begin{align*}m \angle CED=38^\circ\end{align*}$ .
  ::请注意,“CED”和“CBD”都拦截CD__。这意味着,它们的措施是CD__的一半,因此它们的措施必须是相等的。“MCED=38”。

  ---

  播放段落

  Examples
  ::实例实例实例实例

  播放段落

  Example 1
  ::例1

  播放段落

  Point $\begin{align*}A\end{align*}$ is the center of the circle below. What can you say about $\begin{align*}\triangle CBD\end{align*}$ ?
  ::A点是以下圆圈的中心。您对“CBD”有什么看法?

  播放段落

  If point $\begin{align*}A\end{align*}$ is the center of the circle, then $\begin{align*}\overline{CB}\end{align*}$ is a diameter and it divides the circle into two equal halves. This means that $\begin{align*}m\widehat{CB}=180^\circ\end{align*}$ . $\begin{align*}\angle CDB\end{align*}$ is an inscribed angle that intercepts $\begin{align*}\widehat{CB}\end{align*}$ , so its measure must be half the measure of $\begin{align*}\widehat{CB}\end{align*}$ . Therefore, $\begin{align*}m \angle CDB=90^\circ\end{align*}$ and $\begin{align*} \triangle CBD\end{align*}$ is a right triangle .
  ::如果 A 点是圆的中心, 那么 CB 是直径, 并且将圆分为两等分。 这意味着 mCB\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\CBDBDD\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\

  播放段落

  In general, if a triangle is inscribed in a semicircle then it is a right triangle.
  ::一般而言,如果三角形被刻在半圆圈内,它就是右三角形。

  播放段落

  In Example #2 and #3, you will use the circle below to prove that when two chords intersect inside a circle, the products of their segments are equal.
  ::在例2和例3中,您将使用下面的圆来证明 当两个和弦在圆内交叉时, 其区段的产品是相等的 。

  播放段落

  Example 2
  ::例2

  播放段落

  Prove that $\begin{align*}\triangle EFC \sim \triangle BFD\end{align*}$ . Hint: Look for congruent angles!
  ::寻找一致的角度!

  播放段落

  $\begin{align*}\angle CED \cong \angle CBD\end{align*}$ because both are inscribed angles that intercept the same arc ( $\begin{align*}\widehat{CD}\end{align*}$ ). $\begin{align*}\angle EFC \cong \angle BFD \end{align*}$ because they are . Therefore, $\begin{align*}\triangle EFC \sim \triangle BFD\end{align*}$ by $\begin{align*}AA \sim\end{align*}$ .
  ::“CEDCBD”因为两者都是刻着拦截同一弧的角(CD)。”“EFCBFD”因为它们是。因此,“EFCBFD”是AA。

  播放段落

  Example 3
  ::例3

  播放段落

  Prove that $\begin{align*}EF \cdot FD = BF \cdot FC\end{align*}$ .
  ::证明FEF=FFFC。

  播放段落

  Because $\begin{align*}\triangle EFC \sim \triangle BFD\end{align*}$ , its corresponding sides are proportional. This means that $\begin{align*}\frac{EF}{BF}\end{align*}$ $\begin{align*}=\end{align*}$ $\begin{align*}\frac{FC}{FD}\end{align*}$ . Multiply both sides of the equation by $\begin{align*}BF \cdot FD\end{align*}$ and you have $\begin{align*}EF \cdot FD = BF \cdot FC\end{align*}$ . This proves that in general, when two chords intersect inside a circle, the products of their segments are equal.
  ::由于 EFC BFD, 其对应面是正比的。 这意味着 FFBF = FFFD 。 乘以 BFFFD 和你有 EFZFD = BFFFC 方程的两边。 这证明, 一般来说, 当两根和弦在圆内交叉时, 它们各部分的产品是相等的 。

  播放段落

  Intersecting Chord Theorem
  ::相交弦定理

  播放段落

  Drag the points on the circumference to reposition the chords and observe how the intersecting chord theorem holds true.
  ::拖动周围的点以重新定位和弦 并观察交错的和弦定理是如何真实的

  播放段落

  Example 4
  ::例4

  播放段落

  For the circle below, find $\begin{align*}BF\end{align*}$ .
  ::以下圆形见BF。

  播放段落

  Based on the result of Example #2, you know that $\begin{align*}EF\end{align*}$ $\begin{align*}\cdot\end{align*}$ $\begin{align*}FD\end{align*}$ $\begin{align*}=\end{align*}$ $\begin{align*}BF\end{align*}$ $\begin{align*}\cdot\end{align*}$ $\begin{align*}FC\end{align*}$ $\begin{align*}=\end{align*}$ $\begin{align*}15 \cdot 6 = BF \cdot 9\end{align*}$ . This means that $\begin{align*}BF=10\end{align*}$ .
  ::根据例2的结果,你知道FEF_FD=BFNFFC=15_6=BFB_9。 这意味着BF=10。

  播放段落

  CK-12 PLIX Interactive
  ::CK-12 PLIX 交互式互动

  Summary

  播放段落 An inscribed angle is an angle formed by two chords in a circle which have a common endpoint. ::刻入角是圆形中两个和弦形成的一个角,圆形中有一个共同的终点。 播放段落 The central angle theorem states that the measure of an inscribed angle is half the measure of its intercepted arc. ::中心角定理表明,一个刻着角的测量量是其截取弧的测量量的一半。 播放段落 The intersecting chords theorem states if two chords intersect inside a circle so that one is divided into segments of length $\begin{align*}a\end{align*}$  and $\begin{align*}b\end{align*}$  and the other into segments of length $\begin{align*}c\end{align*}$  and $\begin{align*}d,\end{align*}$  then $\begin{align*}ab = cd.\end{align*}$   ::相交和弦的定理表示,如果两个和弦在圆内交错,则将一个和弦分为a和b的长度部分,另一个和c和d的长度部分,然后ab=cd的长度部分。

  ---

  播放段落

  Review
  ::审查审查审查审查

  播放段落

  1. How are central angles and inscribed angles related?
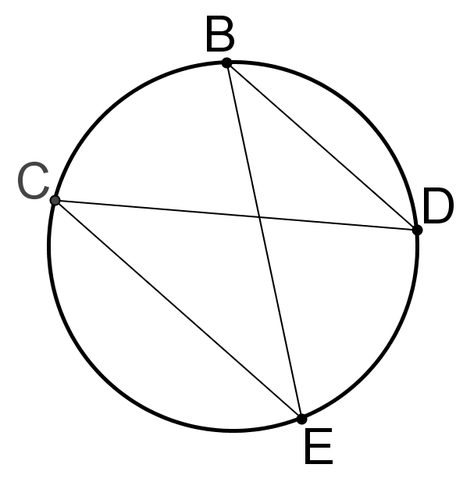
  ::1. 中央角度和刻入角度如何相关?

  播放段落

  In the picture below, $\begin{align*}\overline{BD} \ \| \ \overline{EC}\end{align*}$ . Use the picture below for #2-#6.
  ::在下面的图片中,BD' EC'。用下面的图片来描述#2#6。

  

  播放段落

  2. Find $\begin{align*}m \widehat{BD}\end{align*}$ .
  ::2. 找到 mBD。

  播放段落

  3. Find $\begin{align*}m \angle ABD\end{align*}$ .
  ::3. 找到MáABD。

  播放段落

  4. Find $\begin{align*}m \widehat{EB}\end{align*}$ .
  ::4. 寻找 mEB。

  播放段落

  5. Find $\begin{align*}m \angle ECD\end{align*}$ .
  ::5. 寻找幼儿保育中心。

  播放段落

  6. What type of triangle is $\begin{align*}\triangle ACD\end{align*}$ ?
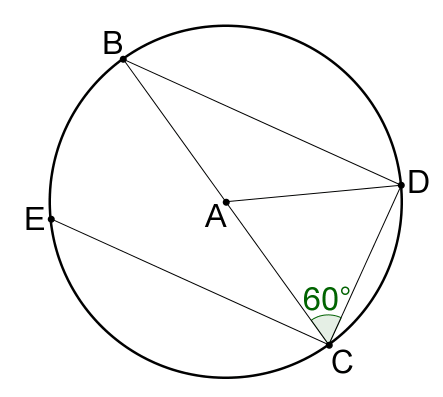
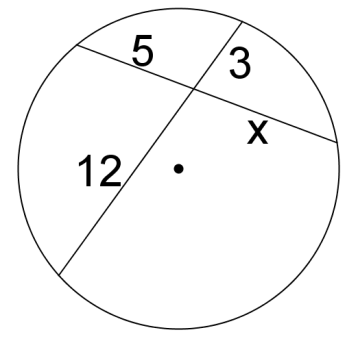
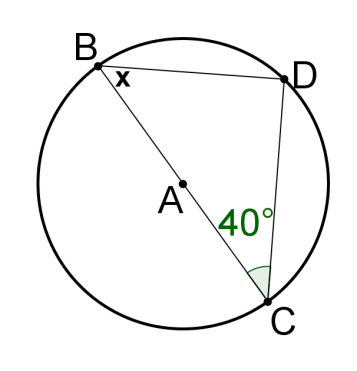
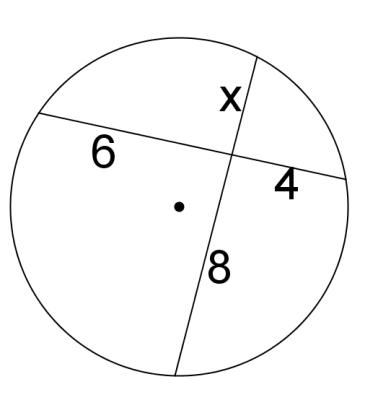
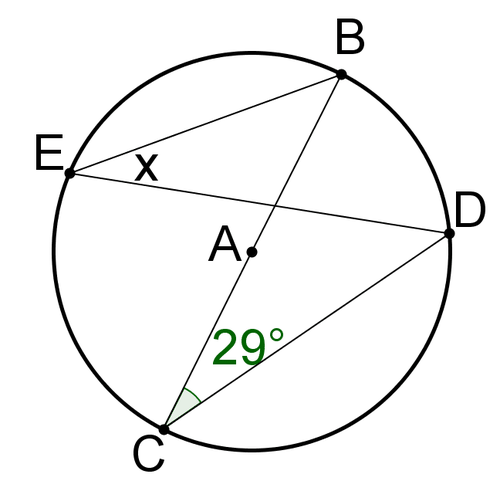
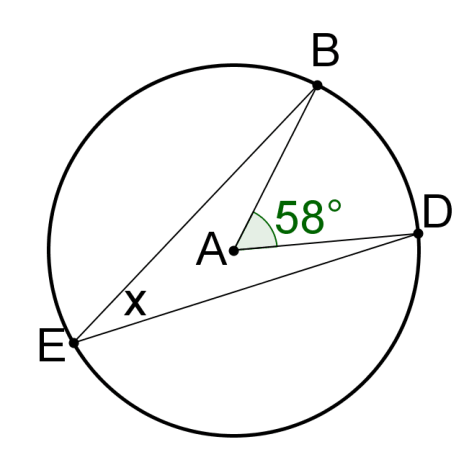
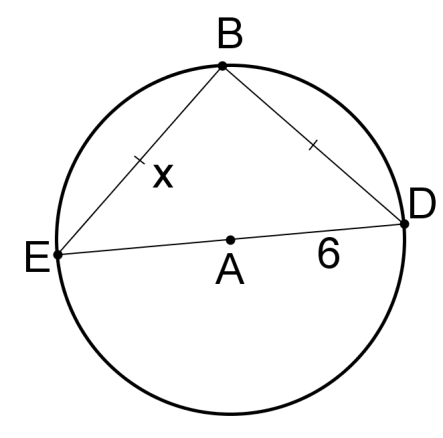
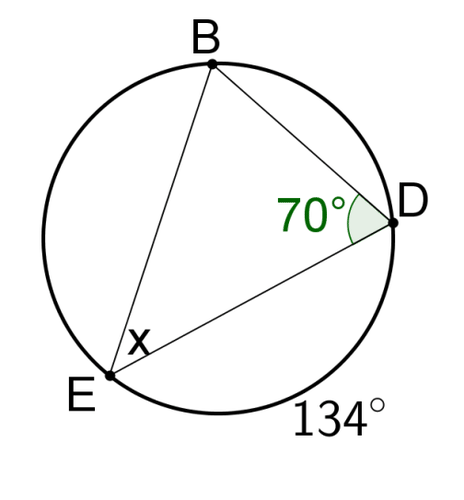
  ::6. 何种三角形是ZACD?

  播放段落

  Solve for $\begin{align*}x\end{align*}$ in each circle. If $\begin{align*}x\end{align*}$ is an angle, find the measure of the angle.
  ::在每个圆圈中为 x 解决。 如果 x 是角度, 请找到角度的量度 。

  7.

  

  8.

  

  9.

  

  播放段落

  10. $\begin{align*}m \widehat{DC} = 95^\circ\end{align*}$
  ::10 mDC95

  

  11.

  

  12.

  

  13.

  

  14.

  

  播放段落

  15. In the picture below, $\begin{align*}\overline{BD}\ || \ \overline{EC}\end{align*}$ . Prove that $\begin{align*}\widehat{BC} \cong \widehat{ED}\end{align*}$ .
  ::15. 如下图所示,BD`EC'证明BC`ED'。

  

  播放段落

  16. Using the diagram below, and knowing that the center of the circle is marked O, how could it be proved that $\begin{align*}m\angle ABC=\frac{1}{2}m\overparen{AC}\end{align*}$ ?
  ::16. 使用下图,并知道圆的中心是O, 如何证明 mABC=12mAC?

  

  17. Compare an inscribed angle and a central angle that intercept the same arc. How do they compare and how do they contrast?

  播放段落

  18. Using the diagram below, explain the relationship between $\begin{align*}\angle ABD\end{align*}$ and $\begin{align*}\angle ACD\end{align*}$ .
  ::18. 使用下图,解释ZABD和QACD之间的关系。

  

  播放段落

  Review (Answers)
  ::审查(答复)

  播放段落

  Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
  ::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键 。