9.7 三个层面的设计问题-interactive

Section outline

• Select section General

  Collapse Expand

  General

  Collapse all Expand all

  • Select activity 新闻通告

    

    新闻通告 Forum
• Select section 三方面设计问题

  Collapse Expand

  三方面设计问题

  播放段落

  When modeling in three dimensions , you are often interested in maximizing or minimizing some aspect of the situation. Perhaps you want to minimize materials used in order to minimize cost. Perhaps you want to maximize the in order to maximize profit.
  ::在三个层面建模时,您往往有兴趣最大限度地或最大限度地减少局势的某些方面,也许您想尽量减少为尽量减少成本而使用的材料,也许您想尽量扩大利润,以便最大限度地增加利润。

  播放段落

  When working with these types of problems, first create your model. Then, test different possibilities or create an equation that shows the relationship between the variable you are looking to maximize or minimize and another variable in the problem.
  ::当处理这些类型的问题时, 请先创建您的模型。 然后, 测试不同的可能性, 或者创建一个公式来显示您想要最大化或最小化的变量与问题中另一个变量之间的关系 。

  播放段落

  To find the maximum or minimum value when you know the equation, you can graph the equation and look for where the graph is at a maximum or a minimum.
  ::要在知道方程式时找到最大值或最小值,您可以绘制方程式图,并查找图形处于最大值或最小值的位置。

  播放段落

  
  Let's take a look at some design problems in three dimensions.
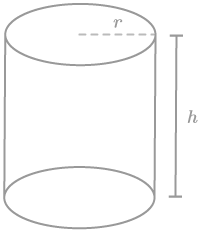
  ::让我们来看看三个维度上的一些设计问题。

  播放段落

  1. A very thin glass container is being designed to hold a candle (it will cover the candle on all sides except the top). The volume of the candle will be 60 cubic inches. If the candle is in the shape of a cylinder , what's an equation that models the amount of glass needed given the radius of the candle?
  ::1. 正在设计一个非常薄的玻璃容器,以保持蜡烛(蜡烛将覆盖除顶部以外的所有侧面的蜡烛),蜡烛的体积将为60立方英寸,如果蜡烛是圆柱形的,那么根据蜡烛的半径计算所需的玻璃量的公式是什么?

  播放段落

  Because the glass is very thin, the amount of glass needed is essentially the of the side and bottom of the cylinder.
  ::由于玻璃非常薄,需要的玻璃数量基本上是圆柱的侧面和底部。

  播放段落
  • The volume of the cylinder is 60 cubic inches, so $\begin{align*}\pi r^2 h=60\end{align*}$ . This means that $\begin{align*}h=\frac{60}{\pi r^2}\end{align*}$ .
    ::圆柱体的体积是60立方英寸, 所以 'r2h=60。 这意味着 h=60立方英寸。
  播放段落
  • The bottom of the cylinder has a surface area of $\begin{align*}\pi r^2\end{align*}$ .
    ::气瓶底部的表面面积为°r2。
  播放段落
  • The lateral face of the cylinder is a rectangle whose dimensions are the height of the cylinder and the of the base. The surface area of the lateral face is $\begin{align*}2 \pi r \left(\frac{60}{\pi r^2}\right)=\frac{120}{r}\end{align*}$ .
    ::圆柱体的横向面是一个矩形,其尺寸是圆柱体和底部的高度。横向面的表面面积是2°r(60°r2)=120r。

  播放段落

  The overall surface area is therefore $\begin{align*}SA=\pi r^2+\frac{120}{r}\end{align*}$ . This is the approximate amount of glass needed for a given radius.
  ::因此,整个表面面积是SAr2+120r,这是给定半径所需的大约玻璃量。

  播放段落

  Using the information from the previous problem , what should the approximate radius and height of the candle be so that the least amount of glass is used for the container?
  ::利用前一个问题的信息,蜡烛的大约半径和高度应该如何才能使容器使用最少的玻璃?

  播放段落

  Use a calculator or graphing program to make a graph of the function $\begin{align*}SA=\pi r^2+\frac{120}{r}\end{align*}$ . Look for where there is a minimum in the graph.
  ::使用计算器或图形程序来绘制 SAr2+120r 函数的图形。 查找图形中最小值的位置 。

  播放段落

  The minimum looks to be a radius of approximately 2.7 inches, producing a surface area of approximately $\begin{align*}67.35 \ \text{in}^2\end{align*}$ . When the radius is 2.7 inches, the height will be $\begin{align*}h=\frac{60}{\pi r^2}=\frac{60}{\pi (2.7)^2} \approx 2.6 \ \text{inches}\end{align*}$ .
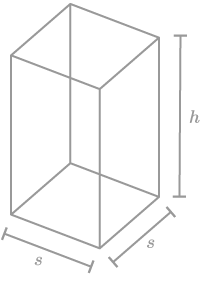
  ::最小半径约为2.7英寸,产生面积约为67.35英寸,当半径为2.7英寸时,高度为h=60°r2=60(2.7)22.6英寸。

  播放段落

  2. A new aquarium is designing a central tank. It will be either a cylinder or a square based prism that is in the center of the building, visible from all floors. If the volume of the tank must be 12,000 cubic feet and the height must be 30 feet, should the tank be a cylinder or a square based prism to minimize the glass needed to build the tank? Note that the top of the tank will be open and the bottom will be concrete.
  ::2. 一个新的水族馆正在设计一个中央水箱,在大楼中心,可以是圆柱体,也可以是广场棱镜,从所有楼层可见,如果罐体体体积必须是12 000立方英尺,高度必须是30英尺,罐体应该是圆柱体,还是广场棱柱,以尽量减少建造罐体所需的玻璃?请注意,罐体顶部是开的,底部是混凝土的。

  

  播放段落

  The glass needed has to do with the surface area of the tank, not including the top or the bottom (which will not be glass).
  ::需要的玻璃与罐体表面有关,不包括顶部或底部(不是玻璃)。

  播放段落

  If we ignore the circular bases the cylinder will have a lateral surface area of  $\begin{align*}2 \pi r h\end{align*}$ . To find the radius, use the fact that the volume must be 12000 cubic feet.
  ::如果我们忽略圆形基座,圆柱体的横向表面面积将为2。要找到半径,请使用体积必须为12,000立方英尺这一事实。

  播放段落

  The surface area of the cylinder is
  ::圆柱体的表面面积是

  播放段落

  If we now ignore the top and bottom bases of the square based prism, then lateral surface area is the sum of the rectangular faces. If the side of the square base is  $\begin{align*}s\end{align*}$ , the lateral surface area is  "> $\begin{align*}4(s)(h)\end{align*}$ . To find the side length, use the fact that the volume must be 12000 cubic feet.
  ::如果我们现在忽略了基于平方棱柱的顶部和底部底部, 那么横向表面积就是矩形面的和和。 如果平方基的侧面是 s, 平面面积是 4 (s) 。 要找到侧面长度, 请使用体积必须为 12 000 立方英尺这一事实 。

  

  播放段落

  The surface area of the prism is
  ::棱晶的表面区域是

  播放段落

  The tank should be a cylinder in order to minimize the amount of glass needed.
  ::罐体应是一个气瓶,以尽量减少所需的玻璃量。

  ---

  播放段落

  In a previous lesson you found that the volume of a cone is found with the formula $\begin{align*}V_{cone}=\frac{\pi{r}^{2}h}{3}\end{align*}$ where $\begin{align*}h\end{align*}$  is the height of the cone and $\begin{align*}r\end{align*}$  is the radius of its circular face. To find the surface area of a cone we need to see that the curved face can be flattened out into a sector .
  ::在上一堂课中,您发现圆锥体的体积与公式Vconer2h3相同,其中圆锥体的高度是h,圆锥体的半径是r。要找到圆锥体的表面区域,我们需要看到曲线面可以被划成一个区块。

  播放段落

  The slant height of the cone $\begin{align*}l\end{align*}$  can be understood as the radius used to find the area of the sector. 
  ::锥形I的倾斜高度可以理解为用于寻找扇形面积的半径。

  播放段落

  $$\begin{align*}\text{Area}_{sector} & = \left(\frac{\theta}{360}\right)\pi {l}^{2}\end{align*}$$
  ::区域面积=( XXX360) l2

  播放段落

  If you don't know the ratio of the angle of the sector to the circle you can instead divide the by the circumference of the circle it belongs to. The arc length of the sector is the same as the circumference of the cone's circular face or $\begin{align*}C_{cone}=2\pi r.\end{align*}$  If the radius of the larger circle is $\begin{align*}l\end{align*}$  then the circumference of that larger circle is  $\begin{align*}C=2\pi l.\end{align*}$ Notice that the ratio $\begin{align*}\frac{2\pi r}{2\pi l}\end{align*}$  simplifies to $\begin{align*}\frac{r}{l}.\end{align*}$ Therefore the area of the sector can also be found with the formula:
  ::如果您不知道扇形角度与圆圈之比, 您就可以用它所属圆圈的环绕来分隔。 扇形的弧长度与锥形圆圆形面或Ccone=2r的环绕相同。 如果大圆的半径为l, 那么大圆的环环为C=2l。 请注意, 2r2l 的比对简化为rl。 因此, 也可以用公式找到扇形的面积 :

  播放段落

  $$\begin{align*}\text{Area}_{sector} & = \left(\frac{r}{l}\right)\pi {l}^{2}\end{align*}$$
  ::扇区=(rl)l2

  播放段落

  This area can be added to the area of the circular face to find the surface area of the complete cone.
  ::这个区域可以添加到圆形区域中,以找到整个圆锥体的表面区域。

  播放段落

  $$\begin{align*}\text{SA}_{cone} & = \left(\tfrac{r}{l}\right)\pi {l}^{2}+\pi {r}^{2}\end{align*}$$
  ::SACONE=(rl)l2r2

  ---

  播放段落

  Examples
  ::实例实例实例实例

  播放段落

  Example 1
  ::例1

  播放段落

  An ice cream cone is made from a thin wafer cookie that is rolled to make the cone shape. The radius of the ice cream cone is 2.5 centimeters and the slant height is 11.5 centimeters. How many square centimeters of wafer cookie are needed to make each ice cream cone?
  ::冰淇淋甜甜圈由薄饼饼干制成,卷成甜甜圈形状。冰淇淋甜甜圈的半径为2.5厘米,斜坡高度为11.5厘米。每个冰淇淋甜甜圈需要多少平方厘米才能制作?

  播放段落

  When unwrapped , the cone is a sector of a circle. The arc length is the circumference of the base of the cone and the radius is the slant height (11.5 cm ).
  ::解包时,锥体是一个圆的区块。弧长度是锥体底部的环形,半径是斜高度(11.5厘米)。

  播放段落

  Use the information from Example #1 for Example #2 and #3.
  ::例2 和 3 使用例1 中的信息。

  播放段落

  Example 2
  ::例2

  播放段落

  To save money, you decide you could either make the cones skinnier or shorter. Which change will cause a bigger change in the surface area: shortening the radius to 2 centimeters or shortening the slant height to 11 centimeters?
  ::为了节省资金,您决定您可以让锥形变浅或变短。 哪种变化会给表面面积带来更大的变化:将半径缩短到2厘米或将倾斜高度缩短到11厘米?

  播放段落

  A bigger change in surface area is caused by shortening the radius.
  ::由于缩短半径,表面积的变化更大。

  播放段落

  Example 3
  ::例3

  播放段落

  Waffle cones have a radius of 4 centimeters and a slant height of 16 centimeters. How much bigger is the surface area of the waffle cone compared to the surface area of the regular ice cream cone?
  ::瓦夫勒锥体的半径为4厘米,斜高度为16厘米。与普通冰淇淋锥的表面积相比,华夫勒锥体的表面积有多大?

  播放段落

  Surface area of the ice cream cone = 90.32  $\begin{align*}\text{cm}^2\end{align*}$ .
  ::冰淇淋锥的表面面积=90.32厘米。

  播放段落

  Difference in the surface area = 201.06 - 90.32 = 110.74  $\begin{align*}\text{cm}^2\end{align*}$ .     
  ::面积差异=201.06-90.32=110.74平方厘米。

  播放段落

  The surface area of the waffle cone is 110.74 square centimeters bigger than a regular ice cream cone.
  ::华夫饼锥体的表面面积是110.74平方厘米,比普通的冰淇淋锥大。

  播放段落

  Example 4
  ::例4

  播放段落

  Come up with a function that outputs the area of wafer cookie needed per cone given the radius and slant height of the cone.
  ::产生一个函数, 输出每个锥体需要的 rafer cookie 区域, 考虑到锥体的半径和倾斜高度 。

  播放段落

  Let $\begin{align*}l=\text{slant height}\end{align*}$ and $\begin{align*}r=\text{radius}\end{align*}$ .
  ::让我们倾斜的高度和 r=radious。

  播放段落

  $\begin{align*}A=\pi l^2 \cdot \frac{2 \pi r}{2 \pi l}=\pi r l\end{align*}$ .
  ::

  播放段落

  CK-12 PLIX Interactive
  ::CK-12 PLIX 交互式互动

  Summary

  播放段落 Use the equation and graph that represents the volume of a shape with variables to solve optimization problems. ::使用方程式和图形来表示带有变量的形状的体积,以解决优化问题。 播放段落 To find the maximum or minimum value when you know the equation, you can graph the equation and look for where the graph is at a maximum or a minimum. ::要在知道方程式时找到最大值或最小值,您可以绘制方程式图,并查找图形处于最大值或最小值的位置。

  ---

  播放段落

  Review
  ::审查审查审查审查

  播放段落

  1. Come up with at least 5 rectangles with a perimeter of 24 inches. Which rectangle has the biggest area?
  ::1. 形成至少5个长方形,周边24英寸,哪个长方形面积最大?

  播放段落

  2. If you did not consider a square in #1, compare the area of a square with perimeter 24 inches to the other rectangles that you came up with. What do you notice?
  ::2. 如果不考虑 #1 中的正方形,将一个正方形面积与周围24英寸之间的区域与您所想出的其他矩形作比较。你注意到什么?

  播放段落

  3. A pentagon has a given perimeter. Make a conjecture about what type of pentagon with this perimeter will have the biggest area.
  ::3. 五边形有一定的周界,推测以这种周界为界的五边形将拥有最大的面积。

  播放段落

  4. A rectangular prism has a given surface area. Make a conjecture about what type of rectangular prism will have the biggest volume.
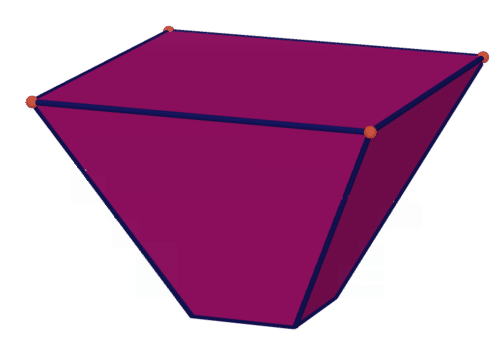
  ::4. 矩形棱柱具有给定的表面面积,对何种类型的矩形棱柱量最大作出推测。

  播放段落

  A new peanut butter company wants to stand out compared with the competition, so decides to design a container that is a truncated pyramid. The top of the container is a square that is 4 inches by 4 inches. The bottom of the container is a square that is 2 inches by 2 inches. The container is 4 inches tall.
  ::一个新的花生酱公司希望与竞争相比更加突出,因此决定设计一个集装箱,它是一个短金字塔。集装箱的顶部是一个方形,4英寸乘4英寸。集装箱的底部是2英寸乘2英寸的方形。集装箱高4英寸。

  

  播放段落

  5. If the pyramid hadn't been truncated, how tall would it have been?
  ::5. 如果金字塔没有被缩短, 它会有多高?

  播放段落

  6. Find the volume of the truncated pyramid.
  ::6. 寻找缺勤金字塔的体积。

  播放段落

  7. Find the surface area of the truncated pyramid.
  ::7. 寻找缺血金字塔的表面面积。

  播放段落

  8. One cubic inch holds 0.45 ounces of peanut butter. How much peanut butter can this container hold?
  ::8. 一立方英寸含有0.45盎司花生酱,该容器能持有多少花生酱?

  播放段落

  9. A typical peanut butter jar is a cylinder with a height of 4 inches and a diameter of 3.9 inches. Compare and contrast this type of jar with the new truncated pyramid container.
  ::9. 典型的花生酱罐是一个圆筒,高度为4英寸,直径为3.9英寸,这种罐子与新的缺油金字塔容器比较和对比。

  播放段落

  An open faced box is being made from a square piece of paper that measures 10 inches by 10 inches. The box will be made by cutting small congruent $\begin{align*}x\end{align*}$ by $\begin{align*}x\end{align*}$ sized squares out of each corner.
  ::正在用一张平方纸制成一个打开的正对面框, 平方纸用10英寸乘10英寸制成。 这个框将用每个角的 x 大小方块切割小相容的 x x 来制成。

  播放段落

  10. What's an equation that relates $\begin{align*}x\end{align*}$ to the volume of the box?
  ::10. 将x与盒子的体积联系起来的方程式是什么?

  播放段落

  11. Graph the equation from #10 and explain what it shows.
  ::11. 从 #10 绘制方程图,并解释其显示的方程。

  播放段落

  12. What size squares should you remove from each corner to maximize the volume?
  ::12. 为使体积最大化,你应该从每个角落移走多少尺寸的方形?

  播放段落

  13. Why does it not make sense to try to minimize the volume of the box?
  ::13. 为什么试图将盒子的体积降到最低是毫无意义的?

  播放段落

  14. The length of the side of the original piece of square paper is $\begin{align*}s\end{align*}$ . Come up with an equation that relates $\begin{align*}s\end{align*}$ , $\begin{align*}x\end{align*}$ , and the volume of the box.
  ::14. 原平面纸的侧面长度为 s. 。 加上一个与s、 x 和盒子的体积相关的方程。

  播放段落

  15. Use your equation to verify that a 15 inch by 15 inch piece of paper with 2 inch by 2 inch square corners removed will produce a box with a volume of $\begin{align*}242 \ in^3\end{align*}$ .
  ::15. 用你的方程式来验证 一张15英寸乘15英寸的纸 2英寸乘2英寸的平方角被移走 会产生一个242英寸的盒子

  播放段落

  16. It's expensive to make aluminum cans. But everyone wants 12 ounces of soda per can. That's about 355 cubic centimeters. Find the minimum amount of surface area for a cylinder with this volume. To do this, write an equation for the surface area as a function of one variable. Use a graphing calculator to find the values for that variable to create a can of the given volume which minimizes surface area. Give the dimensions of the can. Compare this to the actual dimensions of soda cans.
  ::16. 制成铝罐很昂贵。 但每个人都想要每罐12盎司的苏打水。 大约355立方厘米。 找到一个气瓶的最小表面面积。 要做到这一点, 请将表面积的方程式写成一个变量的函数。 使用图形计算器来找到该变量的数值, 以创建一个能将表面面积最小化的罐体。 给定罐体的尺寸。 比较一下苏打罐的实际尺寸 。

  播放段落

  Review (Answers)
  ::审查(答复)

  播放段落

  Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
  ::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键 。