Course: 10.2 圆形等量-interactive

Section outline

Select section General

Collapse Expand
General

Collapse all Expand all
- Select activity 新闻通告
  
  新闻通告 Forum

圆圆平

A circle is one example of a conic section. A circle is the set of all points that are equidistant from a center point. The general equation of a circle is $\begin{aligned} (x - h)^{2} + (y - k)^{2} = r^{2} \end{aligned}$ where $\begin{aligned} (h, k) \end{aligned}$ is the center of the circle and $\begin{aligned} r \end{aligned}$ is the radius of the circle.
::圆是一个二次曲线区域的例子。圆是一个圆形区域。圆形是一个圆形区域。圆形是所有点的一组点,这些点从一个中心点相等。圆形的一般方程式是(x-h)2+(y-k)2=r2,其中(h,k)是圆形的中心,r是圆的半径。

You can derive the equation of a circle with the help of .
::您可以在 . 的帮助下得出圆形的方程。

Deriving the Equation of a Circle
::计算圆形的等量

Consider a circle with center $\begin{aligned} O (0, 0) \end{aligned}$ and $\begin{aligned} r (> 0) \end{aligned}$ be its radius. Let $\begin{aligned} P (x, y) \end{aligned}$ be a point in the plane, then $\begin{aligned} P \end{aligned}$ lies on the circle if $\begin{aligned} | O P | = r \end{aligned}$ . Label the three sides of the right triangle below in terms of $\begin{aligned} x \end{aligned}$ , $\begin{aligned} y \end{aligned}$ and $\begin{aligned} r \end{aligned}$ . Then, use the Pythagorean Theorem to write an equation that shows the relationship between the three sides.
::将一个以 O( 0, 0) 和 r( > 0) 为中心的圆圈视为半径。让 P( x, y) 成为平面的一个点, 如果 \\ OP\ r. Label 位于右三角下方的三边, 即 x, y 和 r 。然后, 使用 Pythagorean 理论来写一个方程式, 显示三边之间的关系。

$\begin{aligned} {O Q}^{2} + {P Q}^{2} & = {O P}^{2} \\ x^{2} + y^{2} & = r^{2} \end{aligned}$
::O2+PQ2=OP2x2+y2=r2

Now, let's prove that all the points on the circle satisfy the equation $\begin{aligned} x^{2} + y^{2} = r^{2} \end{aligned}$ .
::现在,让我们证明圆圈上的所有点都符合公式 x2+y2=r2。

Drag the orange dots on the circle. Notice that when you move the point $\begin{aligned} (x, y) \end{aligned}$ , the lengths of the sides of the triangle will still be $\begin{aligned} x \end{aligned}$ , $\begin{aligned} y \end{aligned}$ and $\begin{aligned} r \end{aligned}$ , so $\begin{aligned} x^{2} + y^{2} = r^{2} \end{aligned}$ will still be true.
::拖曳圆上的橙色点。请注意, 当您移动点( x, y) 时, 三角形两边的长度仍为 x, y 和 r , 所以 x2+y2=r2 将仍然是真实的。

In fact, the set of points that make up the circle is exactly the set of points that satisfy the equation $\begin{aligned} x^{2} + y^{2} = r^{2} \end{aligned}$ . This is why the general equation of a circle centered at the origin is $\begin{aligned} x^{2} + y^{2} = r^{2} \end{aligned}$ , where $\begin{aligned} r \end{aligned}$ is the radius of the circle.
::事实上,构成圆圈的一组点就是符合公式x2+y2=r2的一组点,这就是为什么以原圆为中心的一个圆圈的一般方程是 x2+y2=r2, 其中r是圆圈的半径。

Assume that $\begin{aligned} (x, y) \end{aligned}$ are the coordinates of a point on the circle shown. The center is $\begin{aligned} (h, k) \end{aligned}$ and the radius is $\begin{aligned} r \end{aligned}$ .
::假设 (x,y) 是所显示圆圆上一个点的坐标。中心是 (h, k) , 半径是 r 。

The three sides of the triangle have lengths $\begin{aligned} x - h \end{aligned}$ , $\begin{aligned} y - k \end{aligned}$ and $\begin{aligned} r \end{aligned}$ .
::三角形的三边有x-h、y-k和r的长度。

The relationship between the sides of the triangle is shown with the Pythagorean Theorem:
::三角形两侧的关系与毕达哥伦神话显示如下:

$\begin{aligned} (x - h)^{2} + (y - k)^{2} = r^{2} \end{aligned}$
:x-h)2+(y-k)2=r2

Points on the other side of the circle produce triangles with slightly different side lengths:
::圆角另一侧的点产生三角形,侧长略有不同:

Circle centered at (h,k) with radius r, illustrating Pythagorean Theorem in quadrants.

However, the relationship between the three sides of this triangle is the same, as shown below:
::然而,如下文所示,三角形三侧之间的关系是相同的:

$\begin{aligned} (h - x)^{2} + (k - y)^{2} & = r^{2} \\ ((- 1) (x - h))^{2} + ((- 1) (y - k))^{2} & = r^{2} \\ (- 1)^{2} (x - h)^{2} + (- 1)^{2} (y - k)^{2} & = r^{2} \\ (x - h)^{2} + (y - k)^{2} & = r^{2} \end{aligned}$
:h-x)2+(k-y)2=r2((-1)(x-h))2+((-1)(y-k))2+((-1(-1)(y-k))2=r2(-1)(2)(x-h)2+(-1)(-1)(y-k)2+(-1)(2)2=r2(x-h)2=r2(x-h)2+(y-k)2+(y-k)2=r2

The set of points that satisfy the equation $\begin{aligned} (x - h)^{2} + (y - k)^{2} = r^{2} \end{aligned}$ are the set of points that make up the circle.
::符合等式(x-h)2+(y-k)2=r2的一组点是构成圆形的一组点。

A certain circle can be represented by $\begin{aligned} x^{2} + y^{2} - 6 x + 8 y - 11 = 0 \end{aligned}$ . What is the center and radius of this circle?
::某个圆可以用 x2+y2 - 6x+8y - 11=0 表示。这个圆的中间和半径是什么 ?

The center and radius of this circle is .
::此圆的中间和半径是。

Circle
::圆圆

Click the small blue arrow next to the image below and drag the orange points to vary the radius and move the center of the circle in the coordinate plane and observe the equation of the circle change accordingly.
::单击下方图像旁边的小蓝箭头,拖动橙色点以改变半径,移动坐标平面圆圆的中心,并相应观察圆形的方程。

Examples
::实例实例实例实例

Example 1
::例1

What type of graph is produced by the equation $\begin{aligned} x^{2} - 2 x + y^{2} - 4 y + 1 = 0 \end{aligned}$ ? How can you turn this equation into graphing form in order to graph it?
::方程式 x2 - 2x+y2 - 4y+1=0 生成何种类型的图形? 您如何将此方程式转换成图形形式以图解 ?

The equation $\begin{aligned} x^{2} - 2 x + y^{2} - 4 y + 1 = 0 \end{aligned}$ is the equation for a circle. You can tell it is a circle because there is both an $\begin{aligned} x^{2} \end{aligned}$ term and a $\begin{aligned} y^{2} \end{aligned}$ term, and the coefficients of each are the same. To turn this equation into the form $\begin{aligned} (x - h)^{2} + (y - k)^{2} = r^{2} \end{aligned}$ , you must complete the square twice. Remember that when completing the square, you are trying to figure out what number to add to make a perfect square trinomial. In order to maintain the equality of the equation, you must add the same numbers to both sides of the equation.
::x2 - 2x+y2 - 4y+1=0 是圆形的方程式。您可以通过 x2 和 y2 和 y2 和 y2 和 =0 来分辨一个圆形。要将方程式转换成窗体( x- h) 2+(y- k) 2 =r2, 您必须两次完成方形。记住, 当完成方形时, 您正在试图找出要添加什么数字来制作一个完美的平方三角形。为了保持公式的平等, 您必须在方形的两侧添加相同数字。

$\begin{aligned} x^{2} - 2 x + \underline{} + y^{2} - 4 y + \underline{} = - 1 \\ x^{2} - 2 x + \underline{1} + y^{2} - 4 y + \underline{4} = - 1 \underline{+ 1 + 4} \\ x^{2} - 2 x + 1 + y^{2} - 4 y + 4 = 4 \\ (x - 1)^{2} + (y - 2)^{2} = 4 \end{aligned}$
::x2 - 2x- 2x_ y2- 4y_ 4x+1x2+1+4_ x2-2x+1+4_ x2-2x+1+y2- 4y+4=4(x-1)2+(y-2)2=4

Example 2
::例2

What is the equation of a circle centered at $\begin{aligned} (- 4, 5) \end{aligned}$ with a radius of $\begin{aligned} \sqrt{2} \end{aligned}$ ?
::以(- 4, 5) 为中心、半径为 2 的圆形的方程式是多少 ?

The center of the circle is $\begin{aligned} (- 4, 5) \end{aligned}$ and its radius is $\begin{aligned} \sqrt{2} \end{aligned}$ units.
::圆的中心是 (- 4, 5) , 半径为 2 个单位。

$\begin{aligned} h = - 4 \end{aligned}$ , $\begin{aligned} k = 5 \end{aligned}$ and $\begin{aligned} r = \sqrt{2} \end{aligned}$ .
::h4, k=5 和 r=2。

The equation of the circle is
::圆的方形是

$\begin{aligned} (x - h)^{2} + (y - k)^{2} & = r^{2} \\ (x - (- 4))^{2} + (y - 5)^{2} & = (\sqrt{2})^{2} \\ (x + 4)^{2} + (y - 5)^{2} & = 2 \end{aligned}$
:x-h)2+(y-k)2=r2(x-(-4))2+(y-5)2+(y-5)2=(2)2(x+4)2+(y-5)2=2

Notice that the signs of the 4 and the 5 in the equation are opposite from the signs of the 4 and the 5 in the center point.
::注意方程中4和5的标志与中点中4和5的标志相反

Example 3
::例3

What are the center and radius of the circle described by the equation:
::方程式所描述的圆圆的中心与半径是多少 :

$\begin{aligned} x^{2} - 4 x + y^{2} + 10 y + 13 = 0 \end{aligned}$ ?
::x2-4x+y2+10y+13=0?

Complete the square to rewrite the equation in graphing form:
::完成正方形以图示形式重写方形 :

$\begin{aligned} x^{2} - 4 x + \underline{4} + y^{2} + 10 y + \underline{25} & = - 13 \underline{+ 4 + 25} \\ (x - 2)^{2} + (y + 5)^{2} & = 16 \\ (x - 2)^{2} + (y + 5)^{2} & = 4^{2} \end{aligned}$
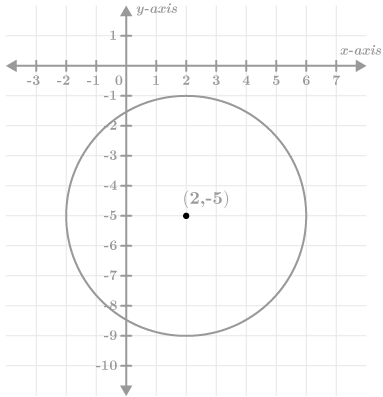
::x2 - 4x+4+42+10y+2513+4+25_(x-2)2+(y+5)2+16(x-2)2+(y+5)2+(y+5)2=42

The center of the circle is $\begin{aligned} (2, - 5) \end{aligned}$ and the radius is 4.
::圆的中心是(2,-5),半径是4。

Example 4
::例4

Graph the circle from Example #3.
::从例3中绘制圆形图。

A graph showing a circle centered at (2, -5) on a coordinate plane.

CK-12 PLIX: Circles in the Coordinate Plane
::CK-12 PLIX: 坐标平面中的圆圈

Summary

A circle is a set of all points that are the same distance away from a specific point, called the center. The standard form of a circle with center $\begin{aligned} (h, k) \end{aligned}$ and radius, $\begin{aligned} r \end{aligned}$ :
$\begin{aligned} (x - h)^{2} + (y - k)^{2} = r^{2} \end{aligned}$
::a 圆是一组所有点的集合点,这些点与特定点的距离相同,称为中点。圆的标准形式,以(h,k)和半径为中心,rx-h)2+(y-k)2=r2。

When finding the standard form of a circle complete the square twice (figure out what number to add to make a perfect square trinomial).
::当找到一个圆的标准形式时, 圆将完成方形的两次( 算出要加多少数来做一个完美的正方形三角形 ) 。

Review
::审查审查审查审查

Graph the following circles:
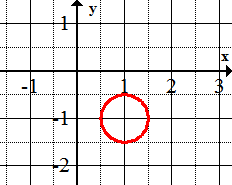
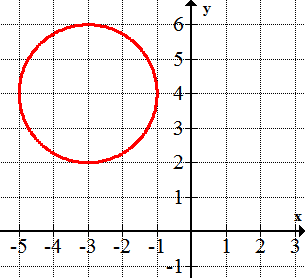
::绘制以下圆形图:

1. $\begin{aligned} (x + 2)^{2} + (y - 5)^{2} = 1 \end{aligned}$
::1. (x+2)2+(y-5)2=1

2. $\begin{aligned} (x - 1)^{2} + (y + 1)^{2} = 3 \end{aligned}$
::2. (x-1)2+(y+1)2=3

3. $\begin{aligned} (y + 4)^{2} + (x - 3)^{2} = \frac{1}{4} \end{aligned}$
::3. (y+4)2+(x-3)2=14

4. $\begin{aligned} x^{2} + (y - 6)^{2} = 8 \end{aligned}$
::4. x2+(y-6)2=8

5. $\begin{aligned} (x - 2)^{2} + y^{2} = 25 \end{aligned}$
::5. (x-2)2+y2=25

Find the center and radius of the circle described by each equation.
::查找每个方程式所描述的圆圆的中心和半径。

6. $\begin{aligned} x^{2} + 4 x + y^{2} + 4 y + 7 = 0 \end{aligned}$
::6. x2+4x+y2+4y+7=0

7. $\begin{aligned} x^{2} - 2 x + y^{2} + 12 y + 32 = 0 \end{aligned}$
::7. x2-2x+y2+12y+32=0

8. $\begin{aligned} x^{2} - 2 x + y^{2} - 2 y = 0 \end{aligned}$
::8. x2-2x+y2-2yy=0

9. $\begin{aligned} x^{2} + 8 x + y^{2} + 9 = 0 \end{aligned}$
::9. x2+8x+y2+9=0

10. $\begin{aligned} x^{2} + 2 x + y^{2} - 6 y + 1 = 0 \end{aligned}$
::10. x2+2x+y2-6y+1=0

11. Explain why a circle with radius $\begin{aligned} r \end{aligned}$ that is centered at the origin will have the equation $\begin{aligned} x^{2} + y^{2} = r^{2} \end{aligned}$ .
::11. 解释为什么以原点为中心、以 r 圆为半径的圆将具有 x2+y2=r2 方程式。

12. Use the Pythagorean Theorem to help explain why a circle with a center in the second quadrant with radius $\begin{aligned} r \end{aligned}$ and center $\begin{aligned} (h, k) \end{aligned}$ will have the equation $\begin{aligned} (x - h)^{2} + (y - k)^{2} = r^{2} \end{aligned}$ . Note that in the second quadrant the value for $\begin{aligned} h \end{aligned}$ will be negative and the value for $\begin{aligned} k \end{aligned}$ will be positive.
::12. 使用 Pythagorean Theorem 帮助解释为什么在第二个象限内有一个中心,以半径(h,k)和中(h,k)为圆心的圆将具有等式(x-h)2+(y-k)2=r2. 注意在第二个象限内,工龄为负值,叉子为正值。

13. Use the Pythagorean Theorem to help explain why a circle with a center in the third quadrant with radius $\begin{aligned} r \end{aligned}$ and center $\begin{aligned} (h, k) \end{aligned}$ will have the equation $\begin{aligned} (x - h)^{2} + (y - k)^{2} = r^{2} \end{aligned}$ . Note that in the third quadrant the value for $\begin{aligned} h \end{aligned}$ will be negative and the value for $\begin{aligned} k \end{aligned}$ will be negative.
::13. 使用 Pythagorean Theorem 帮助解释为什么在第三个象限内有一个中心圆,其半径(h,k)和中(h,k)将具有方程(x-h)2+(y-k)2=r2。请注意,在第三个象限内, h值为负值,叉值为负值。

14. Write the equation of the following circle:
::14. 写下以下圆形的方程:

15. Write the equation of the following circle:
::15. 写下以下圆形的方程:

16. A rectangle is inscribed in a circle of diameter 12. Determine the function for the area of the rectangle in terms of x . Determine the value of x such that the area of the rectangle is maximized. Justify your answer.
::16. 矩形以直径的圆形刻入一个矩形。12. 以 x 表示矩形区域的函数。确定 x 的值,以使矩形的面积最大化。请说明答案的理由。

17. Consider a series of circles such that h = k. If the radius is 2 and k is any real number, give a description that satisfies all of the members of the series.
::17. 如果半径为2和K是任何实际数字,请说明符合系列所有成员的要求。

18. Given the points $\begin{aligned} A (3, 4), B (- 3, - 4), and C (x, y), \end{aligned}$ on a circle, what is the relationship between points $\begin{aligned} A, B, and C, if \bar{C A} ⊥ \bar{C B} ? \end{aligned}$ Explain your answer.
::18. 鉴于A(3,4)、B(3,4)和C(x,y)点在圆圈上,如果CA {CB}==CB,那么A、B和C(x,y)点之间的关系是什么?请解释你的答复。

Review (Answers)
::审查(答复)

Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键。

Section outline

General

圆圆平

Deriving the Equation of a Circle ::计算圆形的等量

Circle ::圆圆

Examples ::实例实例实例实例

Example 1 ::例1

Example 2 ::例2

Example 3 ::例3

Example 4 ::例4

CK-12 PLIX: Circles in the Coordinate Plane ::CK-12 PLIX: 坐标平面中的圆圈

Review ::审查审查审查审查

Review (Answers) ::审查(答复)