2.1 职能-interactive

章节大纲

• 选择节常规

  折叠 展开

  常规

  全部折叠 展开全部

  • 选择活动新闻通告

    

    新闻通告 讨论区
• 选择节职能职能职能职能职能职能职能职能职能职能职能职能职能职能职能

  折叠 展开

  职能职能职能职能职能职能职能职能职能职能职能职能职能职能职能

  播放段落

  Learning Objectives
  ::学习目标

  播放段落
  • Understand that a function is a rule that assigns to each input exactly one output.
    ::理解一个函数是一个规则,为每个输入指定一个精确输出。
  播放段落
  • C alculate output values given an input value of a function, given a table, diagram, or equation .
    ::计算输出值,给定函数的输入值,给定表格、图表或方程式。
  播放段落
  • Identify whether a relation is a function or not, and use the vertical line test .
    ::确定关系是否是一个函数,并使用垂直线测试。
  播放段落
  • Use the vertical line test to check if the graph of a relation is a function.
    ::使用垂直线测试来检查关系图是否是一个函数。
  播放段落
  • Understand what continuous and  discrete functions are .
    ::了解什么是连续和独立的功能。
  播放段落
  • Understand what domain and range are in terms of a function.
    ::了解函数的域和范围。
  播放段落
  • Identify the domain and range of a function.
    ::确定函数的域和范围。

  ---

  播放段落

  Introduction: Functions
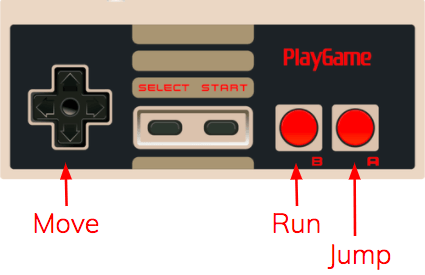
  ::导言:职能

  

  播放段落

  In a video game,  a controller inputs information that the game translates to actions on the part of the character  being controlled.  Using  math terminology,  you'd say that the actions of the character are a function of the buttons pressed on the controller. For example, a video game controller might have the following button designations:
  ::在视频游戏中,一个控制器输入信息,该游戏转换为被控制字符的动作。使用数学术语,你会说该字符的动作是按在控制器上的按钮的函数。例如,一个视频游戏控制器可能具有以下按钮名称:

  

  播放段落

  Discussion Question : In the example above, the " A " button will result in the character jumping. Is it possible more than one button to be pressed at once? What actions could this have on the character in this example?
  ::讨论问题:在以上例子中,“ A” 按钮会导致字符跳跃。 是否可以同时按下不止一个按钮? 这对示例中的字符有什么作用 ?

  ---

  播放段落

  Activity 1: What is a Function?
  ::活动1:什么是功能?

  播放段落

  The idea of a function is simple: put something into a function (the input), a process is performed (the rule), and get a modified version of the input (the output). Functions may seem like an abstract math topic. However, not only do they exist in math, but they exist in every programming language.
  ::函数的概念很简单: 将某个东西放入函数( 输入) , 执行一个进程( 规则) , 并获得一个修改版本的输入( 输出) 。 函数可能看起来像一个抽象的数学专题。 但是, 它们不仅存在于数学中, 而且存在于每种编程语言中 。

  播放段落

  Example
  ::示例示例示例示例

  

  播放段落

  Carlos is an engineer that is designing a program to control the temperature in an aquarium tank. The temperature in the tank should be 78°F and never vary by more than 2°F. Can Carlos use a function to create an alert if the temperature varies by more than 2°F? What would this function look like?
  ::Carlos是一位设计一个程序来控制水族箱温度的工程师。 罐体温度应该为78°F, 变化不得超过2°F。 如果温度变化超过2°F, Carlos能否使用一个函数来生成警报? 这个函数是什么样子的?

  播放段落

  Carlos wants the program to take the temperature of the tank and find out how far it is from 78°F. The temperature is the input, and the distance from 78°F is the output. While there are many ways that this can be accomplished in programming, absolute value functions are commonly used to find the distance from a value. The function below will find the distance of the input temperature from 78°F.
  ::Carlos想让程序从罐体温度中测出离78°F有多远。 温度是输入, 距离78°F是输出。 虽然在编程中有许多方法可以实现这一点, 但绝对值函数通常用来寻找与值的距离。 下面的函数会找到输入温度与78°F的距离 。

  In mathematics	In Python	In JavaScript
  $\begin{align*}f(x)=|x-78|\end{align*}$	播放段落 def f(x): ::def f( x) : 播放段落      return abs(x-78) ::返回 abs(x-78)	播放段落 function f(x)  { ::函数 f(x) { 播放段落      return Math.abs(x-78); ::返回 Math.abs(x-78); }

  播放段落

  A function is defined as the relationship between an input set and an output set where each input has only one output. In some functions, the output values can be predicted based on a mathematical relationship.  For example, the relationship between the temperature and its distance from 78°F, displayed above, defines the output values. If a temperature of 76.6°F is input, the output will always be 1.4°F. T he graph below represents the relationship between the input temperature and the output distance from 78°F.
  ::函数的定义是输入集和输出集之间的关系,其中每个输入只有一个输出。在有些函数中,输出值可以基于数学关系预测。例如,上面显示的温度和距离78°F之间的关系定义输出值。如果输入的温度为76.6°F,则输出始终为1.4°F。下图显示输入温度和78°F输出距离之间的关系。

  

  播放段落

  F unctions aren't always defined by a predetermined mathematical rule. In  some cases, data is used to find the function that best models the relationship. These functions occur when the data has an element of randomness determined by human behavior or environmental factors, or something else . The function below represents the velocity of a  cheetah over time. The relationship between velocity and time is formed by the decisions of the cheetah rather than a mathematical rule.
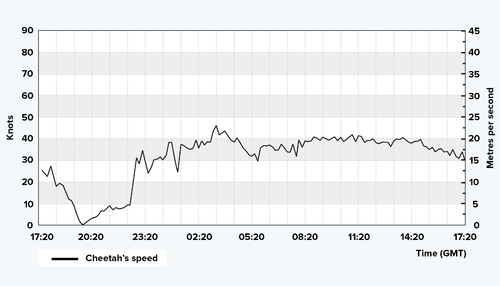
  ::函数并不总是由预设的数学规则来定义。 在某些情况下, 数据被用来查找最能模拟关系模式的函数。 这些函数发生于数据具有随机性元素时, 随机性元素是由人类行为或环境因素或其他因素决定的。 下面的函数代表着猎豹随时间推移的速度。 速度和时间之间的关系是由猎豹的决定而不是数学规则所决定的。

  

  播放段落

  As you  progress through Algebra 2, you will learn how to apply mathematical rules to represent tendencies and patterns occurring in functions that seem to have no mathematical relationship on the surface.
  ::随着代数2的进展,你会学会如何应用数学规则 来代表在表面似乎没有数学关系的函数中出现的趋势和模式。

  ---

  播放段落

  Extension: Identifying Functions
  ::扩展:确定职能

  ---

  播放段落

  Activity 2: Discrete and Continuous Functions
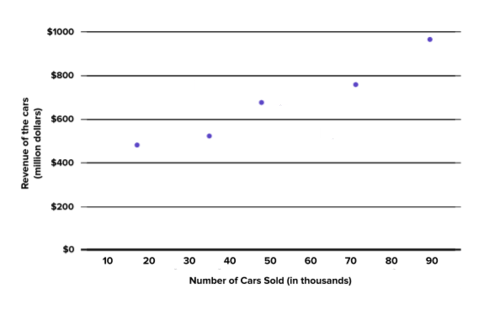
  ::活动2:分立和连续函数

  播放段落

  Functions can also be used to model data that is discrete or continuous. A discrete function is a function with distinct input values. An example of a discrete function would be the revenue from selling $\begin{align*}x\end{align*}$  cars. You would not be able to find  $\begin{align*}f(0.1)\end{align*}$  because you can’t sell 0.1 cars.
  ::函数也可以用来模拟离散或连续的数据。 离散函数是一个具有不同输入值的函数。 离散函数的一个实例是出售 x 汽车的收入。 您找不到 f( 0.1) , 因为无法出售 0.1 辆汽车 。

  播放段落

  Example
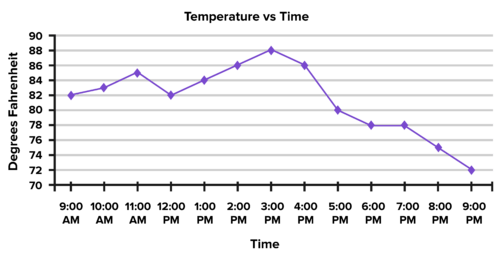
  ::示例示例示例示例

  

  播放段落

  A continuous function is a function with no restrictions on input values over a finite or infinite interval and no breaks or areas where the output values are not connected. The temperature throughout a day is an example of a continuous function because you can find the temperature at any time over the 24-hour period.
  ::连续函数是一个函数,对一定或无限间隔的输入值没有任何限制,没有断裂或输出值没有连接的区域。一天的温度是连续函数的一个实例,因为24小时的任何时候都能找到温度。

  播放段落

  Example
  ::示例示例示例示例

  

  播放段落

  Discussion Question : For the function $\begin{align*}f(x)=|x−78|,\end{align*}$   are there any output values which would be impossible to get from this function? Discuss with others in person or online. How can you most efficiently describe any limitations that the output has? Why is your description preferable to someone else's ?
  ::讨论问题:对于 f(x) x- 78 {} 函数,是否有无法从此函数获得的产出值? 与其他人面对面讨论或在线讨论。 您如何最有效地描述输出的局限性? 为什么您的描述比别人的描述更可取?

  ---

  播放段落

  Activity 3: Domain & Range
  ::活动3: 域和范围

  播放段落

  The inputs and outputs of a function are referred to as the domain and range, respectively.  As seen in the previous activity, a function can be a finite set of individual values or an infinite set of values. The following examples illustrate how to write a domain or range depending on whether the graph is discrete or continuous.
  ::函数的输入和输出分别称为域和范围。如前一活动所示,函数可以是一组有限的单个值,也可以是一组无限的值。以下示例说明如何根据图形是离散的还是连续的来写入一个域或范围。

  播放段落

  Example
  ::示例示例示例示例

  播放段落

  The points below represent the height of a plant, in cm, $\begin{align*}x\end{align*}$  weeks after  it was planted. The number of weeks is the input and is written in the x-position of the coordinate. The height of the plant is the output and is written in the $\begin{align*}y\end{align*}$  position of the coordinate. What is the domain and range of the following function?
  ::以下各点代表植物的高度, 以厘米为单位, 种植后 x 周。 周数是输入数, 以坐标的 x 位置写成 。 工厂的高度是输出数, 以坐标的 y 位置写成 。 以下函数的域和范围是什么 ?

  $\begin{align*}\left\{(0, 0), (1, 0.2), (2, 0.6), (3, 1.5), (4, 2.8), (5, 3.8)\right\}\end{align*}$

  播放段落

  Since this function is a finite set of individual points, it is a discrete function. The domain of a discrete function is a set of distinct input values which, as in this case, are commonly the $\begin{align*}x\end{align*}$   values. Therefore the domain is  $\begin{align*}\left\{0,1,2,3,4,5\right\}.\end{align*}$   Since this is a set of consecutive natural numbers, this can also be written in set builder notation as $\begin{align*}\left\{x | x∈ℕ, 0 ≤ x ≤ 5\right\}.\end{align*}$  Re call that ℕ means the set of natural numbers. The range is the set of all $\begin{align*}y\end{align*}$  (output) values  $\begin{align*}\left\{0, 0.2, 0.6, 1.5, 2.8, 3.8\right\}.\end{align*}$  Unlike with the domain, there is no easy way to write this using set-builder notation . As a result, this is the best approach to writing the range.
  ::由于此函数是单个点的有限数组, 它是一个离散函数。 离散函数的域是一组不同的输入值, 与本案相同, 这些输入值通常是 x 值。 因此, 域是 {0, 1, 2, 34, 5} 。 由于这是一组连续的自然数字, 这也可以写成为 {x*xN, 0x=5} 。 回顾 N 是指一组自然数字。 范围是全部 y( 输出) 值的集合 {0, 0.2, 0.6, 1.5, 2. 8, 3.8} 。 与域不同, 使用 sec- builder 的标记来写入这个域是不容易的。 因此, 这是写范围的最佳方法 。

  播放段落

  Answer:  Domain =  $\begin{align*}\left\{0,1,2,3,4,5\right\}\end{align*}$   or  $\begin{align*}\left\{x | x∈ℕ, 0 ≤ x ≤ 5\right\}\end{align*}$  and Range =  $\begin{align*}\left\{0, 0.2, 0.6, 1.5, 2.8, 3.8\right\}\end{align*}$
  ::答复:域 = {0,1,2,3,4,5} 或{xxN,0x5} 和范围 = {0.0.2.00.6,1.5.2.8,3.8}

  播放段落

  Use the interactive below to practice finding the domain and range of a discrete function.
  ::使用下面的交互功能来实际查找一个离散函数的域和范围。

  播放段落

  Example
  ::示例示例示例示例

  播放段落

  In the introduction, a function was written to find the distance of a temperature from 78°F. What is the domain and range of that function $\begin{align*}f(x)=|x - 78|?\end{align*}$
  ::在导言中,写了一个函数以查找温度与78°F的距离。 该函数f(x)x-78的域和范围是什么?

  播放段落

  U se the graph of the function to help find the domain and range.
  ::使用函数的图形帮助查找域和范围。

  

  播放段落

  The graph of the function is solid with no dashes or breaks because the data is continuous. The domain and range of a continuous function are commonly written as inequalities or using interval notation. Since any temperature can be entered into the function, the domain is the set of all real numbers . The set of all real numbers can be written as the compound inequality  $\begin{align*}\text{-}∞ < x < ∞\end{align*}$  or in interval notation as  $\begin{align*}(\text{-}∞,∞).\end{align*}$  The set of all real numbers can also be written in set builder notation as $\begin{align*}\{x|x∈ℝ\}\end{align*}$  or using the shorthand ℝ. The function , however,  will not produce  just any value as an output. There is no way to get a negative number from the function, as illustrated in the graph. Therefore, the range of the function will be the set of numbers greater than or equal to zero . This set can be written as the compound inequality  $\begin{align*}0 < y < ∞\end{align*}$   or in interval notation as  $\begin{align*}[0,∞).\end{align*}$  The compound inequality  $\begin{align*}0 < y < \infty \end{align*}$  is often written as  $\begin{align*}0 < y \text{ or } y > 0.\end{align*}$
  ::函数的图形是固态的,没有破折号,因为数据是连续的。连续函数的域和范围通常写成为不平等或使用间距符号。由于可以输入任何温度,因此此域是所有实际数字的一组。所有实际数字的一组可以写成复合不平等 -x 或以(-,) 的间距表示(-,) 。所有实际数字的一组也可以写成以 {xx{R} 或以短手R 的形式表示。但是,该函数不会以输出的形式产生任何值。因此,无法从函数中获得负数,如图表所示。因此,该函数的范围将是大于或等于零的数组。该组可以写成复合不平等 0<y 或以间距表示 [0,] 。复合不平等 0<y 通常写成为 0<y或y>0。

  播放段落

  Answer:  Domain =  $\begin{align*}−∞ < x < ∞\end{align*}$   or  $\begin{align*}(−∞,∞)\end{align*}$  or ℝ and Range =  $\begin{align*}y > 0\end{align*}$   or  $\begin{align*} [0,∞) \end{align*}$
  ::答复: 域 = x 或 (,) 或 R 和 范围 = y>0 或 [0,]

  播放段落

  Use the interactive below to practice finding the domain and range of a continuous function.
  ::使用下面的交互功能来实际查找连续函数的域和范围。

  ---

  播放段落

  Activity 4 : Domain and Range in Context
  ::活动4: 活动4: 所涉领域和范围

  播放段落

  In previous examples, the domain and range were determined by either a given set of points or a mathematical relationship. However, when using functions in the real world, the domain and range of a function may contain values that do not make sense in  the context of the situation.
  ::在以前的例子中,域和范围是由特定一组点或数学关系决定的,但是,在使用现实世界的函数时,函数的域和范围可能包含在当时情况下没有意义的数值。

  播放段落

  Example
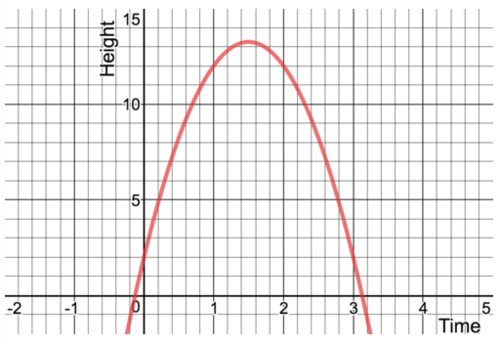
  ::示例示例示例示例

  播放段落

  At a hockey game, small foam pucks are launched into the stands, starting from the height of 2 meters above the ice surface. The model for the vertical motion of the puck can be approximated using the function  $\begin{align*}h(t)=−5t^2+15t+2,\end{align*}$  where $\begin{align*}t\end{align*}$  is the time in seconds and $\begin{align*}h\end{align*}$  is the height in meters. A graphical representation of the function can be seen below:
  ::在曲棍球比赛中,小型泡沫球棒从冰层上方2米高处开始发射到站台。圆球的垂直运动模型可以使用函数 h(t) @%5t2+15t+2来近似,其中 t 是秒中的时间, h 是米中的高度。 函数的图形表达方式如下:

  

  播放段落

  Are there any restrictions on the domain and range?
  ::这一领域和范围是否有任何限制?

  播放段落

  The  graph of the function shows values in all four quadrants . Why do you think this is not a reasonable interpretation of the graph for this problem?
  ::函数的图形显示所有四个四等量的数值。为什么你认为这个图表不能合理地解释这个问题?

  播放段落

  Use this interactive to explore the situation further.
  ::利用这一互动方式进一步探讨情况。

  ---

  播放段落

  Extension: Functions with Multiple Inputs
  ::扩展名: 有多个输入功能的函数

  播放段落

  In textbooks, functions with multiple inputs are rarely seen. However, in the programming world, this is common. A simple example of this is the area of a rectangle.
  ::在教科书中,很少看到具有多种投入的功能,但在编程世界中,这种情况很常见,这方面的一个简单例子是矩形领域。

  播放段落

  Example
  ::示例示例示例示例

  播放段落

  Write a math function that will find the area of the rectangle below.
  ::写入数学函数, 以找到下面矩形的区域 。

  

  播放段落

  To find the area of a rectangle, multiply the length by the width. However,  there are three variables: $\begin{align*}A\end{align*}$  (area), $\begin{align*}l\end{align*}$  (length), and $\begin{align*}w\end{align*}$  (width). Which variable is the input value, and which is the output value?
  ::要找到矩形区域, 请将长度乘以宽度。 但是, 有三个变量 : A( 区域 ) 、 l( 长度) 和 w( 宽) 。 哪个变量是输入值, 哪个变量是输出值 ?

  播放段落

  Since you want to find the area, this will be the output value. The area is determined using the length and width, so these will be the input values.
  ::既然您想要找到此区域,这就是输出值。此区域是使用长度和宽度确定的,因此这就是输入值。

  

  播放段落

  W rite a function to find the perimeter. How would you graph the function above?  Describe  a situation where more than two inputs would be needed (hint: think in terms of dimensions of an object).
  ::写入函数以查找周边。 您如何绘制上面的函数? 描述需要两个以上输入的情况( 内容: 思考对象的尺寸) 。

  播放段落

  Choose a real-world scenario and write a function with multiple inputs to model it.
  ::选择一个真实世界情景,并写入含有多个输入的函数来建模它。

  ---

  播放段落

  Wrap-Up: Review Questions
  ::总结:审查问题

  播放段落

     Summary
  ::摘要

  播放段落
  • A function is a relation where each input has one and only one output.
    ::函数是每个输入有一个和只有一个输出的关联。
  播放段落
  • The notation for a function is $\begin{align*}f(x).\end{align*}$  
    ::函数的符号为 f(x) 。
  播放段落
  • Use the vertical line test to check if the graph of a line is a function. If the graph of a line has two $\begin{align*}y\end{align*}$  values for one $\begin{align*}x\end{align*}$  value, it is not a function.
    ::使用垂直线测试来检查一行的图形是否是一个函数。如果一行的图形为一个 x 值有两个y值,它不是一个函数。
  播放段落
  • A discrete function is a function with distinct input values.
    ::独立的函数是具有不同输入值的函数。
  播放段落
  • A continuous function is a function with  no restrictions on input values over a finite or infinite interval.
    ::连续函数是一个在一定间隔或无限间隔内不限制输入值的函数。
  播放段落
  • The domain of a function is the set of input values. The range of a function is the set of output values.
    ::函数的域是输入值的一组。函数的范围是输出值的一组。