2.4 图形构造函数-interactive

章节大纲

• 选择节常规

  折叠 展开

  常规

  全部折叠 展开全部

  • 选择活动新闻通告

    

    新闻通告 讨论区
• 选择节图图函数

  折叠 展开

  图图函数

  播放段落

  Learning Objectives
  ::学习目标

  播放段落
  • Graph a nonlinear function by plotting points.
    ::通过绘图点绘制非线性函数图。
  播放段落
  • Understand what the zeros of a function are and how to find them.
    ::了解函数的零和如何找到它们。
  播放段落
  • Find the x - intercepts and y - intercepts of a nonlinear function.
    ::查找非线性函数的 X 界面和 Y 界面。
  播放段落
  • Solve systems of two nonlinear equations in two variables graphically.
    ::以图形方式用两个变量解决两个非线性方程式的系统。

  ---

  播放段落

  Introduction: Lift Off
  ::导言:取消

  

  播放段落

  The Wright brothers used their knowledge of lift force to build the first airplane to take flight.
  ::赖特兄弟利用他们关于增强力的知识 搭建了第一架飞行飞机

  播放段落

  Functions are used to express complicated relationships in a way that can be easily understood and calculated. While this is most commonly used in computer programming, the concept of a function dates back to the origins of C alculus in the 17th century. One example of a function is used in aeronautics to determine the lift force on an object. Lift is the force that allows an object, such as a plane, to accelerate upward. The formula used to determine lift is written below:
  ::函数用于表达复杂的关系,其方式可以容易理解和计算。虽然在计算机编程中最常用,但函数的概念可以追溯到17世纪的微积分起源。一个函数的例子用于航空学,以确定物体的升降力。升降是允许物体(如平面)向上加速的力。用于确定升降的公式如下:

  播放段落

  $$\begin{align*}L = \frac{{C}_{l} \cdot ⍴ \cdot x^2 \cdot s}{2}\end{align*}$$
  ::L=Clx2s2

  播放段落
  • $\begin{align*}L\end{align*}$  is the lift force
    ::L是升降力
  播放段落
  • $\begin{align*}{C}_{l}\end{align*}$   is the coefficient of lift
    ::Cl 是升升系数
  播放段落
  • ⍴ is the air density
    ::是空气密度
  播放段落
  • $\begin{align*}s\end{align*}$  is the wing surface area
    ::s 是翅膀表面面积。
  播放段落
  • $\begin{align*}x\end{align*}$  is the  speed  in meters per second
    ::x 是每秒以米计的速度

  播放段落

  In the early 1900s, Orville and Wilbur Wright used their knowledge of this formula to design the first successful airplane. Their first flight took place on December 17, 1903,  in Kitty Hawk, North Carolina.
  ::19世纪初,Orville和Wilbur Wright利用他们对这个公式的知识设计了第一架成功的飞机。 他们的第一次飞行于1903年12月17日在北卡罗来纳州的Kitty Hawk进行。

  播放段落

  Since then, flight technology has come a long way, but the same formula is still used to calculate lift. T h e  lift, $\begin{align*}L(x),\end{align*}$  during takeoff as a function of speed , $\begin{align*}x,\end{align*}$  can be  calculated for a Boeing 747 given the following information:
  ::从那时起,飞行技术取得了长足进步,但在计算电梯时仍然使用同样的公式。

  播放段落
  • The coefficient of lift, $\begin{align*}{C}_{l},\end{align*}$  is approximately 0.5 during takeoff
    ::升降系数(Cl)在起飞时约为0.5
  播放段落
  • The air density, ⍴, is approximately 1.23  $\begin{align*}\text{kg/m}^3\end{align*}$   at ground level
    ::地面空气密度约1.23千克/立方米。
  播放段落
  • The wing surface area, $\begin{align*}s,\end{align*}$  is 510 $\begin{align*}\text{m}^2\end{align*}$  
    ::翅膀表面面积S,为510平方米

  播放段落

  Substituting these values into the formula will produce the following function:
  ::将这些值替换为公式将产生以下功能:

  播放段落

  $$\begin{align*}L(x) = \frac{0.5 \cdot 1.23 \cdot x^2 \cdot 510}{2} = 156.825x^2\end{align*}$$
  ::L(x) = 0. 5 1. 23x2_ 5102 = 156. 825x2

   

  播放段落

  Discussion Question : What shape do you think the graph will take? Why?
  ::讨论问题:你认为图表会采取什么形状?为什么?

   

  ---

  播放段落

  Activity 1: Plotting Points
  ::活动1:绘图点

  播放段落

  The graph of a function can help understand how the output changes in relation to the input. Although each type of function has its unique characteristics, there is one approach that  can be used to graph any function: plotting points. To graph a function by plotting points, make a list of input-output pairs. This approach is especially helpful when working with an unfamiliar function .
  ::函数的图形可以帮助理解与输入相关的输出变化。 虽然每种函数都有其独特性, 但有一个方法可以用来绘制任何函数的图形: 绘图点。 要用绘图点绘制函数, 请绘制一个输入- 输出对子的列表。 当使用一个不熟悉的函数时, 此方法特别有用 。

  播放段落

  Use this approach to graph  the function in the introduction:  $\begin{align*}L(x) = 156.825x^2.\end{align*}$  Normally, you should start with numbers like -2, -1, 0, 1, 2,... and adjust as needed. However, these values will not give a  complete picture of the function since a plane travels at large positive speeds. To get a  better representation, use the inputs 0, 50, 100, 150, and 200.
  ::使用此方法来绘制导言中的函数 : L( x) = 156. 825x2. 通常, 您应该先从 - 2, - 1, 0, 1, 2... 等数字开始, 然后根据需要进行调整 。 但是, 这些数值不会完整地显示该函数, 因为一个平面以大正速飞行。 要获得更好的表达式, 请使用输入 0, 50, 100, 150 和 200 。

  播放段落
  • $\begin{align*}L(0) = 156.825(0)^2 = 0 \text{ kg} \cdot \text{m/s}^2\end{align*}$  
    ::L(0)=156.825(0)2=0千克=1立方厘米/秒2
  播放段落
  • $\begin{align*}L(50) = 156.825(50)^2 = 392,062.5 \text{ kg} \cdot \text{m/s}^2\end{align*}$  
    ::L(50)=156.825(50)2=392 062.5 kg______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
  播放段落
  • $\begin{align*}L(100) = 156.825(100)^2 = 1,568,250 \text{ kg} \cdot \text{m/s}^2\end{align*}$  
    ::L(100)=156.825(1002=1,568,250公斤=2
  播放段落
  • $\begin{align*}L(150) = 156.825(150)^2 = 3,528,562.5 \text{ kg} \cdot \text{m/s}^2\end{align*}$  
    ::L(150)=156.825(150)2=3,528,562.5公斤=2
  播放段落
  • $\begin{align*}L(200) = 156.875(200)^2 = 6,273,000 \text{ kg} \cdot \text{m/s}^2\end{align*}$  
    ::L(200)=156.8775(200)2=6 273 000 千克/平方米2

  播放段落

  This results in  the following coordinates to graph: 
  ::由此得出以下图表坐标:

  $$\begin{align*}(0,0),~(50,392062.5),~(100,1568250),~(150,3528562.5),~(200,6273000)\end{align*}$$

  播放段落

  Use the interactive below to practice plotting points with other functions. A  curve connecting the points will appear to represent every possible input-output pair for the function .
  ::使用下面的交互功能来用其他函数绘制点。连接点的曲线似乎代表该函数的每一个可能的输入-输出对。

   

  ---

  播放段落

  Activity 2: Graphing Using Technology
  ::活动2:利用技术绘制图表

  播放段落

  Another resource for identifying key features of functions is mathematical graphing software. Graphing  software can be used to visualize functions, identify key features, explore trends, and find input-output pairs. 
  ::用于确定功能主要特征的另一种资源是数学图形化软件,制图软件可用于可视化功能、确定关键特征、探索趋势和寻找投入产出对等。

  播放段落

  Example
  ::示例示例示例示例

  播放段落

  The time it will take for a pendulum to complete one back and forth swing can be found using the following formula: 
  ::使用以下公式可以找到完成一个前后摆动的钟摆所需时间:

  播放段落

  $$\begin{align*}T = 2 \pi \sqrt{\frac{L}{g}}\end{align*}$$
  ::T=2Lg

  播放段落
  • $\begin{align*}T\end{align*}$  is the time it takes for the pendulum to complete one back and forth swing in seconds. T is referred to as the time-period.
    ::T是钟摆在秒内完成一个前后的秋千所需的时间。 T 被称为时段。
  播放段落
  • $\begin{align*}\pi\end{align*}$  is the constant 3.14... 
    ::是常数3.14...
  播放段落
  • $\begin{align*}L\end{align*}$  is the length of the string/pendulum in meters
    ::L 是字符串/支架的长度, 以米计
  播放段落
  • $\begin{align*}g\end{align*}$  is the gravitational constant 9.8  $\begin{align*}\text{m/s}^2\end{align*}$  
    ::g 是引力常数9.8 m/s2

  播放段落

  Graph time-period as a function of pendulum length in the interactive below . T ype in  the equation for a  function and  its graph will appear .  Then use   the interactive to answer the questions that follow.
  ::图形时间段, 以下文互动的周期长度函数为函数。 在公式中键入函数及其图表。 然后使用交互时间段回答下面的问题 。

  播放段落

  $$\begin{align*}T(L) = 2 \cdot 3.14 \sqrt{\frac{L}{9.8}}\end{align*}$$
  ::T(L)=23.14L9.8

   

  播放段落

  Discussion Question : What happens to the time-period as the length of the pendulum increases?
  ::讨论问题:随着钟摆时间的延长,时间期限会怎样?

   

  ---

  播放段落

  Activity 3: Finding Intercepts
  ::活动3:发现拦截

  播放段落

  Mathematical modeling software makes it easy to find the intercepts of complicated equations. The relationships between different functions and their intercepts will be explored throughout Algebra 2 .   Before exploring the intercepts of different types of functions,  you need to know some   key properties of intercepts.  A ll of  the relationships will come from the following definitions.
  ::数学建模软件很容易找到复杂方程式的拦截。 不同功能及其拦截之间的关系将在整个代数2中探索。 在探索不同类型功能的拦截之前, 您需要了解拦截的一些关键属性。 所有的关系都将来自以下定义 。

  播放段落

  $\begin{align*}{y\text{-}}\end{align*}$ intercept
  ::y 界面

  播放段落

  The $\begin{align*}y\text{-}\end{align*}$ intercept of a function is the point where the function crosses the $\begin{align*}y\text{-}\end{align*}$ axis. For this to occur, the input must be 0. Thus the $\begin{align*}y\text{-}\end{align*}$ intercept  will contain the output for $\begin{align*}f(0).\end{align*}$
  ::函数的 Y 界面是函数横跨 y 轴的点。要做到这一点,输入必须是 0。因此y 界面将包含 f(0) 的输出。

  播放段落

  Example
  ::示例示例示例示例

  播放段落

  Previously,  mathematical software was used to find the $\begin{align*}y\text{-}\end{align*}$ intercept of the function  $\begin{align*}T(L) = 2 \cdot 3.14 \sqrt{\tfrac{L}{9.8}}.\end{align*}$   Find  this without graphing the function by calculating $\begin{align*}T(0).\end{align*}$
  ::以前,数学软件用来查找函数T(L)=23.14L9.8的 Y 界面。 在不通过计算 T(0)来绘制函数图的情况下查找此功能。

  播放段落

  $$\begin{align*}T(0) &= 2 \cdot 3.14 \sqrt{\tfrac{0}{9.8}}\\ &= 2 \cdot 3.14 \sqrt{0}\\ &= 2 \cdot 3.14 \cdot 0\\ &= 0\end{align*}$$
  ::T( 0) = 23. 1409.8 = 23. 140 = 23. 140 = 0

  播放段落

  Answer: The $\begin{align*}y\text{-}\end{align*}$ intercept of the function  $\begin{align*}T(L) = 2 \cdot 3.14 \sqrt{\tfrac{L}{9.8}}\end{align*}$   is  (0, 0).
  ::答复:函数T(L)=23.14L9.8的 Y 界面为 0, 0 。

  播放段落

  $\begin{align*}x\text{-}\end{align*}$ intercept
  ::x 拦截

  播放段落

  The $\begin{align*}x\text{-}\end{align*}$ intercept of a function is the point where the function crosses the $\begin{align*}x\text{-}\end{align*}$ axis. For this to occur, the output must be 0. Thus  an   $\begin{align*}x\text{-}\end{align*}$ intercept is  any input for which  $\begin{align*}f(x) = 0.\end{align*}$  Note that a  function  could cross the $\begin{align*}x\text{-}\end{align*}$ axis multiple times. The $\begin{align*}x\text{-}\end{align*}$ intercepts of a function are often referred to as the zeroes .
  ::函数的 x 界面是函数跨过 x 轴的点。 要做到这一点, 输出必须是 0 。 因此, x 界面是 f( x) = 0 的任何输入。 请注意, 函数可以多次跨过 x 轴。 函数的 x 界面通常被称为零 。

  播放段落

  Example
  ::示例示例示例示例

  播放段落

  Jason’s car gets 33 miles per gallon and has a tank that holds 10.6 gallons of gas. After filling his tank, the gas left in his tank, in gallons, as a function of miles traveled is  $\begin{align*}G(m) = 10.6 - \tfrac{1}{33}m.\end{align*}$  What is the $\begin{align*}x\text{-}\end{align*}$ intercept of this function?
  ::杰森的汽车每加仑可达33英里,并有一辆装有10.6加仑汽油的坦克。 装满油箱后,他坦克中的气体,加仑,由于行驶的英里的函数是G(m)=10.6-1133米。 这种功能的X拦截是什么?

  播放段落

  The $\begin{align*}x\text{-}\end{align*}$ intercept of this function can be found by identifying the input, $\begin{align*}m,\end{align*}$  which will produce an output of 0, $\begin{align*}G(m) = 0.\end{align*}$  To find the value of $\begin{align*}m,\end{align*}$   substitute 0 in for $\begin{align*}G(m),\end{align*}$   resulting in the following equation:
  ::此函数的 x 界面可以通过识别输出值为 0, G(m) =0 的输入 m 来找到。 要找到 m 值, 以 G(m) 替代 0 , 得出以下方程:

  播放段落

  $$\begin{align*}0 = 10.6 - \tfrac{1}{33}m\end{align*}$$
  ::0=10.6-133米

  播放段落

  S olve this  algebraically using inverse operations : 
  ::使用反向操作来解析这个代数 :

  播放段落

  $$\begin{align*}0 &= 10.6 - \tfrac{1}{33}m\\ -10.6 & \:-10.6\\ \hline -10.6 &= -\tfrac{1}{33}m\\ \cdot -33 &\:\:\: \cdot -33\\ \hline 349.8 &=m\end{align*}$$
  ::0=10.6-133-10.6-10.6-10.6-10.6-10.6133-33-349.8=m

  播放段落

  Answer: The $\begin{align*}x\text{-}\end{align*}$ intercept is  $\begin{align*}(349.8,0).\end{align*}$
  ::答复: X 拦截为(349.8 0)。

  播放段落

  In this context, the $\begin{align*}x\end{align*}$  represents the number of miles that Jason can drive before he runs out of gas. Use the definitions for intercepts and the interactive below to answer the questions that follow.
  ::在此情况下, x 表示Jason 在用完天然气之前可以驾驶的里程数。 使用拦截的定义和下面的交互作用来回答下面的问题 。

   

  播放段落

  Discussion Question : When is mathematical modeling software more useful when finding intercepts?
  ::讨论问题:在寻找拦截时,数学模型软件何时更有用?

   

  ---

  播放段落

  Activity 4: Finding Intersections
  ::活动4:寻找跨部门

  播放段落

  One function alone can provide valuable information, but sometimes that information can take on increased meaning when compared to another function.
  ::单靠一个功能可以提供宝贵的信息,但有时,与另一个功能相比,这些信息具有更大的意义。

  播放段落

  T he introduction  discussed how to calculate  lift, but lift alone lacks meaning. By comparing  lift  to the object's force of gravity (or weight),  you can determine whether or not the object will fly:
  ::引言讨论了如何计算升,但单是升就缺乏意义。通过比较升到物体的重力(或重量),您可以确定该物体是否会飞:

  播放段落
  • If lift > weight, the object will accelerate upward.
    ::如果升升 > 重量,该对象会向上加速。
  播放段落
  • If lift = weight, the object will hover.
    ::如果升起=重量,该物体将徘徊。
  播放段落
  • If lift < weight, the object will fall to the ground.
    ::如果升起 < 重量, 物体将落地 。

  播放段落

  Compare  lift as a function of  speed for a Boeing 737,  $\begin{align*}L(x) = 156.825x^2,\end{align*}$  with the function  for  its weight to determine the speed required for a Boeing 737 to take off from a runway. Since the weight of a Boeing 737 does not depend on its speed , the function for weight will be a constant function. Weight is determined using the following formula:
  ::将升降作为波音 737, L(x) = 156. 825x2 的速度函数, 其重量函数确定波音 737 从跑道起飞所需的速度。 由于波音 737 的重量不取决于其速度, 重量函数将是一个不变的函数。 重量函数使用以下公式确定 :

  播放段落

  $$\begin{align*}W = g \cdot m\end{align*}$$
  ::W=gm

  播放段落
  • $\begin{align*}W\end{align*}$  is the weight of the object in  $\begin{align*} \text{kg} \cdot \text{m/s}^2\end{align*}$  
    ::W 是物体的重量, 单位: kgm/s2
  播放段落
  • $\begin{align*}g\end{align*}$  is the gravitational constant  $\begin{align*}9.8 \text{ m/s}^2\end{align*}$  
    ::g 是引力常数9.8 m/s2
  播放段落
  • $\begin{align*}m\end{align*}$  is the mass in kg
    ::m 是以千克为单位的质量。

  播放段落

  A  Boeing 737 weighs approximately 80,000 kg,  so weight as a function of  speed  is : 
  ::波音737飞机的重量约为80 000公斤,按速度计算重量如下:

  播放段落

  $$\begin{align*}W(x) = 9.8 \cdot 80,000 = 784,000\end{align*}$$
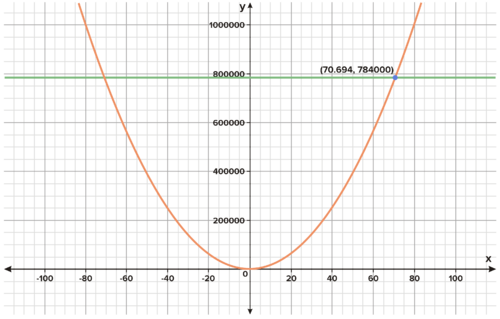
  ::W(x)=9.88080=784 000

  播放段落

  T he  speed required for takeoff is the  speed   at which lift is equal to weight − i n other words, the point where  $\begin{align*}L(x) = W(x).\end{align*}$  This is where the graphs of the functions $\begin{align*}L(x)\end{align*}$  and $\begin{align*}W(x)\end{align*}$  intersect, as shown below: 
  ::起飞所需的速度是升起速度等于重量的速度,换句话说,就是L(x)=W(x)的点。这是函数L(x)和W(x)相交之处的图形,如下文所示:

  

  播放段落

  At a   speed of approximately 70 m/s, the plane will have a lift equal to its weight. The  speed 70 m/s translates to 156.6 mi/hr or 252 km/hr. The plane will accelerate upward from the runway (fly) at a speed greater than 70 m/s.
  ::速度大约为70米/秒,飞机的升降速度相当于其重量,速度70米/秒等于156.6米/小时或252公里/小时,飞机从跑道(飞行)向上加速速度超过70米/秒。

  播放段落

  Use the same approach to determine the  speed that the Wright brothers needed to fly their first plane, given the following information:
  ::使用同样的方法来确定Wright兄弟们飞行第一架飞机所需的速度,考虑到以下信息:

  播放段落
  • $\begin{align*}{C}_{l},\end{align*}$  the coefficient of lift, is 0.5
    ::Cl,升升系数是0.5
  播放段落
  • ⍴, the air density, is 1.23  $\begin{align*}\text{kg/m}^3\end{align*}$  at ground level
    ::空气密度为1.23千克/立方米,地面为1.23千克/立方米。
  播放段落
  • $\begin{align*}s,\end{align*}$  the wing surface area, is 47.4  $\begin{align*}\text{m}^2\end{align*}$  
    ::s, 翼表面积为47.4平方米。
  播放段落
  • $\begin{align*}g,\end{align*}$  the gravitational constant, is 9.8  $\begin{align*}\text{m/s}^2\end{align*}$  
    ::g,引力常数为9.8米/秒2
  播放段落
  • $\begin{align*}m,\end{align*}$  the mass, is 274 kg
    ::m, 质量, 274公斤

   

  播放段落

  Discussion Question : The speed needed for the Wright brother's plane takeoff translates to approximately 30 miles per hour. Although the Wright brothers’ plane had an engine, it was only 7 horsepower. For comparison, a standard modern car has about 120 horsepower. The Wright brothers plane wasn’t capable of getting to 30 miles per hour   using the motor alone.  What  could they have used to  reach  that speed?
  ::讨论问题:Wright兄弟的飞机起飞速度相当于每小时大约30英里。 尽管Wright兄弟的飞机有引擎,但只有7匹马力。 相比之下,标准的现代汽车有120匹马力。 Wright兄弟的飞机无法单用发动机达到每小时30英里。 他们用什么方法达到这个速度?

   

  ---

  播放段落

  Activity 5: Solving Equations Using Technology
  ::活动5:利用技术解决等式

  播放段落

  As  seen in the previous activity, the intersection of two functions can be found using technology.  In order to find when the function  $\begin{align*}W(x) = 784,000\end{align*}$  wa s equal to the function  $\begin{align*}L(x) = 156.825x^2,\end{align*}$   the $\begin{align*}x\text{-}\end{align*}$ value at the point of intersection on a graph was needed.  T hese two functions can be thought of as a system of equations , and another approach to solving a system of equations is  by using  substitution.
  ::如前一活动所示,两个函数的交叉点可以使用技术找到。为了找到 W(x)=784,000 函数何时等于函数 L(x)=156.825x2, 需要图形中交叉点的 x 值。这两个函数可以被视为一个方程系统,而解决一个方程系统的另一种方法是使用替代。

  播放段落

  Similarly, g raphing can be used to  solve equations. E ach side of an equation can be thought of as  a  function . T he intersection of the functions will represent the solution to the equation.
  ::同样,图形化也可以用来解析方程式。方程式的每个侧面都可以被视为函数。函数的交叉点将代表方程式的解决方案。

  播放段落

  The  equation in the example below may be too complicated to solve by hand (Although it will be covered in Solving Rational Equations). Instead, use  graphing software to find the answer.  Write each side of the equation as a function and find the intersection. The $\begin{align*}x\text{-}\end{align*}$ coordinate  of the  intersection point  will represent the solution to the equation and the $\begin{align*}y\text{-}\end{align*}$ coordinate will represent the value that both sides of the equation  will  equal.  Note that some equations may have more than one answer.
  ::以下示例中的方程式可能太复杂,无法用手解答(尽管它将在逻辑方程式中包含 ) 。 相反, 使用图形化软件来找到答案。 将方程式的每侧写成函数并找到交叉点。 交叉点的 x 坐标将代表方程式的解决方案, Y 坐标将代表方程式两侧的等值。 注意某些方程式可能有多个答案 。

  播放段落

  Example
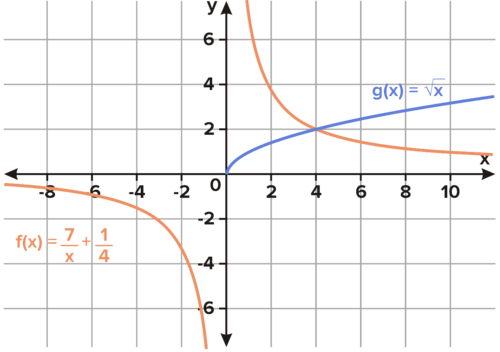
  ::示例示例示例示例

  播放段落

  Solve the equation by graphing: 

  $$\begin{align*}\frac{7}{x} + \frac{1}{4} = \sqrt{x}\end{align*}$$
  ::通过图形化解决方程式: 7x+14x

  播放段落

  B egin by writing  each side of the equation as a function: 
  ::开始将方程式的每侧写成函数 :

  播放段落

  $$\begin{align*}f(x) &= \frac{7}{x} + \frac{1}{4} \\ g(x)&=\sqrt{x}\end{align*}$$
  :x) = 7x+14g(x) x

  播放段落

  Next, graph the functions.
  ::下一位, 绘制函数图 。

  

  播放段落

  The point of intersection is (4, 2). The solution to the equation is the $\begin{align*}x\text{-}\end{align*}$ coordinate .
  ::交叉点是(4,2),方程的解决方案是x坐标。

  播放段落

  Answer: $\begin{align*}x = 4\end{align*}$
  ::答复:x=4

  播放段落

  V erify this by substituting 4 into the equation.
  ::用方程中的4个替换来验证这一点 。

  播放段落

  $$\begin{align*}\frac{7}{x} + \frac{1}{4} &= \sqrt{x}\\\\ \frac{7}{4} + \frac{1}{4} &= \sqrt{4}\\\\ \frac{8}{4} &= \sqrt{4}\\\\ 2 &= \sqrt{4}\\\\ 2 &= 2 \quad \checkmark\end{align*}$$
  ::7x+14x74+144844242=2

  播放段落

  Use this strategy and the interactive below to  answer the questions that follow. 
  ::使用本战略和下文互动方式回答以下问题。

   

   

  ---

  播放段落

  Wrap-Up: Review Questions
  ::总结:审查问题

  播放段落

  Summary
  ::摘要

  播放段落
  • There are several ways to graph functions: plotting pairs of points, finding intercepts, or using technology.
    ::图表功能有几种方法:绘制对点图、寻找拦截或使用技术。
  播放段落
  • A  point of intersection for two functions is   where their graphs meet.  Given two functions, $\begin{align*}f(x)\end{align*}$  and $\begin{align*}g(x),\end{align*}$  the point of intersection can be thought of as  the solution to the equation $\begin{align*}f(x)=g(x).\end{align*}$  
    ::两个函数的交叉点是其图形相交之处。如果使用两个函数 f(x) 和 g(x) , 交叉点可被视为公式 f(x) = g(x) 的解决方案 。