2.6 反反函数-interactive

章节大纲

• 选择节常规

  折叠 展开

  常规

  全部折叠 展开全部

  • 选择活动新闻通告

    

    新闻通告 讨论区
• 选择节反反函数

  折叠 展开

  反反函数

  播放段落

  Learning Objectives
  ::学习目标

  播放段落
  • Read the values of an inverse function from a graph.
    ::从图表中读取反函数的值。
  播放段落
  • Find the inverse of a function given a set of points.
    ::查找函数的反向,给定一组点。
  播放段落
  • Verify by composition that one function is the inverse of another.
    ::以组成来核查一个函数是另一个函数的反函数。
  播放段落
  • Find the inverse of a function given an equation.
    ::查找给定方程式的函数的反向 。
  播放段落
  • Find where a function and its inverse intersect.
    ::查找函数及其反相交点的位置。

  ---

  播放段落

  Introduction: Reversing  a Function
  ::导言:职能的逆转

  

  播放段落

  Thus far, you have  seen many examples of  the uses of functions in computer programming. However, situations like the following require the use of inverse functions.
  ::到目前为止,你已经看到许多在计算机编程中使用功能的例子,但是,下列情况需要使用反向功能。

  播放段落

  Donna is a programmer writing an app that will report weather information. See the interactive below for an example of how Donna's app will work.
  ::Donna 是一个程序程序员, 正在撰写一个程序, 它将报告天气信息。 请参看下面的交互功能, 以实例说明 Donna 的应用程序将如何运作 。

  播放段落

  Donna wrote the following function 
  ::Donna 写了以下函数

  播放段落

  function toCelsius(t) {
  ::函数到 Cellius(t) {

  播放段落

  return 5(t - 32)/9
  ::返回 5(t - 32)/9

  }

  播放段落

  In math, this translates to  $\begin{align*}C(t) = \frac{5}{9}(t-32).\end{align*}$  For Donna's app to work, she needs to be able to convert between Fahrenheit and Celsius. She needs to write a function that will take her from Celsius back to Fahrenheit. Use the interactive below to  access the code  and write a function toFahrenheit(t) that will convert a temperature from Celsius to Fahrenheit . 
  ::在数学中, 这翻译为 C( t) = 59 ( t-32. ) 。 唐娜的应用程序要工作, 她需要能够转换 Fahrenheit 和 colent 。 她需要写一个函数, 将她从摄氏度带回 Fahrenheit 。 使用下面的交互功能访问代码, 并将一个函数写给 Fahrenheit ( t) , 该函数将把温度从摄氏度转换到 Fahrenheit 。

  播放段落

  The function   $\begin{align*}C(x)\end{align*}$   converts a temperature from Fahrenheit to Celsius and the function $\begin{align*}F(x)\end{align*}$   converts a temperature from Celsius to Fahrenheit. Use this information to answer the questions below.
  ::函数C(x) 将温度从法赫伦海特转换为摄氏度,而函数F(x) 将温度从摄氏度转换为法赫伦海特。使用此信息回答下面的问题。

  ---

  播放段落

  Activity 1:  Understanding  Inverses of Functions
  ::活动1:了解职能的反面

  播放段落

  The interactive below displays the graphs of $\begin{align*}C(t)\end{align*}$  and $\begin{align*}F(t).\end{align*}$  What do you notice about the graphs of the two functions?
  ::以下互动显示 C(t) 和 F(t) 的图形。 您注意到两个函数的图形是什么吗 ?

  播放段落

  In the section Functions, f unctions were introduced as rules that take inputs and produce outputs.
  ::在“职能”一节中,引入了作为吸收投入和产出的规则的职能。

  播放段落

  Example
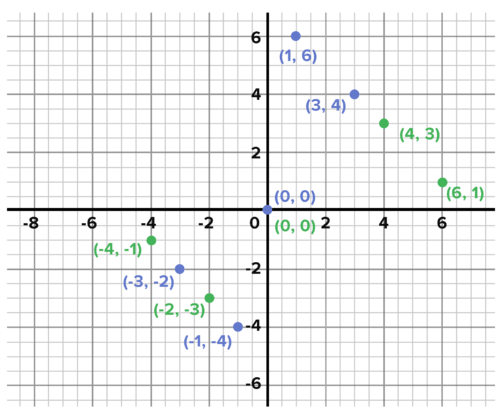
  ::示例示例示例示例

  播放段落

  A function  $\begin{align*}h(x)\end{align*}$   is defined by the coordinates  $\begin{align*}\{(-3, -2), (-1,-4), (0,0), (1,6), (3,4)\},\end{align*}$ find and graph the inverse of this function.
  ::函数 h(x) 由 {(- 3) 3, 2, (1- 1) -4, (0) , (1) 6, (3, 4)} 坐标定义, 查找并绘制此函数的反方向 。

  播放段落

  T he inputs and their corresponding outputs are given. For example, it is given that  $\begin{align*}h(-1)=-4.\end{align*}$   T he coordinates of the inverse function by reversing the $\begin{align*}x\text{-}\end{align*}$ value and the $\begin{align*}y\text{-}\end{align*}$ value.
  ::给出了投入及其相应的产出。例如,给出了 h(-1) @%4。通过反转 x 值和 y 值来显示反函数的坐标 。

  播放段落

  Answer:   $\begin{align*}\{(-2,-3), (-4,-1), (0,0), (6,1), (4,3)\}\end{align*}$  
  ::答复:{(-2)-3,(-4)-1,(0),(6),(1),(4),(3)}

  

  播放段落

  The graph of an inverse function is the reflection of the graph of the function over the line  $\begin{align*}y = x.\end{align*}$   T he graph of an inverse function can be found by plotting the points of a function and reversing the $\begin{align*}x\end{align*}$  and $\begin{align*}y\text{-}\end{align*}$ values.
  ::反向函数的图形是 y=x 线上的函数图形的反射。反向函数的图形可以通过绘制函数的点和反转 x 和 y 值来找到。

  播放段落

  Discussion Question : How do you think the domain of an inverse could relate to the range of the original function.
  ::讨论问题:你如何看待反向的域与原有功能的范围有关。

  ---

  播放段落

  Extension: Distances Between Inverse Values
  ::扩展名: 反向值之间的距离

  播放段落

  Answer the questions below to find  the distance between a function  value and its corresponding inverse value.
  ::回答下面的问题,以找到函数值与其对应反向值之间的距离。

  ---

  播放段落

  Activity 2:  Checking Inverse Functions
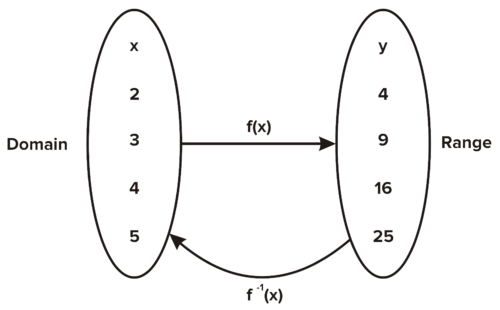
  ::活动2:检查反向函数

  播放段落

  A function is written as  $\begin{align*}f(x)\end{align*}$  and its inverse is written as  $\begin{align*}f^{-1}(x).\end{align*}$  A common misconception is to see the -1, interpret it as an exponent, and write  $\begin{align*}\frac{1}{f(x)},\end{align*}$  but this is not correct. Instead,  $\begin{align*}f^{-1}(x)\end{align*}$  should be viewed as a new function from the range of  $\begin{align*}f(x)\end{align*}$  back to the domain. T he relationship between the function  $\begin{align*}f(x) = x^2\end{align*}$  and its inverse can be seen below for the domain that is equal to or greater than 0.
  ::函数以 f( x) 写成, 其反义写成 f- 1( x) 。 一个常见的误解是看到 -1, 将它解释为引言, 并写 1f( x) , 但这是不正确的。 相反, f- 1( x) 应被视为从 f( x) 返回到域域的一个新函数。 函数 f( x) =x2 与其反义之间的关系可以在下面的等于或大于 0 的域中看到 。

  

  播放段落

  It is important to see the cycle that starts with $\begin{align*}x,\end{align*}$  becomes  $\begin{align*}y,\end{align*}$  and  then goes back to $\begin{align*}x.\end{align*}$  For two functions to truly be inverses of each other, this cycle must hold algebraically. 
  ::重要的是要看到以 x 开始的周期, 变成 y, 然后又回到 x。 两个函数要真正相互反转, 这个周期必须保持代数 。

  播放段落

  $$\begin{align*}f(f^{-1} (x) )=x \:\:\text{ and }\:\: f^{-1} (f(x) )=x\end{align*}$$
  ::f( f- 1 (x)) =x 和 f- 1 (f(x)) =x

  播放段落

  The statement $\begin{align*}f^{-1} (f(x) )=x\end{align*}$  means  that putting a value into  $\begin{align*}f(x)\end{align*}$  and then putting the output from  $\begin{align*}f(x)\end{align*}$  into  $\begin{align*}f^{-1}(x)\end{align*}$  will  produce  the original input value. Since this is true for all inputs, all possible inputs will be represented with $\begin{align*}x.\end{align*}$  This is the mathematical way of stating the definition describ ed throughout this section.
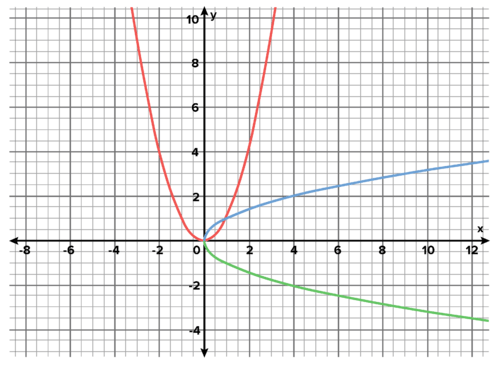
  ::语句 f- 1 (f(x) =x 表示将一个值输入 f(x) ,然后将 f(x) 输出输入到 f- 1 (x) 将产生原始输入值。由于所有输入都是如此,所有可能的输入都将以 x 表示。这是本节所描述定义的数学表达方式。

  播放段落

  The converse of this relationship,  $\begin{align*}f(f^{-1} (x) )=x,\end{align*}$  is true as well.  For example,  $\begin{align*}f(x)={x}^{2}\end{align*}$  and  $\begin{align*}f^{-1}(x)=\sqrt{x}\end{align*}$  are inverse s , and both  $\begin{align*}\left(\sqrt{4}\right)^{2}=4\end{align*}$  and  $\begin{align*}\sqrt{\left({4}^{2}\right)}=4\end{align*}$ .  However, the $\begin{align*}x\end{align*}$ -values above are all positive numbers.  A function and its inverse must hold true algebraically for all real numbers, including both positive and negative numbers. If  $\begin{align*}f(x)={x}^{2}\end{align*}$  and  $\begin{align*}x=\text{-}2\end{align*}$ , then $\begin{align*}f(\text{-}2)=4.\end{align*}$  However,  following the pattern above,  $\begin{align*}{f}^{-1}(4)=2\end{align*}$ , and not  $\begin{align*}\text{-}2.\end{align*}$  On a graph, this would look like the following:
  ::此关系的正对等值 f( f) -1 (x) =x, 也是正确的。 例如, f( x) =x2 和 f- 1 (x) =x =x 是反数, 两者( {4) 2= 4 和 {( 42) = 4) 。 但是, 以上 x 值都是正数。 一个函数及其反数必须对所有实际数字, 包括正数和负数都保持正正正数和负数的正代数。 如果 f( x) =x2 和 x=2, 那么f( 2) = = 4 。 但是, 按照上述模式, f- 1 (4) =2 而不是 - 2 。 图表上, 这看起来像如下 :

  

  播放段落

  We can see that  $\begin{align*}y=x^2\end{align*}$   reflects over the line  $\begin{align*}y=x\end{align*}$  but the result is not a function.  This  means that   $\begin{align*}f(x)={x}^{2}\end{align*}$   is not invertible.  
  ::我们可以看到 Y=x2 反射在 y=x 线上, 但结果不是一个函数。 这意味着 f( x) =x2 不是不可倒省的 。

  播放段落

  Example
  ::示例示例示例示例

  播放段落

  Verify that the inverse of $\begin{align*}f(x) = 4x - 1 \text{ is } f^{-1}(x) = \frac{x+1}{4}\end{align*}$  algebraically. In other words, verify that  $\begin{align*}f^{-1} (f(x) )=x \text{ and }f(f^{-1} (x) ) = x.\end{align*}$
  ::校验 f( x) = 4x- 1 的反义为 f-1( x) = x+14 代数。 换句话说, 校验 f-1( f( x)) =x 和 f( f- 1 (x)) =x 。

  播放段落

  To verify inverse functions algebraically,  it  must be shown that  $\begin{align*}f^{-1} (f(x) )=x \text{ and }f(f^{-1} (x) ) = x.\end{align*}$ The first step is to evaluate the function $\begin{align*}f ^{-1}\big( f(x) \big):\end{align*}$
  ::要校验反函数代数,必须显示 f-1(f(x))=x 和 f(f-1(x))=x。 第一步是评价函数 f-1(f(x) :

  播放段落

  $$\begin{align*}f^{-1} \big( f(x) \big) & = f^{-1}(4x-1) \\\\ & =\frac{(4x-1) + 1}{4}\\\\ &=\frac{4x}{4}\\\\ &=x\end{align*}$$
  ::f- 1 (f(x)) = f- 1 (4x- 1) = (4x- 1) +14= 4x4=x

  播放段落

  We will also verify  $\begin{align*}f \big( f^{-1}(x) \big):\end{align*}$  
  ::我们还将核查f(f-1(x)):

  播放段落

  f ( f − 1 ( x ) ) = f ( x + 1 4 ) = 4 ( x + 1 4 ) − 1 = 4 ( x + 1 4 ) − 1 = x + 1 − 1 = x

  $$\begin{align*}f(f^{-1} (x) ) &= f\left(\frac{x+1}{4}\right)\\\\ &=4\left( \frac{x+1}{4}\right)-1\\\\ &=\cancel{4}\left( \frac{x+1}{\cancel{4}}\right)-1\\\\ &=x+1-1\\\\ &=x \end{align*}$$  
  ::f( f- 1 (x)) = f( x+14) = 4( x+14) - 1= 4( x+14) - 1= 4( x+14) - 1= 4( x+14) - 1= X

  播放段落

  Answer: The two functions are inverses because they each "undo" the other, leaving the original $\begin{align*}x.\end{align*}$    
  ::回答:这两个函数是反的,因为它们彼此“不做”,留下原来的x。

  播放段落

  The example above  verifies that no matter what value  is substituted into  $\begin{align*}f(x),\end{align*}$  substituting the output into  $\begin{align*}f^{-1}(x)\end{align*}$  will produce the original input. T he converse was proven true as well by checking  $\begin{align*}f^{-1} \big( f(x) \big).\end{align*}$  Later in the Algebra 2, examples  will be provided where  $\begin{align*}f^{-1} \big( f(x) \big) \end{align*}$  is true but  $\begin{align*}f \big( f^{-1}(x) \big)\end{align*}$  is not. 
  ::上述例子证实,无论将什么值替换为 f(x),将输出替换为 f-1(x) 将产生原始输入。 反之,通过检查 f-1(f(x) ) 来证明。 后期的代数 2 将提供 f-1(f(x)) 真实但 f(f)-1(x) 不真实的例子。

  播放段落

  Answer the questions  below to practice verifying inverse functions.
  ::回答下列问题,以实践核查反向功能。

  播放段落

  Discussion Question : What is the inverse of the absolute value function $\begin{align*}y = |x|\end{align*}$ ?
  ::讨论问题:绝对值函数yx的反差是什么?

  ---

  播放段落

  Activity 3: Finding Inverse Functions
  ::活动3:查找反向函数

  播放段落

  When given a function, there are two steps required to find the inverse function.
  ::当给定函数时,需要两个步骤才能找到反向函数。

  播放段落
  1. Switch the variables $\begin{align*}x\end{align*}$  and   $\begin{align*}y.\end{align*}$  
     ::切换变量 x 和 Y。
  播放段落
  2. S olve the function for   $\begin{align*}y.\end{align*}$  
     ::解决y 的函数 。

  播放段落

  Keep in mind that to find the coordinates  of the inverse function were found by  switching the $\begin{align*}x\end{align*}$  and $\begin{align*}y\end{align*}$  coordinates. T o find the inverse of an equation or function, switch the $\begin{align*}x\end{align*}$  and $\begin{align*}y\end{align*}$  variables which will have the effect of switching  all  coordinates.  After finding the inverse, it is important to check both directions of compositions to make sure that together the function and the inverse produce the value   $\begin{align*}x.\end{align*}$  In other words, verify that   $\begin{align*}f(f^{-1} (x) )=x\end{align*}$  and   $\begin{align*}f^{-1} (f(x) )=x\end{align*}$ .
  ::请注意,要找到反函数的坐标,请切换 x 和 y 坐标。要找到方程式或函数的反方向,请切换具有切换所有坐标效果的 x 和 y 变量。在查找反方向后,必须检查组合的两种方向,以确保函数和反方向一起产生值 x。换句话说,验证 f(f)-1(x)=x 和 f-1(f(x))=x 。

  播放段落

  Example
  ::示例示例示例示例

  播放段落

  F ind the inverse of  $\begin{align*}y=2x^3.\end{align*}$
  ::查找 y=2x3 的反义。

  播放段落

  1. Switch the variables $\begin{align*}x\end{align*}$   and $\begin{align*}y.\end{align*}$
  ::1. 转换变量x和y。

  播放段落

  $$\begin{align*}y&=2x^3\\ x&=2y^3\end{align*}$$
  ::y= 2x3x= 2y3 y3

  播放段落

  Recall that $\begin{align*}y\end{align*}$  can be used to represent $\begin{align*}f(x)\end{align*}$  in a function. When finding an inverse function, you may want to first replace $\begin{align*}f(x)\end{align*}$  with $\begin{align*}y.\end{align*}$
  ::回想到 y 可用于在函数中代表 f(x) 。在查找反函数时,您可能要先用 y 替换 f(x) 。

  播放段落

  2. Solve the function for $\begin{align*}y.\end{align*}$
  ::2. 解决y的函数。

  播放段落

  $$\begin{align*}x&=2y^3\\\\ \frac{x}{2}&=y^3\\\\ \sqrt[3]{\frac{x}{2}}&=y\end{align*}$$
  ::x=2y3x2=y33x2=y

  播放段落

  Finally, check to make sure that  $\begin{align*}f(f^{-1} (x) )=x \text{ and } f^{-1}(f (x) )=x.\end{align*}$
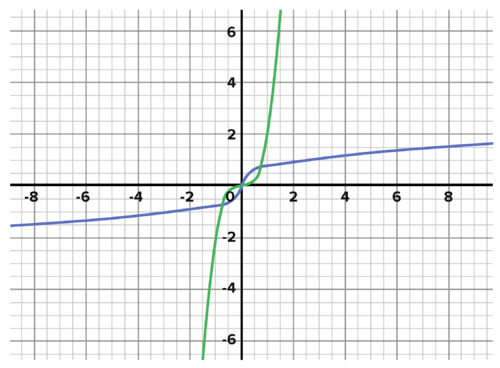
  ::最后,检查以确保 f( f- 1 (x)) =x 和 f- 1 (f (x) =x。

  $$\begin{align*}y&=2(\sqrt[3]{\frac{x}{2}})^3\\\\ y&=2(\sqrt[\cancel{3}]{\frac{x}{2}})^{\cancel{3}}\\\\ y &= \frac{\cancel{2}x}{\cancel{2}}\\\\ y &= x\end{align*}$$

  $$\begin{align*}y&=\sqrt[3]{\frac{(2x^3)}{2}}\\\\ y&=\sqrt[3]{\frac{(\cancel{2}x^3)}{\cancel{2}}}\\\\ y&=\sqrt[3]{x^3}\\\\ y &= x\end{align*}$$

  播放段落

  Inverse functions can also be verified graphically.
  ::反向函数也可以用图形方式校验 。

  

  播放段落

  Answer:  The inverse of  $\begin{align*}y=2x^3 \text{ is } y=\sqrt[3]{\frac{x}{2}}.\end{align*}$  
  ::答复:y=2x3的反数是y=3x2。

  播放段落

  We can write this in function notation as $\begin{align*}f^{-1}(x)=\sqrt[3]{\frac{x}{2}}.\end{align*}$
  ::我们可以将此写为 f- 1 (x) = 3x2 的函数符号 。

  播放段落

  Answer the questions  below to practice .
  ::回答以下实践问题。

  播放段落

  Discussion Question : What would the inverse of a piecewise function look like both graphically and algebraically? 
  ::讨论问题:一个片段函数的反面在图形和代数两方面都看起来像什么?

  

  播放段落

  Extension Discussion Question :   T he step function $\begin{align*}y = ||x||\end{align*}$  is referred to as the floor function in computer programming. What would the inverse of the floor function look like both graphically and algebraically?
  ::扩展讨论 问题: 阶梯函数 yx 被称为计算机编程中的底部函数 。 底部函数的反面像图形和代数吗 ?

  ---

  播放段落

  Extension: Inverse Functions Practice
  ::扩展名: 反函数练习

  播放段落

  Use the interactive below for additional practice finding inverse functions.
  ::使用下面的交互功能查找反函数的额外做法。

  播放段落

  Discussion Question : What would happen if you plugged a number into a function, found its output value, and then plugged the output value into the inverse function? 
  ::讨论问题:如果将数字插入函数,发现其输出值,然后将输出值插入反函数,会发生什么情况?

    

  ---

  播放段落

  Wrap-Up: Review Questions
  ::总结:审查问题

  播放段落

  The video below explores  functions and their inverses.
  ::以下影片探讨功能及其反射。

  播放段落

     Summary
  ::摘要

  播放段落
  • An inverse function switches the output and input of a function.
    ::反向函数切换函数的输出和输入。
  播放段落
  • When finding the inverse of a function  switch the $\begin{align*}x\end{align*}$  and $\begin{align*}y\end{align*}$  then solve for $\begin{align*}y.\end{align*}$  
    ::当找到函数的反转时, xandy 切换 xandy 然后为 y 解决 。
  播放段落
  • To check if two functions are inverses, find $\begin{align*}f^{-1}(f(x))\end{align*}$  and  $\begin{align*}f(f^{-1}(x))\end{align*}$  if they both equal $\begin{align*}x\end{align*}$  then the functions are inverses of each other. 
    ::要检查两个函数是否反向, 请查找 f- 1(f(x)) 和 f(f- 1(x)) , 如果这两个函数都等于 x, 那么函数是反向的 。
  播放段落
  • Remember, $\begin{align*}f^{-1}(x)\not=\frac{1}{f(x)}\end{align*}$  
    ::记住, f- 1( x) 1f( x)